стр.19-26

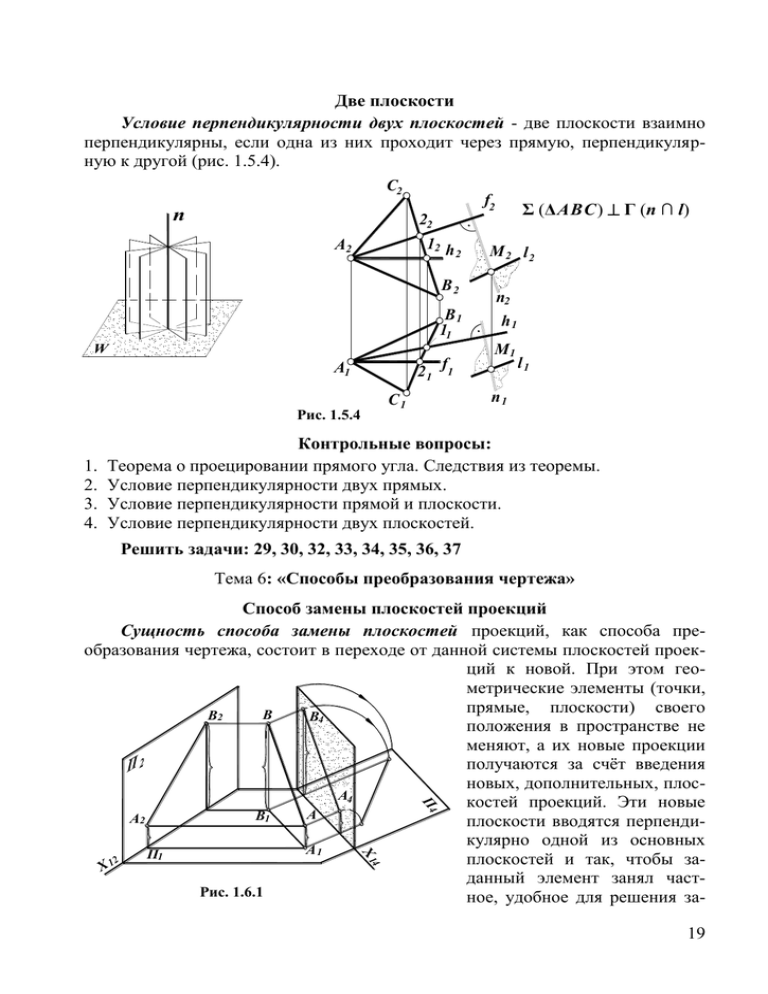
Две плоскости
Условие перпендикулярности двух плоскостей - две плоскости взаимно
перпендикулярны, если одна из них проходит через прямую, перпендикулярную к другой (рис. 1.5.4).
C2
f2
Σ (ΔABC)  Γ (n ∩ l)
n
22
12 h
A2
M 2 l2
2
B2
B1
11
W
2 1 f1
A1
1.
2.
3.
4.
h1
M1
l1
n1
C1
Рис. 1.5.4
n2
Контрольные вопросы:
Теорема о проецировании прямого угла. Следствия из теоремы.
Условие перпендикулярности двух прямых.
Условие перпендикулярности прямой и плоскости.
Условие перпендикулярности двух плоскостей.
Решить задачи: 29, 30, 32, 33, 34, 35, 36, 37
Тема 6: «Способы преобразования чертежа»
П4
Способ замены плоскостей проекций
Сущность способа замены плоскостей проекций, как способа преобразования чертежа, состоит в переходе от данной системы плоскостей проекций к новой. При этом геометрические элементы (точки,
прямые, плоскости) своего
B
B2
B4
положения в пространстве не
меняют, а их новые проекции
получаются за счёт введения
новых, дополнительных, плосA4
костей проекций. Эти новые
A
B
1
A2
плоскости вводятся перпендикулярно одной из основных
A1
П1
2
плоскостей и так, чтобы заX1
данный элемент занял частРис. 1.6.1
ное, удобное для решения за4
X1
19
дач положение. Тогда проекции элементов на новой плоскости проекций строятся с измерением координат точек с заменяемой плоскости проекций (рис.
1.6.1)
Способ вращения
Сущность способа вращения, как способа преобразования чертежа, состоит в том, что основные плоскости проекций в пространстве своего положения не меняют, а геометрические элементы (точки, прямые, плоскости) вращают (перемещают) до тех пор, пока они не займут частное, удобное для решения задач положение.
При вращении геометрические элементы, например точка А, перемещаются вокруг оси вращения i и описывают
окружность с центром О и радиусом R, лежащую в плоскости вращения , перi
пендикулярной оси вращения
(рис. 1.6.2)
В качестве осей вращения обычно приниR A
мают прямые частного положения (проецируO
ющие или уровня), так как при общем положении оси основные элементы (ось, центр, радиус и плоскость вращения) на проекционном
чертеже строить весьма затруднительно.
Рис.1.6.2
Решение всех метрических задач способами преобразования чертежа сводится к четырём основным метрическим задачам (табл. 1.5.1).
20
Таблица 1.5.1
Решение основных метрических задач
Заменой плоскостей проекций
A2
B2
х12
i2  B2  O2  B2
A1
B1
х 14
Вращением вокруг проецирующей оси
B1  O1  B1
B4
A1
O1
A
A11
A4
W1
i1
i2
A2
h2 B2
A2
A2
A
2
х12
B2  A2  A2
h2
h1
B1
н.в.
A1
h1
A1
j2
 2 (B)
B2
x12
 2(C)
C2
x14
B1
B4
11 h1
A1
h1
B2 B2
12  A2
12 h2
A2
н.в. A
1
B1 B1  O1  i1
A4  B4  h4
х14
4. Преобразование проецирую- 3. Преобразование плоскости о.п. 2. Преобразование пря- 1. 1.Преобразование
щей плоскости в плоскость
в проецирующую плоскость
мой уровня в проеципрямой о.п. в прямую
уровня
рующую прямую
уровня
О.М.З.
C1
12
C2
C2
B1
A1  A1  j1
11
A4 14 h4
C1
B1
C4
C1
11
2
A2
C2
х12
х 14
H.В.
A4
B4
B2
A1  A1
C1
C4
B1
A1
C2
C1
A2  j2  O2
B2
H.В.
B1
j B
C2
1
C1
1
1
21
Контрольные вопросы:
1. В чем сущность преобразования проекций способом замены плоскостей?
2. Назовите задачи, для решения которых достаточно заменить только одну
плоскость проекций.
3. Назовите задачи, которые решаются заменой двух плоскостей проекций.
4. В чем сущность преобразования проекций способом вращения оригинала
вокруг проецирующей оси?
5. Назовите пять элементов вращения точки вокруг оси.
6. Назовите задачи, которые выполняются одним вращением и двумя.
Решить задачи: 38, 39, 40, 41, 42, 44, 45, 46, 47
Тема 7: «Многогранники»
Виды многогранников
Многогранником называется замкнутая пространственная фигура, ограниченная плоскими многоугольниками.
Отсеки плоскостей, ограничивающие поверхность, называются гранями,
линии их пересечения – рёбрами, а точки пересечения рёбер – вершинами многогранника.
На комплексном чертеже многогранная поверхность полностью определяется
заданием её рёбер и вершин.
Пирамида - многогранник, в основании которого лежит многоугольник
(с
числом сторон не менее трёх), а боковыми
гранями являются треугольники с общей
вершиной (рис. 1.7.1). Если в основании
лежит правильный многоугольник, а высота перпендикулярна основанию, пираРис. 1.7.1
мида называется правильной.
В зависимости от угла, образованного высотой с основанием, пирамида
может быть прямой или наклонной.
Призма – многогранник, две грани которого (основания) – равные многоугольники, а боковые грани – параллелограммы
с параллельными и равными по величине
рёбрами (рис. 1.7.2).
В зависимости от угла, образованного
рёбрами с основанием, призма может быть
прямой или наклонной.
Если в основании призмы – прямоугольник, то её называют параллелепипеРис. 1.7 2
дом.
22
Пересечение многогранников плоскостью
При пересечении многогранников (призмы, пирамиды) плоскостью в сечении получается плоская фигура, ограниченная линиями пересечения секущей
плоскости с гранями многогранника (рис.1.7.3 )
Пересечение многогранников прямой
Построение точек пересечения прямой с поверхностью многогранника
(призмой, пирамидой) сводится к построению линии пересечения многогранника с проецирующей плоскостью, в которую заключается данная прямая
(рис. 1.7.4).
S2
l2
2
S
22
22

32
A2
3
12
1
A2
A1
11
B2
31
2
C2
C1
12
32
B2
C
A
A1
21
B
B1
Рис. 1.7.3
l1 1
31
21
B1
11
Рис. 1.7.4
Контрольные вопросы:
1 Какие поверхности называют многогранниками?
2 Какие многогранники называются правильными?
3 Какими элементами задаются многогранники на чертеже?
4 Какая фигура сечения получается при пересечении многогранника плоскостью?
5 Алгоритм построения точек пересечения плоскости прямой?
Решить задачи: 48, 49, 50
Тема 8: «Аксонометрические проекции»
Общие сведения.
Аксонометрическая проекция (аксонометрия) представляет собой один
из видов наглядного изображения предметов, основанного на методе параллельного проецирования. Для построения аксонометрии предмет вместе с осями ординат проецируется на произвольно выбранную плоскость (П′ или П″)
называемую плоскостью аксонометрических проекций (рис. 1.8.1).
Слово “аксонометрия” – греческое. Оно состоит из двух слов «axcon» ось и «metro» - измеряю. Перевод этого слова означает измерение по осям, или
измерение параллельно осям, так как размеры изображаемого предмета на чер23
Рис. 1.8.1
теже откладываются только параллельно осям x, y, z, называемых аксонометрическими осями координат.
Аксонометрические проекции бывают:
- прямоугольные, если проецирующие лучи перпендикулярны аксонометрической плоскости проекций (изометрия, прямоугольная диметрия);
- косоугольные, если проецирующие лучи направлены под углом к аксонометрической плоскости проекций (фронтальная диметрия).
Прямоугольная изометрическая проекция.
«Изометрия» (греч) – равное измерение. При вычерчивании изометрической проекции коэффициенты искажения по осям x, y, z для простоты построения принимаются равными 1, т. е .размеры по всем трем осям откладываются
без искажения (натуральные) (к x = 1, к y = 1, к z = 1). Оси x, y, z в изометрической проекции располагаются между собой под углом 120º (рис.1.8.2).
Окружности в изометрии изображаются в виде эллипсов. Малая ось эллипса параллельна проекции нормали к соответствующей плоскости. Коэффициенты искажения по осям эллипса составляют: по большой оси к б.о . = 1,22 d, по
малой к м.о . = 0,71 d, где d – диаметр окружности (рис.1.8.3)
Фронтальная диметрическая проекция.
При вычерчивании фронтальной диметрической проекции коэффициенты
искажения по осям x и z принимаются равными 1 (к x = 1, к z = 1), так как плоскость xOy параллельна плоскости П′, а аксонометрические оси O′x′ и O′z′
взаимно перпендикулярны, для оси y коэффициент искажения принимается
24
равным 0,5 (к y = 0,5), так как по рекомендации государственного стандарz
z
°
90
30°
x
90°
90°
120°
y
x
Рис. 1.8.2
°
90
y
Рис. 1.8.3
та направление оси O′y′ выбирается по биссектрисе угла x′O′y′. Аксонометрические оси при построении фронтальной диметрии располагаются под определенными углами: ось x - горизонтально, ось z - вертикально, ось y – под углом 45º к горизонтальной оси (рис. 1.8.4).
Окружности во фронтальной диметрии изображаются в виде окружности
(в натуральную величину) в плоскости xOz, в виде эллипсов в двух других
плоскостях. Коэффициенты искажения по осям составляют: в плоскости xOz
(окружность) – к = 1 (Н. В.), в двух других (эллипс) - по большой оси
к б.о = 1,07 d, по малой к м.о . = 0,33 d, где d – диаметр окружности (рис. 1.8.5)
z
z
7°14'
°
90
x
45°
7°14'
x
y
y
Рис. 1.8.4
1.
2.
3.
4.
5.
Рис. 1.8.5
Контрольные вопросы:
Какие проекции называются аксонометрическими?
Какие виды аксонометрических проекций вы знаете?
Что называют коэффициентом искажения?
Назовите коэффициенты искажений по направлениям осей в прямоугольной
изометрии и фронтальной диметрии.
Укажите направления и величины осей эллипсов изометрических и фронтальных диметрических проекций окружностей при условии использования
приведенных коэффициентов искажения.
Решить задачи: 73, 74
25
Тема 9: «Поверхности»
Образование поверхностей
Кинематический способ
образования поверхностей – поАn
верхность рассматривается как
А2
А1
ln
непрерывное множество последовательных положений линии,
Направляющая
Образующая
l
2
перемещающейся в пространl1
стве по определённому закону
Рис. 1.9.1
(рис. 1.9.1).
Определитель поверхности – совокупность независимых условий, однозначно задающих поверхность в пространстве и на чертеже:    :
 - геометрическая часть,
i 2 S2
S2
Ф(l, m, S)
Ф(l, i, S )
состоит из геометрических элеменl2
l2
тов, оперируя которыми можно задать поверхность (рис. 1.9.2 а, б);
 - алгоритмическая часть,
m2
содержит перечень последовательных операций образования поверхi1 S1
S1
ности.
l1
m1
l1
Линейчатые поверхности –
образуются перемещением прямоа)
б)
линейной образующей по некотоРис. 1.9.2
рой направляющей (см. рис. 1.9.2 а)
Цилиндрическая поверхность – все образующие параллельны. Определитель: Ф (l, m) (рис. 1.9.3 а).
Коническая поверхность - образующие имеют общую точку пересечения.
Определитель: Ф (l, m, S) (рис. 1.9.3 б)
Поверхности вращения - образуются вращением образующей (прямолинейной (см. рис. 1.9.2 б) или криволинейной (рис. 1.9.4)) вокруг оси. Определитель: Ф (l, i).
m
l2
l
l
m2
m
m1
m
l1
а)
б)
Рис. 1.9.3
26
S2
l2
S
S1
l1
m2
m1