Взаимное положение прямой линии и плоскости, двух плоскостей

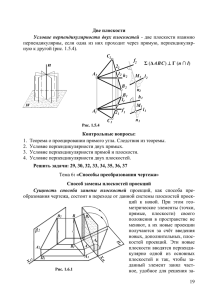
Лекция 5 СПОСОБЫ ПРЕОБРАЗОВАНИЯ ЧЕРТЕЖА
5.1 Способ перемены плоскостей проекций
5.2 Способ вращения
Многие задачи решаются легко и просто, если геометрические фигуры находятся в частном
положении. Рассмотрим два основных способа преобразования чертежа общего положения в частное положение:
1) Первый способ - заменяют заданную систему плоскостей проекций на новую так, чтобы
в ней исходные объекты оказались в частном положении, не меняя своего положения в пространстве (способ перемены плоскостей проекций);
2) Второй способ - изменяют положение исходных объектов в пространстве так, чтобы они
приняли частное положение относительно неизменных плоскостей проекций (способ вращения).
5.1 Способ перемены плоскостей проекций
Сущность способа перемены плоскостей проекций заключается в том, что положение точек, линий, плоских фигур, поверхностей в пространстве остается неизменным, а система  1 ,  2
дополняется плоскостями, образующими с плоскостью  1 или  2 , или между собой системы двух
взаимно перпендикулярных плоскостей, принимаемых за плоскости проекций.
Каждая новая перпендикулярная система выбирается так, чтобы по отношению к заданным
геометрическим элементам она заняла положение наиболее удобное для выполнения требуемого
задания. При введении новой плоскости проекций, ось проекций будет обозначаться в виде дроби,
черта которой лежит на оси, а обозначения плоскостей проекций представляют собой как бы числитель и знаменатель дроби, причем каждая буква ставится по ту сторону оси, где должны размещаться соответствующие проекции. Перемену плоскостей проекций можно производить последовательно несколько раз. Номер плоскости обозначает количество штрихов у проецируемых букв.
Пример построения проекции точки в новой системе координат приведён на рис.5.1 - для
горизонтально-проецирующей плоскости (при этом линия связи AA перпендикулярна оси
 1 /  2 и равны расстояния 1A  2 A ), и рис.5.2 - для фронтально-проецирующей плоскости
 3 (при этом линия связи AA перпендикулярна новой оси  2 /  3 и равны расстояния
1A  2 A ).
B’’
A’’’
A’’
A’’
2
1
A’’
2
2 3
2
1
B’
1
A’’’
A’
2
2
1
1
A’
A’
Рисунок 5.1
3 4
1
3
1 3
a
A’’’
Рисунок 5.2
B’’’
Рисунок 5.3
A’’’’
B’’’’
Выделим четыре основные задачи преобразования.
1)
Определение величины отрезка AB общего положения и угла наклона к плоскости
проекций приведено на рис.5.5. Натуральная величина AB равна AB  , a  ( AB^  1 )
и отмечены равные отложенные расстояния.
2)
Приведение отрезка прямой общего положения в проецирующее положение изображено на рис.5.5. Чтобы заданную в системе  1 ,  2 прямую общего положения AB , расположить перпендикулярно к дополнительной плоскости проекций, необходимо введение
двух дополнительных плоскостей проекций: сначала перейти к системе  3 ,  1 , в которой
 3   1 и AB  3 , а затем перейти к системе  3 ,  4 , где  3   4 и AB   4 - получим
точку - проекцию A(B ) данной прямой AB .
3)
Приведение плоской фигуры общего положения в проецирующее положение и угла
между данной плоскостью и плоскостью проекций. На рис.5.4 это осуществлено с помощью горизонтали, а на рис.5.5 – с помощью вертикали. Остальные построения показаны на
чертежах. На рис.5.5 определен   ( AB^  2 ) .
4)
Определение натурального вида плоской фигуры, расположенной в проецирующем
положении. Пример построения натурального вида ABC дан на рис.5.4. Здесь введены
две дополнительные плоскости проекций  3 и  4 по схеме:  3   1 и ABC   3 , а  3   4
и ABC  4 . То есть, в этом примере, чтобы получить параллельность плоскости ABC и
плоскости  4 , потребовалось предварительно расположить взаимно перпендикулярно
ABC и плоскости  3 .
5)
Определение расстояния между скрещивающимися прямыми AB и CD дано на
рис.5.6. Это расстояние выражается величиной общего перпендикуляра MN (зеленые линии) и заданными прямыми AB и CD . Для определения его длины удобно, чтобы одна из
прямых располагалась перпендикулярно плоскости проекций. Для этого надо последовательно ввести две плоскости проекций, например:  3 AB и  3   1 ; ось  1 /  3 AB и
D’’
B’’
N’’
B’’
D’’ Горизонталь
A’’
2
1
A’
C’’
2
1
C’’
1
4
A’’ M’’
3
B’
1 3
B’
V
2
B’’’ 3
4
A’’’
D’
C’
о
4
C’
C’’’
о
D’ A’
V
C’’’’
A’’’
B’’’’
2
1 3
A’’’’
B’’’
M’’’
3
C’’’’
Рисунок 5.4
N’
A’’’’B’’’’M’’’’
M’
N’’’’
1
C’’’
N’’’
D’’’’
D’’’
3 4
Рисунок 5.6
 4  AB и  3   4 ; ось  3 /  4  AB . На плоскости  4 прямая AB проецируется в точку
A(B ) . Проведя перпендикуляр из точки A(B ) на проекцию C D находим проекцию
N  точки N пересечения его с прямой CD . Отметим проекцию M  точки M, совпадающую с
проекциями точек A(B ) . Искомое расстояние определено. Это N M  . На чертеже стрелками указано построение проекций N M  и N M  общего перпендикуляра к двум скрещивающимся прямым в системе  1 /  2 .
2 3
B’’
A’’’
D’’
A’’
B’’’
f
C’’
C’’’
2
1
B’
A’
Фронталь
D’
C’
Рисунок 5.5
Например, для получения проекции точки пересечения двух профильных проекций AB и
CD лежащих в общей для них профильной плоскости необходима горизонтально-проецирующая
плоскость  3 в качестве вспомогательной плоскости проекций (как в примерах 5.3 или 5.4).
5.2 Способ вращения
При вращении некоторой точки вокруг оси она движется в плоскости вращения, перпендикулярной оси вращения, и описывает окружность некоторого радиуса. В качестве оси вращения
обычно используются прямые перпендикулярные или параллельные плоскости проекции.
При вращении точки вокруг вертикальной оси ее горизонтальная проекция перемещается
по окружности, а фронтальная проекция – параллельно оси х. Если точку вращения вокруг оси
перпендикулярной плоскости  2 , то ее фронтальная проекция будет перемещаться по окружности, а горизонтальная проекция - на плоскости  1 в виде отрезка прямой линии параллельно оси х.
Вращение вокруг проецирующей прямой применяют когда надо найти натуральную величину отрезка прямой и угол ее наклона. На рис.5.7 вращая точку В на угол  в положение B  , так,
что A B  параллельно плоскости  2 , определяется величина отрезка AB, равная AB  и угол a с
плоскостью  2 , здесь плоскости вращения перпендикулярны плоскости  1  и проходят через точку А поэтому точка B остается неподвижной.
A’’
A’’
A’’
C’’
A’’
B’’
a
B’’
D’’
C’’
C’’
B’’
B’’
B’’
X
X
C’
A’
B’
C’
C’

B’
B’
A’
A’
D’
D’
A’
Рисунок 5.7
B’
B’
Рисунок 5.8
На рис.5.8 применяется способ вращения без указанной осей для определения натуральной
величины треугольника ABC. Для этого выполнено два поворота плоскости общего положения,
так, что после первого поворота эта плоскость стала перпендикулярной плоскости  2 . Первый поворот вокруг оси, перпендикулярный плоскости  1 осуществлен с помощью горизонтали CD, так
что C D  перпендикулярна оси X . Горизонтальная проекция треугольника ABC сохраняет свой
вид и величину, но сменила положение A B C  . Точки A, B, C при таком повороте перемещаются
в плоскостях параллельныхплоскости  1 и проекции A, B , C  находятся на линиях связи
A A, B B, C  C  . Второй поворот, переводящий треугольник в положение параллельное  1 , проведен вокруг оси вращения перпендикулярной к  2 . Фронтальная проекция при таком повороте
сохраняет вид и величину, полученные после первого поворота, но заняла новое положение
A B  C  . Натуральная величина треугольника ABC отмечена зелеными линиями и равна A BC  .
B’’
A’’
D’’
C’’
O’’ 1’’
X
B’
A’*
A’
D’
O’
C’
A’
P
Q
B’
Рисунок 5.9
Здесь хотя оси и не указаны, но их можно легко найти. Если провести отрезки A A и
B B  , и через их середины провести перпендикуляры, то точки пересечения этих перпендикуляров
и будут являться проекцией оси вращения, перпендикулярной плоскости  2 
Применение способа вращения без указания осей несколько упрощает построения, но чертеж занимает несколько большую площадь.
Натуральную величину плоской фигуры можно определить вращением вокруг оси, параллельной плоскости проекции, одним поворотом приведя фигуру в положение, параллельное плоскости проекции.
На рис.5.9 в качестве оси проекции взята горизонталь CD. При этом точки треугольника
вращаются по окружности в плоскостях, перпендикулярных к оси. Точка С остается неподвижной.
Точка А перемещается в плоскости P, а точка В – в плоскости Q. Точка O является горизонтальным центром вращения точки А. OA горизонтальная проекция радиуса вращения точки А. Фронтальная проекция центра вращения – точка O  , а OA - фронтальная проекция радиуса вращения
точки А. Натуральная величина OA * радиуса вращения определена из прямоугольного треугольника OAA * , где AA*  A1 , получаем горизонтальную проекцию A (см. по стрелке). Проекция B  получается как пересечение D A с плоскостью Q, Фронтальная проекция повернутого
треугольника совпадает с фронтальной проекцией горизонтали C D и представляет собой прямую линию.
Таким образом, натуральной величиной треугольника ABC является треугольник A B C  .