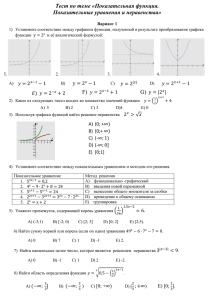
Формулы сокращенного умножения 2bab a ba + ± = ± 3 3 b ab ba

АЛГЕБРАИЧЕСКИЕ
УРАВНЕНИЯ
МНОЖИТЕЛИ. МЕТОД ИНТЕРВАЛОВ
ЗАНЯТИЕ 4.
И
НЕРАВЕНСТВА.
РАЗЛОЖЕНИЕ
НА
Необходимые сведения из теории.
Формулы сокращенного умножения
a  b 2  a 2  2ab  b2
a  b 3  a 3  3a 2b  3ab 2  b3
a 2  b 2  a  b a  b 
a 3  b3  a  b a 2  ab  b 2 
Формулы для нахождения корней квадратного уравнения
ax 2  bx  c  0
 b  b 2  4ac
2ab
Разложение на множители квадратного трехчлена
ax 2  bx  c  a( x  x1 )( x  x 2 )
Целым рациональным уравнением степени n стандартного вида называют уравнение
a0  a1 х  a2 х 2  ...  an x n =0, где аn  0 .
x1, 2 
Теорема 1: Если целое рациональное уравнение с целыми коэффициентами имеет целые корни, то
они являются делителями свободного члена этого уравнения.
Теорема 2: Если уравнение с целыми коэффициентами имеет рациональный корень х0 
p
p
, где
q
q
несократимая дробь, то p-делитель свободного члена а0 , a q это делитель аn- коэффициента при
старшей степени х.
Метод интервалов
Рациональным неравенством называется неравенство вида P(x) > 0 или P(x) < 0 ( P ( x)  0
или P ( x)  0 ), а так же
Р ( х)
0
Q( x)
 P ( x)

P( x)
P( x)

 0,
 0,
 0  где P(x) и Q(x) многочлены.
Q( x)
Q( x)
 Q( x)

Алгоритм метода интервалов
1. Разложить многочлены P(x) и Q(x) на линейные множители.
Количество множителей может быть любым, но обязательно в разностях каждого множителя x
всегда является уменьшаемым и коэффициенты при переменной x должны быть положительными
(канонический вид).
Если количество множителей, которые надо привести к каноническому виду, не четное, то знак
сравнения решаемого неравенства меняется на противоположный. Но если количество множителей,
которые надо привести к каноническому виду, четное, то знак сравнения решаемого неравенства
остается тем же.
2. Найти корень каждого множителя и нанести все корни на числовую ось.
Найти все корни - значит решить уравнения P(x) = 0 и Q(x) = 0. Отметить на числовой оси корни
уравнений в порядке возрастания. Эти числа разбивают числовую ось на интервалы. На каждом из
этих интервалов рациональное выражение сохраняет, а, переходя через отмеченные точки, меняет
знак на противоположный.
3. Определить знак неравенства справа от большего корня.
Расставить знаки на интервалах, начиная от крайнего правого. Так как все множители имеют
канонический вид, то над правым интервалом всегда ставится знак «+» и далее знаки чередуются.
4. Проставить знаки в остальных интервалах, учитывая чентое или нечетное число раз
встречается каждый корень.
Если корень выражения имеет четную степень (например: (x - 5)2 = 0, следовательно, x = 5 - корень
второй степни), то около этого корня выражение не меняет знака.
Если корень выражения имеет нечетную степень (например: (x - 5)3 = 0 , следовательно, x = 5 корень третей степни), то переходя через этот корень выражение меняет знак.
5.Выписать ответы неравенства в виде интервалов.
Для неравенства вида P(x) > ответом считается, объединение интервалов, на которых функция
сохраняет знак "+".
Для неравенства вида P(x) < 0 ответом считается, объединение интервалов, на которых функция
сохраняет знак "-".
Примеры решения задач
1. Решить уравнение х 4  2 х 3  11х 2  4 х  4  0 .
Решение:
Чтобы проверить наличие целых корней этого уравнения, выпишем все делители его свободного
члена:  1,  2,  4 . Подставляя по очереди эти числа в левую часть уравнения, находим, что числа
х1  1
и
х2  2
являются
корнями
уравнения,
т.е.
корнями
многочлена
Р4 ( х)  х  2 х  11х  4 х  4 . Многочлен P(x) делится на х-1 и на х-2. Значит, Р(х) делится и на
их произведение (х-1)(х-2)=х2-3х+2.
Выполним деление углом.
_x4 + 2x3 - 11x2 + 4x + 4 x2-3x+2
x4 - 3x3 + 2x2
_5x3 – 13x2 +4х
x2 + 5x +2
3
2
5x -15x + 10x
_ 2x2–6x + 4
2х2- 6х+4
0
Значит, многочлен Р(х) можно записать в виде
Р(х)=(х-1)(х-2)(х2+5х+2). Итак, первоначальное уравнение равносильно совокупности уравнений х1=0, х-2=0, х2+5х+2=0.
Решая каждое из этих уравнений, находим решение исходного уравнения: х1  1 , х2  2 ,
4
х3, 4 
3
2
 5  17
.
2
2. Рассмотрим два примера на применение метода
интервалов
3. Сократите дробь:
Решение:
5x 2  6x  1
.
4 x 2  5x  1
1
Находим нули числителя: х1=-1 и х2=  .
5
1
Находим нули знаменателя: х3=1 и х4=  .
4
Разложив на множители числитель и знаменатель, получим:
1
5( x  1)( x  )
5x  6x  1
5  5x  1 .

2
1
4x  1
4 x  5x  1
4( x  1)( x  )
4
2
6. Изобразить схематически график функции у 
х ( х  4) 2
х  32
.
Решение:
Найдем нули числителя и нули знаменателя:
Числитель обращается в ноль в точках х=0 и х=4. Знаменатель обращаетя в ноль при х=-3.
Так как на ноль делить нельзя, прямая х=-3 будет являться вертикальной асимптотой
графика функции.
Найдем промежутки знакопостоянства:
+
-
+
0
3
+
4
у
0
3
х
4
7. По известным промежуткам знакопостоянства восстановить функцию.
-
+
-3
+
-2
2
5
Решение:
В точках х=5 и х= - 2 функция существует и равна нулю. Это значит, при разложении функции на
множители будут присутствовать множители (х-5)2(х+2). Множитель (х-5) записан в квадрате,
потому что при переходе через корень х=5
Функция не поменяла свой знак. Но с тем же успехом, вместо второй мы могли использовать любую
чётную степень.
Функция не существует при х=-3 и х=2. И при переходе через эти точки функция меняет знак. Это
значит, что множители
(х+3) и (х-2) располагаются в знаменателе, причем каждый из них может быть в любой нечетной
степени, например (х+3)(х-2)3.
( x  5) 2 ( x  2)
, но так как при x   составленная нами
( x  3)( x  2) 3
функция f ( x)  0 , а судя по данным в условии промежуткам знакопостоянства при x   ,
Попытаемся составить функцию: f ( x) 
функция
f ( x)  
должна быть отрицательная, следовательно, мы должны изменить её знак :
( x  5) 2 ( x  2)
.
( x  3)( x  2) 3
Задачи для работы в аудитории
1. Решите уравнение, используя метод разложения на множители:
а) 9 х 3  18 х 2  х  2 ;
б) y 3  y 2  y  1 ;
в) x 3  3x 2  3x  1  0.
2. Решите уравнение.
а) х3  4 х 2  5 х  2  0
б) х 4  4 х 3  х 2  16 х  12  0
3. Сократить дробь
4 x 2  3x  1
5 x 2  26 x  5
; б)
;
а)
3x 2  4 x  1
3 x 2  16 x  5
6x 2  7x  2
3x 2  8 x  3
в)
;
г)
.
2 x 2  13x  7
6 x 2  17 x  3
x  2 6  ( x  10)( x  5)
f ( x) 
5
4. Пусть
2
.
x( x  9,8)
Решить неравенство: а) f ( x)  0 ; б) f ( x)  0 ; в) f ( x)  0 ; г) f ( x)  0 .
5. Решить неравенства методом интервалов:
3х  1
3х 2  10 х  3
х 2  9 (1  х)
 3 ; б) 2
 0 ; в)
 0.
а)
2х  5
(3  х) 2 (4  х 2 )
х  2 х  14
6. Изобразить схематически график функции.
х 1
х 2 ( х  2)
а) у 
.
; б) у  2
2
х ( х  5)
х  3
7. По известным промежуткам знакопостоянства восстановить функцию.

-
+
-3
а)
-
+
-
в)
-1
-3
б)

+
0
4
-1
-
+
0
+
-3
+
3
+
-
-1
1
Ответы к задачам для работы в аудитории


 1 
1.a)  ;2 ; б)  1 ; в)  1; 2  3 .
 3 
2.а)  2;1; б)  3;  1;  2.
5
4х  1
5х  1
3х  2
3х  1
; б)
; в)
; г)
.
3х  1
3х  1
x7
6х  1
4. f ( x)  0, x   ;  10   9,8; 0   2 6 ;   ;
3. а)




f ( x)  0, x   ;  10  (9,8; 0)  2 6 ; 5  5;  ;


f ( x)  0, x   10;9,8  0; 2 6  5 ;


f ( x)   10;9,8  0;2 6 .
 16 5 
5. а) х    ;   ; б) х   ;  3  1; 3 ;
2
 3
 2 
в) х   3;  2     ;2  .
 3 
6.а)
-3
2
6. б)
у
0
-5
1
х
7.
7. а) f ( x) 
в) f ( x) 
x 2 ( x  1)( x  3)
( x  1)( x  4) 2
; б) f ( x) 
;
x3
x( x  3)
x  42 ( x  5) 2 .
( x  3)(1  x)
Задачи для самостоятельных занятий
1. Решите уравнение, используя метод разложения на множители:
а) х3  х 2  4 х  4  0 ;
б) х3  3х 2  16 х  48  0 ;
б) х 4  3х 3  х  3  0 .
2. Решите уравнение.
a) 3х 4  5 х 3  9 х 2  9 х  10  0 ;
б) 4х4-16х3+21х2-11х+2=0.
3. Сократить дробь
5 x 2  11x  2
2x 2  x  1
5 x 2  26 x  5
; б)
; в)
.
а)
4x 2  9x  2
4x 2  8x  3
2x 2  9x  5
x  32 ( x  20)( x 
4. Пусть f ( x) 
10 ) 7
.
x( x  8,3) 2
Решить неравенство: а) f ( x)  0 ; б) f ( x)  0 ; в) f ( x)  0 ; г) f ( x)  0 .
5. Решить неравенства методом интервалов:
2х  1
х2  х  6
( х  1) 3
 2 ; б)
 0 ; в)
 0.
а)
3х  5
(9  х) 3
(5 х  10) 2 (1  3х)
6. Изобразить схематически график функции.
х( х  2) 2
х2
а) у 
; б) у  2
.
2
х ( х  4)
х  4
7. По известным промежуткам знакопостоянства восстановить функцию.

-
-3
а)
+
0
+
-3
-
+
4
-
+
-1
0
-
3
+
-3
в)
-
-1
-
б)

+
-1
-
1
5
Ответы к задачам для самостоятельных занятий
1.a)  2;1 ; б)  4  ; в) 3.
5 
1


2.а)  2;  ;1 ;б)  ;1; 2 .
3 

2

5х  1
2х  2
5х  1
; б)
; в)
.
3. а)
4х  1
4х  3
2х  1
4. f ( x)  0 , x   20;  8,3   8,3; 0  3  10 ;   ;



f ( x)  0, x   20;  8,3   8,3; 0  10 ;   ;


f ( x)  0, x   ;  20  0; 10 ;
f ( x)  0, x   ;  20  0; 3  (3; 10 ) .
 5 9
5. а) х    ;   ; б) х   ;  3  2; 9  ;
 3 8
1

в) х   ;  2    2;    1 .
3

6. а)
у
-
6. б)
0
2
х

у
-
4
0
х  4( х  1) ; б)
7. а) у 
х( х  3)
 ( х  5)( х  1)
.
в) у 
2
( х  1) 2  х  3
2
у
х
( х  3)( х  1)
;
х( х  3)
4 Задача для аттестационной работы 7 вариантов.
Решить неравенство
х  1( х  5) 3  0 .
1.
х2  4 х2

2.
3.
4.
5.
6.
7.

х  12 ( х  5) 3
х
2

х
2
 9 х2
х  4( х  3) 2
 25

х  3( х  1) 3
х
2
2
 0.

 0.

 0.
 4 х2
х  4( х  3) 2
х
 0.
1 х3
х  22 ( х  3)  0 .
х
2

 16 х 3
х  2
2
( х  3)
 0.
х  16 х

2

Ответы к 4 задаче аттестационной работы.
1.
2.
3.
4.
5.
6.
7.
х   ;  5   2; 0   0;1  2;    .
х   ;  5   3; 0   0; 3 .
х   5; 4  5;    .
х   2;1  2; 3 .
х   ;  1  0;1  4;   .
х   ;  4   0; 3  4;   .
х   4; 3   2  0; 4  .