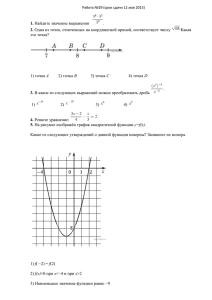
7. Геометрия

Мальчик прошел от дома по направлению на восток 450 м. Затем повернул на север и
прошел 240 м. На каком расстоянии (в метрах) от дома оказался мальчик?
Мальчик прошел от дома по направлению на восток 640 м. Затем повернул на север и
прошел 480 м. На каком расстоянии (в метрах) от дома оказался мальчик?
Мальчик прошел от дома по направлению на восток 560 м. Затем повернул на север и
прошел 330 м. На каком расстоянии (в метрах) от дома оказался мальчик?
Мальчик прошел от дома по направлению на восток 210 м. Затем повернул на север и
прошел 720 м. На каком расстоянии (в метрах) от дома оказался мальчик?
Мальчик прошел от дома по направлению на восток 840 м. Затем повернул на север и
прошел 800 м. На каком расстоянии (в метрах) от дома оказался мальчик?
Мальчик прошел от дома по направлению на восток 800 м. Затем повернул на север и
прошел 840 м. На каком расстоянии (в метрах) от дома оказался мальчик?
Девочка прошла от дома по направлению на запад 480 м. Затем повернула на север и
прошла 720 м. После этого она повернула на восток и прошла еще 480 м. На каком
расстоянии (в метрах) от дома оказалась девочка?
Девочка прошла от дома по направлению на запад 180 м. Затем повернула на север и
прошла 400 м. После этого она повернула на восток и прошла еще 480 м. На каком
расстоянии (в метрах) от дома оказалась девочка?
Девочка прошла от дома по направлению на запад 500 м. Затем повернула на север и
прошла 60 м. После этого она повернула на восток и прошла еще 500 м. На каком
расстоянии (в метрах) от дома оказалась девочка?
Девочка прошла от дома по направлению на запад 740 м. Затем повернула на север и
прошла 960 м. После этого она повернула на восток и прошла еще 460 м. На каком
расстоянии (в метрах) от дома оказалась девочка?
Девочка прошла от дома по направлению на запад 140 м. Затем повернула на север и
прошла 980 м. После этого она повернула на восток и прошла еще 140 м. На каком
расстоянии (в метрах) от дома оказалась девочка?
Девочка прошла от дома по направлению на запад 120 м. Затем повернула на север и
прошла 580 м. После этого она повернула на восток и прошла еще 120 м. На каком
расстоянии (в метрах) от дома оказалась девочка?
Девочка прошла от дома по направлению на запад 740 м. Затем повернула на север и
прошла 540 м. После этого она повернула на восток и прошла еще 740 м. На каком
расстоянии (в метрах) от дома оказалась девочка?
Девочка прошла от дома по направлению на запад 260 м. Затем повернула на север и
прошла 800 м. После этого она повернула на восток и прошла еще 260 м. На каком
расстоянии (в метрах) от дома оказалась девочка?
Девочка прошла от дома по направлению на запад 40 м. Затем повернула на север и
прошла 600 м. После этого она повернула на восток и прошла еще 40 м. На каком
расстоянии (в метрах) от дома оказалась девочка?
Девочка прошла от дома по направлению на запад 40 м. Затем повернула на север и
прошла 320 м. После этого она повернула на восток и прошла еще 280 м. На каком
расстоянии (в метрах) от дома оказалась девочка?
Мальчик и девочка, расставшись на перекрестке, пошли по взаимно перпендикулярным
дорогам, мальчик со скоростью 4 км/ч, девочка — 3 км/ч. Какое расстояние (в
километрах) будет между ними через 42 минуты?
Два парохода вышли из порта, следуя один на север, другой на запад. Скорости их равны
соответственно 18 км/ч и 24 км/ч. Какое расстояние (в километрах) будет между ними
через 5 часов?
Два парохода вышли из порта, следуя один на север, другой на запад. Скорости их равны
соответственно 24 км/ч и 10 км/ч. Какое расстояние (в километрах) будет между ними
через 3 часа?
Два парохода вышли из порта, следуя один на север, другой на запад. Скорости их равны
соответственно 12 км/ч и 16 км/ч. Какое расстояние (в километрах) будет между ними
через 4 часа?
В 24 м одна от другой растут две сосны. Высота одной 30 м, а другой — 12 м. Найдите
расстояние (в метрах) между их верхушками.
В 96 м одна от другой растут две сосны. Высота одной 38 м, а другой — 10 м. Найдите
расстояние (в метрах) между их верхушками.
В 40 м одна от другой растут две сосны. Высота одной 35 м, а другой — 26 м. Найдите
расстояние (в метрах) между их верхушками.
В 24 м одна от другой растут две сосны. Высота одной 17 м, а другой — 7 м. Найдите
расстояние (в метрах) между их верхушками.
В 15 м одна от другой растут две сосны. Высота одной 42 м, а другой — 6 м. Найдите
расстояние (в метрах) между их верхушками.
В 20 м одна от другой растут две сосны. Высота одной 45 м, а другой — 30 м. Найдите
расстояние (в метрах) между их верхушками.
В 36 м одна от другой растут две сосны. Высота одной 37 м, а другой — 10 м. Найдите
расстояние (в метрах) между их верхушками.
В 12 м одна от другой растут две сосны. Высота одной 29 м, а другой — 13 м. Найдите
расстояние (в метрах) между их верхушками.
В 105 м одна от другой растут две сосны. Высота одной 46 м, а другой — 10 м. Найдите
расстояние (в метрах) между их верхушками.
В 72 м одна от другой растут две сосны. Высота одной 30 м, а другой — 9 м. Найдите
расстояние (в метрах) между их верхушками.
В 120 м одна от другой растут две сосны. Высота одной 38 м, а другой — 16 м. Найдите
расстояние (в метрах) между их верхушками.
В 21 м одна от другой растут две сосны. Высота одной 48 м, а другой — 20 м. Найдите
расстояние (в метрах) между их верхушками.
В 48 м одна от другой растут две сосны. Высота одной 23 м, а другой — 3 м. Найдите
расстояние (в метрах) между их верхушками.
В 120 м одна от другой растут две сосны. Высота одной 41 м, а другой — 14 м. Найдите
расстояние (в метрах) между их верхушками.
Какой угол (в градусах) описывает часовая стрелка за 3 часа 52 минуты?
Какой угол (в градусах) описывает часовая стрелка за 5 часов 30 минут?
Какой угол (в градусах) описывает часовая стрелка за 4 часа 34 минуты?
Какой угол (в градусах) описывает часовая стрелка за 3 часа 18 минут?
Какой угол (в градусах) описывает часовая стрелка за 4 часа 24 минуты?
Какой угол (в градусах) описывает часовая стрелка за 1 час 30 минут?
Какой угол (в градусах) описывает часовая стрелка за 3 часа 12 минут?
Человек ростом 1,8 м стоит на расстоянии 9 шагов от столба, на котором висит фонарь.
Тень человека равна трем шагам. На какой высоте (в метрах) расположен фонарь?
Человек ростом 1,8 м стоит на расстоянии 15 шагов от столба, на котором висит фонарь.
Тень человека равна двум шагам. На какой высоте (в метрах) расположен фонарь?
Человек ростом 1,9 м стоит на расстоянии 15 шагов от столба, на котором висит фонарь.
Тень человека равна пяти шагам. На какой высоте (в метрах) расположен фонарь?
Человек ростом 1,5 м стоит на расстоянии 12 шагов от столба, на котором висит фонарь.
Тень человека равна двум шагам. На какой высоте (в метрах) расположен фонарь?
Человек ростом 1,7 м стоит на расстоянии 5 шагов от столба, на котором висит фонарь.
Тень человека равна пяти шагам. На какой высоте (в метрах) расположен фонарь?
Человек ростом 1,9 м стоит на расстоянии 12 шагов от столба, на котором висит фонарь.
Тень человека равна трем шагам. На какой высоте (в метрах) расположен фонарь?
Человек ростом 1,5 м стоит на расстоянии 20 шагов от столба, на котором висит фонарь.
Тень человека равна трем шагам. На какой высоте (в метрах) расположен фонарь?
Человек ростом 1,5 м стоит на расстоянии 8 шагов от столба, на котором висит фонарь.
Тень человека равна одному шагу. На какой высоте (в метрах) расположен фонарь?
Площадь прямоугольного земельного участка равна 16 га, ширина участка равна 250 м.
Найдите длину этого участка в метрах.
Площадь прямоугольного земельного участка равна 7 га, ширина участка равна 200 м.
Найдите длину этого участка в метрах.
Найдите периметр прямоугольного участка земли, площадь которого равна 14400 м2 и
одна сторона в 4 раза больше другой. Ответ дайте в метрах.
Найдите периметр прямоугольного участка земли, площадь которого равна 18000 м2 и
одна сторона в 5 раз больше другой. Ответ дайте в метрах.
Найдите периметр прямоугольного участка земли, площадь которого равна 67500 м2 и
одна сторона в 3 раза больше другой. Ответ дайте в метрах.
Два острых угла прямоугольного треугольника относятся как 1:89. Найдите больший острый угол. О
Два острых угла прямоугольного треугольника относятся как 2:43. Найдите больший
острый угол. Ответ дайте в градусах.
Два острых угла прямоугольного треугольника относятся как 2:3. Найдите больший
острый угол. Ответ дайте в градусах.
Два острых угла прямоугольного треугольника относятся как 1:14. Найдите больший
острый угол. Ответ дайте в градусах.
Два острых угла прямоугольного треугольника относятся как 41:49. Найдите больший
острый угол. Ответ дайте в градусах.
Разность углов, прилежащих к одной стороне параллелограмма, равна
. Найдите
меньший угол параллелограмма. Ответ дайте в градусах.
Разность углов, прилежащих к одной стороне параллелограмма, равна
меньший угол параллелограмма. Ответ дайте в градусах.
. Найдите
Разность углов, прилежащих к одной стороне параллелограмма, равна
меньший угол параллелограмма. Ответ дайте в градусах.
. Найдите
Разность углов, прилежащих к одной стороне параллелограмма, равна
меньший угол параллелограмма. Ответ дайте в градусах.
. Найдите
Разность углов, прилежащих к одной стороне параллелограмма, равна
меньший угол параллелограмма. Ответ дайте в градусах.
. Найдите
Один угол параллелограмма в девятнадцать раз больше другого. Найдите меньший угол.
Ответ дайте в градусах.
Один угол параллелограмма в 44 раза больше другого. Найдите меньший угол. Ответ
дайте в градусах.
Один угол параллелограмма в два раза больше другого. Найдите меньший угол. Ответ
дайте в градусах.
Один угол параллелограмма в 179 раз больше другого. Найдите меньший угол. Ответ
дайте в градусах.
Сумма двух углов равнобедренной трапеции равна
Ответ дайте в градусах.
Сумма двух углов равнобедренной трапеции равна
трапеции. Ответ дайте в градусах.
Сумма двух углов равнобедренной трапеции равна
Ответ дайте в градусах.
Сумма двух углов равнобедренной трапеции равна
трапеции. Ответ дайте в градусах.
. Найдите больший угол трапеции.
. Найдите больший угол
. Найдите больший угол трапеции.
. Найдите больший угол
Сумма двух углов равнобедренной трапеции равна
Ответ дайте в градусах.
. Найдите больший угол трапеции.
Сумма двух углов равнобедренной трапеции равна
Ответ дайте в градусах.
. Найдите больший угол трапеции.
Сумма двух углов равнобедренной трапеции равна
трапеции. Ответ дайте в градусах.
. Найдите меньший угол
Сумма двух углов равнобедренной трапеции равна
трапеции. Ответ дайте в градусах.
. Найдите меньший угол
Сумма двух углов равнобедренной трапеции равна
трапеции. Ответ дайте в градусах.
. Найдите меньший угол
Сумма двух углов равнобедренной трапеции равна
трапеции. Ответ дайте в градусах.
. Найдите меньший угол
Сумма двух углов равнобедренной трапеции равна
трапеции. Ответ дайте в градусах.
. Найдите меньший угол
Найдите меньший угол равнобедренной трапеции, если два ее угла относятся как 2:3.
Ответ дайте в градусах.
Найдите меньший угол равнобедренной трапеции, если два ее угла относятся как 1:179.
Ответ дайте в градусах.
Найдите меньший угол равнобедренной трапеции, если два ее угла относятся как 17:73.
Ответ дайте в градусах.
Найдите меньший угол равнобедренной трапеции, если два ее угла относятся как 7:53.
Ответ дайте в градусах.
Найдите меньший угол равнобедренной трапеции, если два ее угла относятся как 13:32.
Ответ дайте в градусах.
Сумма трех углов выпуклого четырехугольника равна
дайте в градусах.
. Найдите четвертый угол. Ответ
Сумма трех углов выпуклого четырехугольника равна
Ответ дайте в градусах.
. Найдите четвертый угол.
Сумма трех углов выпуклого четырехугольника равна
Ответ дайте в градусах.
. Найдите четвертый угол.
Сумма трех углов выпуклого четырехугольника равна
Ответ дайте в градусах.
. Найдите четвертый угол.
Сумма трех углов выпуклого четырехугольника равна
Ответ дайте в градусах.
. Найдите четвертый угол.
Сумма двух углов выпуклого четырехугольника равна
углов. Ответ дайте в градусах.
. Найдите сумму двух других
Сумма двух углов выпуклого четырехугольника равна
углов. Ответ дайте в градусах.
. Найдите сумму двух других
Сумма двух углов выпуклого четырехугольника равна
углов. Ответ дайте в градусах.
. Найдите сумму двух других
Сумма двух углов выпуклого четырехугольника равна
углов. Ответ дайте в градусах.
. Найдите сумму двух других
Сумма двух углов выпуклого четырехугольника равна
углов. Ответ дайте в градусах.
. Найдите сумму двух других
В выпуклом четырехугольнике ABCD
,
. Найдите угол A. Ответ дайте в градусах.
В выпуклом четырехугольнике ABCD
Найдите угол A. Ответ дайте в градусах.
В выпуклом четырехугольнике ABCD
Найдите угол A. Ответ дайте в градусах.
,
,
,
,
,
,
,
В выпуклом четырехугольнике ABCD
Найдите угол A. Ответ дайте в градусах.
,
,
В выпуклом четырехугольнике ABCD
Найдите угол A. Ответ дайте в градусах.
,
,
В выпуклом четырехугольнике ABCD
Найдите угол A. Ответ дайте в градусах.
,
,
.
,
,
.
.
,
.
,
.
Углы выпуклого четырехугольника относятся как 1:5:8:10. Найдите меньший угол. Ответ
дайте в градусах.
Углы выпуклого четырехугольника относятся как 2:12:14:17. Найдите меньший угол.
Ответ дайте в градусах.
Углы выпуклого четырехугольника относятся как 2:7:15:16. Найдите меньший угол. Ответ
дайте в градусах.
Углы выпуклого четырехугольника относятся как 2:7:8:13. Найдите меньший угол. Ответ
дайте в градусах.
Углы выпуклого четырехугольника относятся как 5:10:12:18. Найдите меньший угол.
Ответ дайте в градусах.
Два угла вписанного в окружность четырехугольника равны
и
. Найдите больший
из оставшихся углов. Ответ дайте в градусах.
Два угла вписанного в окружность четырехугольника равны
из оставшихся углов. Ответ дайте в градусах.
и
. Найдите больший
Два угла вписанного в окружность четырехугольника равны
больший из оставшихся углов. Ответ дайте в градусах.
и
. Найдите
Два угла вписанного в окружность четырехугольника равны
больший из оставшихся углов. Ответ дайте в градусах.
и
. Найдите
Два угла вписанного в окружность четырехугольника равны
больший из оставшихся углов. Ответ дайте в градусах.
и
. Найдите
Какие из следующих утверждений верны?
1) Через любые три точки проходит ровно одна прямая.
2) Сумма смежных углов равна
.
3) Если при пересечении двух прямых третьей прямой соответственные углы составляют в
сумме
, то эти две прямые параллельны.
4) Через любые две точки проходит не более одной прямой.
Какие из следующих утверждений верны?
1) Через любые три точки проходит не более одной прямой.
2) Через любые три точки проходит ровно одна прямая.
3) Если две параллельные прямые пересечены третьей прямой, то внутренние
односторонние углы равны.
4) Если при пересечении двух прямых третьей прямой соответственные углы составляют в
сумме
, то эти две прямые параллельны.
Какие из следующих утверждений верны?
1) Если две параллельные прямые пересечены третьей прямой, то внутренние
односторонние углы равны.
2) Через любую точку проходит более одной прямой.
3) Любые три прямые имеют не менее одной общей точки.
4) Любые две прямые имеют не менее одной общей точки.
Какие из следующих утверждений верны?
1) Если при пересечении двух прямых третьей прямой внутренние накрест лежащие углы
равны
, то две прямые параллельны.
2) Любые три прямые имеют не менее одной общей точки.
3) Если при пересечении двух прямых третьей прямой внутренние накрест лежащие углы
составляют в сумме
, то эти две прямые параллельны.
4) Сумма вертикальных углов равна
.
Какие из следующих утверждений верны?
1) Любые две прямые имеют не менее одной общей точки.
2) Если расстояние от точки до прямой меньше 1, то и длина любой наклонной,
проведенной из данной точки к прямой, меньше 1.
3) Если при пересечении двух прямых третьей прямой внутренние накрест лежащие углы
составляют в сумме
, то эти две прямые параллельны.
4) Через любую точку проходит более одной прямой.
Какие из следующих утверждений верны?
1) Если две параллельные прямые пересечены третьей прямой, то внутренние
односторонние углы равны.
2) Смежные углы равны.
3) Через любые две точки проходит не менее одной прямой.
4) Если угол равен
, то смежный с ним равен
.
Какие из следующих утверждений верны?
1) Если расстояние от точки до прямой меньше 1, то и длина любой наклонной,
проведенной из данной точки к прямой, меньше 1.
2) Через любую точку проходит ровно одна прямая.
3) Любые три прямые имеют не более одной общей точки.
4) Любые две прямые имеют не менее одной общей точки.
Какие из следующих утверждений верны?
1) Если при пересечении двух прямых третьей прямой внутренние накрест лежащие углы
составляют в сумме
, то эти две прямые параллельны.
2) Через любые две точки проходит не менее одной прямой.
3) Если две прямые перпендикулярны
перпендикулярны.
третьей
прямой, то эти
две прямые
4) Если расстояние от точки до прямой больше 1, то и длина любой наклонной,
проведенной из данной точки к прямой, больше 1.
Какие из следующих утверждений верны?
1) Если при пересечении двух прямых третьей прямой внутренние накрест лежащие углы
равны
, то две прямые параллельны.
2) Через любые три точки проходит ровно одна прямая.
3) Любые три прямые имеют не менее одной общей точки.
4) Через любые две точки проходит не менее одной прямой.
Какие из следующих утверждений верны?
1) Если расстояние от точки до прямой больше 1, то и длина любой наклонной,
проведенной из данной точки к прямой, больше 1.
2) Через любые три точки проходит ровно одна прямая.
3) Если две прямые перпендикулярны
перпендикулярны.
третьей
прямой, то эти
две прямые
4) Через любые три точки проходит не более одной прямой.
Какие из следующих утверждений верны?
1) Любые три прямые имеют не более одной общей точки.
2) Если при пересечении двух прямых третьей прямой внутренние накрест лежащие углы
составляют в сумме
, то эти две прямые параллельны.
3) Через любые три точки проходит не более одной прямой.
4) Через любые три точки проходит не менее одной прямой.
Какие из следующих утверждений верны?
1) Через любые две точки проходит не более одной прямой.
2) Любые две прямые имеют ровно одну общую точку.
3) Если расстояние от точки до прямой больше 1, то и длина любой наклонной,
проведенной из данной точки к прямой, больше 1.
4) Через любую точку проходит ровно одна прямая.
Какие из следующих утверждений верны?
1) Через любые три точки проходит не менее одной прямой.
2) Если расстояние от точки до прямой больше 1, то и длина любой наклонной,
проведенной из данной точки к прямой, больше 1.
3) Любые три прямые имеют не более одной общей точки.
4) Любые две прямые имеют ровно одну общую точку.
Какие из следующих утверждений верны?
1) Любые три прямые имеют не более одной общей точки.
2) Через любую точку проходит более одной прямой.
3) Если при пересечении двух прямых третьей прямой внутренние накрест лежащие углы
равны
, то две прямые параллельны.
4) Если две прямые перпендикулярны третьей прямой, то эти две прямые
перпендикулярны.
Какие из следующих утверждений верны?
1) Через любую точку проходит более одной прямой.
2) Через любые две точки проходит не более одной прямой.
3) Через любые две точки проходит не менее одной прямой.
4) Если при пересечении двух прямых третьей прямой внутренние накрест лежащие углы
составляют в сумме
, то эти две прямые параллельны.
Какие из следующих утверждений верны?
1) Через любую точку проходит более одной прямой.
2) Через любую точку проходит не менее одной прямой.
3) Через любые три точки проходит не более одной прямой.
4) Любые три прямые имеют не менее одной общей точки.
Какие из следующих утверждений верны?
1) Если при пересечении двух прямых третьей прямой внутренние односторонние углы
равны
и
, то эти две прямые параллельны.
2) Если угол равен
, то смежный с ним равен
.
3) Любые три прямые имеют не более одной общей точки.
4) Смежные углы равны.
Какие из следующих утверждений верны?
1) Сумма смежных углов равна
.
2) Через любые две точки проходит не более одной прямой.
3) Через любые две точки проходит не менее одной прямой.
4) Если расстояние от точки до прямой больше 1, то и длина любой наклонной,
проведенной из данной точки к прямой, больше 1.
Какие из следующих утверждений верны?
1) Через любые три точки проходит ровно одна прямая.
2) Если расстояние от точки до прямой больше 1, то и длина любой наклонной,
проведенной из данной точки к прямой, больше 1.
3) Если угол равен
, то смежный с ним равен
.
4) Через любую точку проходит более одной прямой.
Какие из следующих утверждений верны?
1) В треугольнике против меньшей стороны лежит меньший угол.
2) Каждая сторона треугольника меньше разности двух других сторон.
3) Если две стороны и угол одного треугольника соответственно равны двум сторонам и
углу другого треугольника, то такие треугольники равны.
4) Если три угла одного треугольника соответственно равны трем углам другого
треугольника, то такие треугольники равны.
Какие из следующих утверждений верны?
1) Если один угол треугольника больше
, то два других его угла меньше
.
2) Если две стороны треугольника равны 3 и 4, то его третья сторона меньше 7.
3) В треугольнике против меньшей стороны лежит больший угол.
4) Если все высоты треугольника меньше 1, то и все его стороны меньше 1.
Какие из следующих утверждений верны?
1) В треугольнике ABC, для которого
,
,
, угол A наибольший.
2) Если две стороны и угол одного треугольника соответственно равны двум сторонам и
углу другого треугольника, то такие треугольники равны.
3) Если основание и боковая сторона одного равнобедренного треугольника
соответственно равны основанию и боковой стороне другого равнобедренного
треугольника, то такие треугольники равны.
4) В треугольнике против большей стороны лежит меньший угол.
Какие из следующих утверждений верны?
1) Если две стороны и угол одного треугольника соответственно равны двум сторонам и
углу другого треугольника, то такие треугольники равны.
2) Каждая сторона треугольника не превосходит суммы двух других сторон.
3) В равнобедренном треугольнике имеется не более двух равных углов.
4) Если две стороны треугольника равны 3 и 5, то его третья сторона больше 2.
Какие из следующих утверждений верны?
1) Внешний угол треугольника равен сумме двух его внутрен-них углов.
2) Если один из углов равнобедренного треугольника равен
оставшихся углов равен
.
, то один из его
3) Каждая сторона треугольника больше суммы двух других сторон.
4) В равнобедренном треугольнике имеется не более двух равных углов.
Какие из следующих утверждений верны?
1) Каждая сторона треугольника не превосходит суммы двух других сторон.
2) В равнобедренном треугольнике имеется не более двух равных углов.
3) Каждая сторона треугольника меньше разности двух других сторон.
4) Если две стороны и угол одного треугольника соответственно равны двум сторонам и
углу другого треугольника, то такие треугольники равны.
Какие из следующих утверждений верны?
1) В треугольнике ABC, для которого
,
2) Если один угол треугольника больше
, то два других его угла меньше
,
, угол наименьший.
.
3) Если две стороны и угол одного треугольника соответственно равны двум сторонам и
углу другого треугольника, то такие треугольники равны.
4) Если основание и боковая сторона одного равнобедренного треугольника
соответственно равны основанию и боковой стороне другого равнобедренного
треугольника, то такие треугольники равны.
Какие из следующих утверждений верны?
1) В треугольнике против меньшей стороны лежит меньший угол.
2) Треугольник со сторонами 1, 2, 3 не существует.
3) Каждая сторона треугольника больше суммы двух других сторон.
4) В треугольнике ABC, для которого
,
, угол A наибольший.
,
Какие из следующих утверждений верны?
1) В треугольнике против меньшего угла лежит меньшая сторона.
2) В треугольнике против меньшей стороны лежит больший угол.
3) В треугольнике против меньшей стороны лежит меньший угол.
4) В треугольнике ABC, для которого
наибольшая.
,
, сторона AC
,
Какие из следующих утверждений верны?
1) Сумма углов треугольника не превосходит
.]
2) В треугольнике против большей стороны лежит меньший угол.
3) Каждая сторона треугольника больше суммы двух других сторон.
4) Если в треугольнике ABC углы A и B равны соответственно
угол этого треугольника с вершиной C равен
.
70^\circ$, то внешний
Какие из следующих утверждений верны?
1) Треугольник со сторонами 2, 3, 4 не существует.
2) Каждая сторона треугольника меньше разности двух других сторон.
3) В треугольнике ABC, для которого
,
, угол наименьший.
,
4) В треугольнике ABC, для которого
наименьшая.
,
, сторона BC
,
Какие из следующих утверждений верны?
1) Если один из углов равнобедренного треугольника равен
2) Если два угла треугольника равны
и
3) В треугольнике ABC, для которого
, то третий угол равен
,
4) Треугольник со сторонами 2, 3, 4 не существует.
Какие из следующих утверждений верны?
, то один из его оставшихся углов р
,
.
, сторона AB наибольшая.
1) Каждая сторона треугольника меньше разности двух других сторон.
2) Треугольник со сторонами 2, 3, 4 не существует.
3) Треугольник со сторонами 1, 2, 3 не существует.
4) В равнобедренном треугольнике имеется не менее двух равных углов.
Какие из следующих утверждений верны?
1) Если гипотенуза одного прямоугольного треугольника равна гипотенузе другого
прямоугольного треугольника, то такие треугольники равны.
2) Если все стороны треугольника меньше 1, то и все его высоты меньше 1.
3) В треугольнике
, для которого
,
, угол — наименьший.
,
4) В треугольнике против меньшего угла лежит меньшая сторона.
Какие из следующих утверждений верны?
1) Если в треугольнике
углы
угол этого треугольника с вершиной
и равны соответственно
равен
.
2) Если два угла треугольника меньше
3) Если два угла треугольника равны
и
, то внешний
, то его третий угол больше
и
.
, то третий угол равен
.
4) Треугольник со сторонами 2, 2, 3 существует.
Какие из следующих утверждений верны?
1) В треугольнике против меньшего угла лежит меньшая сторона.
2) В равнобедренном треугольнике имеется не менее двух равных углов.
3) Внешний угол треугольника больше каждого, не смежного с ним, внутреннего угла.
4) В равнобедренном треугольнике имеется не более двух равных углов.
Какие из следующих утверждений верны?
1) Если две стороны треугольника равны 3 и 4, то его третья сторона меньше 7.
2) В треугольнике
наибольший.
, для которого
,
,
, угол
—
3) В треугольнике против меньшего угла лежит меньшая сторона.
4) Если один из углов равнобедренного треугольника равен
оставшихся углов равен
.
, то один из его
Какие из следующих утверждений верны?
1) Если все стороны треугольника меньше 1, то и все его высоты меньше 1.
2) Если две стороны треугольника равны 3 и 4, то его третья сторона меньше 7.
3) Если два угла треугольника меньше
, то его третий угол больше
.
4) Треугольник со сторонами 1, 2, 3 не существует.
Какие из следующих утверждений верны?
1) В треугольнике
наибольший.
, для которого
,
,
, угол
—
2) Внешний угол треугольника больше каждого внутреннего угла.
3) Треугольник со сторонами 1, 2, 3 не существует.
4) В треугольнике против меньшего угла лежит меньшая сторона.
Какие из следующих утверждений верны?
1) Вписанные углы, опирающиеся на одну и ту же хорду окружности, равны.
2) Если расстояние от центра окружности до прямой равно диаметру окружности, то эти
прямая и окружность касаются.
3) Если радиус окружности равен 2, а расстояние от центра окружности до прямой равно
3, то эти прямая и окружность не имеют общих точек.
4) Если расстояние между центрами двух окружностей равно сумме их диаметров, то эти
окружности касаются.
Какие из следующих утверждений верны?
1) Если дуга окружности составляет
дугу, равен
.
, то центральный угол, опирающийся на эту
2) Если радиусы двух окружностей равны 3 и 5, а расстояние между их центрами равно 1,
то эти окружности пересекаются.
3) Если радиус окружности равен 3, а расстояние от центра окружности до прямой равно
2, то эти прямая и окружность пересекаются.
4) Вписанные углы окружности равны.
Какие из следующих утверждений верны?
1) Если радиус окружности и расстояние от центра окружности до прямой равны 2, то эти прямая и
2) Если две окружности касаются, то расстояние между их центрами равно сумме радиусов.
3) Если расстояние между центрами двух окружностей равно сумме их диаметров, то эти окружнос
4) Вписанные углы окружности равны.
Какие из следующих утверждений верны?
1) Вписанные углы, опирающиеся на одну и ту же хорду окружности, равны.
2) Если дуга окружности составляет
равен
.
, то центральный угол, опирающийся на эту дугу,
3) Если радиус окружности и расстояние от центра окружности до прямой равны 2, то эти
прямая и окружность касаются.
4) Если расстояние от центра окружности до прямой меньше диаметра окружности, то эти
прямая и окружность пересекаются.
Какие из следующих утверждений верны?
1) Вписанные углы окружности равны.
2) Через любые четыре точки, не принадлежащие одной прямой, проходит единственная
окружность.
3) Если расстояние между центрами двух окружностей меньше суммы радиусов, то эти
окружности пересекаются.
4) Если расстояние от центра окружности до прямой равно диаметру окружности, то эти
прямая и окружность касаются.
Какие из следующих утверждений верны?
1) Если расстояние между центрами двух окружностей равно сумме их диаметров, то эти
окружности касаются.
2) Через любые три точки проходит не более одной окружности.
3) Если радиусы двух окружностей равны 5 и 7, а расстояние между их центрами равно 3,
то эти окружности не имеют общих точек.
4) Вписанные углы окружности равны.
Какие из следующих утверждений верны?
1) Если дуга окружности составляет
окружности, равен
.
, то вписанный угол, опирающийся на эту дугу
2) Если радиусы двух окружностей равны 3 и 5, а расстояние между их центрами равно 1,
то эти окружности пересекаются.
3) Если расстояние между центрами двух окружностей равно сумме их диаметров, то эти
окружности касаются.
4) Если расстояние между центрами двух окружностей больше суммы их диаметров, то
эти окружности не имеют общих точек.
Какие из следующих утверждений верны?
1) Если вписанный угол равен
окружности, равен
.
, то центральный угол, опирающийся на ту же дугу
2) Через любые три точки проходит не более одной окружности.
3) Если радиусы двух окружностей равны 3 и 5, а расстояние между их центрами равно 1,
то эти окружности пересекаются.
4) Через любые четыре точки, не принадлежащие одной прямой, проходит единственная
окружность.
Какие из следующих утверждений верны?
1) Если вписанный угол равен
окружности, равен
.
, то центральный угол, опирающийся на ту же дугу
2) Вписанные углы окружности равны.
3) Если вписанный угол равен
равна
.
, то дуга окружности, на которую опирается этот угол,
4) Если дуга окружности составляет
равен
.
, то центральный угол, опирающийся на эту дугу,
Какие из следующих утверждений верны?
1) Если расстояние от центра окружности до прямой равно диаметру окружности, то эти
прямая и окружность касаются.
2) Если вписанный угол равен
равна
.
, то дуга окружности, на которую опирается этот угол,
3) Через любые три точки проходит не более одной окружности.
4) Если расстояние от центра окружности до прямой меньше диаметра окружности, то эти
прямая и окружность пересекаются.
Какие из следующих утверждений верны?
1) Если радиус окружности равен 3, а расстояние от центра окружности до прямой равно
2, то эти прямая и окружность пересекаются.
2) Через любые три точки проходит не более одной окружности.
3) Если расстояние от центра окружности до прямой равно диаметру окружности, то эти
прямая и окружность касаются.
4) Вписанные углы окружности равны.
Какие из следующих утверждений верны?
1) Если радиусы двух окружностей равны 3 и 5, а расстояние между их центрами равно 1,
то эти окружности пересекаются.
2) Если радиус окружности и расстояние от центра окружности до прямой равны 2, то эти
прямая и окружность касаются.
3) Вписанные углы окружности равны.
4) Если вписанный угол равен
окружности, равен
.
, то центральный угол, опирающийся на ту же дугу
Какие из следующих утверждений верны?
1) Через любые три точки проходит не более одной окружности.
2) Через любые четыре точки, не принадлежащие одной прямой, проходит единственная
окружность.
3) Если дуга окружности составляет
окружности, равен
.
, то вписанный угол, опирающийся на эту дугу
4) Если радиус окружности равен 3, а расстояние от центра окружности до прямой равно
2, то эти прямая и окружность пересекаются.
Какие из следующих утверждений верны?
1) Вписанные углы окружности равны.
2) Если радиус окружности равен 2, а расстояние от центра окружности до прямой равно
3, то эти прямая и окружность не имеют общих точек.
3) Через любые три точки проходит не более одной окружности.
4) Если расстояние между центрами двух окружностей меньше суммы радиусов, то эти
окружности пересекаются.
Какие из следующих утверждений верны?
1) Если расстояние между центрами двух окружностей больше суммы их диаметров, то
эти окружности не имеют общих точек.
2) Если расстояние от центра окружности до прямой равно диаметру окружности, то эти
прямая и окружность касаются.
3) Если расстояние от центра окружности до прямой больше диаметра окружности, то эти
прямая и окружность не имеют общих точек.
4) Если радиус окружности и расстояние от центра окружности до прямой равны 2, то эти
прямая и окружность касаются.
Какие из следующих утверждений верны?
1) Если радиусы двух окружностей равны 5 и 7, а расстояние между их центрами равно 3,
то эти окружности не имеют общих точек.
2) Если радиус окружности равен 2, а расстояние от центра окружности до прямой равно
3, то эти прямая и окружность не имеют общих точек.
3) Если дуга окружности составляет
окружности, равен
.
, то вписанный угол, опирающийся на эту дугу
4) Если радиусы двух окружностей равны 3 и 5, а расстояние между их центрами равно 8,
то эти окружности касаются.
Какие из следующих утверждений верны?
1) Через любые три точки проходит не более одной окружности.
2) Если расстояние от центра окружности до прямой меньше диаметра окружности, то эти
прямая и окружность пересекаются.
3) Если радиус окружности и расстояние от центра окружности до прямой равны 2, то эти
прямая и окружность касаются.
4) Если радиус окружности равен 2, а расстояние от центра окружности до прямой равно
3, то эти прямая и окружность не имеют общих точек.
Какие из следующих утверждений верны?
1) Через любые четыре точки, не принадлежащие одной прямой, проходит единственная
окружность.
2) Если радиус окружности равен 3, а расстояние от центра окружности до прямой равно
2, то эти прямая и окружность пересекаются.
3) Если вписанный угол равен
равна
.
, то дуга окружности, на которую опирается этот угол,
4) Если вписанный угол равен
окружности, равен
.
, то центральный угол, опирающийся на ту же дугу
Какие из следующих утверждений верны?
1) Если радиусы двух окружностей равны 3 и 5, а расстояние между их центрами равно 8,
то эти окружности касаются.
2) Если расстояние между центрами двух окружностей меньше суммы радиусов, то эти
окружности пересекаются.
3) Через любые две точки проходит не менее одной окружности.
4) Если дуга окружности составляет
дугу, равен
.
, то центральный угол, опирающийся на эту
Какие из следующих утверждений верны?
1) Если в четырехугольнике две стороны параллельны, то этот четырехугольник —
параллелограмм.
2) Диагонали параллелограмма равны.
3) Если один из углов, прилежащих к стороне параллелограмма, равен
угол, прилежащий к той же стороне, равен
.
, то другой
4) Сумма двух противоположных углов четырехугольника не превосходит
.
Какие из следующих утверждений верны?
1) Если один из углов параллелограмма равен
.
, то противоположный ему угол равен
2) Если основания трапеции равны 4 и 6, то средняя линия этой трапеции равна 10.
3) Диагонали квадрата равны.
4) Диагонали параллелограмма делят его углы пополам.
Какие из следующих утверждений верны?
1) Сумма двух противоположных углов четырехугольника не превосходит
.
2) Если в четырехугольнике две стороны параллельны, то этот четырехугольник —
параллелограмм.
3) Если противоположные углы выпуклого четырехугольника равны, то этот
четырехугольник — параллелограмм.
4) Сумма углов выпуклого четырехугольника равна
.
Какие из следующих утверждений верны?
1) Диагонали параллелограмма делят его углы пополам.
2) Если в четырехугольнике две стороны параллельны, то этот четырехугольник — параллелограмм
3) Диагонали параллелограмма равны.
4) Диагонали квадрата делят его углы пополам.
Какие из следующих утверждений верны?
1) Если в четырехугольнике две
четырехугольник — параллелограмм.
противоположные
стороны
равны,
то
этот
2) Диагонали квадрата делят его углы пополам.
3) Если один из углов параллелограмма равен
, то противоположный ему угол равен
.
4) Сумма двух противоположных углов параллелограмма равна
.
Какие из следующих утверждений верны?
1) Если один из углов, прилежащих к стороне параллелограмма, равен
угол, прилежащий к той же стороне, равен
.
2) Сумма углов выпуклого четырехугольника равна
, то другой
.
3) Диагонали параллелограмма перпендикулярны.
4) Сумма двух противоположных углов параллелограмма равна
.
Какие из следующих утверждений верны?
1) Сумма углов выпуклого четырехугольника равна
.
2) Если средняя линия трапеции равна 5, то сумма ее оснований равна 10.
3) Если сумма трех углов выпуклого четырехугольника равна
160^\circ$.
4) Диагонали параллелограмма равны.
Какие из следующих утверждений верны?
1) Диагонали квадрата делят его углы пополам.
2) Сумма углов выпуклого четырехугольника равна
.
3) Диагонали параллелограмма перпендикулярны.
4) Если в параллелограмме диагонали равны, то этот параллелограмм — прямоугольник.
Какие из следующих утверждений верны?
1) Если диагонали параллелограмма делят его углы пополам, то этот параллелограмм —
ромб.
2) Диагонали параллелограмма равны.
3) Сумма двух противоположных углов четырехугольника не превосходит
.
4) Если в параллелограмме диагонали перпендикулярны, то этот параллелограмм — ромб.
Какие из следующих утверждений верны?
1) Если в параллелограмме диагонали равны, то этот параллелограмм — прямоугольник.
2) Если в четырехугольнике две
четырехугольник — параллелограмм.
противоположные
стороны
равны,
то
этот
3) Если основания трапеции равны 4 и 6, то средняя линия этой трапеции равна 10.
4) Диагонали квадрата делят его углы пополам.
Какие из следующих утверждений верны?
1) Диагонали параллелограмма делят его углы пополам.
2) Если средняя линия трапеции равна 5, то сумма ее оснований равна 10.
3) Если в параллелограмме диагонали равны, то этот параллелограмм — прямоугольник.
4) Если в четырехугольнике две
четырехугольник — параллелограмм.
противоположные
стороны
равны,
то
этот
Какие из следующих утверждений верны?
1) Если в параллелограмме диагонали равны, то этот параллелограмм — прямоугольник.
2) Если один из углов, прилежащих к стороне параллелограмма, равен
угол, прилежащий к той же стороне, равен
.
3) Если противоположные углы выпуклого
четырехугольник — параллелограмм.
четырехугольника
, то другой
равны,
то
этот
4) Диагонали параллелограмма делят его углы пополам.
Какие из следующих утверждений верны?
1) Если сумма трех углов выпуклого четырехугольника равна
угол равен
.
, то его четвертый
2) Диагонали параллелограмма равны.
3) Диагонали квадрата делят его углы пополам.
4) Если в параллелограмме
параллелограмм — квадрат.
диагонали
равны
и
перпендикулярны,
то
этот
Какие из следующих утверждений верны?
1) Диагонали ромба в точке пересечения делятся пополам.
2) Если средняя линия трапеции равна 5, то сумма ее оснований равна 10.
3) Если один из углов параллелограмма равен
.
, то противоположный ему угол равен
4) Сумма углов параллелограмма, прилежащих к одной стороне, не превосходит
.
Какие из следующих утверждений верны?
1)
Если
противоположные
углы
выпуклого
четырехугольника
равны,
то
этот
четырехугольник — параллелограмм.
2) Если основания трапеции равны 4 и 6, то средняя линия этой трапеции равна 10.
3) Если в параллелограмме
параллелограмм — квадрат.
диагонали
равны
и
перпендикулярны,
то
этот
4) Если диагонали параллелограмма делят его углы пополам, то этот параллелограмм —
ромб.
Какие из следующих утверждений верны?
1) Если в параллелограмме диагонали перпендикулярны, то этот параллелограмм — ромб.
2) Если один из углов, прилежащих к стороне параллелограмма, равен
угол, прилежащий к той же стороне, равен
.
, то другой
3) Если один из углов, прилежащих к стороне параллелограмма, равен
угол, прилежащий к той же стороне, равен
.
, то другой
4) Сумма углов выпуклого четырехугольника больше
.
Какие из следующих утверждений верны?
1) Сумма углов параллелограмма, прилежащих к одной стороне, не превосходит
.
2) Диагонали квадрата делят его углы пополам.
3) Сумма двух противоположных углов параллелограмма равна
4) Если противоположные углы выпуклого
четырехугольник — параллелограмм.
.
четырехугольника
равны,
то
этот
Какие из следующих утверждений верны?
1) Около любой трапеции можно описать окружность.
2) Около любого ромба можно описать окружность.
3) Центром окружности, вписанной в треугольник, является точка пересечения
серединных перпендикуляров к его сторонам.
4) В любой четырехугольник можно вписать не более одной окружности.
Какие из следующих утверждений верны?
1) Центром окружности, вписанной в квадрат, является точка пересечения его
диагоналей.
2) В любой прямоугольник можно вписать окружность.
3) В любой правильный многоугольник можно вписать не менее одной окружности.
4) Около любой трапеции можно описать окружность.
Какие из следующих утверждений верны?
1) Центр окружности, описанной около остроугольного треугольника, находится внутри
этого треугольника.
2) В любой прямоугольник можно вписать окружность.
3) Центром окружности, вписанной в треугольник, является точка пересечения
серединных перпендикуляров к его сторонам.
4) Около любого ромба можно описать окружность.
Какие из следующих утверждений верны?
1) Центром окружности, вписанной в квадрат, является точка пересечения его
диагоналей.
2) Около любого ромба можно описать окружность.
3) Если стороны прямоугольника равны 3 и 4, то диаметр описанной около него
окружности, равен 5.
4) Центр окружности, вписанной в тупоугольный треугольник, находится вне этого
треугольника.
Какие из следующих утверждений верны?
1) Около любого ромба можно описать окружность.
2) Центр окружности, описанной около остроугольного треугольника, находится вне
этого треугольника.
3) Около любого правильного многоугольника можно описать не более одной
окружности.
4) Центром окружности, вписанной в квадрат, является точка пересечения его
диагоналей.
Какие из следующих утверждений верны?
1) Центр окружности, описанной около тупоугольного треугольника, находится внутри этого треуг
2) Центром окружности, вписанной в треугольник, является точка пересечения серединных перпенд
3) Центром окружности, вписанной в правильный треугольник, является точка пересечения медиан
4) Около любой трапеции можно описать окружность.
Какие из следующих утверждений верны?
1) Центр окружности, вписанной в тупоугольный треугольник, находится вне этого
треугольника.
2) Центр окружности, описанной около остроугольного треугольника, находится внутри
этого треугольника.
3) Центром окружности, вписанной в квадрат, является точка пересечения его диагоналей.
4) Около любого ромба можно описать окружность.
Какие из следующих утверждений верны?
1) Центром окружности, вписанной в треугольник, является точка пересечения
серединных перпендикуляров к его сторонам.
2) Около всякого четырехугольника можно описать не более одной окружности.
3) Центр окружности, описанной около тупоугольного треугольника, находится внутри
этого треугольника.
4) Центром окружности, описанной около квадрата, является точка пересечения его
диагоналей.
Какие из следующих утверждений верны?
1) Центром окружности, вписанной в правильный треугольник, является точка
пересечения медиан.
2) Около любой трапеции можно описать окружность.
3) Центр окружности, описанной около прямоугольного треугольника, находится на
стороне этого треугольника.
4) Около любого ромба можно описать окружность.
Какие из следующих утверждений верны?
1) В любой прямоугольник можно вписать окружность.
2) Центр окружности, описанной около прямоугольного треугольника, находится на
стороне этого треугольника.
3) Около всякого треугольника можно описать не более одной окружности.
4) Около любой трапеции можно описать окружность.
Какие из следующих утверждений верны?
1) Центр окружности, описанной около остроугольного треугольника, находится вне этого
треугольника.
2) Центром окружности, описанной около правильного треугольника является точка
пересечения высот.
3) В любой четырехугольник можно вписать не более одной окружности.
4) Центром окружности, вписанной в квадрат, является точка пересечения его диагоналей.
Какие из следующих утверждений верны?
1) Центр окружности, описанной около остроугольного треугольника, находится внутри
этого треугольника.
2) В любой прямоугольник можно вписать окружность.
3) Центр окружности, описанной около треугольника со сторонами, равными 3, 4, 5,
находится на стороне этого треугольника.
4) Центром окружности, вписанной в треугольник, является точка пересечения
серединных перпендикуляров к его сторонам.
Какие из следующих утверждений верны?
1) Около любого ромба можно описать окружность.
2) Центр окружности, описанной около остроугольного треугольника, находится внутри
этого треугольника.
3) В любой правильный многоугольник можно вписать не менее одной окружности.
4) Центром окружности, вписанной в треугольник, является точка пересечения
серединных перпендикуляров к его сторонам.
Какие из следующих утверждений верны?
1) Центром окружности, вписанной в правильный треугольник, является точка
пересечения медиан.
2) Центр окружности, описанной около остроугольного треугольника, находится вне этого
треугольника.
3) Центр окружности, описанной около остроугольного треугольника, находится внутри
этого треугольника.
4) Центр окружности, описанной около прямоугольного треугольника, находится на
стороне этого треугольника.
Какие из следующих утверждений верны?
1) Центром окружности, вписанной в правильный треугольник, является точка
пересечения медиан.
2) В любой правильный многоугольник можно вписать не менее одной окружности.
3) Центр окружности, вписанной в тупоугольный треугольник, находится вне этого
треугольника.
4) В любой треугольник можно вписать не менее одной окружности.
Какие из следующих утверждений верны?
1) Центром окружности, вписанной в правильный треугольник, является точка
пересечения медиан.
2) Центр окружности, описанной около прямоугольного треугольника, находится на
стороне этого треугольника.
3) Около всякого четырехугольника можно описать не более одной окружности.
4) Около любой трапеции можно описать окружность.
Какие из следующих утверждений верны?
1) Центром окружности, вписанной в правильный треугольник, является точка
пересечения медиан.
2) Центр окружности, описанной около остроугольного треугольника, находится вне
этого треугольника.
3) Около всякого треугольника можно описать не более одной окружности.
4) Около всякого четырехугольника можно описать не более одной окружности.
Какие из следующих утверждений верны?
1) Центром окружности, описанной около правильного треугольника является точка
пересечения высот.
2) В любой четырехугольник можно вписать не более одной окружности.
3) Если стороны прямоугольника равны 3 и 4, то диаметр описанной около него
окружности, равен 5.
4) Центр окружности, описанной около тупоугольного треугольника, находится внутри
этого треугольника.
Какие из следующих утверждений верны?
1) Центр окружности, описанной около прямоугольного треугольника, находится на
стороне этого треугольника.
2) В любой правильный многоугольник можно вписать не менее одной окружности.
3) Центром окружности, вписанной в квадрат, является точка пересечения его
диагоналей.
4) Центр окружности, описанной около треугольника со сторонами, равными 3, 4, 5,
находится на стороне этого треугольника.
Какие из следующих утверждений верны?
1) Правильный шестиугольник имеет центр симметрии.
2) Две центрально-симметричные прямые перпендикулярны.
3) Окружность имеет бесконечно много центров симметрии.
4) Прямоугольник не имеет центра симметрии.
Какие из следующих утверждений верны?
1) Центром симметрии квадрата является точка пересечения его диагоналей.
2) Прямая не имеет осей симметрии.
3) Квадрат имеет две оси симметрии.
4) Правильный шестиугольник имеет три оси симметрии.
Какие из следующих утверждений верны?
1) Правильный шестиугольник имеет шесть осей симметрии.
2) Правильный шестиугольник не имеет центра симметрии.
3) Правильный пятиугольник имеет центр симметрии.
4) Окружность имеет бесконечно много центров симметрии.
Какие из следующих утверждений верны?
1) Круг не имеет центра симметрии.
2) Прямая не имеет центра симметрии.
3) Равнобедренный треугольник имеет три оси симметрии.
4) Центром симметрии квадрата является точка пересечения его диагоналей.
Какие из следующих утверждений верны?
1) Круг не имеет центра симметрии.
2) Центром симметрии ромба является точка пересечения его диагоналей.
3) Прямая не имеет центра симметрии.
4) Окружность не имеет центра симметрии.
Какие из следующих утверждений верны?
1) Ромб не имеет центра симметрии.
2) Квадрат не имеет центра симметрии.
3) Центром симметрии ромба является точка пересечения его диагоналей.
4) Круг имеет одну ось симметрии.
Какие из следующих утверждений верны?
1) Круг не имеет центра симметрии.
2) Круг имеет бесконечно много центров симметрии.
3) Правильный пятиугольник не имеет центра симметрии.
4) Правильный шестиугольник имеет шесть осей симметрии.
Какие из следующих утверждений верны?
1) Прямая не имеет центра симметрии.
2) Правильный шестиугольник имеет шесть осей симметрии.
3) Равнобедренная трапеция не имеет центра симметрии.
4) Квадрат имеет две оси симметрии.
Какие из следующих утверждений верны?
1) Круг не имеет центра симметрии.
2) Равнобедренный треугольник не имеет центра симметрии.
3) Равнобедренная трапеция не имеет центра симметрии.
4) Параллелограмм имеет две оси симметрии.
Какие из следующих утверждений верны?
1) Прямоугольник не имеет центра симметрии.
2) Правильный шестиугольник имеет три оси симметрии.
3) Правильный шестиугольник имеет шесть осей симметрии.
4) Центром симметрии прямоугольника является точка пересечения диагоналей.
Какие из следующих утверждений верны?
1) Правильный шестиугольник имеет шесть осей симметрии.
2) Окружность имеет бесконечно много центров симметрии.
3) Две центрально-симметричные прямые перпендикулярны.
4) Центром симметрии прямоугольника является точка пересечения диагоналей.
Какие из следующих утверждений верны?
1) Квадрат имеет две оси симметрии.
2) Правильный пятиугольник не имеет центра симметрии.
3) Равнобедренный треугольник не имеет центра симметрии.
4) Прямоугольник не имеет центра симметрии.
Какие из следующих утверждений верны?
1) Две центрально-симметричные прямые перпендикулярны.
2) Правильный пятиугольник не имеет центра симметрии.
3) Правильный шестиугольник имеет шесть осей симметрии.
4) Равнобедренный треугольник имеет единственную ось симметрии.
Какие из следующих утверждений верны?
1) Круг имеет бесконечно много центров симметрии.
2) Равнобедренная трапеция не имеет центра симметрии.
3) Центром симметрии прямоугольника является точка пересечения диагоналей.
4) Правильный шестиугольник имеет шесть осей симметрии.
Какие из следующих утверждений верны?
1) Квадрат не имеет центра симметрии.
2) Равнобедренная трапеция не имеет центра симметрии.
3) Центром симметрии ромба является точка пересечения его диагоналей.
4) Правильный шестиугольник имеет центр симметрии.
Какие из следующих утверждений верны?
1) Центром симметрии квадрата является точка пересечения его диагоналей.
2) Прямая не имеет центра симметрии.
3) Правильный пятиугольник не имеет центра симметрии.
4) Равнобедренный треугольник не имеет центра симметрии.
Какие из следующих утверждений верны?
1) Круг имеет бесконечно много центров симметрии.
2) Центром симметрии квадрата является точка пересечения его диагоналей.
3) Правильный шестиугольник имеет шесть осей симметрии.
4) Центром симметрии ромба является точка пересечения его диагоналей.
Какие из следующих утверждений верны?
1) Центром симметрии квадрата является точка пересечения его диагоналей.
2) Центром симметрии равнобедренного прямоугольного треугольника является середина
гипотенузы.
3) Правильный пятиугольник имеет пять осей симметрии.
4) Центром симметрии ромба является точка пересечения его диагоналей.
Какие из следующих утверждений верны?
1) Правильный пятиугольник имеет пять осей симметрии.
2) Правильный шестиугольник имеет шесть осей симметрии.
3) Центром симметрии равнобедренного прямоугольного треугольника является середина
гипотенузы.
4) Равнобедренный треугольник не имеет центра симметрии.
Какие из следующих утверждений верны?
1) Если угол одного треугольника равен углу другого треугольника, то такие
треугольники подобны.
2) Стороны треугольника пропорциональны косинусам противолежащих углов.
3) Треугольник ABC, у которого
,
,
, является остроугольным.
4) Если два угла одного треугольника соответственно пропорциональны двум углам
другого треугольника, то такие треугольники подобны.
Какие из следующих утверждений верны?
1) Если две стороны и угол между ними одного треугольника соответственно равны двум
сторонам и углу между ними другого треугольника, то такие треугольники подобны.
2) Треугольник ABC, у которого
,
,
, является прямоугольным.
3) Если два угла одного треугольника соответственно пропорциональны двум углам
другого треугольника, то такие треугольники подобны.
4) Любые два прямоугольных треугольника подобны.
Какие из следующих утверждений верны?
1) В прямоугольном треугольнике квадрат гипотенузы не превосходит суммы квадратов
катетов.
2) Любые два равнобедренных треугольника подобны.
3) Квадрат любой стороны треугольника равен сумме квадратов двух других сторон без
удвоенного произведения этих сторон на синус угла между ними.
4) Треугольник ABC, у которого
,
,
, является прямоугольным.
Какие из следующих утверждений верны?
1) В прямоугольном треугольнике квадрат гипотенузы не превосходит суммы квадратов
катетов.
2) Стороны треугольника пропорциональны косинусам противолежащих углов.
3) Стороны треугольника пропорциональны синусам прилежащих углов.
4) Треугольник ABC, у которого
,
,
, является прямоугольным.
Какие из следующих утверждений верны?
1) Любые два равнобедренных треугольника подобны.
2) Треугольник ABC, у которого
,
,
, является прямоугольным.
3) В прямоугольном треугольнике квадрат гипотенузы не превосходит суммы квадратов
катетов.
4) Любые два прямоугольных треугольника подобны.
Какие из следующих утверждений верны?
1) Если два угла одного треугольника соответственно пропорциональны двум углам
другого треугольника, то такие треугольники подобны.
2) Если катеты прямоугольного треугольника равны 5 и 12, то его гипотенуза равна 13.
3) Любые два равнобедренных треугольника подобны.
4) Если два треугольника подобны, то их соответствующие стороны равны.
Какие из следующих утверждений верны?
1) Любые два равнобедренных треугольника подобны.
2) Если катет и гипотенуза прямоугольного треугольника равны соответственно 6 и 10, то
второй катет этого треугольника равен 8.
3) В прямоугольном треугольнике квадрат катета равен разности квадратов гипотенузы и
другого катета.
4) Если угол одного треугольника равен углу другого треугольника, то такие
треугольники подобны.
Какие из следующих утверждений верны?
1) Если катеты прямоугольного треугольника равны 5 и 12, то его гипотенуза равна 13.
2) Если два угла одного треугольника соответственно пропорциональны двум углам
другого треугольника, то такие треугольники подобны.
3) Любые два равносторонних треугольника подобны.
4) Любые два равнобедренных треугольника подобны.
Какие из следующих утверждений верны?
1) Квадрат любой стороны треугольника равен сумме квадратов двух других сторон без
удвоенного произведения этих сторон на синус угла между ними.
2) Любые два равносторонних треугольника подобны.
3) Треугольник ABC, у которого
,
,
, является прямоугольным.
4) В прямоугольном треугольнике квадрат гипотенузы не превосходит суммы квадратов
катетов.
Какие из следующих утверждений верны?
1) Любые два равнобедренных треугольника подобны.
2) Любые два равносторонних треугольника подобны.
3) Если два угла одного треугольника соответственно пропорциональны двум углам
другого треугольника, то такие треугольники подобны.
4) Если две стороны и угол между ними одного треугольника соответственно равны двум
сторонам и углу между ними другого треугольника, то такие треугольники подобны.
Какие из следующих утверждений верны?
1) Стороны треугольника пропорциональны синусам прилежащих углов.
2) Если угол одного треугольника равен углу другого треугольника, то такие
треугольники подобны.
3) Квадрат любой стороны треугольника равен сумме квадратов двух других сторон без
произведения этих сторон на косинус угла между ними.
4) Любые два прямоугольных и равнобедренных треугольника подобны.
Какие из следующих утверждений верны?
1) Если два угла одного треугольника соответственно пропорциональны двум углам
другого треугольника, то такие треугольники подобны.
2) Стороны треугольника пропорциональны косинусам противолежащих углов.
3) Треугольник ABC, у которого
,
,
, является остроугольным.
4) Если катет и гипотенуза прямоугольного треугольника равны соответственно 6 и 10, то
второй катет этого треугольника равен 8.
Какие из следующих утверждений верны?
1) Если две стороны и угол между ними одного треугольника соответственно равны двум
сторонам и углу между ними другого треугольника, то такие треугольники подобны.
2) Если катеты прямоугольного треугольника равны 5 и 12, то его гипотенуза равна 13.
3) В прямоугольном треугольнике квадрат гипотенузы не превосходит суммы квадратов
катетов.
4) Треугольник ABC, у которого
,
,
, является тупоугольным.
Какие из следующих утверждений верны?
1) Квадрат любой стороны треугольника равен сумме квадратов двух других сторон без
произведения этих сторон на косинус угла между ними.
2) Треугольник ABC, у которого
,
,
, является остроугольным.
3) Если две стороны и угол между ними одного треугольника соответственно равны двум
сторонам и углу между ними другого треугольника, то такие треугольники подобны.
4) Любые два прямоугольных треугольника подобны.
Какие из следующих утверждений верны?
1) Треугольник ABC, у которого
,
,
, является тупоугольным.
2) Квадрат любой стороны треугольника равен сумме квадратов двух других сторон без
произведения этих сторон на косинус угла между ними.
3) Если две стороны и угол между ними одного треугольника соответственно равны двум
сторонам и углу между ними другого треугольника, то такие треугольники подобны.
4) Если катеты прямоугольного треугольника равны 5 и 12, то его гипотенуза равна 13.
Какие из следующих утверждений верны?
1) Любые два прямоугольных и равнобедренных треугольника подобны.
2) В прямоугольном треугольнике квадрат катета равен разности квадратов гипотенузы и
другого катета.
3) Квадрат любой стороны треугольника равен сумме квадратов двух других сторон без
удвоенного произведения этих сторон на синус угла между ними.
4) Треугольник ABC, у которого
,
,
, является остроугольным.
Какие из следующих утверждений верны?
1) Если катет и гипотенуза прямоугольного треугольника равны соответственно 6 и 10, то
второй катет этого треугольника равен 8.
2) Если два треугольника подобны, то их соответствующие стороны равны.
3) Любые два прямоугольных и равнобедренных треугольника подобны.
4) Любые два равносторонних треугольника подобны.
Какие из следующих утверждений верны?
1) Треугольник ABC, у которого
,
,
, является остроугольным.
2) Если катеты прямоугольного треугольника равны 5 и 12, то его гипотенуза равна 13.
3) Если два угла одного треугольника соответственно пропорциональны двум углам
другого треугольника, то такие треугольники подобны.
4) Если катет и гипотенуза прямоугольного треугольника равны соответственно 6 и 10, то
второй катет этого треугольника равен 8.
Какие из следующих утверждений верны?
1) Квадрат любой стороны треугольника равен сумме квадратов двух других сторон без
произведения этих сторон на косинус угла между ними.
2) В прямоугольном треугольнике квадрат гипотенузы не превосходит суммы квадратов
катетов.
3) Любые два равносторонних треугольника подобны.
4) Стороны треугольника пропорциональны синусам прилежащих углов.
Какие из следующих утверждений верны?
1) Площадь круга равна произведению длины его окружности на радиус.
2) Если диагонали ромба равна 3 и 4, то его площадь равна 6.
3) Площадь прямоугольного треугольника равна произведению его катетов.
4) Если радиус круга равен 4, то его площадь равна 8.
Какие из следующих утверждений верны?
1) Площадь треугольника равна произведению его стороны на высоту, проведенную к
этой стороне.
2) Если площади фигур равны, то равны и сами фигуры.
3) Площадь круга равна четверти произведения длины его окружности на диаметр.
4) Если катеты прямоугольного треугольника равны 3 и 4, то его площадь равна 12.
Какие из следующих утверждений верны?
1) Отношение площадей подобных фигур равно коэффициенту подобия.
2) Если площади фигур равны, то равны и сами фигуры.
3) Если катеты прямоугольного треугольника равны 3 и 4, то его площадь равна 12.
4) Площадь прямоугольного треугольника меньше произведения его катетов.
Какие из следующих утверждений верны?
1) Если радиус круга равен 4, то его площадь равна 8.
2) Площадь параллелограмма равна произведению двух его сторон на косинус угла между
ними.
3) Площадь трапеции меньше произведения суммы оснований на высоту.
4) Площадь трапеции равна произведению суммы оснований на высоту.
Какие из следующих утверждений верны?
1) Если две стороны треугольника равны 4 и 5, а угол между ними равен
этого треугольника равна 10.
, то площадь
2) Площадь многоугольника, описанного около окружности, равна произведению его
периметра на радиус вписанной окружности.
3) Площадь трапеции не превосходит произведения средней линии на высоту.
4) Отношение площадей подобных фигур равно коэффициенту подобия.
Какие из следующих утверждений верны?
1) Если катеты прямоугольного треугольника равны 3 и 4, то его площадь равна 12.
2) Если радиус круга равен 4, то его площадь равна 8.
3) Площадь прямоугольного треугольника равна произведению его катетов.
4) Площадь ромба равна произведению двух его смежных сторон на синус угла между
ними.
Какие из следующих утверждений верны?
1) Площадь параллелограмма равна произведению двух его сторон на косинус угла между
ними.
2) Площадь многоугольника, описанного около окружности, равна четверти произведения
его периметра на диаметр вписанной окружности.
3) Если радиус круга равен 4, то его площадь равна 8.
4) Если диагонали ромба равна 3 и 4, то его площадь равна 6.
Какие из следующих утверждений верны?
1) Если радиус круга равен 4, то его площадь равна 8.
2) Площадь круга равна четверти произведения длины его окружности на диаметр.
3) Площадь треугольника равна произведению его стороны на высоту, проведенную к
этой стороне.
4) Площадь трапеции меньше произведения суммы оснований на высоту.
Какие из следующих утверждений верны?
1) Площадь круга равна четверти произведения длины его окружности на диаметр.
2) Площадь треугольника равна произведению его стороны на высоту, проведенную к
этой стороне.
3) Если площадь круга равна 4, то его радиус равен 2.
4) Площадь прямоугольника равна произведению двух его сторон.
Какие из следующих утверждений верны?
1) Отношение площадей подобных фигур равно коэффициенту подобия.
2) Если стороны правильного шестиугольника увеличить в три раза, то его площадь
увеличится в 9 раз.
3) Площадь ромба равна произведению двух его смежных сторон на синус угла между
ними.
4) Если две стороны треугольника равны 4 и 5, а угол между ними равен
этого треугольника равна 10.
, то площадь
Какие из следующих утверждений верны?
1) Площадь круга равна четверти произведения длины его окружности на диаметр.
2) Площадь треугольника не превосходит половины произведения двух его сторон на
синус угла между ними.
3) Если площади фигур равны, то равны и сами фигуры.
4) Если площадь круга равна 4, то его радиус равен 2.
Какие из следующих утверждений верны?
1) Если сторона треугольника равна 5, а высота, проведенная к этой стороне, равна 4, то
площадь этого треугольника равна 20.
2) Площадь многоугольника, описанного около окружности, равна произведению его
периметра на радиус вписанной окружности.
3) Площадь многоугольника, описанного около окружности, равна четверти произведения
его периметра на диаметр вписанной окружности.
4) Если стороны правильного шестиугольника увеличить в три раза, то его площадь
увеличится в 9 раз.
Какие из следующих утверждений верны?
1) Площадь треугольника не превосходит половины произведения двух его сторон на
синус угла между ними.
2) Площадь круга равна четверти произведения длины его окружности на диаметр.
3) Если катеты прямоугольного треугольника равны 3 и 4, то его площадь равна 12.
4) Если периметр многоугольника, описанного около окружности радиуса 2, равен 20, то
его площадь равна 20.
Какие из следующих утверждений верны?
1) Если стороны правильного шестиугольника увеличить в три раза, то его площадь
увеличится в 9 раз.
2) Площадь прямоугольника равна произведению двух его сторон.
3) Площадь многоугольника, описанного около окружности, равна четверти произведения
его периметра на диаметр вписанной окружности.
4) Площадь прямоугольного треугольника равна произведению его катетов.
Какие из следующих утверждений верны?
1) Если диагонали ромба равна 3 и 4, то его площадь равна 6.
2) Площадь ромба равна произведению двух его смежных сторон на синус угла между
ними.
3) Площадь ромба равна произведению его стороны на высоту, проведенную к этой
стороне.
4) Если сторона треугольника равна 5, а высота, проведенная к этой стороне, равна 4, то
площадь этого треугольника равна 20.
Какие из следующих утверждений верны?
1) Если катеты прямоугольного треугольника равны 3 и 4, то его площадь равна 12.
2) Площадь трапеции не превосходит произведения средней линии на высоту.
3) Если средняя линия трапеции равна 5, а высота равна 3, то площадь этой трапеции
равна 15.
4) Если диагонали ромба равна 3 и 4, то его площадь равна 6.
Какие из следующих утверждений верны?
1) Площадь многоугольника, описанного около окружности, равна четверти произведения
его периметра на диаметр вписанной окружности.
2) Площадь треугольника равна половине произведения его стороны на высоту,
проведенную к этой стороне.
3) Если диагонали ромба равна 3 и 4, то его площадь равна 6.
4) Площадь треугольника равна произведению его стороны на высоту, проведенную к
этой стороне.
Какие из следующих утверждений верны?
1) Площадь ромба равна произведению двух его смежных сторон на синус угла между
ними.
2) Площадь ромба равна произведению его стороны на высоту, проведенную к этой
стороне.
3) Площадь трапеции не превосходит произведения средней линии на высоту.
4) Если площадь круга равна 4, то его радиус равен 2.
Какие из следующих утверждений верны?
1) Две центрально-симметричные прямые перпендикулярны.
2) Если один угол треугольника больше
, то два других его угла меньше
.
3) В прямоугольном треугольнике квадрат катета равен разности квадратов гипотенузы и
другого катета.
4) Если две окружности касаются, то расстояние между их центрами равно сумме
радиусов.
Какие из следующих утверждений верны?
1) Если два угла треугольника меньше
, то его третий угол больше
.
2) Диагонали параллелограмма равны.
3) Любые две прямые имеют не менее одной общей точки.
4) Около всякого треугольника можно описать не более одной окружности.
Какие из следующих утверждений верны?
1) Если при пересечении двух прямых третьей прямой внутренние накрест лежащие углы
составляют в сумме
, то эти две прямые параллельны.
2) Площадь прямоугольного треугольника равна произведению его катетов.
3) Равнобедренный треугольник не имеет центра симметрии.
4) Равнобедренный треугольник не имеет осей симметрии.
Какие из следующих утверждений верны?
1) Центр окружности, вписанной в тупоугольный треугольник, находится вне этого
треугольника.
2) Около любой трапеции можно описать окружность.
3) Площадь треугольника не превосходит половины произведения двух его сторон на
синус угла между ними.
4) Стороны треугольника пропорциональны синусам прилежащих углов.
Какие из следующих утверждений верны?
1) Площадь круга равна четверти произведения длины его окружности на диаметр.
2) Прямая не имеет осей симметрии.
3) Сумма смежных углов равна
.
4) Если три угла одного треугольника соответственно равны трем углам другого
треугольника, то такие треугольники равны.
Какие из следующих утверждений верны?
1) Внешний угол треугольника больше каждого, не смежного с ним, внутреннего угла.
2) Равнобедренный треугольник не имеет осей симметрии.
3) Если дуга окружности составляет
равен
.
, то центральный угол, опирающийся на эту дугу,
4) Круг имеет одну ось симметрии.
Какие из следующих утверждений верны?
1) Любые два прямоугольных и равнобедренных треугольника подобны.
2) Если при пересечении двух прямых третьей прямой соответственные углы составляют в
сумме
, то эти две прямые параллельны.
3) Любые три прямые имеют не менее одной общей точки.
4) Ромб не имеет центра симметрии.
Какие из следующих утверждений верны?
1) Центр окружности, описанной около остроугольного треугольника, находится внутри
этого треугольника.
2) Если один из углов параллелограмма равен
.
, то противоположный ему угол равен
3) Если расстояние от точки до прямой больше 1, то и длина любой наклонной,
проведенной из данной точки к прямой, больше 1.
4) Прямая не имеет осей симметрии.
Какие из следующих утверждений верны?
1) В треугольнике против меньшего угла лежит большая сторона.
2) Около всякого треугольника можно описать не более одной окружности.
3) Центром симметрии правильного треугольника является точка пересечения его
биссектрис.
4) Если один из углов равнобедренного треугольника равен
равен
.
Какие из следующих утверждений верны?
1) Через любые три точки проходит не более одной окружности.
, то другой его угол
2) Если один угол треугольника больше
, то два других его угла меньше
.
3) Если катет и гипотенуза прямоугольного треугольника равны соответственно 6 и 10, то
второй катет этого треугольника равен 8.
4) Центр окружности, вписанной в тупоугольный треугольник, находится вне этого
треугольника.
Какие из следующих утверждений верны?
1) В равнобедренном треугольнике имеется не менее двух равных углов.
2) Квадрат любой стороны треугольника равен сумме квадратов двух других сторон без
произведения этих сторон на косинус угла между ними.
3) Центр окружности, описанной около тупоугольного треугольника, находится внутри
этого треугольника.
4) Правильный шестиугольник имеет три оси симметрии.
Какие из следующих утверждений верны?
1) Равнобедренный треугольник имеет единственную ось симметрии.
2) Диагонали параллелограмма делят его углы пополам.
3) В треугольнике
наименьшая.
, для которого
,
,
, сторона
4) Центр окружности, описанной около тупоугольного треугольника, находится вне этого
треугольника.
Какие из следующих утверждений верны?
1) Если радиус окружности равен 2, а расстояние от центра окружности до прямой равно
3, то эти прямая и окружность не имеют общих точек.
2) Площадь параллелограмма равна произведению двух его сторон на косинус угла
между ними.
3) Если расстояние от точки до прямой меньше 1, то и длина любой наклонной,
проведенной из данной точки к прямой, меньше 1.
4) Если катеты прямоугольного треугольника равны 5 и 12, то его гипотенуза равна 13.
Какие из следующих утверждений верны?
1) Квадрат любой стороны треугольника равен сумме квадратов двух других сторон без
произведения этих сторон на косинус угла между ними.
2) Через любые три точки проходит не более одной окружности.
3) Центром окружности, описанной около правильного треугольника является точка
пересечения высот.
4) Если сторона и угол одного треугольника соответственно равны стороне и углу
другого треугольника, то такие треугольники равны.
Какие из следующих утверждений верны?
1) Площадь трапеции меньше произведения суммы оснований на высоту.
2) Через любые три точки проходит не более одной окружности.
3) Площадь прямоугольного треугольника равна произведению его катетов.
4) Если катеты прямоугольного треугольника равны 5 и 12, то его гипотенуза равна 13.
Какие из следующих утверждений верны?
1) Сумма углов выпуклого четырехугольника больше
.
2) Диагонали квадрата делят его углы пополам.
3) Если две стороны и угол одного треугольника соответственно равны двум сторонам и
углу другого треугольника, то такие треугольники равны.
4) Если вписанный угол равен
равна
.
, то дуга окружности, на которую опирается этот угол,
Какие из следующих утверждений верны?
1) Правильный шестиугольник имеет центр симметрии.
2) В любой треугольник можно вписать не менее одной окружности.
3) Центром симметрии ромба является точка пересечения его диагоналей.
4) Если сторона треугольника равна 5, а высота, проведенная к этой стороне, равна 4, то
площадь этого треугольника равна 20.
Какие из следующих утверждений верны?
1) Если все стороны треугольника меньше 1, то и все его высоты меньше 1.
2) Если расстояние от точки до прямой больше 1, то и длина любой наклонной,
проведенной из данной точки к прямой, больше 1.
3) Если две стороны треугольника равны 4 и 5, а угол между ними равен
площадь этого треугольника равна 5.
4) Если дуга окружности составляет
окружности, равен
.
, то
, то вписанный угол, опирающийся на эту дугу
Какие из следующих утверждений верны?
1) Если два угла треугольника равны
и
, то третий угол равен
.
2) Через любые две точки проходит не менее одной окружности.
3) Около любого правильного многоугольника можно описать не более одной
окружности.
4) Если один угол треугольника больше
, то два других его угла меньше
.
В прямоугольном треугольнике один из катетов равен 20, а угол, лежащий напротив него,
равен
. Найдите площадь треугольника.
В прямоугольном треугольнике один из катетов равен 50, а угол, лежащий напротив него,
равен
. Найдите площадь треугольника.
В прямоугольном треугольнике один из катетов равен 88, а острый угол, прилежащий к
нему, равен
. Найдите площадь треугольника.
В прямоугольном треугольнике один из катетов равен 23, а угол, лежащий напротив него
равен
. Найдите площадь треугольника.
В прямоугольном треугольнике один из катетов равен 9, а острый угол, прилежащий к
нему, равен
. Найдите площадь треугольника.
В прямоугольном треугольнике гипотенуза равна 52, а один из острых углов равен
Найдите площадь треугольника.
.
В прямоугольном треугольнике гипотенуза равна 24, а один из острых углов равен
Найдите площадь треугольника.
.
В прямоугольном треугольнике гипотенуза равна 52, а один из острых углов равен
Найдите площадь треугольника.
.
Сторона равностороннего треугольника равна 48. Найдите его площадь.
Сторона равностороннего треугольника равна 16. Найдите его площадь.
Периметр равностороннего треугольника равен 264. Найдите его площадь.
Периметр равностороннего треугольника равен 114. Найдите его площадь.
Высота равностороннего треугольника равна 7. Найдите его площадь.
В равнобедренном треугольнике боковая сторона равна 94, а угол, лежащий напротив
основания, равен
. Найдите площадь треугольника.
В равнобедренном треугольнике боковая сторона равна 14, а угол, лежащий напротив
основания, равен
. Найдите площадь треугольника.
Периметр равнобедренного треугольника равен 48, а боковая сторона — 15. Найдите
площадь треугольника.
Периметр равнобедренного треугольника равен 196, а боковая сторона — 53. Найдите
площадь треугольника.
Периметр равнобедренного треугольника равен 324, а боковая сторона — 90. Найдите
площадь треугольника.
Периметр равнобедренного треугольника равен 392, а основание — 192. Найдите площадь
треугольника.
Периметр равнобедренного треугольника равен 98, а основание — 40. Найдите площадь
треугольника.
В треугольнике одна из сторон равна 27, а опущенная на нее высота — 11. Найдите
площадь треугольника.
В треугольнике одна из сторон равна 21, а опущенная на нее высота — 29. Найдите
площадь треугольника.
В треугольнике одна из сторон равна 2, а опущенная на нее высота — 17. Найдите
площадь треугольника.
В треугольнике одна из сторон равна 7, а опущенная на нее высота — 1. Найдите площадь
треугольника.
В треугольнике одна из сторон равна 2, другая равна
. Найдите площадь треугольника.
, а угол между ними равен
В треугольнике одна из сторон равна 16, другая равна
. Найдите площадь треугольника.
, а угол между ними равен
В треугольнике одна из сторон равна 12, другая равна
. Найдите площадь треугольника.
, а угол между ними равен
В треугольнике одна из сторон равна 28, другая равна
. Найдите площадь треугольника.
, а угол между ними равен
В треугольнике одна из сторон равна 18, другая равна
, а угол между ними равен
. Найдите площадь треугольника.
В треугольнике одна из сторон равна 19, другая равна 9, а угол между ними равен
Найдите площадь треугольника.
.
В треугольнике одна из сторон равна 50, другая равна 4, а синус угла между ними равен
. Найдите площадь треугольника.
В треугольнике одна из сторон равна 2, другая равна 1, а синус угла между ними равен
. Найдите площадь треугольника.
В треугольнике одна из сторон равна 16, другая равна 20, а синус угла между ними равен
. Найдите площадь треугольника.
В треугольнике одна из сторон равна 35, другая равна 17, а синус угла между ними равен
. Найдите площадь треугольника.
В треугольнике одна из сторон равна 50, другая равна 4, а косинус угла между ними равен
. Найдите площадь треугольника.
В треугольнике одна из сторон равна 10, другая равна 28, а косинус угла между ними
равен
. Найдите площадь треугольника.
В треугольнике одна из сторон равна 36, другая равна 26, а косинус угла между ними
равен
. Найдите площадь треугольника.
В треугольнике одна из сторон равна 20, другая равна 29, а тангенс угла между ними
равен
. Найдите площадь треугольника.
В треугольнике одна из сторон равна 60, другая равна 3, а тангенс угла между ними равен
. Найдите площадь треугольника.
Сторона квадрата равна 48. Найдите площадь квадрата.
Периметр квадрата равен 116. Найдите площадь квадрата.
Периметр квадрата равен 152. Найдите площадь квадрата.
В прямоугольнике одна сторона равна 10, другая сторона равна 14. Найдите площадь
прямоугольника.
В прямоугольнике одна сторона равна 1, другая сторона равна 17. Найдите площадь
прямоугольника.
В прямоугольнике одна сторона равна 13, другая сторона равна 9. Найдите площадь
прямоугольника.
В прямоугольнике одна сторона равна 13, периметр равен 62. Найдите площадь
прямоугольника.
В прямоугольнике одна сторона равна 14, периметр равен 54. Найдите площадь
прямоугольника.
В прямоугольнике диагональ равна 42, а угол между ней и одной из сторон равен
Найдите площадь прямоугольника.
Сторона ромба равна 29, а диагональ равна 42. Найдите площадь ромба.
Сторона ромба равна 73, а диагональ равна 110. Найдите площадь ромба.
Сторона ромба равна 95, а диагональ равна 114. Найдите площадь ромба.
Сторона ромба равна 90, а диагональ равна 144. Найдите площадь ромба.
Периметр ромба равен 148, а один из углов равен
. Найдите площадь ромба.
Периметр ромба равен 112, а один из углов равен
. Найдите площадь ромба.
Периметр ромба равен 184, а один из углов равен
. Найдите площадь ромба.
Периметр ромба равен 28, а один из углов равен
Периметр ромба равен 128, а один из углов равен
. Найдите площадь ромба.
. Найдите площадь ромба.
Периметр ромба равен 108, а синус одного из углов равен
Периметр ромба равен 36, а синус одного из углов равен
. Найдите площадь ромба.
. Найдите площадь ромба.
.
Периметр ромба равен 32, а синус одного из углов равен
. Найдите площадь ромба.
Периметр ромба равен 80, а косинус одного из углов равен
ромба.
. Найдите площадь
Периметр ромба равен 84, а косинус одного из углов равен
ромба.
. Найдите площадь
Периметр ромба равен 144, а косинус одного из углов равен
ромба.
. Найдите площадь
Периметр ромба равен 32, а тангенс одного из углов равен
ромба.
. Найдите площадь
Периметр ромба равен 72, а тангенс одного из углов равен
ромба.
. Найдите площадь
Периметр ромба равен 128, а тангенс одного из углов равен
Периметр ромба равен 20, а тангенс одного из углов равен
. Найдите площадь ромба.
. Найдите площадь ромба.
Одна из сторон параллелограмма равна 20, а опущенная на нее высота равна 23. Найдите
площадь параллелограмма.
Одна из сторон параллелограмма равна 16, а опущенная на нее высота равна 25. Найдите
площадь параллелограмма.
Одна из сторон параллелограмма равна 19, а опущенная на нее высота равна 27. Найдите
площадь параллелограмма.
Одна из сторон параллелограмма равна 13, другая равна 24, а один из углов —
Найдите площадь параллелограмма.
.
Одна из сторон параллелограмма равна 17, другая равна 10, а один из углов —
Найдите площадь параллелограмма.
.
Одна из сторон параллелограмма равна 30, другая равна 9, а один из углов —
.
Найдите площадь параллелограмма.
Одна из сторон параллелограмма равна 3, другая равна 5, а один из углов —
Найдите площадь параллелограмма.
.
Одна из сторон параллелограмма равна 6, другая равна 27, а один из углов —
Найдите площадь параллелограмма.
.
Одна из сторон параллелограмма равна 21, другая равна 3, а один из углов —
Найдите площадь параллелограмма.
.
Одна из сторон параллелограмма равна 1, другая равна 12, а один из углов —
Найдите площадь параллелограмма.
.
Одна из сторон параллелограмма равна 18, другая равна 25, а синус одного из углов равен
Найдите площадь параллелограмма.
Одна из сторон параллелограмма равна 45, другая равна 27, а синус одного из углов равен
. Найдите площадь параллелограмма.
Одна из сторон параллелограмма равна 24, другая равна 20, а синус одного из углов равен
. Найдите площадь параллелограмма.
Одна из сторон параллелограмма равна 50, другая равна 1, а косинус одного из углов
равен
. Найдите площадь параллелограмма.
Одна из сторон параллелограмма равна 4, другая равна 4, а косинус одного из углов равен
. Найдите площадь параллелограмма.
Одна из сторон параллелограмма равна 21, другая равна 15, а косинус одного из углов
равен
. Найдите площадь параллелограмма.
Одна из сторон параллелограмма равна 8, другая равна 18, а тангенс одного из углов равен
. Найдите площадь параллелограмма.
Одна из сторон параллелограмма равна 20, другая равна 29, а тангенс одного из углов
равен
. Найдите площадь параллелограмма.
.
Одна из сторон параллелограмма равна 15, другая равна 6, а тангенс одного из углов равен
. Найдите площадь параллелограмма.
Одна из сторон параллелограмма равна 9, другая равна 22, а тангенс одного из углов равен
. Найдите площадь параллелограмма.
Основания трапеции равны 4 и 25, одна из боковых сторон равна
и одним из оснований равен
. Найдите площадь трапеции.
, а угол между ней
Основания трапеции равны 16 и 18, одна из боковых сторон равна
и одним из оснований равен
. Найдите площадь трапеции.
, а угол между ней
Основания трапеции равны 21 и 22, одна из боковых сторон равна
и одним из оснований равен
. Найдите площадь трапеции.
, а угол между ней
Основания трапеции равны 4 и 12, одна из боковых сторон равна
и одним из оснований равен
. Найдите площадь трапеции.
, а угол между ней
Основания трапеции равны 9 и 24, одна из боковых сторон равна
одним из оснований равен
. Найдите площадь трапеции.
, а угол между ней и
Основания трапеции равны 1 и 17, одна из боковых сторон равна
и одним из оснований равен
. Найдите площадь трапеции.
, а угол между ней
Основания трапеции равны 5 и 45, одна из боковых сторон равна 13, а синус угла между
ней и одним из оснований равен
. Найдите площадь трапеции.
Основания трапеции равны 10 и 110, одна из боковых сторон равна 8, а синус угла между
ней и одним из оснований равен
. Найдите площадь трапеции.
Основания трапеции равны 10 и 100, одна из боковых сторон равна 5, а синус угла между
ней и одним из оснований равен
. Найдите площадь трапеции.
Основания трапеции равны 3 и 12, одна из боковых сторон равна 3, а синус угла между
ней и одним из оснований равен
. Найдите площадь трапеции.
Основания трапеции равны 7 и 42, одна из боковых сторон равна 15, а косинус угла между
ней и одним из оснований равен
. Найдите площадь трапеции.
Основания трапеции равны 7 и 56, одна из боковых сторон равна 21, а косинус угла между
ней и одним из оснований равен
. Найдите площадь трапеции.
Основания трапеции равны 9 и 27, одна из боковых сторон равна 26, а косинус угла между
ней и одним из оснований равен
. Найдите площадь трапеции.
Основания трапеции равны 3 и 24, одна из боковых сторон равна 7, а тангенс угла между
ней и одним из оснований равен
. Найдите площадь трапеции.
Основания трапеции равны 2 и 16, одна из боковых сторон равна 6, а тангенс угла между
ней и одним из оснований равен
. Найдите площадь трапеции.
Основания трапеции равны 9 и 45, одна из боковых сторон равна 25, а тангенс угла между
ней и одним из оснований равен
. Найдите площадь трапеции.
Радиус круга равен 41. Найдите его площадь.
Радиус круга равен 14. Найдите его площадь.
Найдите площадь кругового сектора, если радиус круга равен 4, а угол сектора равен
.
Найдите площадь кругового сектора, если радиус круга равен 3,6, а угол сектора равен
.
Найдите площадь кругового сектора, если длина ограничивающей его дуги равна
угол сектора равен
.
,а
В прямоугольном треугольнике один из катетов равен 43, острый угол, прилежащий к
нему, равен
, а гипотенуза равна 86. Найдите площадь треугольника.
В прямоугольном треугольнике один из катетов равен 5, острый угол, прилежащий к
нему, равен
, а гипотенуза равна 10. Найдите площадь треугольника.
В прямоугольном треугольнике один из катетов равен
, острый угол, прилежащий к
нему, равен
, а гипотенуза равна 28. Найдите площадь треугольника.
В прямоугольном треугольнике один из катетов равен
, острый угол, прилежащий к
нему, равен
, а гипотенуза равна 64. Найдите площадь треугольника.
В прямоугольном треугольнике один из катетов равен 4, угол, лежащий напротив него,
равен
, а гипотенуза равна 8. Найдите площадь треугольника.
В прямоугольном треугольнике один из катетов равен
, угол, лежащий напротив
него, равен
, а гипотенуза равна 34. Найдите площадь треугольника.
В прямоугольном треугольнике один из катетов равен
, угол, лежащий напротив
него, равен
, а гипотенуза равна 98. Найдите площадь треугольника.
В равнобедренном треугольнике боковая сторона равна 47, основание —
лежащий напротив основания, равен
. Найдите площадь треугольника.
, а угол,
В равнобедренном треугольнике боковая сторона равна 17, основание —
лежащий напротив основания, равен
. Найдите площадь треугольника.
, а угол,
В прямоугольнике диагональ равна 96, угол между ней и одной из сторон равен
длина этой стороны
. Найдите площадь прямоугольника.
,
В прямоугольнике диагональ равна 92, а угол между ней и одной из сторон равен
длина этой стороны равна 46. Найдите площадь прямоугольника.
,
В прямоугольнике диагональ равна 4, а угол между ней и одной из сторон равен
длина этой стороны равна 2. Найдите площадь прямоугольника.
,
В ромбе сторона равна 38, одна из диагоналей —
диагонали, равен
. Найдите площадь ромба.
, а угол, лежащий напротив этой
В ромбе сторона равна 33, одна из диагоналей —
диагонали, равен
. Найдите площадь ромба.
, а угол, лежащий напротив этой
В ромбе сторона равна 68, одна из диагоналей — 68, а угол, лежащий напротив этой
диагонали, равен
. Найдите площадь ромба.
В ромбе сторона равна 22, одна из диагоналей —
диагональ, равен
. Найдите площадь ромба.
, а угол, из которого выходит эта
В ромбе сторона равна 16, одна из диагоналей —
диагональ, равен
. Найдите площадь ромба.
, а угол, из которого выходит эта
В ромбе сторона равна 44, одна из диагоналей — 44, а угол, из которого выходит эта
диагональ, равен
. Найдите площадь ромба.
В ромбе сторона равна 54, одна из диагоналей — 54, а угол, из которого выходит эта
диагональ, равен
. Найдите площадь ромба.
Радиус круга равен 36, а длина ограничивающей его окружности равна
площадь круга.
. Найдите
Найдите площадь кругового сектора, если длина ограничивающей его дуги равна
угол сектора равен
, а радиус круга равен 2.
,
Найдите площадь кругового сектора, если длина ограничивающей его дуги равна
угол сектора равен
, а радиус круга равен 7,5.
,