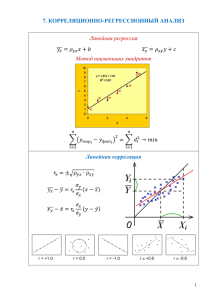
§4.1. Линейная корреляционная зависимость

§4.1. Линейная корреляционная зависимость
Часто на практике требуется установить вид и оценить силу
зависимости изучаемой случайной величины Y от одной или
нескольких других величин (случайных или неслучайных). Рассмотрим
сначала зависимость случайной величины Y от одной случайной X.
Две величины могут быть связаны:
1) функциональной зависимостью (Y=f(X)), либо 2) статистической
зависимостью.
Статистическая зависимость – зависимость, при которой изменение
одной из величин влечет изменение распределения другой (вида
распределения, либо числовых характеристик распределения).
Корреляционная зависимость – статистическая зависимость, при
которой изменение одной из величин влечет изменение среднего
значения другой. С математической точки зрения корреляционная
зависимость – функциональная зависимость условного среднего y x от
x:
y x = f (x ),
(1)
где y x - выборочное условное среднее ( среднее арифметическое
значений Y, соответствующих значению x величины X); уравнение (1)
называют выборочным уравнением регрессии Y на X; f ( x ) выборочная функция регрессии Y на X; график функции f ( x )
называют линией регрессии Y на X. Аналогично, x y - условное среднее
X на Y; x y = ϕ ( y ) - выборочное уравнение регрессии X на Y; ϕ ( y ) функция регрессии X на Y; график функции ϕ ( y ) называют линией
регрессии X на Y.
Задачи теории корреляции
Теория корреляции решает следующие задачи:
1) Установление формы корреляционной зависимости, т.е. вида
функций f ( x ), ϕ ( y ) (если обе функции f ( x ), ϕ ( y ) являются линейными,
то корреляционная зависимость называется линейной; в противном
случае – нелинейной корреляционной зависимостью);
2) Оценка силы (тесноты) корреляционной зависимости.
Пусть в результате независимых испытаний получено n пар значений
(xi , y i ) . Предположим, что X и Y связаны линейной корреляционной
зависимостью, т.е.
.
Найдем по выборочным значениям ( xi , y i ) точечные оценки
так, чтобы
точки ( xi , y i ) , построенные на
параметров
координатной плоскости, находились вблизи прямой
(1)
Метод наименьших квадратов
Выборочные параметры
минимум функции
(
)
находят из условия обращения в
n
n
i =1
i =1
(
Q b yx , b = ∑ ( f ( xi ) − y i )2 = ∑ b yx xi + b − y i
)2
Для отыскания минимума функции
приравняем нули соответствующие частные производные
(2)
Выполняя элементарные преобразования, получим систему двух
линейных уравнений относительно
(3)
1 n
1 n
1 n 2
2
∑ xi , y = ∑ yi , x = ∑ xi , ni j - число наблюдений одной и
n i =1
n i =1
n i =1
той же пары значений ( xi , y i ) , k- число различных пар ( xi , y i ) . Из
системы уравнений (3) следует, что
где x =
При этом выборочное уравнение регрессии Y на X примет вид
yx − y = r
где
Sy
Sx
(x − x ),
- выборочный коэффициент корреляции. Аналогично
уравнение регрессии X на Y имеет вид
S
x y − x = r x ( y − y ) , где
Sy
.
Пример. При большом числе наблюдений одно и то же значение
х может встретиться n x раз, одно и то же значение y может
встретиться n y раз, одна и та же пара значений чисел (x,y) может
наблюдаться n xy раз. Поэтому данные наблюдений группируют, т.е.
подсчитывают n x , n y , n xy . Все сгруппированные данные записывают
в виде таблицы, которую называют корреляционной.
X
Y
15
10
20
5
7
25
30
40
50
60
ny
12
20
23
43
35
30
47
2
45
10
11
20
6
47
9
7
3
19
67
29
9
n = 200
55
nx
5
27
63
79
В первой строке таблицы указаны наблюдаемые значения величины X,
а в первом столбце – наблюдаемые значения величины Y. На
пересечении строк и столбцов вписаны частоты n xy наблюдаемых пар
значений этих величин. Например, частота 5 указывает, что пара чисел
(10,15) наблюдалась 5 раз. В последнем столбце записаны суммы
частот строк. В последней строке записаны суммы частот столбцов.
Вычислим выборочный коэффициент корреляции по данным
корреляционной таблицы. Можно значительно упростить вычисления,
x −c
y − c2
, переход к
если перейти к условным вариантам ui = i 1 , vi = i
h1
h2
которым не меняет величины выборочного коэффициента корреляции
r=
∑ n xy xy − nx y
nS x S y
n uv − nu v
= ∑ uv
nSu Sv
xi − c1 xi − 40
=
, где в качестве нуля c1 взята
10
h1
варианта x = 40 , имеющая наибольшую частоту 47; шаг h1 равен
разности между двумя соседними вариантами. Условные варианты
y −c
y − 35
vi = i 2 = i
, где в качестве нуля c2 взята варианта y = 35 ,
10
h2
имеющая наибольшую частоту 47; шаг h2 равен разности между двумя
В данном примере ui =
u
v
-2
-3
-2
5
7
-1
-1
0
1
2
nv
12
20
23
43
0
30
47
2
1
10
11
20
6
47
9
7
3
19
67
29
9
n = 200
2
5
nu
27
63
79
соседними вариантами. Составим корреляционную таблицу в условных
вариантах. Практически это делается так: в первом столбце вместо
варианты 35, имеющей наибольшую частоту, пишут 0; над нулем
пишут последовательно –1,-2…; под нулем пишут 1,2…. В первой
строке вместо варианты 40, имеющей наибольшую частоту, пишут 0;
слева от нуля последовательно пишут –1,-2….; справа от нуля пишут
1,2…. Все остальные данные переписывают из первоначальной
корреляционной таблицы. В итоге получим корреляционную таблицу в
условных вариантах.
Найдем u и v
∑ nu u = 5 ⋅ ( −3) + 27 ⋅ ( −2) + 63 ⋅ ( −1) + 29 ⋅ 1 + 9 ⋅ 2 = −0.425,
u=
v=
n
∑ nv v
n
200
12 ⋅ (− 2 ) + 43 ⋅ (− 1) + 47 + 19 ⋅ 2
=
= 0.090
200
Вычислим вспомогательную величину u 2 , а затем S u :
nu u 2 5 ⋅ 9 + 27 ⋅ 4 + 1 ⋅ 63 + 1 ⋅ 29 + 9 ⋅ 4
∑
u =
=
= 1.405
2
n
200
Su = u 2 − u 2 = 1.405 − 0.4252 = 1.106
Аналогично получим S v = 1.209 .
Найдем ∑ nuv uv метод 4 полей, для чего составим расчетную таблицу
U
1
2
1
20
6
2
7
3
V
-2
-1
-3
-2
5
7
20
-1
0
23
0
I
30
III
68
23
II
-10
IV
34
24
Название метода связано с тем, что строка и столбец, пересекающиеся
в клетке, содержащей наибольшую частоту, делят корреляционную
таблицу на 4 части, которые называют полями. Поле нумеруется так,
как указано в таблице.
Найдем произведения пар вариант u и v и поместим их в верхние
правые углы клеток, содержащих соответствующие частоты. Заполнив
подобным образом остальные клетки 1,2,3,4 полей, получим таблицу,
приведенную выше. Сложив числа итоговых клеток, получим
∑ nuv uv = 121 − 10 + 58 = 169 . Найдем искомый коэффициент корреляции
n uv − n u v 169 − 200(− 0.425) ⋅ 0.09
=
= 0.603
r = ∑ uv
200 ⋅ 1.106 ⋅ 1.209
n Su S v
Теперь, когда известно как вычисляют r уместно привести пример на
отыскание уравнения прямой линии регрессии. Поскольку при
нахождении r уже вычислены u , v , Su , S v , то для нахождения
x , y , S x , S y целесообразно вывести формулы, связывающие
u , v , Su , Sv и x , y , S x , S y . Выведем эти формулы
1 n
1 n ⎛ x −c ⎞ x c
u = ∑ ui = ∑ ⎜⎜ i 1 ⎟⎟ = − 1 , так что x = u h1 + c1 . Аналогично
n i =1
n i =1⎝ h1 ⎠ h1 h1
y = v h2 + c2 .
2
Тогда
Su =
1` n ⎛ xi − c1 x − c1 ⎞
1
1 n
S
⎟⎟ =
−
∑ ⎜⎜
∑ ( xi − x )2 = x ,
n − 1 i =1⎝ h1
h1 ⎠
h1 n − 1 i =1
h1
так что S x = h1Su . Аналогично S y = h2 Sv . Итак
x = u h1 + c1 , y = v h2 + c2 , S x = h1Su , S y = h2 S x
Запишем искомое уравнение в общем виде
yx − y = r
Sy
Sx
(x − x )
(4)
Коэффициент корреляции уже ранее вычислен и равен r = 0.603.
Остается найти x , y , S x , S y :
x = u h1 + c1 = −0.425 ⋅ 10 + 40 = 35.75
y = v h2 + c2 = 0.09 ⋅ 10 + 35 = 35.9
S x = Su h1 = 1.106 ⋅ 10 = 11.06
(5)
S y = Sv h2 = 1.209 ⋅ 10 = 12.09
Подставляя (5) в (4), получим искомое уравнение
12.09
(x − 35.75)
y x − 35.9 = 0.603 ⋅
11.06
или окончательно
y x = 0.659 ⋅ x + 12.34
(6)
Сравним условные средние, вычисленные по уравнению (6) и по
данным корреляционной таблицы. Например, при x=30: по уравнению
(6) получим
y30 = 0.659 ⋅ 30 + 12.34 = 32.11,
23 ⋅ 25 + 30 ⋅ 35 + 10 ⋅ 45
а по таблице y30 =
= 32.94.
63
Как видим, согласование расчетного (согласно (6)) и
наблюдаемого условных средних – удовлетворительное.
Доверительные оценки параметров прямой регрессии y на x .
При
нахождении доверительного интервала для оценки
теоретической прямой линии регрессии y на x
параметров
используется сумма квадратов отклонений измеренных значений yi от
рассчитанных по выборочному уравнению прямой линии регрессии:
2
(
)
Sy
⎡
⎤
Q = ∑ ⎢ yi − r ( xi − x )⎥ = (n − 1) 1 − r 2 S 2y .
Sx
⎦
i =1⎣
n
При этом предполагается, что все ошибки измерения независимы и
одинаково распределены по нормальному закону с центром 0 и
дисперсией σ 2 .
Границы доверительного интервала для параметра равны
а границами доверительного интервала для параметра
служат
где коэффициент t берется из таблицы распределения Стьюдента при
числе степеней свободы k = n − 2 .
Доверительный интервал для оценки отклонения теоретической
прямой линии регрессии от эмпирической
При фиксированном значении x = x0 границы доверительного
интервала для теоретической прямой регрессии определяются
формулами
t
n ( x0 − x )2
,
yt ( x0 ) = ye ( x0 ) ±
1+
n−2
(n − 1) S x2
здесь
, коэффициент t берется из таблицы
распределения Стьюдента при числе степеней свободы k = n − 2 .
Следует помнить, что эта оценка значительно ухудшается по мере
удаления от среднего значения x .
Например, для вышеприведенного примера t (0.95,198 ) = 1.96 и
соответственно границы доверительного интервала для x0 = 30 равны
32.11 ± 1.30 , так что наблюдаемое среднее y30 = 32.94 принадлежит
доверительному интервалу.
Свойства выборочного коэффициента корреляции
Выведем формулы
( )
⋅ (1 − r )
S y2x = S y2 ⋅ 1 − r 2
(1)
S x2y = S x2
(2)
2
Для этого предположим, что величины Y и X связаны линейной
корреляционной зависимостью
yx = α + β x
Тогда получим
S y2x =
=
∑ ( yi − y x )
∑ [ y i − α − β xi ]
∑ [( y i − y ) − β ( xi − x ) + ( y − β x − α )]
=
=
=
2
2
n
∑ ( yi − y )
2
2
n
+β2
∑ ( xi − x )
2
n
+ ( y − β x − α )2 − 2 β
∑ ( y i − y ) ⋅ ( xi − x )
+
n
n
∑ ( yi − y )
∑ ( xi − x )
+ 2(y − β x −α )
+ 2(y − β x − α )
= S y2 + β 2 S x2 + ( y − β x − α )2 −
n
n
∑ xy − n ⋅ x ⋅ y
− 2β
n
n
Итак, окончательно имеем
S y2x = S y2 + β 2 S x2 + ( y − β x − α )2 − 2 β
∑ xy − nx ⋅ y
(3)
n
Параметры α , β найдем из условия минимума функции S y2x (α , β ) .
Необходимые условия минимума этой функции имеют вид
∂S y2x
= −2( y − β x − α ) = 0
∂α
∂ S y2x
= 2 β S x2 − 2 x ( y − β x − α ) − 2
∑ xy − n x y
∂β
Из уравнения (5) находим
β=
∑ xy − n x y
nS x2
=r
n
(4)
=0
(5)
Sy
(6)
Sx
Из уравнения (4) следует
α = −y + β x = −y + r
Sy
Sx
(7)
x
(
)
Подставляя (6) и (7) в (3), получим формулу (1) S y2x = S y2 ⋅ 1 − r 2 .
(
)
Аналогично S x2y = S x2 ⋅ 1 − r 2 .
Свойство 1. Выборочный коэффициент корреляции по модулю не
превосходит единицу − 1 ≤ r ≤ 1 .
Доказательство
Так как любая дисперсия неотрицательна, т.е. S y2x ≥ 0, S y2 ≥ 0 , то из
(
формулы S y2x = S y2 ⋅ 1 − r 2
)
следует, что r 2 ≤ 1 или − 1 ≤ r ≤ 1 , что и
требовалось показать.
Свойство 2. Если r = 0 , то наблюдаемые значения x, y не связаны
линейной корреляционной зависимостью.
Доказательство
Доказательство проведем по методу от противного. Предположим,
что наблюдаемые значения x, y связаны линейной корреляционной
зависимостью, т.е.
y x = y + b yx (x − x )
x y = x + bxy ( y − y )
y x = y , x y = x , что противоречит
Отсюда при r = 0 следует
предположению.
Замечание. Если r = 0 , то x, y могут быть связаны нелинейной
корреляционной
зависимостью
или
даже
функциональной
зависимостью.
Свойство 3. Если r = 1, то наблюдаемые значения x, y связаны
линейной функциональной зависимостью.
Доказательство
При
из
формулы
следует,
что
r =1
S y2x = S y2 ⋅ 1 − r 2
(
S y2x
)
∑ ( yi − y x )
=
= 0 , т.е. yi = y x . Тогда из y x = y + b yx (x − x ) следует
2
n
yi = y + b yx ( xi − x ) ,
что и требовалось доказать.
Замечание. Из свойства (3) следует, что только наблюдаемые
значения, а не
все возможные значения связаны линейной
функциональной зависимостью.
Из доказанных свойств следует, что r характеризует силу линейной
корреляционной зависимости между количественными признаками в
выборке:
1) чем ближе r к единице, тем связь сильнее;
2) чем ближе r к нулю, тем связь слабее.
Замечание. Если выборка имеет достаточно большой объем, то
заключение о силе линейной корреляционной зависимости между
наблюдаемыми значениями признаков может быть распространена на
всю совокупность значений признаков X и Y.
§4.2. Выборочное корреляционное отношение
Для оценки тесноты линейной корреляционной связи между
физическими величинами в выборке служит выборочный коэффициент
корреляции r. Для оценки тесноты любой корреляционной связи вводят
другие характеристики.
Пусть данные наблюдений за количественными признаками X и
Y сведены в корреляционную таблицу. Тем самым наблюдаемые
значения Y оказываются разбиты на группы; каждая группа содержит
те значения Y, которые соответствуют определенному значению X. Так
как все значения признака Y разбиты на группы, то можно представить
Dобщ = Dвнгр + D межгр
(1)
При этом оказывается справедливым следующее утверждение.
Утверждение12. 1)Если величина
функциональной зависимостью, то
D межгр
=1
Dобщ
Y связана
с величиной X
2)если
величина Y связана с величиной X корреляционной
зависимостью, то
D межгр
<1
Dобщ
Докажем это утверждение. Доказательство разобьем на две части.
Сначала докажем первую часть утверждения.
1) Если случайная величина Y связана с случайной величиной X
функционально, то по определению функциональной зависимости
определенному значению x соответствует только одно значение y.
Поэтому в каждой j группе ее элементы равны между собой, т.е.
(2)
y1 j = y 2 j = ...... = y ∗j
Из (2) следует, что групповое среднее
y ∗j m j
1 mj
1 mj
∗
∗
yj =
(3)
∑ ni j yi j =
∑ ni j y j =
∑ ni j = y j
N j i =1
N j i =1
N j i =1
Следовательно, групповая дисперсия равна
1 mj
1 mj
2
∗
∗
Dj =
∑ ni j yi j − y j =
∑ ni j y j − y j
N j i =1
N j i =1
(
)
(
)
2
=0
(4)
В свою очередь, из (4) вытекает, что
1 k
(5)
Dвнгр = ∑ N j D j = 0
n j =1
Подставляя (5) в (1), получим
Dобщ = D межгр
D межгр
= 1, что и требовалось показать в первой
Отсюда находим
Dобщ
части.
2) Если случайная величина Y связана с случайной величиной X
корреляционной зависимостью, то определенному значению x
соответствуют, вообще говоря, различные значения yi j , образующие
группу. Поэтому в этом случае D j ≠ 0 . Следовательно, Dвнгр ≠ 0 . Так
как
то D межгр < D межгр + Dвнгр , т.е. согласно (1)
D межгр
< 1 , что и требовалось показать во
< Dобщ , так что
Dобщ
Dвнгр > 0, D межгр ≥ 0 ,
D межгр
второй части.
Из доказанного утверждения видно, что чем связь между
величинами ближе к функциональной, тем больше будет приближаться
D межгр
к единице отношение
. Отсюда ясно, что целесообразно
Dобщ
рассматривать в качестве меры тесноты корреляционной зависимости
D межгр
отношение
или, что то же, отношение
Dобщ
Выборочным корреляционным отношением Y к X называют
отношение вида
где
,
n – объем выборки, n x - частота значения x случайной величины X; n y
- частота значения y случайной величины Y; y - общее среднее
величины Y; y x - групповое среднее величины Y. Аналогично
определяется выборочное корреляционное отношение X к Y
Пример. По данным корреляционной таблицы вычислим η yx .
X
10
20
30
ny
xy
15
4
28
6
38
20.5
25
6
6
12
20
nx
10
28
12
n=50
yx
21
15
20
Y
Найдем общее среднее
1
38 ⋅15 + 12 ⋅ 25
= 17.4
∑ ny y =
50
n
Вычислим выборочные средние квадратичные отклонения
y=
Тогда выборочное корреляционное отношение равно
Аналогично
x=
x25
1
10 ⋅10 + 28 ⋅ 20 + 12 ⋅ 30
4 ⋅10 + 28 ⋅ 20 + 6 ⋅ 30
= 20.4, x15 =
= 20.53
∑ nx x =
n
50
38
6 ⋅ 10 + 6 ⋅ 30
=
= 20
12
Видим, что, вообще говоря, η yx ≠ η xy .
Вычислим теперь выборочный коэффициент корреляции r и
сравним его с корреляционным отношением η . Для этого перейдем к
условным вариантам
x − 20
y − 15
, vi = i
ui = i
10
10
Перепишем в условных координатах корреляционную таблицу
-1
0
1
V
0
U
nv
4
28
6
38
1
6
6
12
nu
10
12
n=50
28
Вычислим значение выборочного коэффициента корреляции
∑ nuv uv − n u v
r=
n σ uσ v
Для этого найдем соответствующие средние значения
u=
− 1 ⋅10 + 0 ⋅ 28 + 1 ⋅12 2
0 ⋅ 38 + 1 ⋅12 12 2 22 2 12
= ,v=
= ,u = ,v =
50
50
50
50
50
50
Найдем выборочные средние отклонения
1096
1056
, σ v = v2 − v 2 =
σu = u2 − u 2 =
50
50
Вычислим сумму ∑ nuv uv = 4 ⋅ 0 + 6 ⋅ (− 1) + 1 ⋅ 0 ⋅ 6 + 1 ⋅1 ⋅ 6 = 0 .
значение выборочного коэффициента корреляции равно
2 ⋅12
uv
= − 0.02
r=−
=−
σuσv
1096 1056
⋅
50 ⋅ 50 ⋅
50
50
В данном примере η > r . Это соотношение является общим.
Тогда
Свойства выборочного корреляционного отношения
Так как η yx обладает теми же свойствами, что и η xy , то
рассмотрим свойства только η yx , которое для упрощения записи
обозначим через η и будем называть корреляционным отношением.
0 ≤η ≤1
Доказательство
Так как по определению D межгр ≥ 0, Dобщ ≥ 0 , то
Свойство 1.
Следовательно, η ≥ 0 . Из соотношения
Dобщ = D межгр + Dвнгр
следует, что
Dвнгр D межгр
Dвнгр
+
= 1 или
+η2 = 1
Dобщ
Dобщ
Dобщ
Dвнгр
≥ 0, η 2 ≥ 0 , то каждое из слагаемых ≤ 1 ; в частности,
Так как
Dобщ
η 2 ≤ 1 . Приняв во внимание, что η ≥ 0 , заключаем 0 ≤ η ≤ 1, что и
требовалось показать.
Свойство 2. Если η = 0 , то Y и X корреляционной зависимостью
не связаны.
Доказательство
следует, что
и, следовательно, D межгр = 0 .
Из
Равенство D межгр = 0 означает, что y x = y , т.е. при всех значениях
случайной величины X y x сохраняет постоянное значение, равное
y . Иными словами, при η = 0 условное среднее y x не является
функцией от x, а значит, величина Y не связана корреляционной
зависимостью с величиной X. Верно и обратное утверждение: если
y x = const , т.е. y x1 = y x2 = ..... = y , то D межгр = 0 и, следовательно,
, η = 0.
Свойство 3. Если η = 1 , то Y и X связаны функционально.
Из η = 1 следует, что
Доказательство
, D межгр
Так
как
Dобщ = D межгр + Dвнгр ,
то
= Dобщ
из
(1)
(1)
вытекает,
что
Dвнгр = 0 ⇒ D j = 0 , так что в каждой группе содержатся равные
значения yi j , т.е. каждому значению x соответствует одно значение y.
Поэтому величины Y и X связаны функционально. Верно и обратное
, η = 1.
утверждение: если y xi = yi , то и
Свойство 4. Всегда корреляционное отношение не меньше
коэффициента корреляции η ≥ r .
Свойство 5. Если η = r , то имеет место точная линейная
зависимость. Другими словами, если η = r , то точки ( xi , yi ) лежат на
прямой линии регрессии, найденной способом наименьших квадратов.
Убедимся, что
с возрастанием η корреляционная связь
становится
более
тесной.
Для
этого
преобразуем
соотношение Dобщ = D межгр + Dвнгр следующим образом
⎛ D межгр ⎞
⎟ = Dобщ ⋅ 1 − η 2
Dвнгр = Dобщ ⋅ ⎜1 −
⎜
Dобщ ⎟⎠
⎝
Из (2) видно, что при η → 1
Dвнгр → 0
Из (3) вытекает, что
Dj → 0
(
)
(2)
(3)
(4)
Из (4) следует, что yi j → y j , т.е. при η → 1 связь величин Y,X
становится более тесной, переходя в функциональную при η = 1
Поскольку в приведенных рассуждениях не делалось никаких
допущений о форме корреляционной связи, то η может служить мерой
тесноты корреляционной связи любой формы. В этом состоит
преимущество корреляционного отношения перед коэффициентом
корреляции, который оценивает тесноту лишь линейной связи.
Недостаток: η не позволяет судить, насколько близко
расположены точки, найденные по данным наблюдений, к кривой
определенного вида, например, к параболе, гиперболе и т.д.
§4.3. Нелинейная корреляционная зависимость
Если график функций регрессии f ( x ), ϕ ( y ) изображается кривой
линией, то корреляцию называют криволинейной. Например, функции
регрессии Y на X могут иметь вид:
y x = ax 2 + bx + c (параболическая корреляция второго
порядка)
(параболическая корреляция 3
y x = ax 3 + bx 2 + cx + d
порядка)
a
y x = + b (гиперболическая корреляция)
x
Теория криволинейной корреляции решает те же задачи, что и
теория линейной корреляции:
1) установление формы корреляционной связи;
2) установление тесноты корреляционной связи.
Неизвестные параметры уравнения регрессии ищут методом
наименьших квадратов. Для оценки тесноты криволинейной
корреляции служит выборочное корреляционное отношение.
Чтобы выяснить суть дела, ограничимся параболической
корреляцией 2 порядка, предположив, что данные n наблюдений
позволяют считать, что имеет место именно такая корреляция. В этом
случае выборочное уравнение регрессии Y на X имеет вид:
(1)
y x = Ax 2 + Bx + C ,
где А,В,С – неизвестные параметры, подлежащие определению.
Пользуясь методом наименьших квадратов, нетрудно получить
систему линейных уравнений относительно этих параметров:
⎧ A ∑ nx x 4 + B ∑ nx x3 + C ∑ nx x 2 = ∑ nx y x x 2
⎪⎪
3
2
(2)
⎨ A ∑ nx x + B ∑ nx x + C ∑ nx x = ∑ nx y x x
⎪
2
⎪⎩ A ∑ n x x + B ∑ n x x + C n = ∑ n x y x
Найденные из системы (2) параметры А,В,С подставляют в (1) и в
итоге получают искомое уравнение регрессии.
Пример. По данным корреляционной таблицы найдем выборочное
уравнение регрессии Y на X вида y x = Ax 2 + Bx + C :
X
Y
6
7
7.5
1
1.1
8
9
23
1
33
9
9
6.74
7.5
8
nx
yx
6 ⋅8
=6
8
1.2
ny
17
23
10
n=50
Составим расчетную таблицу
x
nx
1.0
8
1.1
yx
nx x
nx x 2
nx x3
nx x 4
nx y x
nx y x x
nx y x x 2
6
8
8
8
8
48
48
48
33
6.74
36.3
39.93
43.93
48.32
222.5
244.66
269.13
1.2
9
7.5
10.8
12.96
15.55
18.66
67.50
81
97.20
∑
50
55.1
60.89
67.48
74.98
338
373.66
414.33
Подставив числа нижней строки этой таблицы в (2), получим систему
⎧74.98 A + 67.48 B + 60.89C = 414.33
⎪
⎨67.48 A + 60.89 B + 55.10C = 373.66
⎪60.89 A + 55.10 B + 50C = 338
⎩
A = 1.95, B = 2.98, C = 1.10 , так что
Решив эту систему, найдем
искомое уравнение регрессии имеет вид
y x = 1.95 ⋅ x 2 + 2.98 ⋅ x + 1.10
При x=1 по исходной таблице y1 = 6 , а по уравнению (3) y1 = 6.03 .
(3)
§4.4. Множественная корреляционная зависимость
Ранее мы
рассматривали корреляционную связь между 2
величинами. Если исследуется связь между несколькими величинами,
то корреляцию называют множественной. Рассмотрим случай, когда
число величин равно 3 и связь между ними линейная
(z − z ) = A (x − x ) + B ( y − y )
В этом случае возникают задачи:
1) найти коэффициенты регрессии А,В;
2) оценить силу связи между величиной Z и обоими величинами
X,Y;
3) оценить силу связи между Z и X, Z и Y.
Первая задача решается методом наименьших квадратов:
σ x ryz − rxz rxy
σ rxz − ryz rxy
A= z
B
=
,
,
σ x 1 − rxy2
σ y 1 − rxy2
где rxz - коэффициент корреляции между X и Z; ryz - Y и Z; rxy - X и Y;
σ x , σ y ,σ z - выборочные средние квадратичные отклонения. Сила связи
величины Z с величинами X,Y оценивается выборочным совокупным
коэффициентом корреляции
rxz2 + ryz2 − 2rxy rxz ryz
R=
1 − rxy2
Сила связи между Z и X оценивается частным выборочным
коэффициентом корреляции
rxz ( y ) =
rxz − rxy ryz
(1 − r )(1 − r )
2
xy
2
yz
Сила же связи между Z и Y оценивается частным выборочным
коэффициентом корреляции
ryz ( x ) =
ryz − rxy rxz
(1 − r )(1 − r )
2
xy
2
xz
Эти коэффициенты имеют те же свойства и тот же смысл, что и
обыкновенный выборочный коэффициент корреляции, т.е. служат для
оценки линейной связи между величинами.
§4.5. Сглаживание
Часто экспериментальные данные представляют собой
зависимость величины f от некоторой другой величины x .
Измеренные с некоторой погрешностью или зашумленные
экспериментальные данные перед их анализом обычно сглаживают.
Если количество экспериментальных точек велико, то подбор
эмпирической формулы может оказаться весьма затруднительным:
формулы с малым числом параметров могут давать большие
искажения, а большое число параметров неудобно для анализа. С
другой стороны, многие задачи анализа (например, связанные с
дифференцированием или интегрированием) не требуют единой
аналитической формулы для всех данных. Для анализа важно лишь
устранить «шум» эксперимента, сохранив информацию об истинной
функции.
Для этой цели применяется сглаживание эмпирических данных,
т.е. замена данной таблицы опытных точек другой таблицей близких к
ним точек, лежащих на достаточно гладкой кривой.
Сглаживание производится с помощью многочленов (желательно
оптимальной степени), приближающих по методу наименьших
квадратов выбранные группы опытных точек. Так как наилучшее
сглаживание получается для средних точек (когда учитывается
информация о поведении функции по обе стороны от сглаживаемой
точки), то количество точек для сглаживания выбирают нечетным, а
группы точек–скользящими вдоль всей таблицы: берут, например,
первые пять точек y1 , y2 , y3 , y4 , y5 и сглаживают с их помощью
среднюю точку y3 , затем берут следующую группу точек
y2 , y3 , y4 , y5 , y6 и сглаживают точку y 4 , и т.д. до конца таблицы. При
этом остаются несколько крайних точек, которые сглаживаются с
меньшей точностью.
Ниже приводятся наиболее употребляемые из простых формул
сглаживания для таблиц с постоянным шагом. Сглаженные значения
обозначаются волнистой чертой сверху. Основной формулой служит
~
формула сглаживания средней точки, т.е. формула для f i , остальные
формулы применяются только на краях таблицы.
Наиболее простым методом является метод линейного
сглаживания по трем точкам: Линейным сглаживанием называется
сглаживание многочленом первой степени.
~
f i = [ f i −1 + f i + f i +1 ] / 3, i = 1,2,...n − 1 ,
~
f 0 = [5 f 0 + 2 f i − f 2 ] / 6, i = 0 ,
~
f n = [5 f n + 2 f n −1 − f n − 2 ] / 6, i = n ,
где n -номер последней точки, в которой измерена величина f i .
Метод линейного сглаживания по пяти точкам основан на
использовании формул
~
f 0 = [3 f 0 + 2 f i + f 2 − f 4 ] / 5, i = 0 ,
~
f1 = [4 f 0 + 3 f i + 2 f 2 + f 3 ] / 10, i = 1 ,
~
f i = [ f i − 2 + f i −1 + f i + f i +1 + f i + 2 ] / 5, i = 2,3,...n − 2
~
f n −1 = [4 f n + 3 f n −1 + 2 f n − 2 + f n − 3 ] / 10, i = n − 1
~
f n = [3 f n + 2 f n −1 + f n − 2 − f n − 4 ] / 5, i = n
Метод нелинейного сглаживания по семи точкам обеспечивает
усреднение на основе применения полинома третьей степени и
реализуется следующими формулами:
~
f 0 = [39 f 0 + 8 f1 − 4( f 2 + f 3 − f 4 ) + f 5 − 2 f 6 ] / 42 ,
~
f1 = [8 f 0 + 19 f1 + 16 f 2 + 6 f 3 − 4 f 4 − 7 f 5 + 4 f 6 ] / 42 ,
~
f 2 = [− 4 f 0 + 16 f1 + 19 f 2 + 12 f 3 + 2 f 4 − 4 f 5 + f 6 ] / 42 ,
~
f i = [7 f i + 6( f i +1 + f i −1 ) + 3( f i + 2 + f i − 2 ) − 2( f i + 3 + f i − 3 )] / 21 ,
~
f n − 2 = [− 4 f n + 16 f n −1 + 19 f n − 2 + 12 f n − 3 + 2 f n − 4 − 4 f n − 5 + f n − 6 ] / 42
~
f n −1 = [8 f n + 19 f n −1 + 16 f n − 2 + 6 f n − 3 − 4 f n − 4 − 7 f n − 5 + 4 f n − 6 ] / 42 ,
~
f n = [39 f n + 8 f n −1 − 4( f n − 2 + f n − 3 − f n − 4 ) + f n − 5 − 2 f n − 6 ] / 42
Формулы сглаживания многочленами более высоких степеней не
применяются, а формулы сглаживания по большему числу точек
применяются крайне редко, так как они оставляют плохо сглаженными
большое количество точек по краям таблицы.