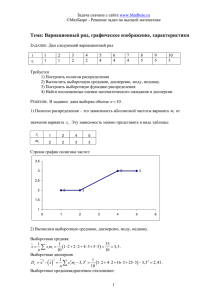
X генеральная дисперсия: ,

М.В.Дубатовская. Теория вероятностей и математическая статистика
Лекция 15
§ 7. Дисперсия
Рассеяние значений признака X генеральной совокупности вокруг среднего значения характеризует генеральная дисперсия:
N
xГ )2
( xi
i 1
DГ
,
N
xi , i 1, n , - все значения признака генеральной совокупности объема N .
Если значения признака x1 , x2 ,..., xk имеют частоты N1 , N 2 ,..., N k , причем
N1 N 2 ... N k N , то
k
Ni ( xi
DГ
xГ ) 2
i 1
.
N
Генеральным средним квадратическим отклонением (с.к.о.) называется величина:
DГ
Г
Для характеристики рассеяния значений количественного признака выборки вокруг
своего среднего значения x вводят выборочную дисперсию:
n
xВ ) 2
( xi
DВ
n1
Если значения
n2 ... nk n , то
признака
i 1
n
x1 , x2 ,..., xk
имеют
частоты
n1 , n2 ,..., nk ,
причем
k
ni ( xi
DВ
Выборочное с.к.о.
В
i 1
n
xВ ) 2
.
DВ .
Дисперсию можно также вычислять по формуле: D x 2 (x )2 .
Допустим. что все значения количественного признака X совокупности (генеральной или выборочной) разбиты на k групп. Рассматривая каждую группу как самостоятельную совокупность, можно найти групповую среднюю и дисперсию значений признака, принадлежащих группе, относительно групповой средней.
Групповой дисперсией называют дисперсию значений признака, принадлежащих
группе, относительно групповой средней:
М.В.Дубатовская. Теория вероятностей и математическая статистика
x j )2
ni ( xi
i
Dгр. j
,
Nj
ni - частота значения xi ,
j - номер группы,
Nj
ni - объем группы.
i
Внутригрупповой дисперсией называют среднюю арифметическую групповых
дисперсий, взвешенную по объемам групп:
N j Dгр. j
j
Dвн .гр.
N j - объем группы, n
k
,
n
N j - объем совокупности.
j 1
Зная групповые средние и общую среднюю, можно найти дисперсию групповых
средних относительно общей средней.
Межгрупповой дисперсией называют дисперсию групповых средних относительно общей средней:
N j (x j
Dмежгр
j
n
x )2
,
где x j - групповая средняя j -той группы,
N j - объем j -той группы,
x - общая средняя,
n - объем всей совокупности.
Замечание. Dобщ Dвнгр
D межгр .
§ 8. Оценка генеральной дисперсии по исправленной выборочной дисперсии
Пусть из генеральной совокупности извлечена выборка объема n . Значения признака x1 , x2 ,..., xk имеют частоты n1 , n2 ,..., nk , причем n1 n2 ... nk n .
Требуется по данным выборки оценить неизвестную генеральную дисперсию DГ .
Если в качестве такой оценки принять выборочную дисперсию, то эта оценка будет
приводить к систематическим ошибкам, давая заниженной значение генеральной дисперсии. Это объясняется тем, что DВ является смещенной оценкой DГ , т.к.
n 1
M ( DB )
DГ .
n
Выборочную дисперсию можно «исправить» так, что математическое ожидание
стало равным DГ .
Рассматривают исправленную дисперсию
М.В.Дубатовская. Теория вероятностей и математическая статистика
k
s2
n
n 1
DВ
k
ni ( xi
n
xВ ) 2
i 1
n 1
ni ( xi
xВ ) 2
i 1
n
n 1
.
Исправленная дисперсия является несмещенной оценкой генеральной дисперсии:
M (s 2 )
M(
n
n 1
DВ )
n
n 1
DГ
n 1 n
DГ .
Для оценки с.к.о. генеральной совокупности также используется исправленное с.к.о.:
s
s 2 . Заметим, что s не является несмещенной оценкой.