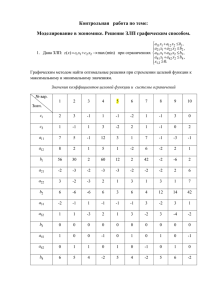
инструкции и таблицы

Числа в первой строке обозначить x1 , x2 , . . . , x10 , Во второй строке
обозначить y1 , y2 , . . . , y10 ,
На самом деле все двадцать чисел моделируются как нормальные числа с одними и теми же параметрами
Задания.
1) Вычислить эмпирические средние и дисперсию x–ов и y–ов,
2) Указать для среднего и дисперсии несмещенные оценки.
3) Построить график эмпирической функции распределения для x–ов.
4) Построить доверительные интервалы для среднего (симметричный)
и дисперсии (вида (0, ε)) x–ов и y–ов с доверительным уровнем 0.9.
5) Вычислить коэффициент корреляции между x–ми и y–ми с одинаковыми номерами (мы рассматриваем векторные данные (x1 , y1 ), . . . , (x10 , y10 )
Проверить гипотезу независимости x-ов и y-ов с уровнем значимости 0.1
и 0.096.
6) С помощью критерия Стьюдента проверить с уровнем значимости
0.1 гипотезу равенства средних x–ов и y–ов при альтернативной гипотезе
“среднее x–ов больше среднего y-ов”.
7) Создать единую выборку из 20 данных, переписав подряд сначала
все xi , потом все yi , подсчитать коэффициент d и коэффициент асимметрии g и проверить на нормальность двумя способами с уровнями
значимости 0.1 и 0.02).
8) Подсчитать ранговый коэффициент корреляции Спирмена, сравнить с обычным коэффициентом корреляции. Проверить с помощью рангового коэффициента гипотезу независимости x-ов и y-ов с уровнем значимости 0.096.
Объяснить все, что делается, своими словами.
Все приведенные ниже таблицы взяты из таблиц Большева и Смирнова в предположении нормальности выборки из 20 данных.
Таблица P{d ≥ d0 } = p0 , где числа d0 , для которых соответствующая
вероятность равна p0 указаны в таблице, а вероятности указаны сверху,
сбоку указаны числа n = 16, 21, а у вас n = 20, значит нужна интерполяция.
P Уровень значимости критерия вы сделайте равным 0.02 и 0.10.
|x −x̄|
d = i n·si , где s2 — эмпирическая дисперсия.
P
(x −x̄)3
Таблица для выборочного коэффициента асимметрии g = i n·si 3 .
В таблице для соответствующего значения вероятности p0 и числа наблюдений n указаны g0 , для которых P{g ≥ g0 } = p0 . Используя симмет1
ричность распределения асимметрии, можно построить критерии с уровнями значимости 0.1 и 0.02 для n = 25, 30, 35. К сожалению, в таблице
нет значений g0 для n = 20, поэтому нужно провести экстраполяцию
(лучше говорить экстраполяция, а не интерполяция, так как 20 выходит
за рамки данных таблицы) с помощью полинома второго порядка.
Подробнее все это написано ниже в соответствующей таблице.
2
ТАБЛИЦЫ ВЕРОЯТНОСТЕЙ [1]
1. Л.Н. Большев, Н.В. Смирнов. Таблицы математической статистики.
М. Наука, 1983.
Таблица 1. Функция распределения Φ
стандартного нормального распределения:
Zx
Φ(x) =
−∞
x2
1
√ e− 2 dx.
2π
Горизонтальная часть таблицы указывает сотые доли x. Значения Φ
умножены на 104 .
x
0.0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1.0
1.1
1.2
1.3
1.4
1.5
1.6
1.7
1.8
1.9
2.0
0
5000
5398
5793
6179
6554
6915
7257
7580
7881
8159
8413
864
8849
9032
9192
9332
9452
9554
9641
9713
9772
1
5040
5438
5832
6217
6591
6950
7291
7611
7910
8186
8437
8665
8869
9049
9207
9345
9463
9564
9649
9719
9778
2
5080
5478
5871
6256
6628
6985
7324
7642
7939
8212
8461
8686
8888
9066
9222
9357
9474
9573
9656
9726
9783
3
5120
5517
5910
693
6664
7019
7357
7673
7967
8238
8485
8708
8907
9082
9236
9370
9484
9582
9664
9732
9788
4
5160
5557
5948
6331
6700
7054
7389
7703
7995
8264
8508
8729
8925
9099
9251
9382
9495
8591
9671
9738
9793
3
5
5200
5596
5987
6338
6736
7088
7422
7734
8023
8289
8381
8749
8944
9115
9255
9394
9505
9599
9678
9744
9798
6
5239
5636
6026
6406
6772
7123
7454
7764
8051
8315
8554
8770
8962
9131
9279
9406
9515
9608
9686
9750
9803
7
5279
5675
6064
6443
6808
7157
7486
7794
8078
8340
8577
8790
8980
9147
9292
9418
9525
9616
9693
9756
9808
8
5319
5714
6103
6480
6844
7190
7517
7823
8106
8365
8599
8810
8997
9162
9306
9429
9535
9625
9699
9761
9812
9
5359
5753
6141
6517
6879
7224
7549
7852
8133
8389
8621
8831
9015
9177
9319
9441
9545
9633
9705
9767
9817
x
2.1
2.2
2.3
2.4
2.5
2.6
2.7
2.8
2.9
3.0
0
9821
9861
9893
9918
9938
9953
9965
9974
9981
9987
1
9825
9864
9896
9920
9940
9955
9966
9975
9982
9987
2
9830
9868
9898
9922
9941
9956
9967
9976
9982
9987
3
9834
9871
9901
9925
9943
9957
9968
9977
9983
9988
4
9838
9875
9904
9927
9945
9959
9969
9977
9984
9988
5
9842
9878
9906
9929
9946
9960
9970
9978
9984
9989
6
9846
9881
9909
9931
9948
9961
9971
9979
9985
9989
7
9850
9884
9911
9932
9949
9962
9972
9979
9985
9989
8
9854
9887
9913
9934
9951
9963
9973
9980
9986
9990
9
9857
9890
9915
9936
9952
9964
9974
9981
9986
9990
Таблица 2. (1 − p)-квантиль q распределения χ2 :
2
P{χn > q} = p.
n\p 0.99
0.975 0.95
0.9
2 0.0201 0.0506 0.103 0.211
3 0.115 0.216 0.352 0.584
4 0.297 0.484 0.711 1.064
5 0.554 0.831 1.145 1.610
6 0.872 1.237 1.635 2.204
7 1.239 1.690 2.167 2.833
8 1.646 2.180 2.733 3.490
9 2.088 2.700 3.325 4.168
10 2.558 3.247 3.940 4.865
11 3.053 3.816 4.575 5.578
12 3.571 4.404 5.226 6.304
13 4.107 5.009 5.892 7.042
14 4.660 5.629 6.571 7.790
15 5.229 6.262 7.261 8.547
16 5.812 6.908 7.962 9.312
17 6.408 7.564 8.672 10.085
18 7.015 8.231 9.390 10.865
19 7.633 8.907 10.117 11.651
20 8.260 9.591 10.851 12.443
4
0.1
4.605
6.251
7.779
9.236
10.645
12.017
13.362
14.684
15.987
17.275
18.549
19.812
21.064
22.307
23.542
24.769
25.989
27.204
28.412
0.05
5.991
7.815
9.488
11.070
12.592
14.067
15.507
16.919
18.307
19.675
21.026
22.362
23.685
24.996
26.296
27.587
28.869
30.144
31.410
0.025
7.378
9.348
11.143
12.832
14.449
16.013
17.535
19.023
20.483
21.920
23.336
24.736
26.119
27.488
28.845
30.191
31.526
32.852
34.170
0.01
9.210
11.345
13.277
15.086
16.812
18.475
20.090
21.666
23.209
24.725
26.217
27.688
29.141
30.578
32.000
33.409
34.805
36.191
37.566
n\p
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
0.99
8.897
9.542
10.196
10.856
11.524
12.198
12.879
13.565
14.256
14.953
15.655
16.362
17.073
17.789
18.509
19.233
19.960
20.691
21.426
22.164
0.975
10.283
10.982
11.688
12.401
13.120
13.844
14.573
15.308
16.047
16.791
17.539
18.291
19.047
19.806
20.569
21.336
22.106
22.878
23.654
24.433
0.95
11.591
12.338
13.091
13.848
14.611
15.379
16.151
16.928
17.708
18.493
19.281
20.072
20.867
21.664
22.465
23.269
24.075
24.884
25.695
26.509
0.9
13.240
14.041
14.848
15.659
16.473
17.292
18.114
18.939
19.768
20.599
21.434
22.271
23.110
23.952
24.797
25.643
26.492
27.343
28.196
29.051
0.1
29.615
30.813
32.007
33.196
34.382
35.563
36.741
37.916
39.087
40.256
41.422
42.585
43.745
44.903
46.059
47.212
48.363
49.513
50.660
51.805
0.05
32.671
33.924
35.172
36.415
37.652
38.885
40.113
41.337
42.557
43.773
44.985
46.194
47.400
48.602
49.802
50.998
52.192
53.384
54, 572
55.758
0.025
35.479
36.781
38.076
39.364
40.646
41.923
43.194
44.461
45.722
46.979
48.232
49.480
50.725
51.966
53.203
54.437
55.668
56.895
58.120
59.342
0.01
38.932
40.289
41.638
42.980
44.314
45.642
46.963
48.278
49.588
50.892
52.191
53.486
54.776
56.061
57.342
58.619
59.892
61.162
62.428
63.691
Таблица 3. (1 − p)-квантиль q распределения Стьюдента
случайной величины tn : P{tn > q} = p.
5
n\p
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
n\p
28
29
30
32
34
36
38
40
42
44
46
48
50
55
60
65
70
80
90
100
120
150
200
250
300
400
500
0.05
0.025
0.01 6.3138 12.7062 31.8205 2.9200 4.3027 6.9646 3534 3.1824 4.5407 1318 2.7764 3.7469 0150
5706
3649 1.9432 2.4469 3.1427 8946
3646 2.9980 8595
3060
8965 8331
2622
8214 8125
2281
7638 1.7959 2.2010 2.7181 7823
1788
6810 7709
1604
6503 7613
1448
6245 7530
1314
6025 1.7459 2.1199 2.5835 7396
1098
5669 7341
1009
5524 7291
0930
5395 7247
0860
5280 1.7207 2.0796 2.5176 7171
0739
5083 7139
0687
4999 7109
0639
4922 7081
0595
4851 7056
0555
4786 1.7033 2.0518 2.4727 6
0.05
1.7011
6991
6973
6939
6909
6883
6860
6839
1.6820
6802
6787
6772
6759
2.6730
6706
6686
6669
6641
6620
1.6602
6577
6551
6525
1.6510
6499
6487
1.6479
0.025
2.0484
0452
0423
0369
0322
0281
0244
0211
2.0181
0154
0129
0106
0086
2.0040
0003
1.9971
9944
9901
9867
1.9840
9799
9759
9719
1.9695
9679
9659
1.9647
0.01
2.4671
4620
4573
4487
4411
4345
4286
4233
2.4185
4141
4102
4066
4033
2.3961
3901
3851
3808
3739
3685
2.3642
3578
3515
3451
2.3414
3388
3357
2.3338
Таблица 4. 0.95-квантиль q распределения Фишера
случайной величины
Fm,n =
n\m
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
161.5
18.51
10.13
7.709
6.608
5.987
5.591
5.318
5.117
4.965
4.844
4.747
4.667
4.600
4.543
4.494
2
199.5
19.00
9.552
6.944
5.786
5.143
4.737
4.459
4.257
4.103
3.982
3.885
3.806
3.739
3.682
3.634
3
215.7
19.16
9.277
6.591
5.410
4.757
4.347
4.066
3.866
3.709
3.587
3.490
3.411
3.344
3.287
3.239
nχ2m
, P{Fm.n > q} = 0.05.
mχ2n
4
224.6
19.25
9.117
6.388
5.192
4.534
4.120
3.838
3.633
3.478
3.357
3.259
3.179
3.112
3.056
3.007
5
230.2
19.30
9.014
6.256
5.050
4.387
4.972
3.688
3.482
3.326
3.204
3.106
3.025
2.958
2.901
2.852
6
234.0
19.33
8.941
6.163
4.950
4.284
3.866
3.581
3.374
3.217
3.095
2.996
2.915
2.848
2.791
2.741
7
236.8
19.35
8.887
6.094
4.876
4.207
3.787
3.501
3.293
3.136
3.012
2.913
2.832
2.764
2.707
2.657
8
238.9
19.37
8.845
6.041
4.818
4.147
3.726
3.438
3.230
3.072
2.948
2.849
2.767
2.699
2.641
2.591
9
240.5
19.39
8.812
5.999
4.773
4.099
3.677
3.388
3.179
3.020
2.896
2.796
2.714
2.646
2.588
2.538
10
241.9
19.40
8.786
5.964
4.735
4.060
3.637
3.347
3.137
2.978
2.854
2.753
2.671
2.602
2.544
2.494
Таблицы, используемые при проверке выборки
на нормальность
В следующих таблицах для выборки (x1 , ..., xn ) используются стандартные обозначения:
n
x1 + ... + xn
1X
2
x̄ =
, s =
(xi − x̄)2 .
n
n i=1
Таблица 5. (1 − p)-квантиль q распределения
выборочной характеристики эксцесса
в нормальной модели с выборкой (x1 , ..., xn )
7
n
1X
(xi − x̄)4
n i=1
Эксцесс обозначается в [30] b2 − 3 =
− 3.
s4
Число в таблице q определяется равенством P {b2 − 3 > q} = p.
n\p
50
100
150
200
250
0.01
1.92
1.40
1.14
0.98
0.87
0.05
1.01
0.77
0.66
0.57
0.51
0.95
−0.87
−0.65
−0.55
−0.49
−0.45
0.99
−1.05
−0.82
−0.70
−0.63
−0.58
Таблица 6. (1 − p)-квантиль q распределения
выборочной характеристики асимметрии g1
в нормальной модели с выборкой (x1 , ..., xn )
n
1X
(xi − x̄)3
n
Асимметрия обозначается в [30] g1 = i=1 3
.
s
Число в таблице q определяется равенством P {g1 > q} = p.
n \ p 0.05 0.01 √Dg1 25 0.711 1.061 0.4354 30 0.661 0.982 0.4052 35 0.621 0.921 0.3804 40 0.587 0.869 0.3596 45 0.558 0.825 0.3418 50 0.533 9, 787 0.3264 60 9.492 0.723 0.3009 70 0.459 0.673 0.2806 80 0.432 0.631 0.2638 90 0.409 0.596 0.2498 100 0.389 0.567 0.2377 Таблица 7. (1 − p)-квантиль q распределения
выборочной характеристики d в нормальной модели
8
1
n
n
X
с выборкой (x1 , ..., xn )
|xi − x̄|
.
d = i=1 s
Число в таблице q определяется равенством P {d > q} = p.
√ n\p
0.01
0.05
0.1
0.9
0.95
0.99
Dd 11 0.9359 0.9073 0.8899 0.7409 0.7153 0.6675 0.05784 16 9137 8884 8733 7452 7236 6829 0.04976 21 9001 8768 8631 7495 7304 6950 0.04419 26 8901 8686 8570 7530 7360 7040 0.04011 31 8827 8625 8511 7559 7404 7110 0.03697 36 8769 8578 8468 7583 7440 7167 0.03447 41 8722 8540 8436 7604 7470 7216 0.03241 46 8682 8508 8409 7621 7496 7256 0.03068 51 8648 8481 8385 7636 7518 7291 0.02919 61 0.8592 0.8434 0.8349 0.7662 0.7554 0.7347 0.02678 71 8549 8403 8321 7683 7583 7393 0.02487 81 8515 8376 8298 7700 7607 7430 0.02332 91 8484 8353 8279 7714 7626 7460 0.02203 101 8460 8344 8264 7726 7644 7487 0.02094 Примечание. Для таблиц 6 и 7 для n, отличных от использованных в
таблице, в [1] предлагается использовать линейную интерполяцию или
экстраполяцию. Причем интерполяция или экстраполяция должны про√
водиться
не
по
аргументу
n,
а
по
аргументу
Dg1 в таблице 6 и по аргу√
менту Dd в таблице 7. Там же приведены формулы для дисперсий:
6(n − 2)
(n + 1)(n + 3)
"
#2
n−1
p
1
2
1
n−1 Γ 2
Dd =
1+
n(n − 2) + arcsin
−
.
n
π
n−1
π
Γ n2
Dg1
=
Таблица 8. Функция распределения рангового коэффициента
корреляции Спирмена ρ
9
В таблице для каждого числа наблюдений n указаны вероятности
p(n) = P{ρ ≤ r(n)}, где числа r(n) пробегают значения (не все), которые
для данного n может принимать ρ.
r(6)
p(6)
90
− 210 0.210
102
− 210
0.178
114
− 210 0.149
126
− 210
0.121
138
− 210 0.088
150
− 210
0.068
162
− 210 0.051
174
− 210
0.029
186
− 210
0.017
198
− 210 0.0083
r(7)
p(7) r(8)
p(8) r(9)
p(9) r(10) p(10) 216
− 116
0.249 − 144
0.250 − 720
0.218 − 258
0.235 336
504
990
264
− 128
0.198 − 180
0.195 − 720
0.168 − 318
0.184 336
504
990
312
− 140
0.151 − 216
0.150 − 720
0.125 − 378
0.139 336
504
990
360
− 152
0.118 − 252
0.108 − 720
0.089 − 438
0.102 336
504
990
408
− 164
0.083 − 288
0.076 − 720
0.060 − 498
0.072 336
504
990
456
− 176
0.055 − 324
0.048 − 720
0.038 − 558
0.048 336
504
990
360
504
618
− 188
0.033
−
0.029
−
0.022
−
0.030
336
504
720
990
396
552
678
− 200
0.017
−
0.014
−
0.011
−
0.017
336
504
720
990
432
600
738
− 212
0.0062
−
0.0054
−
0.0041
−
0.0087
336
504
720
990
224
468
648
798
− 336 0.0014 − 504 0.0011 − 720 0.0010 − 990 0.0036 10