LuminEcool
реклама

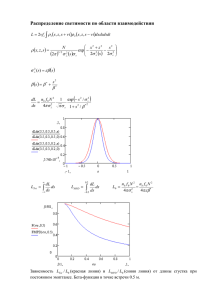
Светимость коллайдера NICA, роль охлаждения А.Сидорин, А.Смирнов Черновик, 4 апреля 2007 г. Аннотация Показано, что в коллайдере NICA светимость ограничена не эффектом встречи, а Ласслетовским сдвигом бетатронного числа. Для получения пиковой светимости NICA равной 1027 см2с-1 на энергии 2.5 ГэВ/н необходимо 21010 ионов в каждом кольце, а при энергии 3.5 ГэВ/н ~ 1010. Максимальную пиковую светимость можно достичь и без применения охлаждения на энергии эксперимента, за счет увеличения смещения бетатронного числа при финальной группировке. Максимально допустимый номер гармоники ВЧ определяется требованием исключить паразитные точки встречи в районе детектора, и равен примерно 20. Основным эффектом, ограничивающим время жизни светимости (в отсутствии охлаждения на энергии эксперимента) является внутрипучковое рассеяние. При этом снижение светимости со временем существенно более медленное, чем экспоненциальное. Приведены параметры пучка, позволяющие рассчитать характерные времена ВПР, и оценить возможность достижения требуемой средней светимости без применения охлаждения на энергии эксперимента. Схема с охлаждением на энергии эксперимента пока не рассматривалась. 0. Введение 0.1. Рабочая схема комплекса, роль охлаждения в проекте В качестве рабочей схемы комплекса представляется привлекательным принять за основу структуру и основные параметры, предложенные в [В.А.Михайлов, Теплый бустер, материалы проекта NICA] Таблица на следующей странице. Основные приводимые здесь выводы не зависят от конкретных особенностей схемы, таких как: энергия инжекции в Нуклотрон, схема накопления в бустере и Нуклотроне, тип инжекции в коллайдер, режим работы коллайдера (с ускорением или без ускорения). Наиболее существенный вывод из предложенной схемы (а он подтверждает и предыдущие оценки, и мнение экспертов по проекту): без активных методов формирования эмиттанса пучка и разброса по импульсу рассчитывать на получение проектной светимости не приходится. Так, кинематическое затухание эмиттанса от энергии инжекции в бустер до энергии эксперимента приводит к конечному его значению порядка нескольких мммрад, тогда как для получения светимости требуется почти на порядок меньше. Ситуация с эмиттансом только ухудшится, если проектировать бустер на большую энергию и больший аксептанс. В приведенной схеме аксептанс бустера выбран таким образом, чтобы при его полном заполнении после ускорения до энергии инжекции в Нуклотрон эмиттанс пучка был несколько меньше аксептанса Нуклотрона. И при выбранной конечной энергии увеличение аксептанса бустера не имеет смысла. Формирование фазового объема пучка необходимо осуществлять в коллайдере, иначе невозможно будет скомпенсировать возможные искажения при инжекции и эффективно провести накопление в коллайдере. Несмотря на то, что в таблице приведен вариант коллайдера с ускорением, но данная схема не исключает и режим работы без ускорения, если промежуточная обдирка пучка осуществляется после Линака. Режим без ускорения в коллайдере весьма привлекателен в случае необходимости осуществить столкновения ионов разного сорта. Дополнительным аргументом в пользу данной схемы может служить возможность размещения стрипперов для конечной обдирки непосредственно в кольцах коллайдера и использовать схему накопления с однооборотной перезарядной инжекцией, хорошо зарекомендовавшую себя в ИТЭФ. Причем, если копить на 1 ГэВ/н, то все параметры достаточно близки к ИТЭФ-овским, и необходимые исследования можно пробовать организовать на их базе. Они собираются копить тяжелые ионы с энергией 700 кэВ/н до интенсивности 1013 частиц. В свое время в СЭО ЛЯП был разработан проект системы электронного охлаждения для накопителя ТВН ИТЭФ, и основные технические решения для энергии электронов до 350 кэВ были выработаны. NICA LAYOUT Stripper EBIS LINAC BOOSTER NUCLOTRON COLLIDER Ions Energy MeV/Amu Injection U30+ U30+ 5 U30+ 50 U30+ 1000 U92+ 2500 2 turn stacking 1 turn Intensity 1 0.5 3 turn stacking 1.5 3 3 Emittance πmm mrad 1 10 100 → 30 30 → 6 6→3 0.1. Коллайдер с ускорением При работе коллайдера в режиме с ускорением, и охлаждением только на энергии инжекции, время жизни светимости определяется только внутрипучковым рассеянием: потери частиц пренебрежимо малы (время жизни пучка – несколько суток). При этом работу коллайдера можно организовать в такой временной последовательности: - накопление требуемого числа частиц; - формирование требуемого эмиттанса и разброса по импульсу; – ускорение при невысоком факторе группировки; – адиабатическая догруппировка (повышение амплитуды ВЧ); – эксперимент; – понижение фактора группировки (понижение амплитуды ВЧ); – торможение; – инжекция небольшого количества частиц для компенсации потерь при рекомбинации в секции охлаждения; – формирование фазового объема пучка; – и т.д. по циклу. При этом, в течение основного цикла работы, потери частиц имеют место только при «подохлаждении» пучка, и к темпу рекомбинации в секции охлаждения не такие жесткие требования: например, за время охлаждения потерять не более n% частиц. Время первоначального накопления пучка в задачу о средней светимости не входит, так как оно осуществляется один раз при «загрузке». Фактор заполнения определяется временем торможения и ускорения в коллайдере, и временем «подохлаждения». 0.2. Ожидаемая интенсивность При существующих параметрах источника KRION – интенсивность 5108 ионов за импульс (при частоте повторения 40 Гц – при предложенной схеме с тремя импульсами в бустер, частота повторения практически в задачу не входит) по предложенной схеме для одной загрузки Нуклотрона требуется 2 цикла бустера, по 2 сек каждый. В результате имеем 1.5109 ионов. Если цикл Нуклотрона положить равным 6 сек (от фонаря), то мы будем иметь темп поступления ионов на вход коллайдера не меньше чем примерно 1.5 10 9 ~ 1.5108 с-1. Полное число ионов, которое можно накопить составляет N 622 N max N life , где life – время жизни ионов в кольце коллайдера. Насыщение интенсивности достигается при времени накопления порядка (2 – 3)life. Если основной механизм потерь ионов связан с рекомбинацией в секции электронного охлаждения, то без специальных мер по ее подавлению характерное время жизни будет порядка 100 сек. Соответственно, по ИТЭФ схеме можно накопить до 1.51010 ионов за 300 сек х 2 (оба кольца) = 10 минут. Подавив рекомбинацию, можно или увеличить предельное число ионов, или, при той же конечной интенсивности, сократить время накопления. Таким образом, уже при существующей интенсивности источника, при грамотном проектировании системы охлаждения, можно смело обсуждать проведение эксперимента с 1010 – 1011 ионов в каждом кольце. 0.3. Коллайдер без ускорения В режиме работы коллайдера без ускорения, рабочий диапазон энергии системы охлаждения должен перекрывать весь диапазон энергий, интересных для эксперимента. Нет никаких сомнений в том, что такая система может быть сконструирована и изготовлена в ОИЯИ, но будет, возможно, существенно дороже. В этом случае эксперимент сопровождается потерями частиц в результате рекомбинации в секции охлаждения. Соответственно, рекомбинацию нужно подавить на один два порядка. Технология этого хорошо освоена, но требует перехода от полей в секции охлаждения в 12 кГс, типичных для обычных систем, к полям 2 – 3 Тл. При использовании сверхпроводящих соленоидов это не представляет проблемы. При достаточно большом количестве ионов, при охлаждении в процессе эксперимента можно организовать режим с примерно постоянной светимостью (за счет постепенного увеличения темпа охлаждения (тока электронного пучка) и компенсации потерь путем уменьшения эмиттанса). Но при этом с некоторой периодичностью нужно восполнять потери частиц. Скорее всего, для этого потребуются некоторые манипуляции с ионным пучком (например: распустить – добавить – сгруппировать). Но в целом режим работы инжекционного комплекса аналогичен предыдущему параграфу. 0.4. Вопросы Если планировать работу коллайдера с ускорением в нем ионов, то нужно ли охлаждение и на энергии эксперимента? А какая, собственно, интенсивность и яркость пучка нам нужны? 1. Ограничения пиковой светимости 1.1. Основные эффекты, ограничивающие светимость Для двух одинаковых сталкивающихся сгустков круглого сечения светимость может быть оценена следующей формулой: L N2 1 , h 4*Trev (1.1) где N – полное число частиц в каждом из колец коллайдера, h – номер гармоники ВЧ поля (предполагается, что все сепаратриссы заполнены одинаковыми сгустками), поперечный среднеквадратичный эмиттанс пучка, * - бетатронная функция в точке встречи, Trev – период обращения ионов в накопителе. Из формулы (1.1) понятно, что при ограниченном числе частиц, максимальная пиковая светимость достигается при минимальном значении эмиттанса, который, в свою очередь, ограничен снизу развитием неустойчивости. Смысл применения охлаждения – при некотором заданном числе частиц уменьшить эмиттанс до минимально достижимой величины и, тем самым, получить максимальную светимость. При большом запасе по числу частиц можно работать и вдали от неустойчивости, но, предвидя некоторые трудности в получении интенсивного пучка, а так же из соображений радиационной безопасности и т.п., оценим минимально необходимое число частиц и будем ориентироваться на уменьшение эмиттанса за счет охлаждения В зависимости от параметров накопителя может достигаться либо порог по кулоновскому сдвигу бетатронных чисел, либо порог по эффекту встречи. Когерентные неустойчивости пучка можно избежать за счет аккуратного конструирования вакуумной камеры (чтобы уложиться в требования по импедансам), соответствующего выбора хроматичностей и разброса по импульсу (чтобы увеличить разброс частот колебаний) или подавить за счет применения системы обратной связи. Эффект встречи характеризуется линейной частью сдвига бетатронных чисел из-за взаимодействия со встречным сгустком – так называемым «параметром столкновений» или «бим-бим» параметром. Пороговое значение сдвига частоты колебаний по параметру встречи для ионных коллайдеров соответствует примерно 0.005. Максимальный кулоновский сдвиг бетатронного числа может достигать 0.05. При интенсивном охлаждении можно надеяться повысить сдвиг бетатронного числа до 0.2 (максимальное значение, полученное при электронном охлаждении), а «бим-бим» параметр примерно на порядок. Для круглого пучка «бим-бим» параметр равен Z 2 rp 1 N 1 2 . A h 4 2 (1.2) Кулоновский сдвиг может быть приблизительно оценен по формуле Q Z 2 rp N A 4 2 3 Fsc Fb , (1.3) где Fsc – фактор коррекции сил изображения (обычно порядка 1 и в дальнейшем мы его опустим). C/h (1.4) Fb 2 s - оценка отношения пикового тока к среднему или фактор группировки (отношение длины сепаратриссы C/h к полной длине сгустка, s – среднеквадратичная длина сгустка). Соотношение между кулоновским сдвигом бетатронных чисел и «бим-бим» параметром определяется энергией пучка и фактором группировки Q 2 1 2 1 2 C . 2 s (1.5) Для того, чтобы избежать снижения светимости из-за эффекта «песочных часов» длина сгустка должна удовлетворять условию s (0.6 1)*. Таким образом, при выбранном значении бетатронной функции в точке встречи, эффект, которым ограничивается светимость определяется только периметром кольца и энергией частиц. Например, при параметрах RHIC, когда Лоренц фактор примерно равен 100, сдвиг бетатронного числа в несколько раз меньше «бим-бим» параметра, и именно эффект встречи ограничивает достижимую величину светимости. Сейчас они имеют 0.0015, а Q 0.0005. Применением охлаждения они рассчитывают поднять «бим-бим» параметр до порога неустойчивости и на этом выиграть в светимости. С уменьшением энергии ситуация изменяется и при нескольких ГэВ/н основным ограничением становится сдвиг бетатронного числа. При текущих параметрах коллайдера NICA мы ограничены именно этим эффектом. Но на энергии 3.5 ГэВ/н оба порога достаточно близки. (Если, вдруг, пойдем на большую энергию, то, возможно, наткнемся и на эффект встречи.) Если светимость ограничена эффектом встречи, то она может быть выражена через параметр столкновений как L A N 2 , 2 * Z rp Trev 1 2 (1.6) В оценках периметр коллайдера примем равным 194 м, а бетатронную функцию в точке встречи 0.5 м, и все оценки проведем для ядер урана. Тогда, при энергии пучка 2.5 Гэв/н L cm 2 s 1 2 1019 N , а при энергии 3.5 ГэВ/н L cm 2 s 1 2.6 1019 N . Если светимость ограничена кулоновским сдвигом бетатронного числа Q, то она может быть выражена как: L A N 2 * Z rp Trev 2 s 3 2 Q . C (1.7) Предполагая, что s = 0.6*, при энергии 2.5 Гэв/н это дает L cm 2 s 1 9.7 1017 N Q , а при энергии 3.5 ГэВ/н L cm 2 s 1 2.2 1018 N Q . Из этих оценок видно, что даже, несмотря на то, что кулоновский сдвиг может быть примерно на порядок больше «бим-бим» параметра, светимость при обеих энергиях NICA ограничена именно кулоновским сдвигом. И, например, при Q = 0.05, для получения светимости 1027 см2с-1 на энергии 2.5 ГэВ/н необходимо 21010 ионов в каждом кольце, а при энергии 3.5 ГэВ/н ~ 1010. 1.2. Выбор бета-функции в точке встречи, сравнение по светимости с RHIC По поводу формулы (1.7) стоит сделать такое замечание. Несмотря на то, что бетатронная функция в точки встречи, вроде бы, в явном виде присутствует в этой формуле, максимальная светимость от нее зависит очень слабо. Это объясняется тем, что при уменьшении бетатронной функции, чтобы избежать потери светимости из-за эффекта «песочных часов», необходимо пропорционально уменьшать и длину сгустка. При этом то же значение сдвига бетатронного числа достигается при большем значении эмиттанса, и, в результате, светимость остается неизменной. (Более точную оценку можно сделать, введя в формулу (1.7) зависимость светимости от отношения длины сгустка к бетатронной функции в точке встречи.) Такая ситуация принципиально отличается от случая, когда светимость ограничена эффектом встречи. При ограничении по эффекту встречи уменьшение бетатронной функции ведет к пропорциональному увеличению светимости. Важный вывод из этого замечания: выбор бетатронной функции определяется только требованиями со стороны детектора на протяженность области взаимодействия и техническими требованиями со стороны оптики кольца и ВЧ системы. Так, например, протяженность области взаимодействия при бетатронной функции равной 0.5 метров и оптимальной длине сгустка составляет примерно 75 см – 1 метр. Если детектор устраивает протяженность в 1.5 – 2 метра, то можно смело работать с * = 1 м. В светимости мы при этом ничего не потеряем, но выиграем в амплитуде ВЧ, необходимой для финальной группировки, и упростим задачу для разработчиков оптической структуры коллайдера. (В скобках стоит спросить, вслед за группой источника, а в чем все-таки прелесть урана, по сравнению с золотом или со свинцом, кроме того, что он ядовит и жутко неудобен для источника? Светимость по свинцу или золоту, при прочих равных условиях, примерно на 10% выше, чем по урану. Каков выигрыш по сечению при переходе на уран?) Из выражения (1.7) видно, что при прочих равных условиях, если светимость ограничена сдвигом бетатронного числа, то она больше в том коллайдере, у которого периметр меньше. Поэтому RHIC, с его примерно 3.8 км периметром, для NICA не конкурент – светимость на той же энергии будет как минимум примерно в 20 раз меньше. Это вполне очевидно, если принять во внимание, что N N c Trev C представляет собой линейную плотность частиц, которая может быть примерно постоянна при разной длине окружности. В случае с RHIC (а у них 90 – 120 сгустков на 2520 сепаратрисс) текущее значение линейной плотности еще раз в двадцать ниже, чем планируется в NICA, поэтому, без изменения процедуры заполнения кольца, они еще примерно в эти же 20 раз проигрывают по светимости, из-за большего периода обращения. Т.е. у проекта NICA на текущий момент фора в светимости по сравнению с RHIC на низкой энергии больше, чем два порядка. Один порядок RHIC может отыграть, если они заполнят сгустками весь периметр. 2. Применение охлаждения только на энергии инжекции и средняя светимость 2.1. Пиковая светимость Первый вопрос, на который нужно ответить, это: а можно ли достичь той пиковой светимости, о которой мы рассуждали, если охлаждать пучок на энергии инжекции, примерно равной 1 ГэВ/н и потом ускорять до энергии эксперимента? Вопрос вполне законный: если мы ограничены величиной сдвига бетатронного числа, то максимальный сдвиг мы должны получить именно на энергии эксперимента. Если мы охлаждаем на энергии инжекции, то при охлаждении мы все равно достигаем примерно той же величины сдвига бетатронного числа (мы ограничены той же клеткой на диаграмме). Дальше, при ускорении, сдвиг бетатронного числа уменьшается, и мы должны иметь возможность снова поднять его к порогу неустойчивости, но уже без применения охлаждения. Такая возможность действительно имеется, и она связана с тем, что сдвиг бетатронного числа можно увеличить, не уменьшая эмиттанса, за счет увеличения фактора группировки. При этом пропорционально возрастет разброс по импульсу, но он напрямую в выражение для светимости не входит. Возможные ограничения фактора группировки связаны с достижимой величиной амплитуды ВЧ напряжения и динамической апертурой по импульсному разбросу. 2.2. Номер гармоники Какой фактор группировки нам требуется? Или, иными словами, на какой гармонике частоты обращения мы собираемся группировать? Геометрическим ограничением номера гармоники сверху, служит требование избежать паразитных точек встречи сгустков в прямолинейной секции коллайдера, где находится точка встречи. За время пролета этой секции сгусток должен столкнуться со встречным сгустком только один раз в центре промежутка и не встретить в этой секции других сгустков. Встречные пучки сводятся и разводятся по вертикали дипольными магнитами, расположенными симметрично по обе стороны от точки встречи. Столкновение будет только одно, если расстояние между центрами соседних сгустков на длину сгустка больше, чем расстояние между дипольными магнитами Ld (Рис. 1): C / h Ld 2 s , (2.1) что при Ld ~ 10 м соответствует максимально допустимой гармонике примерно h 20. * Ld Рис. 1. Схематическое изображение прямолинейного участка с точкой встречи. При двадцатой гармонике (примерно 30 МГц) финальное значение фактора группировки примерно равно 13. Если начинать ускорение с фактора группировки, близкого к единице, то после ускорения, за счет адиабатического увеличения амплитуды ВЧ, можно поднять сдвиг бетатронного числа примерно на порядок. С учетом затухания эмиттанса сдвиг бетатронного числа при ускорении затухает примерно как 2, и повышение фактора группировки, в принципе, способно скомпенсировать этот эффект. 2.3. Эволюция светимости во время эксперимента Предполагая, что в процессе проведения эксперимента число частиц убывает в соответствии с характерным временем жизни пучка, а эмиттанс пучка увеличивается за счет внутрипучкового рассеяния (или уменьшается при применении охлаждения), время жизни светимости можно выразить через характерное время жизни пучка и характерное время изменения эмиттанса как: 1 dL 1 dN 1 d 2 . L dt N dt dt (2.2) В отсутствии электронного охлаждения потери частиц определяются рассеянием и перезарядкой на остаточном газе и ядерными реакциями в точке встречи (при электронном охлаждении доминирующим процессом является рекомбинация в секции охлаждения). Все эти процессы имеют характерные времена порядка нескольких суток (при проектном значении давления остаточного газа в камере), и, фактически, время жизни светимости определяется только ростом эмиттанса. Характерное время роста эмиттанса из-за многократного рассеяния составляет так же несколько суток, и единственный процесс, который ограничивает время жизни светимости это ВПР. Тогда: 1 dL 1 d 1 L dt dt IBS (2.3) Характерное время роста эмиттанса из-за ВПР само зависит от величины эмиттанса, поэтому уменьшение светимости со временем, описываемое формулой (2.3), оказывается существенно медленнее, чем экспоненциальное. Пояснить это можно на примере качественного описания ВПР, используя приближенную модель, в соответствии с которой 1 IBS D , 2 2 (2.4) где коэффициент диффузии D постоянен и определяется начальными значениями эмиттансов. Уравнение (2.2.2) дает правильную зависимость эмиттанса от времени – t 0 1 D 02 t - эмиттанс растет пропорционально корню квадратному из времени, что наблюдается в эксперименте. Подставив выражение (2.4) в уравнение (2.3) получим для светимости 1 dL DL2 , 2 L dt 2L (2.5) где произведение L введено в выражение для правой части, т.к. оно является константой для круглого пучка. Интегрируя уравнение (2.2.3) можно получить зависимость светимости от времени в явном виде: Lt L0 1 D 02 , (2.6) t где 0 – начальное значение эмиттанса, а L0 – соответствующее ему пиковое значение D 1 светимости, или, с учетом того, что представляет собой темп ВПР в 2 2 0 IBS ,0 начальный момент времени Lt L0 1 2t . (2.7) IBS , 0 Эта зависимость значительно слабее экспоненты, так, например, уменьшение светимости в е раз достигается при t 3.3 IBS,0, при экспоненциальной зависимости светимость уменьшилась бы за тот же промежуток времени в примерно 27 раз. В принципе, это позволяет проводить эксперимент в течение достаточного длительного времени без охлаждения и без существенного уменьшения светимости. 2.4. Пример параметров пучка и результаты моделирования Реалистическая численная оценка и времени эксперимента, и требуемого количества частиц (понятно, что светимость в начальный момент времени должна быть выше 10 27 см2с-1, и оценки требуемого числа частиц, приведенные в первом разделе, отвечают условию «заведомо не меньше, чем») после оценки окончательного выбора схемы работы коллайдера. Однако, для представления масштаба характерных времен, можно пока остановиться на параметрах пучка, приведенных в таблице 2.1. Число частиц выбрано в полтора раза большее, чем по минимальной оценке требуется на энергии 3.5 ГэВ/н. Это позволило несколько отодвинуться от порогов неустойчивостей. Горизонтальный и вертикальный эмиттанс выбраны таким образом, чтобы темпы роста фазового объема по всем трем степеням свободы были примерно равны, что соответствует условию термодинамического равновесия. При этом отсутствует релаксация сгустка и темпы нагрева минимальны. Таблица 2.1. Ориентировочные параметры пучка для оценки Полное число частиц в каждом из колец 31010 Энергия ГэВ/н 3.5 Номер гармоники 20 Бетатронная функция в точке встречи м 0.5 Среднеквадратичная длина сгустка м 0.55 Разброс по импульсу 10-3 ВЧ амплитуда кВ 200 Эмиттанс, хор/верт 0.65/0.36 мммрад Сдвиг бетатронного числа, хор/верт 0.016/0.021 «Бим-бим» параметр, хор/верт 0.0023/0.00314 -2 -1 Начальная светимость см с 1.51027 Разброс по импульсу является относительно свободным параметром, и, например, величине 10-3 при требуемой длине сгустка соответствует амплитуда ВЧ примерно равная 200 кВ. Если при финальной группировке, фактор группировки будет увеличен на порядок, то разброс по импульсу сразу после ускорения должен быть равен примерно 10-4. Номер гармоники выбран вблизи максимально допустимой величины как раз для того, чтобы иметь минимум амплитуды ВЧ. Снижение номера гармоники, потребует для обеспечения той же длины сгустка большей амплитуды. Длина сгустка выбрана как компромисс между эффектом песочных часов, требований динамики и параметров ВЧ системы. При длине 55 см светимость составляет примерно 60 % от величины, определяемой формулой (1.1). Моделирование динамики проводилось для структуры, представленной на Рис. 2. Начальные темпы ВПР составляют примерно 0.01 с-1. Рис. 2. Структурные функции коллайдера NICA, использованные в расчетах Пример расчета эволюции эмиттанса и длины сгустка в процессе эксперимента представлены на Рис.3 Рис. 3. Эмиттансы и длина сгустка как функции времени. Светимость при этом снижается за 200 с до величины примерно 0.751027 см-2с-1. Средняя величина за 200 с примерно равна 1027 см-2с-1. Примерно после 200 с необходимо провести охлаждение пучка: эмиттанс уменьшить примерно в два раза в обеих плоскостях, а разброс по импульсу примерно в полтора. Рис. 4. Светимось как функция времени.