изгиб балок - Балаковский Институт Техники, Технологии и

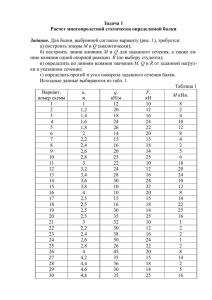
Апробация
Министерство образования и науки Российской Федерации
Национальный исследовательский ядерный университет «МИФИ»
Балаковский инженерно-технологический институт
ИЗГИБ БАЛОК
Методические указания
к выполнению лабораторных работ
по курсу «Сопротивление материалов»
для студентов механических и строительных
специальностей и направлений очной и заочной форм обучения
Одобрено
редакционно-издательским советом
Балаковского инженерно-технологического
института
Балаково 2016
ВВЕДЕНИЕ
В методические указания включены руководства к трем лабораторным работам, относящимся к изгибу балок. Эти работы объединены в цикл
лабораторных работ в связи с тем, что они охватывают один объект
изучения (балки при изгибе) и связаны единой методикой измерения.
Поэтому разделы «МЕТОДИКА ЭКСПЕРИМЕНТА», «ТЕХНИКА БЕЗОПАСНОСТИ», общие для всех работ, вынесены в начало данных
методических указаний.
Лабораторные работы выполняются звеньями по 3-4 человека в часы,
предусмотренные расписанием учебных занятий. За одну - две недели до
выполнения лабораторной работы студент должен ознакомиться по
настоящему руководству со всеми разделами работы и на собеседовании с
преподавателем показать свою достаточную подготовленность к выполнению работы. После выполнения работы студент должен представить письменный отчет по работе. Отчет должен быть оформлен в ученической
тетради; схемы, чертежи, таблицы должны быть выполнены с использованием чертежных инструментов. Отчет должен содержать пункты,
указанные в разделе «СОДЕРЖАНИЕ ОТЧЕТА ПО РАБОТЕ».
МЕТОДИКА ЭКСПЕРИМЕНТА
Описание лабораторной установки
Лабораторная установка СМ4А, показанная на рис.1, состоит из
следующих частей: исследуемого стального образца балки 10; основания 1,
установленного на четырех регулируемых винтах-ножках 11; левой 5 и
правой 12 стоек; индикаторной стойки 6; гиревого подвеса 9; набора
грузов 8. Модуль упругости материала балки =2,1х105 МПа. Балка имеет
прямоугольное поперечное сечение шириной b=39,0 мм, высотой h=7,0 мм.
Балка установлена на шарнирные опоры, расположенные на стойках
5 и 12 и закреплена на осях вращения опор с помощью прижимных планок
2
и винтов. С осью вращения каждой опоры жестко связан стержень 4,
имеющий на конце пятку 2, в которую упирается наконечник индикатора
13. Этот индикатор служит для измерения угла поворота опорного
сечения. Расстояние от наконечника индикатора до нейтрального слоя
балки образца L=150 мм. Правая опора неподвижно закреплена на стойке
12. Левая опора, закрепленная на стойке 5, является шарнирно-подвижной
опорой. Стойка 5 имеет возможность перемещаться вдоль основания,
позволяя тем самым менять длину пролета балки. Индикаторные стойки 6
и гиревые подвесы 9 могут перемещаться вдоль балки. Для определения
положения грузов и индикаторов на балке имеется дециметровая шкала.
Рис.1
Методика измерений
Линейные перемещения (прогибы балки) измеряются путем прямых
измерений методом непосредственной оценки по шкале индикатора.
Угловые перемещения определяются путем косвенных измерений.
При этом методом непосредственной оценки по шкале индикатора
измеряется горизонтальное перемещение X пятки стержня 4 (см. рис.1 и
рис.2), а угол поворота определяется из соотношения   tg 
3
X
(1). Силы,
L
действующие на балку, определяются количеством мер (гирь), установленных на грузовые подвесы.
Рис. 2
Опорная реакция измеряется с помощью динамометра ДПУ-0,02-2.
Значения длин участков балки могут быть установлены на шкале,
нанесенной на самом образце.
Описание измерительных средств
Индикатор часового типа ИЧ-10. Индикатор предназначен для
определения линейных перемещений. На рис.3 показан внешний вид
индикатора. Штифт 2 с наконечником 1 связан со стрелками 4 и 6
системой зубчатых передач. Пружиной измерительный наконечник
прижимается к поверхности, перемещение которой в направлении штифта
нужно измерить. Корпус 3 индикатора поддерживается неподвижно
особым штативом. Перемещение поверхности 9 вызывает перемещение
штифта 2, который вращает стрелки 4 и 6.
Одно деление шкалы 5 соответствует перемещению измерительного
наконечника равному 1 мм. Эта шкала имеет 10 делений. Шкала 7 имеет
100 делений с ценой 0,01 мм. Для установки стрелки 6 индикатора на нуль
шкалу 7 следует повернуть, вращая ободок 8. Шкала 7 – двойная: черная
шкала
используется
для
измерения
4
перемещений
поверхности
9,
направленных к корпусу индикатора; красная шкала используется при
измерении перемещений в обратном направлении.
Динамометр ДПУ-0,02-2. Динамометр предназначен для измерения
статических растягивающих усилий в пределах от 0 до 0,2 кН. Общий вид
динамометра показан на рис. 4. Динамометр работает по принципу
определения силы по значению деформации упругого элемента, которая
через рычажный передаточный механизм преобразуется в показания по
указателю (стрелке) 4 и шкале 5. Усилия передаются на динамометр через
серьги 3. Для установки шкалы 5 в нулевое положение при отсутствии
нагрузки на динамометр следует повернуть обод 2 в нужном направлении,
ослабив предварительно винт 1 и снова закрепив его после поворота обода.
Рис.3
Рис.4
ПРАВИЛА ТЕХНИКИ БЕЗОПАСНОСТИ
При выполнении работы единственной опасностью является падение
грузов с гиревых подвесов. Поэтому необходимо соблюдать следующие
меры предосторожности.
1. Гири устанавливать на подвесы плавно, без удара.
5
2. Следить, чтобы прорезь последующего груза находилась в другой
плоскости по отношению к прорези предыдущего груза.
3. Запрещается нагружать подвесы грузом массой более 6 кг.
Лабораторная работа№5
ОПРЕДЕЛЕНИЕ ПРОГИБОВ И УГЛОВ ПОВОРОТА СЕЧЕНИЙ
БАЛКИ ПРИ ИЗГИБЕ
Ц е л ь р а б о т ы : определить опытным путем величину прогиба и
угла поворота сечений балки и сравнить их с величинами, полученными
теоретическим расчетом.
ОСНОВНЫЕ ПОНЯТИЯ
Под действием внешних сил балка деформируется таким образом,
что ее геометрическая ось искривляется. Изогнутую ось балки называют
упругой линией. Если поперечное сечение балки имеет ось симметрии и
все внешние силы действуют в плоскости симметрии, то упругая линия
будет располагаться в этой же плоскости симметрии. Такой случай изгиба
бруса называется прямым изгибом. При прямом изгибе перемещения
произвольного сечения балки (рис.5) характеризуется двумя величинами:
прогибом w и углом поворота φ.
Рис.5
Прогибом называется перемещение центра тяжести поперечного
сечения в направлении, перпендикулярном геометрической оси балки до
деформации.
6
Углом поворота сечения (девиацией сечения) называется угол, на
который поворачивается поперечное сечение по отношению к положению
сечения до деформации.
Теоретически прогиб и угол поворота можно определить методом Мора
с применением правила Верещагина. Методика определения перемещений
с помощью интеграла Мора студентам известна. Прежде чем продолжить
изучение настоящего руководства:
1. Запишите интеграл Мора для определения перемещений при изгибе.
2. Вспомните, как вычисляется интеграл Мора по правилу Верещагина.
3. Ответьте на вопрос: в чем различие в применении метода Мора к
определению линейных и угловых перемещений.
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
Задание 1
Экспериментальное определение прогибов и углов поворота.
Оборудование и принадлежности:
Лабораторная установка, описание которой приведено в разделе
МЕТОДИКА ЭКСПЕРИМЕНТА.
1. Подготовить установку для выполнения эксперимента, установив
подвижную опору, подвесы для грузов и индикатор 1 в соответствии с
вариантом задания, указанным преподавателем. Схема расположения
нагрузок и индикаторов для выбора задания показана на рис.6; варианты
задания приведены в табл. 1.
Рис.6
7
Таблица 1
Варианты заданий
№
a, см
c, см
d, см
P, H
1
10
20
40
9,8
2
20
40
50
9,8
3
30
60
10
14,7
4
30
70
20
14,7
5
40
80
30
14,7
6
40
70
30
19,6
7
0
30
50
14,7
8
0
30
60
14,7
9
0
40
70
14,7
10
0
40
40
14,7
11
20
40
40
19,6
12
20
60
40
14,7
13
0
30
50
9,8
14
0
30
40
9,8
15
30
40
50
19,6
варианта
Закрепить штативы индикаторов 1 и 2 и подвижную опору к основанию
установки, а подвесы для грузов – к образцу, с помощью имеющихся на
них винтов. Убедиться в том, что стойки индикаторов надежно закреплены, без люфтов, что оси измерительных штифтов расположены перпендикулярно поверхности, перемещение которой определяется.
2. Индикаторы закрепить так, чтобы стрелка малой шкалы находилась
в среднем положении, указанном цифрой 5. Стрелку большой шкалы
выставить на 0 или близкое к 0 значение. Нагружая рукой подвес, к
которому должна прикладываться нагрузка, установить направление
вращения стрелки большой шкалы каждого индикатора. При повороте ее
8
по часовой стрелке показания следует снимать по черной шкале, при
вращении стрелки в обратном направлении – по красной.
3. Подготовить таблицу для записи показаний при испытании по
следующей форме (табл. 2).
Отсчеты по индикаторам следует записывать с точностью до 1 деления
шкалы.
4. При отсутствии нагрузки записать в табл. 2 отсчеты Z1, Z2 по двум
индикаторам.
Таблица 2
Таблица результатов наблюдений
Отсчеты по шкале индикатора
Нагрузка
индикатор 1
Z1
индикатор 2
X1
O
P
2P
3P
4P
3P
2P
P
O
9
Z2
X2
5. Нагружая балку гирями массой 1,0; 1.5 или 2,0 кг в соответствии с
заданием (гири на подвесы следует устанавливать осторожно, статически,
не допуская ударов), а затем разгружая ее, записать на каждой ступени
нагружения отсчеты по индикаторам в табл. 2.
6. Вычислить разности смежных отсчетов X1,X2, которые определяются
как разность последующего и предыдущего отсчетов при нагружении и
разности предыдущего и последующего отсчета при разгрузке и записать в
соответствующие столбцы табл.2.
7. Провести анализ полученных результатов. Если в каком-либо
столбце Xϊ окажутся значения, выпадающие из общего ряда, т.е.
значительно отличающиеся от других значений этого столбца, то эти
значения следует исключить из дальнейшей обработки или повторить
измерения.
8. Провести обработку результатов, полученных в табл.2.
Прогиб балки w определяется прямым измерением с многократными
наблюдениями индикатора 1 (см. рис. 6).
Результат измерения прогиба определяется формулой
c n
w   X1i ,
n i 1
где
с
= 0,01 мм – цена деления индикатора;
i
-
порядковый номер наблюдений;
n
-
число наблюдений;
X1i -
(2)
разность смежных отсчетов по индикатору 1.
Угол поворота сечения на правой опоре φ определяется путем
косвенного измерения индикатором 2 и находится по формуле
c n

X 2i ,

nL i 1
10
(3)
где
X1i L
разность смежных отсчетов по индикатору 2,
= 150 мм – результат измерения расстояния от наконечника
индикатора 2 до центра тяжести сечения.
Остальные обозначения те же, что и в формуле (2). Результат вычислений
прогиба w должен быть округлен с точностью до 0,01 мм, угла поворота
сечения φ до 0,01 рад.
Задание 2
Теоретический расчет перемещений и сравнение результатов
расчета с результатами эксперимента
Теоретический расчет рекомендуется производить с помощью
интеграла Мора в следующем порядке.
1. Начертить расчетную схему балки – образца с указанием всех
размеров и нагрузок и построить эпюру изгибающих моментов Мр .
2. Начертить схему вспомогательного единичного состояния для
определения перемещения в сечении, где установлен индикатор 1.
Построить эпюру изгибающих моментов М 1 для этого состояния. В
качестве примера на рис.7 показаны расчетные схемы и эпюра
изгибающих моментов для варианта 15 (см. табл. 1): а) и б) расчетная
схема и эпюры изгибающих моментов для заданного грузового состояния
балки; в) и г) схема и эпюра изгибающих моментов вспомогательного
состояния, необходимого для определения прогиба в точке 1 (индикатор
1); д) и е) схема и эпюра изгибающего момента вспомогательного
состояния для определения угла поворота на правой опоре (индикатор 2).
3. Записать в тетрадь отчета значения модуля упругости балки Е в H/м2
и размеры поперечного сечения в м. Вычислить момент инерции
поперечного сечения балки
11
b  h3
Iy 
12
, м4
(4)
Рис.7
Результат округлить до 4-х значащих цифр.
4. Интеграл Мора для определения перемещений при изгибе балок
имеет вид:
l
 ip  
0
Mp Mi
E  Iy
dx,
где,  ip - определяемое перемещение – прогиб или угол поворота;
12
(5)
Мр
-
изгибающий момент в произвольном сечении балки от
заданной нагрузки;
Мi -
изгибающий момент в произвольном сечении балки для
соответствующего вспомогательного единичного состояния.
Интегрирование ведется по всей длине балки l. Ввиду того, что на
разных участках балки изгибающие моменты описываются различными
аналитическими выражениями, интеграл по l определяется как сумма
интегралов, вычисленных по отдельным участкам балки. Поэтому, прежде
чем производить вычисление по формуле (см выше), следует разбить балку
на участки так, чтобы в пределах каждого участка эпюры Мр и
М i изображались прямыми линиями (см. рис.6). Интеграл Мора для
участка длиной li, показанного на рис.8, следует вычислять по формуле
перемножения эпюр, имеющих вид трапеций:
l

0
M p  Mi
E  Iy
dx 
li
 2a p  a i  2b p  bi  a p  bi  a i  b p 
6E  I y
(6)
Рис. 8
При определении прогиба ∆ip для балки, показанной на рис.7,
вычисления следует провести для двух участков a1 и a2, т.к.на участке «a»
13
одна из эпюр нулевая, при вычислении угла поворота φ – для одного
участка длиной a1 + a2.
1
1  0,3
2  4,41 0  2  2,52  0,171  2,52  0 
w  ip 
M p  M1dx 

E  Iy 0
E  I y  6
l


0,4
 2  2,52  0,171  2  0  0  2,52  0  0  0  0,171   0,1353 H  м3
6
E  Iy

l
1
1

M

M
2 dx 
p
E  I y 0
E  Iy

0,5145
 0,7



2

4
,
41

0

2

0

1

4
,
41

1

0

0


 6

E  Iy
[Hм2]
Окончательные результаты теоретического расчета следует округлять
до двух значащих цифр.
5. Сравнить
результаты
теоретического
расчета
с
результатами
эксперимента в таблице 3.
Таблица 3
Обозначения
Результаты расчета
Результаты
величин
Разница в %
эксперимента
w
φ
Разница подсчитывается по выражению
ТЭ
100 %,
Э
(7)
где Т – результат теоретического расчета;
Э – результаты измерений.
6. Сделать выводы по работе. Можно считать, что теория изгиба
удовлетворительно согласуется с опытом, если разница не превышает 5%.
14
СОДЕРЖАНИЕ ОТЧЕТА ПО РАБОТЕ
Отчет по работе должен содержать:
1. Название работы.
2. Цель работы.
3. Расчетную схему балки.
4. Запись результатов испытаний (табл. 2).
5. Обработку экспериментальных данных.
6. Теоретический расчет прогибов и углов поворота.
7. Таблицу сравнения результатов эксперимента и расчета.
8. Выводы.
В разделе отчета «Выводы» должно быть указано, согласуется или не
согласуется теория с результатами эксперимента.
ВОПРОСЫ ДЛЯ САМОПРОВЕРКИ
1. Назовите, какими перемещениями характеризуются деформации
балки при прямом изгибе?
2. Какие приборы используются для определения перемещений?
3. Как измеряются углы поворота сечения?
Время, отведенное на лабораторную работу
Подготовка к работе
0,5 акад. часа.
Выполнение работы
2,5 акад. часа.
Обработка результатов эксперимента
1,0 акад. час.
и оформление отчета
15
Лабораторная работа№6
ОПЫТНАЯ ПРОВЕРКА ТЕОРЕМ О ВЗАИМНОСТИ РАБОТ И О
ВЗАИМНОСТИ ПЕРЕМЕЩЕНИЙ
Цель работы:
экспериментально проверить справедливость теорем
о взаимности работ и о взаимности перемещений.
ОСНОВНЫЕ ПОНЯТИЯ
Теоремы о взаимности работ и о взаимности перемещений имеют
большое значение в сопротивлении материалов и строительной механике
при исследовании напряженного и деформированного состояния линейнодеформируемых систем.
Рассмотрим кратко формулировку этих теорем.
Рассмотрим два состояния упругой системы, находящейся в
равновесии. В первом состоянии (1) на систему действует только сила Р1, а
во втором (2) только сила Р2 (рис. 9).
(1)
(2)
Рис. 9
Перемещение упругой системы будем обозначать символом mn, где
первый индекс m указывает направление перемещения, а второй n
16
причину, вызвавшую его. Таким образом, mn – перемещение по
направлению силы m, вызванное силой n.
Работу силы Р1 на вызванном ею перемещении 11 будем обозначать
W11, а работу силы Р2 на вызванном ею перемещении 22 – W22.
При статическом действии сил Р1 и Р2 будем иметь:
W11 
1
P1  11 ;
2
W22 
1
P2  22 .
2
Рассмотрим теперь случай статического нагружения той же системы
силами Р1 и Р2 (рис. 10) в следующей последовательности
Рис. 10
Сначала к системе прикладывается статически нарастающая сила Р1.
После того как процесс деформации системы от силы Р1 закончится, к
системе прикладывается также статически нарастающая сила Р2.
Полная работа, совершенная силами Р1 и Р2, в процессе деформации
будет состоять из 3-х частей.
1. Работа силы Р1 на вызванном ею перемещении 11
W11 
1
P111 .
2
2. Работа силы Р2 на вызванном ею перемещении 22
W22 
1
P2  22 .
2
3. Работа силы Р1 на перемещении 12, вызванном действием силы Р2
W12  P112 .
17
Полная работа будет равна сумме этих работ
W 
1
1
P111  P2  22  P112 .
2
2
Если теперь упругую систему загрузить в обратном порядке, то есть
если сначала приложить статически силу Р2 и после окончания процесса
деформации приложить статически силу Р1 , то совершенно аналогично
найдем полную работу
W 
1
1
P111  P2  22  P2  21 .
2
2
Так как работа W зависит только от конечных значений сил и
перемещений и не зависит от порядка нагружения, приравнивая правые
части двух последних уравнений, получим
P112  P2  21
или
W12  W21
(8)
Такой же результат можно было получить, если бы в каждом из
рассматриваемых состояний прикладывалась не одна сила, а любое число
сил и моментов.
Таким образом, работа сил первого состояния на перемещениях по
их направлению, вызванных силами второго состояния, равна работе сил
второго состояния на перемещениях по их направлению, вызванных
силами первого состояния. Этот вывод носит название теоремы о
взаимности работ.
Перемещения в упругой системе, вызванные действием единичных
сил, будем обозначать символом  в отличие от символа  , которым
обозначались перемещения от действия сил, не равных единице. Индексы
при  имеют тот же смысл, что и ранее.
Если теперь рассмотреть два состояния упругой системы, в которых
к системам прикладываются единичные силы, то на основании теоремы о
взаимности работ (8), полагая
18
12  12 ,
P1  P2  1 , а
 21  21
получим теорему о взаимности перемещений
12   21
(9)
Эту теорему можно сформулировать следующим образом. Для двух
единичных состояний упругой системы перемещение по направлению
первой единичной силы, вызванное второй единичной силой, равно
перемещению по направлению второй силы, вызванному первой силой.
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
Задание 1
Экспериментальная проверка теоремы о взаимности работ и
взаимности перемещений
Оборудование
и
п р и н а д л е ж н о с т и : лабораторная
установка, описание которой дано в разделе «МЕТОДИКА ЭКСПЕРИМЕНТА»
1. Подготовить лабораторную установку к выполнению работы,
установив подвижную опору и подвески для грузов в соответствии с
вариантом задания, указанным преподавателем. Схема балки для выбора
задания дана на рис. 11, а варианты задания – в табл. 4.
Рис. 11
19
Таблица 4
Варианты заданий
№
l, м
а, м
с, м
Р1, Н
Р2, Н
1
0,70
0,30
0,30
19,6
9,8
2
0,70
0,30
0,40
19,6
9,8
3
0,70
0,30
0,50
19,6
9,8
4
0,80
0,20
0,30
19,6
9,8
5
0,80
0,20
0,40
19,6
9,8
6
0,80
0,20
0,50
19,6
9,8
7
0,70
0,20
0,30
19,6
9,8
8
0,70
0,20
0,40
19,6
9,8
9
0,70
0,20
0,50
19,6
9,8
10
0,70
0,30
0,35
9,8
19,6
варианта
2. Установить индикаторы для измерения перемещений в сечениях, где
установлены подвески для грузов Р1 и Р2 . Проверить надежность
крепления индикаторных стоек.
3. Установить стрелки индикаторов 1 и 2 на нуль.
4. Нагрузить балку силой Р1 и по индикатору 2 записать отсчет Х21 .
Разгрузить балку. Нагрузить балку силой Р2 и снять отсчет Х12 . Отсчеты
по индикаторам следует снимать с точностью до одного деления шкалы.
5. Произвести обработку результатов измерений в соответствии с
разделом «Обработка результатов эксперимента».
ОБРАБОТКА РЕЗУЛЬТАТОВ ЭКСПЕРИМЕНТА
Перемещения сечений балки 21 и 12 определяются по формулам:
 21  X 21  c ;
где Х21 и Х12
12  X12  c ,
– отсчеты по индикаторам 2 и 1 соответственно,
С = 0,01мм – цена деления индикатора.
20
Обработку результатов эксперимента следует проводить в такой
последовательности.
1. Определить перемещения 21 и 12 по формулам
 21  X 21  cмм ; 12  X12  cмм  ,
где Х21 и Х12 – отсчеты по индикаторам 2 и I соответственно, С = 0,01мм –
цена деления индикатора.
2. Вычислить возможные работы W21 и W12
W21  P2  21 103 Дж  ; W12  P112 103 Дж  .
3. Подставить найденные значения работ в формулу (8) и сравнить
левые и правые части, определив погрешность по формуле:
W 
| W21  W12 |
100% .
W12
4. Теорему о взаимности работ можно считать экспериментально
подтвержденной, если погрешность W не превышает 5%
5. Определить единичные перемещения 21 и 12 по формулам:
 21 


 21 мм
Н ;
P1
 12 


12 мм
Н .
P2
6. Подставить найденные значения единичных перемещений в формулу
(9) и сравнить левые и правые части, определив погрешность по формуле:
 
|  21   12 |
 12
 100% .
Теорему о взаимности перемещений можно считать экспериментально
подтвержденной, если погрешность  не превышает 5%.
21
СОДЕРЖАНИЕ ОТЧЕТА ПО РАБОТЕ
Отчет по работе должен содержать:
1. Название работы.
2. Формулировку цели работы.
3. Формулировку теорем о взаимности работ и взаимности перемещений.
4. Схему установки в соответствии с указанным вариантом задания.
5. Результаты наблюдений.
6. Окончательные результаты.
7. Выводы.
ВОПРОСЫ ДЛЯ САМОПРОВЕРКИ
1. Сформулируйте теоремы о взаимности работ и о взаимности
перемещений.
2. Как экспериментально определяется работа W12 и W21?
3. Опишите, как производится измерение перемещений 12 и 21.
4. Каким образом экспериментально определяются единичные перемещения 12 и 21?
Время, отведенное на лабораторную работу
Подготовка к работе
1,0 акад. час.
Выполнение работы
0,25 акад. часа.
Обработка результатов эксперимента
0,75 акад. часа.
и оформление отчета
22
Лабораторная работа№7
ОПРЕДЕЛЕНИЕ РЕАКЦИИ СТАТИЧЕСКИ НЕОПРЕДЕЛИМОЙ
БАЛКИ
Ц е л ь р а б о т ы : определить опытным путем реакцию статически
неопределимой балки и сравнить полученный результат с результатом
теоретического расчета.
ОСНОВНЫЕ ПОНЯТИЯ
Статически неопределимыми называются системы, в которых реакции
опор и внутренние силовые факторы невозможно определить из уравнений
равновесия. Отличительной особенностью таких систем является наличие
в них связей, которые можно удалить, не нарушая кинематическую
неизменяемость системы. Эти связи принято называть лишними. Статическая неопределимость будет раскрыта, если реакции лишних связей будут
каким-то образом определены.
Одним из методов расчета статически неопределимых систем является
метод сил, с которым студенты уже знакомы. Поэтому, прежде чем
приступить к выполнению работы, вспомните:
1. Как определяется степень статической неопределимости?
2. Что такое основная система?
3. Как записываются канонические уравнения метода сил?
4. Какие величины являются неизвестными в этих уравнениях?
5. Какой геометрический смысл этих уравнений?
6. Как определяются коэффициенты канонических уравнений?
При необходимости обратитесь к учебникам [1], [2].
При экспериментальном определении опорной реакции статически
неопределимой балки на лабораторной установке воспроизводится основная система, полученная путем удаления опоры, реакцию которой требует-
23
ся определить. Реакция определяется из условия равенства нулю перемещения по направлению отброшенной опорной связи.
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
Задание 1
Экспериментальное определение опорной реакции статически
неопределимой балки
О б о р у д о в а н и е и п р и н а д л е ж н о с т и : лабораторная
установка СМ4А, динамометр ДПУ-0,02-2, описание которых дано в
разделе «МЕТОДИКА ЭКСПЕРИМЕНТА».
1. Вычертить схему заданной статически неопределимой балки в
соответствии с вариантом задания, указанным преподавателем. Схема
балки для выбора варианта задания приведена на рис. 12, а варианты
задания в табл. 5.
Рис.12
Примечание: во всех вариантах требуется определить реакцию опоры С.
2. Подготовить лабораторную установку к работе, для чего: установить
подвижную опору А (рис.12), как указано на рисунке; в сечении, где
приложена сила Р, установить подвес для гирь; в сечении, где расположена
опора С, установить индикатор и подвес для груза; закрепить подвижную
опору и стойку индикатора, подвески и убедиться в надежности их
крепления.
24
Таблица 5
Вариант задания
a,м
b, м
P, Н
1
0
0,70
9,8
2
0
0,60
19,6
3
0
0,60
19,6
4
0
0,80
29,4
5
0,5
0
19,6
6
0,6
0
19,6
7
0,7
0
9,8
8
0,8
0
29,4
9
0,4
0
14,7
10
0,2
0
14,7
3. При отсутствии нагрузки Р установить стрелку индикатора на нуль.
4. Приложить к балке силу Р, установив на гиревой подвес
необходимое количество гирь.
5. На подвеску в сечении С установить поддон для груза. Постепенно
нагружая поддон песком или дробью, увеличивать нагрузку до тех пор,
пока стрелка индикатора не вернется в исходное положение. Искомая
реакция опоры С будет равна весу поддона с грузом.
6. Снять поддон с грузом, повесить его на нижнюю серьгу динамометра, установленного на стене в лаборатории, по шкале динамометра
определить значение реакции опоры Rс.
Задание 2
Теоретическое определение реакции и сравнение результатов теории и
эксперимента
1. Вычертить основную систему заданной статически неопределимой
балки. На схеме показать силу Р, а действие отброшенной опоры заменить
неизвестной реакцией.
25
2. Записать каноническое уравнение метода сил
111  1P  0 .
(10)
3. Вычертить схемы грузового и единичного состояний основной
системы и построить опоры изгибающих моментов для этих состояний M P
и M1 .
4. Вычислить коэффициенты канонических уравнений по формулам
Мора
l
M P M1
dx ,
EJ
(11)
M1 M1
dx .
EJ
(12)
1P   0 
l
11   0 
Для вычисления интегралов, входящих в формулы (11) и (12), следует
использовать формулу трапеций.
5. Из уравнения (10) найти неизвестную реакцию.
6. Сравнить теоретическое и экспериментальное значение реакции и
сделать выводы по работе. Можно считать, что теория согласуется с
экспериментом, если разница между результатом теоретического расчета и
результатом измерения не превышает 5%.
СОДЕРЖАНИЕ ОТЧЕТА ПО РАБОТЕ
Отчет по работе должен содержать:
1. Название работы.
2. Формулировку цели работы.
3. Схему заданной статически неопределимой балки.
4. Результаты измерения опорной реакции.
5. Теоретический расчет.
6. Выводы.
26
ВОПРОСЫ ДЛЯ САМОПРОВЕРКИ
1. Как экспериментально определяется опорная реакция статически
неопределимой балки?
2. Какой прибор используется для измерения реакции? На каком
принципе основывается его действие?
Время, отведенное на лабораторную работу
Подготовка к работе
0,5 акад. часа.
Выполнение работы
1 акад. час.
Оформление отчета
0,5 акад. часа.
ЛИТЕРАТУРА
1. Феодосьев В.И. Сопротивление материалов: учебник для втузов. –
11-е изд. – М.: Изд-во МГТУ им. Н.Э. Баумана, 2003. – 592 с. (§5.3§5.6, с. 235-258; §6.1-§6.3, с. 259-277).
2. Александров А.В., Потапов В.Д., Державин Б.П. Сопротивление
материалов. – 4-е изд., испр. – М.: Высш. шк., 2004. – 560с. (§8.9, с.
– 245-255; §9.1-9.3, с. 256-267).
СОДЕРЖАНИЕ
Введение ……..…………………………………………………………. 2
Методика эксперимента ………….…………………………………… 2
Правила техники безопасности ……………………………………… 5
Лабораторная работа №5 ……………………………………………… 6
Лабораторная работа №6 …………………………………………… 16
Лабораторная работа №7 ………………………………………..…… 23
Литература ……………………………………………………….…… 27
27
28