Олимпиада 2015 Решения задач
реклама
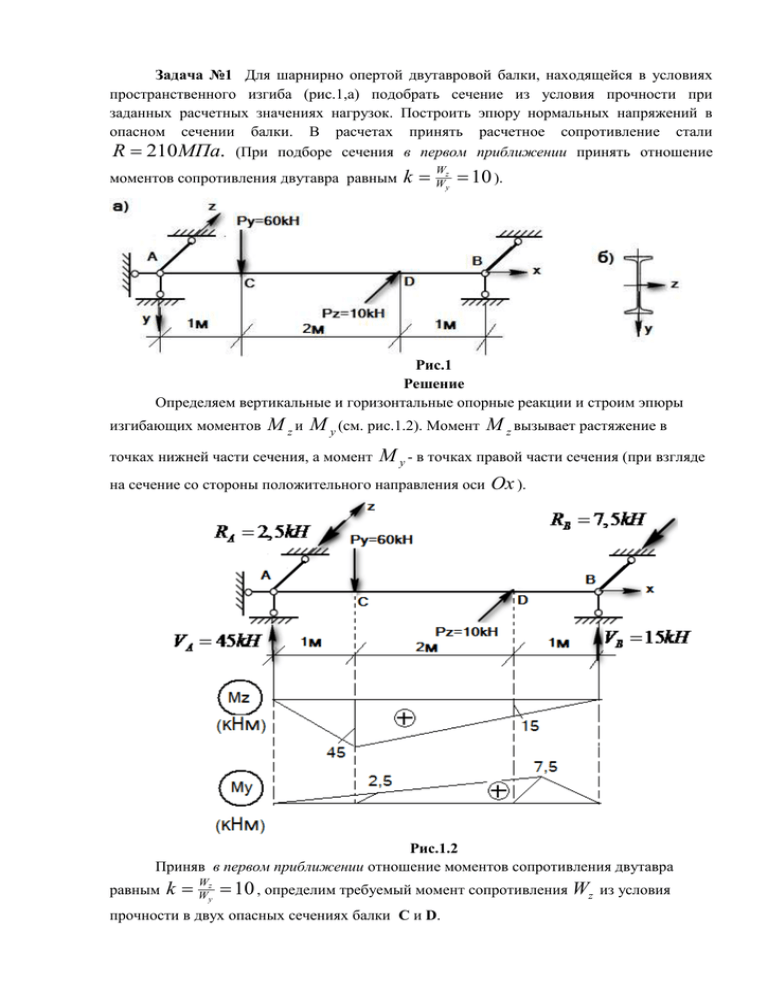
Задача №1 Для шарнирно опертой двутавровой балки, находящейся в условиях пространственного изгиба (рис.1,а) подобрать сечение из условия прочности при заданных расчетных значениях нагрузок. Построить эпюру нормальных напряжений в опасном сечении балки. В расчетах принять расчетное сопротивление стали R 210МПа. (При подборе сечения в первом приближении принять отношение моментов сопротивления двутавра равным k WWyz 10 ). Рис.1 Решение Определяем вертикальные и горизонтальные опорные реакции и строим эпюры изгибающих моментов M z и M y (см. рис.1.2). Момент M z вызывает растяжение в M y - в точках правой части сечения (при взгляде на сечение со стороны положительного направления оси Ox ). точках нижней части сечения, а момент Рис.1.2 Приняв в первом приближении отношение моментов сопротивления двутавра равным k WWyz 10 , определим требуемый момент сопротивления Wz прочности в двух опасных сечениях балки С и D. из условия Сечение С: Wz k Wy , x M Mz My Mz R, y R, Wz Wy k Wy Wy 1 Mz (45 / 10 2,5) 106 1 Mz ( M y ) R , Wy ( My) 33,33см3 . 3 Wy k R k 210 10 1 Mz (15 / 10 7,5) 106 Сечение D: Wy ( My) 42,86см3 . 3 R k 210 10 Более опасным является сечение D. По сортаменту принимаем двутавр №30, Wz 472см3 , Wy 49,9см3 . Определяем наибольшие напряжения в угловых точках двутавра сечения D и проверяем прочность балки 15 103 7,5 max 182MПа R 210МПа . 472 106 49,9 Прочность балки обеспечена с запасом, поэтому во втором приближении примем двутавр №27 Wz 371см3 , Wy 41,5см3 . Определяем наибольшие напряжения в угловых точках двутавра сечения D и проверяем прочность балки 15 103 7,5 max 221,2MПа R 210МПа . 371 106 41,5 Прочность балки не обеспечена (превышение 5,2%). Принимаем двутавр №30. Определим угол наклона нейтральной линии к оси Оz ( x M Mz y y z 0 ), Jz Jy Jz M y 7080 7,5 10,5 , 0 84,60 Jy Mz 337 15 как 0 0 ,то нулевая линия проходит через вторую и четвертую четверти осей tg ( 0 ) Так координат поперечного сечения. Эпюра нормальных напряжений приведена на рис.1.3 Рис.1.3 Задача №2 Колонна промышленного здания нагружена вертикальной силой Fх 600kH и горизонтальной Fy 4kH . Найти наибольшие сжимающие и растягивающие напряжения. Построить эпюру нормальных напряжений. Рис.2 Решение Fх , Fz , M z Приведем силы в центр тяжести сечения (рис. 2.1) Построим эпюры N ,M z,My (рис.2,1 ). Опасным сечением является сечение в заделке, а действующие в нем внутренние усилия равны: N Fx 600кН ; M y 600 0,06 36кНм (сжимают точки сечения в первой четверти); M z Fx l 4 3 12кНм (растягивают точки сечения в первой четверти); Рис.2,1 Геометрические характеристики сечения: A 0,3 0, 4 0,12 м 2 0,43 0,3 0,42 0,3 4 4 Jy 16 10 м ; Wy 8 103 м3 ; 12 6 3 0,4 0,3 0,4 0,32 4 4 Jz 9 10 м ; Wz 6 103 м3 . 12 6 Выражение для нормальных напряжений в произвольной точке сечения My N Mz 600 103 12 103 36 103 x y z y z, A Jz Jy 0,12 9 104 16 104 40 x (5 y 2, 25 z ) 3 Уравнение нейтральной линии x 0 . Определяем отрезки, которые отсекает нейтральная линия, на главных центральных осях инерции определяем из уравнения 40 yn 22,5 zn 0 . 3 15 zn 0, y n 0,375м . zn 40 5 Получаем: yn 0, zn 5 0, 22м 22,5 На рис. 2.2 Показана эпюра нормальных напряжений в точках сечения Рис.2.2 Задача №3 Стальной стержень длиной силой Py l 1м круглого сечения нагружен вертикальной 1,6kH , горизонтальной силой Pz 2, 4kH и моментом M x 2кНм (рис.3). Допускаемое напряжение стали 160МПа . 1) Определить диаметр стержня D из условия прочности ( i наибольших касательных напряжений ( i 2 4 2 ) ) по теории и по энергетической теории ( i 2 3 2 ). Касательные напряжения от поперечного изгиба при оценке прочности не учитывать. 2) Построить эпюру нормальных и касательных напряжений в опасном сечении стержня. Рис.3.1 Решение Геометрические характеристики круглого сечения: Wy Wz W D3 32 ;Wx D3 16 2 W . Опасным является сечение стержня в заделке. Определяем опорные реакции и вычисляем внутренние усилия в т.О. Значения внутренних усилий: M x 2кНм ; M z Py l 1,6кНм ; M y Pz l 2,4кНм . Вычисляем величину суммарного изгибающего момента M M M 2 z 2 y 2 l Pz2 Py2 1 1,62 2,42 2,88кНм . Наибольшие нормальные напряжения от M в двух точках контура круга x M W Касательные напряжения от крутящего момента максимальны в точках контура круга Mx Mx Wx 2W . Условие прочности по теории наибольших касательных напряжений i 2 4 2 1 W M 2 M x2 , отсюда находим . M 2 M x2 W 2,882 22 6 10 21,91см3 , 3 160 10 D 3 32 21,91 6,07см Условие прочности по энергетической теории i 2 3 2 M 2 M x2 W 32 21,00 M 2 0,75 M x2 , отсюда находим 2,882 0,75 22 6 10 21,00см3 , 3 160 10 D 3 1 W 5,98см . Таким образом, по обеим теориям прочности получили близкие результаты. Примем D 6,1см и определим наибольшие нормальные и касательные напряжения для сечения совпадающего с заделкой. W 6,13 32 22,3см3 , Wx 2 W 44,6см3 ; M 2,88 103 max,min 129,1МПа ; W 22,3 106 Mx 2 103 44,8МПа W x 44,6 106 Определим угол наклона нейтральной линии к оси tg ( 0 ) Оz ( x M Mz y y z 0 ), Jz Jy Jz M y 2,4 1,5 , 0 56,30 Jy Mz 1,6 Рис.3.2 Эпюры касательных и нормальных напряжений