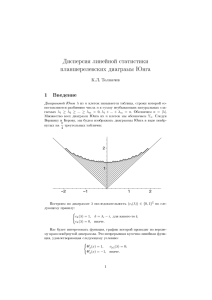
1 Условия задачи 2 Перевод уранения колебаний в полярные

1
2
Óñëîâèÿ çàäà÷è
Utt = a2 ∆U
(1)
U |r=r0 = 0
(2)
Ut |t=0 = 0
r2
U |t=0 = A 1 − 2
r0
(3)
(4)
Ïåðåâîä óðàíåíèÿ êîëåáàíèé â ïîëÿðíûå êîîðäèíàòû
U = U (t, r, ϕ)
∆U = Uxx + Uyy = Urr +
U (t, r, ϕ) = U (t, r, ϕ + 2π)
(5)
x = r cos ϕ
y = r sin ϕ
(6)
1
1
1 ∂
1
Uϕϕ + Ur =
(rUr ) + 2 Uϕϕ
r2
r
r ∂r
r
(7)
(ñì çàäà÷ó 60)
1
1
1
Utt = Urr + 2 Uϕϕ + Ur
2
a
r
r
3
(8)
Ðåøåíèå ðàçäåëåíèåì ïåðåìåííûõ
Ðåøàåì ðàçäåëåíèåì ïåðåìåííûõ óðàâíåíèå êîëåáàíèé ñ ãðàíè÷íûìè óñëîâèÿìè, íî áåç íà÷àëüíûõ.
U (t, r, ϕ) = T (t) R (r) Φ (ϕ)
(9)
Èç (5)
Φ (ϕ) = Φ (ϕ + 2π)
(10)
1
1
1
1
0
00
00
00
RΦT = ΦT R + 2 T RΦ + T ΦR ·
a2
r
r
T RΦ
(11)
1 T 00
R00
1 Φ00
1 R0
=
+ 2
+
=κ
2
a T
R
r Φ
r R
(12)
κt0 = 0,
3.1
κr0 = κϕ0 = 0,
=⇒
κ = const
(13)
Ïðîñòðàíñòâåííàÿ ÷àñòü
R00
1 Φ00
1 R0
+ 2
+
=κ
R
r Φ
r R
R00
R0
Φ00
r2
+r
− κr2 = −
=µ
R
R
Φ
µ = const
1
(14)
(15)
3.1.1
Óãëîâàÿ ÷àñòü
−
Φ00
=µ
Φ
(16)
Èç (16) ïðè óñëîâèè (10), êàê â çàäà÷å 60 ïîëó÷àåì
µ = n2
(17)
Φn = Cn1 cos (nϕ) + Cn2 sin (nϕ) ,
(18)
n = 0, 1, 2 . . ..
3.1.2
Ðàäèàëüíàÿ ÷àñòü
Ïîäñòàâèì (17) â (15):
r2
Çàìåíà
R0
R00
+r
− κr2 = n2
R
R
(19)
r2 R00 + rR0 − κr2 R − Rn2 = 0
(20)
n2
1
R00 + R0 − κR − 2 R = 0
r
r
(21)
√
−κ
ρ
√
dR √
d2 R
dR dρ
d dR √
d2 R dρ
=
= −κ 2
R0 =
−κ,
R00 =
−κ = −κ 2
dρ dr
dρ
dr dρ
dρ dr
dρ
√
√
2
d2 R
−κ dR √
−κ
−κ 2 +
−κ − κR − n2
R=0
dρ
ρ dρ
ρ
d2 R 1 dR
n2
+
+ 1− 2 R=0
dρ2
ρ dρ
ρ
√
−κr
R = C 3 Jn (ρ) = C 3 Jn
1
=
r
ρ
,
r= √
−κ
(22)
(23)
(24)
(25)
(26)
Èç (2) ñëåäóåò
(27)
R (r0 ) = 0
Jn
√
−κr0 = 0
=⇒
√
(n)
−κr0 = µk
=⇒
!
(n) 2
µk
κ=−
r0
(n) r
3
Rnk = Cnk
Jn µk
r0
2
√
(n)
−κ =
µk
,
r0
k∈N
(28)
(29)
(30)
3.2
Âðåìåííàÿ ÷àñòü
Ïîäñòàâèì (29) â (12)
!
(n) 2
µk
r0
!2
(n)
µk a
T
r0
!
1 T 00
=−
a2 T
(31)
T 00 = −
(32)
(n)
4
Tnk = Cnk
cos
Îáùåå ðåøåíèå òàêîå:
U=
µk a
t
r0
∞ X
∞
X
5
+ Cnk
sin
(n)
µk a
t
r0
!
(33)
Tnk Rnk Φn =
n=0 k=1
=
∞ X
∞
X
"
(n)
µk a
t
r0
4
Cnk
cos
n=0 k=1
4
4.1
!
5
+ Cnk
sin
!#
(n)
1
µk a
(n) r
3
t
Cn cos (nϕ) + Cn2 sin (nϕ)
Cnk Jn µk
r0
r0
(34)
Íà÷àëüíûå óñëîâèÿ
Íà÷àëüíàÿ ñêîðîñòü
Ut |t=0 = 0
5
Cnk
= 0.
=⇒
(35)
Äîêàçàòåëüñòâî. Âîñïîëüçóåìñÿ òåì, ÷òî
ˆπ
−π
ˆπ

n 6= m
 0,
π, n = m 6= 0
cos (mϕ) cos (nϕ) dϕ =

2π, n = m = 0
−π

n 6= m
 0,
π, n = m 6= 0
sin (mϕ) sin (nϕ) dϕ =

0, n = m = 0
ˆπ
sin (mϕ) cos (nϕ) dϕ = 0
(36)
∞ ∞ "
#
(n)
X X
1
(n) r
5 µk a
3
Cnk
Cnk
Jn µk
Cn cos (nϕ) + Cn2 sin (nϕ) = 0
dϕ cos (mϕ) · r0
r0
(37)
−π
ˆπ
−π
n=0 k=1
Òåïåðü âîñïîëüçóåìñÿ îðòîãîíàëüíîñòüþ ôóíêöèé Áåññåëÿ:
ˆr0
r2 h 0 (m) i2
(m) r
(m) r
Jm µk
rdr = δkn 0 Jm
µn
.
Jm µn
r0
r0
2
(38)
0
Äîìíîæèì è ïðîèíòåãðèðóåì:
ˆr0
0
∞
(m)
X
(m) r
(m) r
5 µk a 3
1
dr rJm µn
· Kπ
Cmk
Cmk Jm µk
Cm
=0,
r0
r0
r0
k=1
3
K = 1, 2;
m = 0, 1, . . .
(39)
5
Cmn
(m)
i2
2 h
µn a 3
1 r0
0
Jm
Cmn Cm
µ(m)
= 0,
n
r0
2
(40)
5
1
Cmn
Cm
= 0.
"
#
ˆπ
∞ X
∞
(n)
X
1
(n) r
5 µk a
3
dϕ sin (mϕ) · Cnk
Cnk Jn µk
Cn cos (nϕ) + Cn2 sin (nϕ) = 0
r0
r0
(42)
n=0 k=1
−π
ˆr0
0
(41)
X
∞
(m)
(m) r
(m) r
5 µk a 3
2
dr rJm µn
· π
Cmk
Cmk Jm µk
Cm
=0,
r0
r0
r0
m = 1, 2, . . .
(43)
k=1
5
Cmn
(m)
i2
2 h
µn a 3
0
2 r0
µ(m)
Jm
= 0,
Cmn Cm
n
r0
2
(44)
5
2
Cmn
Cm
= 0.
(45)
Ïîäñòàâèì â (34):
U=
∞
∞ X
X
!
(n)
4 3 1
µk a
(n) r
4
3
t Jn µk
Cnk Cnk Cn cos (nϕ) + Cnk
Cnk
Cn2 sin (nϕ) =
r0
r0
cos
n=0 k=1
îáîçíà÷èì
7
6
4
3
4
3
, Cnk
Cnk
Cn2 ≡ Cnk
Cnk
Cnk
Cn1 ≡ Cnk
=
∞
∞ X
X
cos
n=0 k=1
4.2
!
(n)
6
µk a
(n) r
7
t Jn µk
Cnk cos (nϕ) + Cnk
sin (nϕ) .
r0
r0
Íà÷àëüíîå îòêëîíåíèå
r2
U |t=0 = A 1 −
r0
∞ X
∞
X
(48)
ˆπ
ˆπ
6
r2
(n) r
7
Jn µk
Cnk cos (nϕ) + Cnk
sin (nϕ) sin (mϕ) dϕ = A 1 − 2
sin (mϕ) dϕ
r0
r0
(49)
Ñìåðòü óãëîâîé ÷àñòè
sin:
∞ X
∞
X
n=0 k=1
−π
∞ X
∞
X
−π
(n)
Jn µk
n=0 k=1
m 6= 0
(47)
6
r2
(n) r
7
Cnk cos (nϕ) + Cnk
sin (nϕ) = A 1 − 2
Jn µk
r0
r0
n=0 k=1
4.2.1
(46)
ˆr0
0
r
r0
ˆπ
7
Cnk
sin (nϕ) sin (mϕ) dϕ = A 1 −
−π
ˆπ
2
r
r02
sin (mϕ) dϕ
−π
X
∞
(m) r
(m) r
7
dr rJm µn
·
Jm µk
Cmk
π = 0,
r0
r0
k=1
4
(50)
(51)
7
Cmn
r02 h 0 (m) i2
= 0,
Jm µn
2
(52)
7
Cmn
= 0.
(53)
Ïîäñòàâèì â (46) è ïîëó÷èì íîâûé âèä ðåøåíèÿ:
U=
∞ X
∞
X
(n)
cos
n=0 k=1
µk a
t
r0
!
(n) r
6
Jn µk
Cnk
cos (nϕ) .
r0
(54)
r2
cos (nϕ) = A 1 − 2
r0
(55)
Íà÷àëüíîå óñëîâèå (4) ïðåâðàòèòñÿ â
∞ X
∞
X
Jn
(n)
µk
n=0 k=1
cos:
∞ X
∞
X
n=0 k=1
r
r0
6
Cnk
.
ˆπ
ˆπ
r2
(n) r
6
Cnk
cos (nϕ) cos (mϕ) dϕ = A 1 − 2
cos (mϕ) dϕ
Jn µk
r0
r0
−π
m 6= 0
ˆr0
(56)
−π
X
∞
(m) r
6
(m) r
dr rJm µn
·
Jm µk
Cmk
π=0
r0
r0
(57)
k=1
0
6
Cmn
r02 h 0 (m) i2
Jm µn
=0
2
6
Cmn
= 0,
(58)
(59)
m = 1, 2, . . .
è (54) ïðåâðàòèòñÿ â
U=
∞ X
∞
X
(n)
µk a
t
r0
cos
n=0 k=1
4.2.2
!
Jn
(n)
µk
r
r0
6
Cnk
m = 0:
∞
X
k=1
ˆr0
dr rJ0
k=1
ˆr0
6
C0k
J0
µ(0)
n
cos
µk a
t
r0
!
(0) r
6
Jn µk
C0k
.
r0
r
µ(0)
n
r0
r
r0
X
∞
r2
(0) r
6
·
J0 µk
C0k = A 1 − 2 ,
r0
r0
(61)
(62)
k=1
J0
(60)
6
C0k
r2
(0) r
6
J0 µk
C0k 2π = A 1 − 2 2π,
r0
r0
0
∞
X
(0)
k=1
Íàõîæäåíèå îñòàâøèõñÿ êîýôôèöèåíòîâ
Òåïåðü ïóñòü â (56)
cos (nϕ) =
∞
X
(0)
µk
r
r0
ˆr0 1−
rdr = A
0
0
5
r2
r02
r
J0 µ(0)
rdr.
n
r0
(63)
Äàëåå áóäóò àêòèâíî èñïîëüçîâàòüñÿ ôîðìóëû
ν
Jν − Jν0 = Jν+1 ,
x
ν
Jν + Jν0 = Jν−1 .
x
Ëåâàÿ ÷àñòü (63):
∞
X
ˆr0
6
C0k
k=1
J0
µ(0)
n
r
r0
J0
(0)
µk
r
r0
rdr =
J00 = −J1
6
= C0n
A
è ñ çàìåíîé
µ(0)
n
0
ñ ó÷¼òîì
J0 (ρ) =
(ρ) +
J10
r0
(0)
µn
(64)
r0
r=
ρ:
(0)
µn

!2 ˆ
µ(0)
n
r0
1 −
(0)
µn
ρ
!2 
 J0 (ρ) ρdρ =
(0)
µn
0
(ρ):


!2 ˆ
µ(0)
n
2
ρ
r0

 1
0
1
−
J
(ρ)
+
J
(ρ)
ρdρ =

2 
1
1
(0)
ρ
(0)
µn
µ
n
0
=
=
i2
2 h
r02 h 0 (0) i2
6 r0
J0 µn
= C0n
J00 µ(0)
=
n
2
2
r02 h (0) i2
J 1 µn
.
2
r
= ρ;
r0
ˆr0 r2
r
1 − 2 J0 µ(0)
rdr =
n
r0
r0
1
ρ J1
6
C0k
δnk
k=1
0
Ïðàâàÿ ÷àñòü(63) áåç
∞
X
!2



(0)
µn
ˆ


0


(0)
2
ρ


1 − 2  J1 (ρ) dρ +
(0)
µn
µn
ˆ
0

3
ρ
 0


ρ − 2  J1 (ρ) dρ =
(0)
µn

µ(0)






n
!2 ˆ
µ(0)
µ(0)
n
n
ˆ


ρ2 
3ρ2 
r0
ρ3 




−
1 − 1 − 2  J1 (ρ) dρ + ρ − 2  J 1 (ρ)
2  J 1 (ρ) dρ

=
(0)
(0)
(0)
(0)
µn
µ
µ
µ
n
n
n
0
0

=
0





!2 ˆ
µ(0)
µ(0)
n
n
ˆ
2
2
r0
3ρ 
ρ






1 − 1 − 2  J1 (ρ) dρ −
2  J 1 (ρ) dρ =
(0)
(0)
(0)
µn
µn
µn
0
0

=
(0)
=
µn
ˆ
r02
(0)
µn
2
0
(0)
2ρ2
2r02
2 J1 (ρ) dρ = 4
(0)
(0)
µn
µn
6
µn
ˆ
ρ2 J1 (ρ) dρ.
0
(65)
Âû÷èñëèì îòäåëüíî èíòåãðàë. Åù¼ ðàç ïî ÷àñòÿì,
(0)
J1 = −J00 :
(0)
µn
ˆ
µn
ˆ
2
ρ J1 (ρ) dρ = −
0
(0)
µ(0)
ρ2 J00 (ρ) dρ = − ρ2 J 0 (ρ)0 n +
0
µn
ˆ
2ρJ 0 (ρ) dρ = 2
0
(0)
ρ
1
0
J1 (ρ) + J1 (ρ) dρ =
ρ
0
(0)
µn
ˆ
=2
(0)
µn
ˆ
µn
ˆ
ρJ10 (ρ) dρ =
J1 (ρ) dρ + 2
0
(66)
0
È åù¼ ðàç:
(0)
(0)
µn
ˆ
=2
µ(0)
ρJ 1 (ρ)|0 n
J1 (ρ) dρ + 2
µn
ˆ
−2
0
(0)
J 1 (ρ) dρ = 2µ(0)
.
n J 1 µn
0
Èòàê,
(0)
µn
ˆ
(0)
ρ2 J1 (ρ) dρ = 2µ(0)
,
n J 1 µn
(67)
0
(0)
µn
ˆ
ˆr0 2
2r
4r2
r
r2
,
rdr = 04
ρ2 J1 (ρ) dρ = 03 J 1 µ(0)
1 − 2 J0 µ(0)
n
n
r0
r0
(0)
(0)
µn
µn
0
0
(68)
è (63) çàïèñûâàåòñÿ â âèäå
6
C0n
r02 h (0) i2
4r2
J 1 µn
= A 03 J 1 µ(0)
,
n
2
(0)
µn
(69)
îòêóäà
6
C0n
=
8A
8A
(0)
J
µ
3 h 3 i2 1 n = ,
(0)
(0)
(0)
(0)
µn
J 1 µn
µn
J 1 µn
(70)
÷òî ïîäñòàâëÿåòñÿ â (60), è íàõîäèòñÿ îêîí÷àòåëüíûé îòâåò:
U=
∞
X
k=1
(0)
cos
!
µk a
t
r0
(0)
Jn µk
r
r0
6
C0k
(0) µk a
cos
∞
r0 t
X
(0) r
= 8A
.
3 Jn µk
r0
(0)
(0)
k=1 µn
J 1 µn
7
(71)