ЭФФЕКТИВНОЕ ОБСЛУЖИВАНИЕ СЕТИ АВТОДОРОГ РЕГИОНА

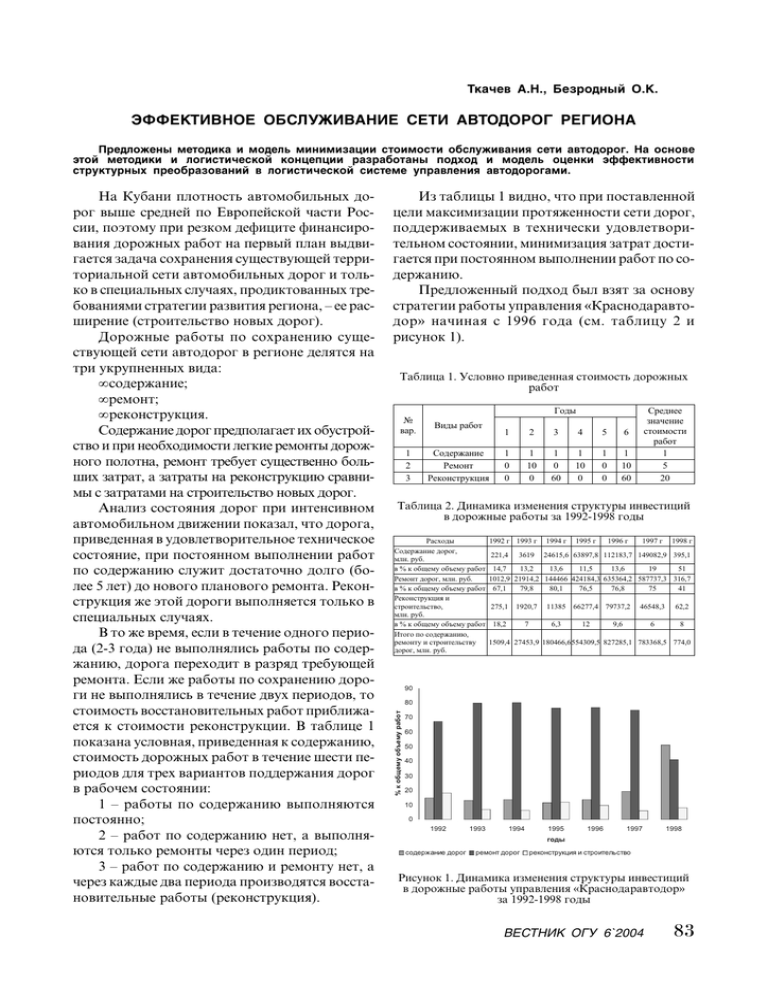
Òêà÷åâ À.Í., Áåçðîäíûé Î.Ê.
ÝÔÔÅÊÒÈÂÍÎÅ ÎÁÑËÓÆÈÂÀÍÈÅ ÑÅÒÈ ÀÂÒÎÄÎÐÎÃ ÐÅÃÈÎÍÀ
Ïðåäëîæåíû ìåòîäèêà è ìîäåëü ìèíèìèçàöèè ñòîèìîñòè îáñëóæèâàíèÿ ñåòè àâòîäîðîã. Íà îñíîâå
ýòîé ìåòîäèêè è ëîãèñòè÷åñêîé êîíöåïöèè ðàçðàáîòàíû ïîäõîä è ìîäåëü îöåíêè ýôôåêòèâíîñòè
ñòðóêòóðíûõ ïðåîáðàçîâàíèé â ëîãèñòè÷åñêîé ñèñòåìå óïðàâëåíèÿ àâòîäîðîãàìè.
Èç òàáëèöû 1 âèäíî, ÷òî ïðè ïîñòàâëåííîé
öåëè ìàêñèìèçàöèè ïðîòÿæåííîñòè ñåòè äîðîã,
ïîääåðæèâàåìûõ â òåõíè÷åñêè óäîâëåòâîðèòåëüíîì ñîñòîÿíèè, ìèíèìèçàöèÿ çàòðàò äîñòèãàåòñÿ ïðè ïîñòîÿííîì âûïîëíåíèè ðàáîò ïî ñîäåðæàíèþ.
Ïðåäëîæåííûé ïîäõîä áûë âçÿò çà îñíîâó
ñòðàòåãèè ðàáîòû óïðàâëåíèÿ «Êðàñíîäàðàâòîäîð» íà÷èíàÿ ñ 1996 ãîäà (ñì. òàáëèöó 2 è
ðèñóíîê 1).
Òàáëèöà 1. Óñëîâíî ïðèâåäåííàÿ ñòîèìîñòü äîðîæíûõ
ðàáîò
Ñðåäíåå
çíà÷åíèå
ñòîèìîñòè
ðàáîò
1
5
20
Ãîäû
¹
âàð.
Âèäû ðàáîò
1
2
3
Ñîäåðæàíèå
Ðåìîíò
Ðåêîíñòðóêöèÿ
1
2
3
4
5
6
1
0
0
1
10
0
1
0
60
1
10
0
1
0
0
1
10
60
Òàáëèöà 2. Äèíàìèêà èçìåíåíèÿ ñòðóêòóðû èíâåñòèöèé
â äîðîæíûå ðàáîòû çà 1992-1998 ãîäû
Ðàñõîäû
Ñîäåðæàíèå äîðîã,
ìëí. ðóá.
â % ê îáùåìó îáúåìó ðàáîò
Ðåìîíò äîðîã, ìëí. ðóá.
â % ê îáùåìó îáúåìó ðàáîò
Ðåêîíñòðóêöèÿ è
ñòðîèòåëüñòâî,
ìëí. ðóá.
â % ê îáùåìó îáúåìó ðàáîò
Èòîãî ïî ñîäåðæàíèþ,
ðåìîíòó è ñòðîèòåëüñòâó
äîðîã, ìëí. ðóá.
1992 ã 1993 ã
1994 ã
221,4
24615,6 63897,8 112183,7 149082,9 395,1
3619
1995 ã
1996 ã
1997 ã
1998 ã
14,7
13,2
13,6
11,5
13,6
19
51
1012,9 21914,2 144466 424184,3 635364,2 587737,3 316,7
67,1
79,8
80,1
76,5
76,8
75
41
275,1
1920,7
18,2
7
11385 66277,4 79737,2
6,3
12
46548,3
62,2
6
8
9,6
1509,4 27453,9 180466,6554309,5 827285,1 783368,5 774,0
90
80
% ê îáùåìó îáúåìó ðàáîò
Íà Êóáàíè ïëîòíîñòü àâòîìîáèëüíûõ äîðîã âûøå ñðåäíåé ïî Åâðîïåéñêîé ÷àñòè Ðîññèè, ïîýòîìó ïðè ðåçêîì äåôèöèòå ôèíàíñèðîâàíèÿ äîðîæíûõ ðàáîò íà ïåðâûé ïëàí âûäâèãàåòñÿ çàäà÷à ñîõðàíåíèÿ ñóùåñòâóþùåé òåððèòîðèàëüíîé ñåòè àâòîìîáèëüíûõ äîðîã è òîëüêî â ñïåöèàëüíûõ ñëó÷àÿõ, ïðîäèêòîâàííûõ òðåáîâàíèÿìè ñòðàòåãèè ðàçâèòèÿ ðåãèîíà, – åå ðàñøèðåíèå (ñòðîèòåëüñòâî íîâûõ äîðîã).
Äîðîæíûå ðàáîòû ïî ñîõðàíåíèþ ñóùåñòâóþùåé ñåòè àâòîäîðîã â ðåãèîíå äåëÿòñÿ íà
òðè óêðóïíåííûõ âèäà:
• ñîäåðæàíèå;
• ðåìîíò;
• ðåêîíñòðóêöèÿ.
Ñîäåðæàíèå äîðîã ïðåäïîëàãàåò èõ îáóñòðîéñòâî è ïðè íåîáõîäèìîñòè ëåãêèå ðåìîíòû äîðîæíîãî ïîëîòíà, ðåìîíò òðåáóåò ñóùåñòâåííî áîëüøèõ çàòðàò, à çàòðàòû íà ðåêîíñòðóêöèþ ñðàâíèìû ñ çàòðàòàìè íà ñòðîèòåëüñòâî íîâûõ äîðîã.
Àíàëèç ñîñòîÿíèÿ äîðîã ïðè èíòåíñèâíîì
àâòîìîáèëüíîì äâèæåíèè ïîêàçàë, ÷òî äîðîãà,
ïðèâåäåííàÿ â óäîâëåòâîðèòåëüíîå òåõíè÷åñêîå
ñîñòîÿíèå, ïðè ïîñòîÿííîì âûïîëíåíèè ðàáîò
ïî ñîäåðæàíèþ ñëóæèò äîñòàòî÷íî äîëãî (áîëåå 5 ëåò) äî íîâîãî ïëàíîâîãî ðåìîíòà. Ðåêîíñòðóêöèÿ æå ýòîé äîðîãè âûïîëíÿåòñÿ òîëüêî â
ñïåöèàëüíûõ ñëó÷àÿõ.
 òî æå âðåìÿ, åñëè â òå÷åíèå îäíîãî ïåðèîäà (2-3 ãîäà) íå âûïîëíÿëèñü ðàáîòû ïî ñîäåðæàíèþ, äîðîãà ïåðåõîäèò â ðàçðÿä òðåáóþùåé
ðåìîíòà. Åñëè æå ðàáîòû ïî ñîõðàíåíèþ äîðîãè íå âûïîëíÿëèñü â òå÷åíèå äâóõ ïåðèîäîâ, òî
ñòîèìîñòü âîññòàíîâèòåëüíûõ ðàáîò ïðèáëèæàåòñÿ ê ñòîèìîñòè ðåêîíñòðóêöèè. Â òàáëèöå 1
ïîêàçàíà óñëîâíàÿ, ïðèâåäåííàÿ ê ñîäåðæàíèþ,
ñòîèìîñòü äîðîæíûõ ðàáîò â òå÷åíèå øåñòè ïåðèîäîâ äëÿ òðåõ âàðèàíòîâ ïîääåðæàíèÿ äîðîã
â ðàáî÷åì ñîñòîÿíèè:
1 – ðàáîòû ïî ñîäåðæàíèþ âûïîëíÿþòñÿ
ïîñòîÿííî;
2 – ðàáîò ïî ñîäåðæàíèþ íåò, à âûïîëíÿþòñÿ òîëüêî ðåìîíòû ÷åðåç îäèí ïåðèîä;
3 – ðàáîò ïî ñîäåðæàíèþ è ðåìîíòó íåò, à
÷åðåç êàæäûå äâà ïåðèîäà ïðîèçâîäÿòñÿ âîññòàíîâèòåëüíûå ðàáîòû (ðåêîíñòðóêöèÿ).
70
60
50
40
30
20
10
0
1992
1993
1994
1995
1996
1997
1998
ãîäû
ñîäåðæàíèå äîðîã
ðåìîíò äîðîã
ðåêîíñòðóêöèÿ è ñòðîèòåëüñòâî
Ðèñóíîê 1. Äèíàìèêà èçìåíåíèÿ ñòðóêòóðû èíâåñòèöèé
â äîðîæíûå ðàáîòû óïðàâëåíèÿ «Êðàñíîäàðàâòîäîð»
çà 1992-1998 ãîäû
ÂÅÑÒÍÈÊ ÎÃÓ 6`2004
83
Ýêîíîìè÷åñêèå íàóêè
Ïðèâåäåííûå ðàññóæäåíèÿ ïîçâîëÿþò íà
êà÷åñòâåííîì óðîâíå îïðåäåëèòü ïðèîðèòåòíîñòü äîðîæíûõ ðàáîò, íî äëÿ êîëè÷åñòâåííîé
îïòèìèçàöèè èõ íåäîñòàòî÷íî.
Ìîäåëü ìèíèìèçàöèè ñòîèìîñòè
îáñëóæèâàíèÿ ñåòè àâòîäîðîã
Äëÿ êîëè÷åñòâåííîé îïòèìèçàöèè ðàñïðåäåëåíèÿ ãîäîâûõ îáúåìîâ èíâåñòèöèé ïî âèäàì
äîðîæíûõ ðàáîò, ïðîâåäåíèÿ èìèòàöèîííûõ
ýêñïåðèìåíòîâ è ñîçäàíèÿ ïîðòôåëÿ èíâåñòèöèîííûõ ïðîåêòîâ áûëà ðàçðàáîòàíà ëèíåéíî-äèíàìè÷åñêàÿ ìîäåëü ðåøåíèÿ óêàçàííîé çàäà÷è.
Ìîäåëü ðàçðàáîòàíà äëÿ ó÷àñòêà ñåòè äîðîã, íàõîäÿùåãîñÿ ê ïåðâîìó ïåðèîäó ïëàíèðîâàíèÿ â èñïðàâíîì ñîñòîÿíèè. Êðèòåðèåì îïòèìèçàöèè ìîäåëè ÿâëÿåòñÿ ìàêñèìóì ïðîòÿæåííîñòè äîðîã ó÷àñòêà, ñîäåðæàùèõñÿ â òåõíè÷åñêè óäîâëåòâîðèòåëüíîì ñîñòîÿíèè ïî
îêîí÷àíèè ñðîêà ïëàíèðîâàíèÿ. Îíà ôîðìóëèðóåòñÿ ñëåäóþùèì îáðàçîì.
Ìàêñèìèçèðîâàòü ñóììàðíóþ ïðîòÿæåííîñòü äîðîã ó÷àñòêà ñåòè ñ âûïîëíåííûìè äîðîæíûìè ðàáîòàìè çà çàäàííûé ïåðèîä ïëàíèðîâàíèÿ èíâåñòèöèé
m
Z = ∑ Si → max
i =1
ïðè óñëîâèÿõ:
1) ïî îáúåìàì èíâåñòèöèé:
m
∑ a ijx ij = b j; j = 1, n ;
i =1
2) ïî ïðîòÿæåííîñòè äîðîã ó÷àñòêà ñåòè:
j− i
m −1
k =1
i =1
− ∑ x mk +
∑ x ij ≤ S; j = 1, n ;
3) ïî ïðåäåëüíîé ïðîòÿæåííîñòè äîðîã ïî
âèäàì ðàáîò:
j−1
− ∑ x mk + x ij ≤ S; i = 1, m − 1 ; j = 1, n ;
k =1
4) ïî ñóììàðíîé ïðîòÿæåííîñòè äîðîã ïî
âèäàì ðàáîò:
n
n – ìíîæåñòâî ïåðèîäîâ ïëàíèðîâàíèÿ èíâåñòèöèé;
bj – îáúåì èíâåñòèöèé â äîðîæíûå ðàáîòû â
n ïåðèîäå;
S – ïðîòÿæåííîñòü äîðîã ó÷àñòêà ñåòè ê íà÷àëó 1-ãî ïåðèîäà ïëàíèðîâàíèÿ;
aij – çàòðàòû íà 1 êì i-ãî âèäà ðàáîòû â j-ì
ïåðèîäå;
xij – ïðîòÿæåííîñòü äîðîã äëÿ âûïîëíåíèÿ
i-ãî âèäà ðàáîò â j-ì ïåðèîäå;
xmk – ïðîòÿæåííîñòü ïîñòðîåííûõ äîðîã â
k-ì ïåðèîäå;
Si – ñóììàðíàÿ ïðîòÿæåííîñòü äîðîã äëÿ
âûïîëíåíèÿ i-ãî âèäà ðàáîò çà âåñü ïåðèîä
ïëàíèðîâàíèÿ.
Ðåçóëüòàòû ðàñ÷åòîâ ïî ðàçðàáîòàííîé ìîäåëè ïðèìåíÿþòñÿ â Êðàñíîäàðñêîì êðàå ïðè
ïðîãíîçèðîâàíèè îáúåìîâ è âèäîâ äîðîæíûõ
ðàáîò ñ 1996 ãîäà.
Ìîäåëü îöåíêè ýôôåêòèâíîñòè
ñòðóêòóðíûõ ïðåîáðàçîâàíèé
Ñðàâíèòåëüíûé àíàëèç ëîãèñòè÷åñêèõ ñèñòåì óïðàâëåíèÿ àâòîäîðîãàìè ðåãèîíà â äîðåôîðìåííûé è ïîñëåðåôîðìåííûé ïåðèîäû ïîçâîëÿåò îöåíèòü ýôôåêòèâíîñòü ïðîâåäåííûõ
ñòðóêòóðíûõ ïðåîáðàçîâàíèé.
Äî íà÷àëà ðåôîðì ëîãèñòè÷åñêàÿ ñèñòåìà
óïðàâëåíèÿ àâòîäîðîãàìè èìåëà âèä, èçîáðàæåííûé íà ðèñ. 2.
Êàê âèäíî èç ýòîãî ðèñóíêà, ñðåäñòâà äîðîæíîãî ôîíäà â ðàçìåðå Ää= (1-kó)Äô, ãäå kó –
äîëÿ, èäóùàÿ íà êîìïåíñàöèþ èçäåðæåê óïðàâëåíèÿ, ðàçäåëÿåòñÿ íà äâå ñîñòàâëÿþùèå:
Äð – äëÿ îïëàòû äîðîæíûõ ðàáîò; Äë– äëÿ îïëàòû ìàòåðèàëüíî-òåõíè÷åñêîãî îáåñïå÷åíèÿ
äîðîæíûõ ðàáîò.
 ðåçóëüòàòå äåíåæíûå ïîòîêè ïðèîáðåòàþò ìàòåðèàëüíîå âîïëîùåíèå â ïîòîêàõ Ìð è
Ì0, ïðåîáðàçóÿñü â ïðîöåññå äîðîæíûõ ðàáîò
ÄÐ â êèëîìåòðû îáñëóæåííûõ ó÷àñòêîâ äîðîã.
− S i + ∑ x ij = 0; i = 1, m ;
j=1
5) ïî èñêëþ÷åíèþ âèäîâ ðàáîò â 1-ì è 2-ì
ïåðèîäàõ ïëàíèðîâàíèÿ èíâåñòèöèé:
x ( j+1) j = 0 ïðè j = 1 ;
x ( j+ 2) j = 0 ïðè j = 1 ;
x ( j+1) j = 0 ïðè j = 2 ;
6) ïî íåîòðèöàòåëüíîñòè ïåðåìåííûõ:
x ij ≥ 0; i = 1, m ; j = 1, n ,
ãäå i – íîìåð âèäà äîðîæíîé ðàáîòû, i ∈ m;
j – íîìåð ãîäà ôèíàíñèðîâàíèÿ, j ∈ n;
m – ìíîæåñòâî âèäîâ ðàáîò;
84
ÂÅÑÒÍÈÊ ÎÃÓ 6`2004
Ðèñóíîê 2. Ëîãèñòè÷åñêàÿ ñèñòåìà óïðàâëåíèÿ
àâòîäîðîãàìè äî íà÷àëà ðåôîðì
Òêà÷åâ À.Í., Áåçðîäíûé Î.Ê.
Ýôôåêòèâíîå îáñëóæèâàíèå ñåòè àâòîäîðîã ðåãèîíà
 ñèñòåìå ðèñ. 2 âûõîäíîé ìàòåðèàëüíûé
ïîòîê Ìäîð îïðåäåëÿåòñÿ ñóììîé ïîòîêîâ òðóäà
è òåõíè÷åñêèõ ñðåäñòâ Ìð è ìàòåðèàëüíî-òåõíè÷åñêîãî ñíàáæåíèÿ Ì0:
Ìäîð = k(Ìð +Ì0 ),
ãäå k – êîýôôèöèåíò ïðåîáðàçîâàíèÿ òðóäî-ìàòåðèàëüíûõ çàòðàò â ïðîöåññå äîðîæíûõ ðàáîò
â äîðîãè.
Ðàáîòû ïî îáñëóæèâàíèþ äîðîã äåëÿòñÿ íà
òðè âèäà: ñîäåðæàíèå, ðåìîíò è ðåêîíñòðóêöèÿ.
Ñåáåñòîèìîñòü 1 êì ýòèõ ðàáîò ðàçëè÷íà. Ì äîð
ïðåäñòàâëÿåò ñîáîé ñóììó ïðîòÿæåííîñòåé äîðîæíûõ ó÷àñòêîâ, íà êîòîðûõ âûïîëíåíû ïåðå÷èñëåííûå ðàáîòû, ò. å.:
Ìäîð = Ìñ+ Ìð +Ìðåê,
ãäå Ìñ – ïðîòÿæåííîñòü äîðîæíûõ ó÷àñòêîâ, íà
êîòîðûõ âûïîëíåíû ðàáîòû ïî ñîäåðæàíèþ; Ìð
– ïðîòÿæåííîñòü äîðîæíûõ ó÷àñòêîâ, íà êîòîðûõ âûïîëíåíû ðàáîòû ïî ðåìîíòó; Ìðåê – ïðîòÿæåííîñòü äîðîæíûõ ó÷àñòêîâ, íà êîòîðûõ
âûïîëíåíû ðàáîòû ïî ðåêîíñòðóêöèè.
Îòíîøåíèå ðåàëüíîé ïðîòÿæåííîñòè ó÷àñòêîâ ê ïðîòÿæåííîñòè, ïðèâåäåííîé ê ðàáîòàì
ïî ñîäåðæàíèþ (ñàìûì äåøåâûì), íàçîâåì êîýôôèöèåíòîì ýôôåêòèâíîñòè óïðàâëåíèÿ äîðîæíûìè ðàáîòàìè kýô, êîòîðûé îïðåäåëÿåòñÿ
ñîîòíîøåíèåì âûïîëíåííûõ ðàáîò:
k ýô =
Ì äîð
Ì äîð
.
Òîãäà ðåàëüíàÿ ñóììàðíàÿ ïðîòÿæåííîñòü
äîðîæíûõ ó÷àñòêîâ, íà êîòîðûõ âûïîëíåíû
îáñëóæèâàþùèå ðàáîòû,
Ì äîð = k ýô
èëè
Ää
Ññ
Ì äîð = k ýô (1 - k ó )
Äô
Ññ
,
(1)
ãäå Ññ – ñòîèìîñòü ðàáîò ïî ñîäåðæàíèþ 1 êì
äîðîã.
Èíûìè ñëîâàìè, ïðîòÿæåííîñòü îáñëóæåííûõ ó÷àñòêîâ äîðîã ïðîïîðöèîíàëüíà îáúåìó
ñðåäñòâ èç äîðîæíîãî ôîíäà è êîýôôèöèåíòó
óïðàâëåíèÿ.
 ðåçóëüòàòå ïðîâåäåííîé ñòðóêòóðèçàöèè
ëîãèñòè÷åñêàÿ ñèñòåìà óïðàâëåíèÿ àâòîäîðîãàìè
ðåãèîíà ïðèîáðåëà âèä, ïîêàçàííûé íà ðèñ. 3.
 ñîñòàâ ñèñòåìû ââåäåíà ïîäñèñòåìà ðàñïðåäåëåíèÿ èíâåñòèöèé (ï/ñ ÐÈ), áëàãîäàðÿ êîòîðîé ñðåäñòâà äîðîæíîãî ôîíäà Äô çà âû÷åòîì ÷àñòè kóÄô, èäóùåé íà ðàñõîäû ïî óïðàâëåíèþ, ïîñòóïàþò íà îïëàòó ïðîåêòîâ, âûèãðàí-
Ðèñóíîê 3. Ëîãèñòè÷åñêàÿ ñèñòåìà óïðàâëåíèÿ
àâòîäîðîãàìè â ïîñëåðåôîðìåííûé ïåðèîä
íûõ ïîáåäèòåëÿìè òîðãîâ. Ñìûñë òîðãîâ â òîì,
÷òîáû ïîíèçèòü ñòîèìîñòü ïðîåêòîâ, à ðàçíîñòü
ìåæäó èõ íà÷àëüíîé è îêîí÷àòåëüíîé ñòîèìîñòüþ ÿâëÿåòñÿ ïðèáûëüþ ñèñòåìû óïðàâëåíèÿ.
Ïðèáûëü Äï íàïðàâëÿåòñÿ íà îïëàòó äîïîëíèòåëüíûõ äîðîæíûõ ðàáîò Äïä è èõ ìàòåðèàëüíîãî îáåñïå÷åíèÿ Äïñ.
Ýôôåêòèâíîñòü ïîäñèñòåìû ÐÈ îïðåäåëÿåòñÿ ïîëó÷àåìîé ïðèáûëüþ:
k ýò =
Ä ò − (Ä′ä + Ä ñ )
,
Äò
ãäå Ä 'Ä – îêîí÷àòåëüíàÿ ñòîèìîñòü ïðîåêòîâ
äîðîæíûõ ðàáîò; Äñ – îêîí÷àòåëüíàÿ ñòîèìîñòü
ïðîåêòîâ ìàòåðèàëüíî-òåõíè÷åñêîãî ñíàáæåíèÿ; Äò= (1-kó)Äô – ñðåäñòâà, íàïðàâëåííûå íà
òîðãè.
Ïðîâåäÿ àíàëèç ëîãèñòè÷åñêîé ñèñòåìû óïðàâëåíèÿ àâòîäîðîãàìè â ïîñëåðåôîðìåííûé
ïåðèîä (ðèñ. 3), àíàëîãè÷íûé äëÿ ýòîé ñèñòåìû
äî íà÷àëà ðåñòðóêòóðèçàöèè, ïîëó÷èì äëÿ âûõîäíîãî ìàòåðèàëüíîãî ïîòîêà:
Ì ′äîð = k ′ýô (1 - k ′ó )(1 + k ýò )
Ä ′ô
Ñ ′ñ
.
(2)
Îòëè÷èå (2) îò (1) ñîñòîèò â íàëè÷èè ñîìíîæèòåëÿ (1 + k ýò ) ≥ 1 , ó÷èòûâàþùåãî ïðèáûëü,
ïðèíîñèìóþ ïîäñèñòåìîé ðàñïðåäåëåíèÿ èíâåñòèöèé.
Ýôôåêòèâíîñòü Ý ðåñòðóêòóðèðîâàííîé ñèñòåìû ïî îòíîøåíèþ ê ñóùåñòâîâàâøåé ìîæåò
áûòü çàïèñàíà â âèäå:
Ý=
Ì ′äîð
Ì äîð .
Åñëè ïðåäïîëîæèòü ðàâíûå óñëîâèÿ, ò. å.
Ä ô' = Ä ô è Ñ 'ñ = Ñ ñ , à k’ó è kó << 1, òî
ÂÅÑÒÍÈÊ ÎÃÓ 6`2004
85
Ýêîíîìè÷åñêèå íàóêè
Ý=
k ′ýô
k ýô
Êîýôôèöèåíòû ýôôåêòèâíîñòè óïðàâëåíèÿ
k’ýô è kýô â ñðàâíèâàåìûõ ñèñòåìàõ ñóùåñòâåííî
îòëè÷àþòñÿ. Äåëî â òîì, ÷òî â ñóùåñòâîâàâøåé
ñèñòåìå öåëüþ ÄÐÑÏ ÿâëÿëîñü ïîâûøåíèå êàòåãîðèéíîñòè ðàáîò, à êàòåãîðèéíîñòü áûëà òåì
âûøå, ÷åì áîëüøå óäåëüíûé âåñ ðàáîò ïî ðåêîíñòðóêöèè äîðîã. Ïîýòîìó ïðè áîëüøèõ îáúåìàõ
ðàáîò â äåíåæíîì âûðàæåíèè ïðîòÿæåííîñòü
îáñëóæåííûõ äîðîæíûõ ó÷àñòêîâ áûëà ìåíüøå,
à çàðïëàòà áîëüøå (âûøå êàòåãîðèÿ – âûøå çàðïëàòà).
 ðåñòðóêòóðèðîâàííîé ñèñòåìå öåëüþ äåÿòåëüíîñòè ÄÐÑÏ ÿâëÿåòñÿ óìåíüøåíèå ñòîèìîñòè äîðîæíûõ ðàáîò, ÷òî íåèçáåæíî âåäåò ê
ïðèìåíåíèþ îïòèìàëüíîé ìèðîâîé òåõíîëîãèè
îáñëóæèâàíèÿ äîðîã, ïðè êîòîðîé ñâîåâðåìåííîå ñîäåðæàíèå îòîäâèãàåò ñðîêè ðåìîíòà è ðåêîíñòðóêöèè, óìåíüøàÿ ïðè ýòîì ñðåäíþþ ñòîèìîñòü îáñëóæèâàíèÿ äîðîã.
Êîýôôèöèåíò ýôôåêòèâíîñòè óïðàâëåíèÿ
k ýô =
k ýô min =
(1 + k ýò )
Ì ñ + Ì ð + Ì ðåê
Ì ñ + d ð Ì ð + d ðåê Ì ðåê ,
ãäå d ðåê è d ð – êîýôôèöèåíòû ïðèâåäåíèÿ ê ðàáîòàì ïî ñîäåðæàíèþ, èìååò ìèíèìóì ïðè Ìðåê
>>(Ìð+Ìðåê):
1
d ðåê ,
à ìàêñèìóì ïðè Ìc >>(Ìð+Ìðåê):
k ýômax = 1 .
Ó÷èòûâàÿ ðàçëè÷íûå öåëåâûå óñòàíîâêè
ñðàâíèâàåìûõ ñèñòåì, ìîæíî ñ÷èòàòü, ÷òî
k ýô → k ýô min =
1
d ðåê
, à k ′ýô → k ýô max = 1.
Ïðè äîñòèæåíèè ïðåäåëüíûõ çíà÷åíèé êîýôôèöèåíòîâ ýôôåêòèâíîñòè óïðàâëåíèÿ ïîëó÷èì ïðåäåëüíîå çíà÷åíèå ýôôåêòèâíîñòè Ý:
Ýmax=dðåê(1+kýò).
Ðåàëüíî ñåáåñòîèìîñòü ðàáîò ïî ðåêîíñòðóêöèè ðàç â 20-30 âûøå ñåáåñòîèìîñòè ðàáîò
ïî ñîäåðæàíèþ, òî åñòü dðåê= 20õ30, èç-çà ÷åãî
óäåëüíûé âåñ êîýôôèöèåíòà ýôôåêòèâíîñòè óïðàâëåíèÿ â îáùåé ýôôåêòèâíîñòè ñèñòåìû âåñüìà îùóòèì.
Óïðàâëåíèå «Êðàñíîäàðàâòîäîð» (íûíå
«Äîðîæíûé êîìèòåò»), ãäå âíåäðåíà ïðåäëîæåííàÿ ñèñòåìà, â ïðîöåññå ïåðåõîäà ê ðûíî÷íûì îòíîøåíèÿì ïîñëåäîâàòåëüíî óâåëè÷èâàëî êîýôôèöèåíò k′ýô , ÷òî ïðè ðîñòå öåí íà ñòðîèòåëüíûå ìàòåðèàëû ïîçâîëèëî óäåðæèâàòü
ñðåäíþþ ñåáåñòîèìîñòü äîðîæíûõ ðàáîò íà
óðîâíå 1991 ãîäà.
Ñïèñîê èñïîëüçîâàííîé ëèòåðàòóðû:
1. Áàðàíîâñêàÿ Ò.Ï. Ìîäåëè ðåôîðìèðîâàíèÿ ïðåäïðèÿòèé ÀÏÊ â ðûíî÷íîé ýêîíîìèêå. – Êðàñíîäàð:, Èçäàòåëüñòâî ÊóáÃÀÓ 2000. – 218ñ.: èë.
2. Áàðàíîâñêàÿ Ò., Áåçðîäíûé Î. Äîðîãè â ñåëüñêîé èíôðàñòðóêòóðå // Ýêîíîìèêà ñåëüñêîãî õîçÿéñòâà – 2000, – ¹4. Ñ. 23-24.
86
ÂÅÑÒÍÈÊ ÎÃÓ 6`2004