Математическая модель процесса смачивания

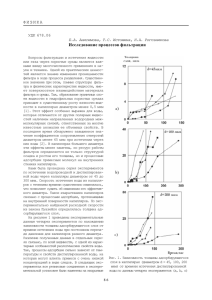
ÌÀÒÅÌÀÒÈ×ÅÑÊÀß ÌÎÄÅËÜ ÏÐÎÖÅÑÑÀ
ÑÌÀ×ÈÂÀÍÈß ÏÐÈ ÄÂÈÆÅÍÈÈ ÆÈÄÊÎÑÒÈ Â
ÂÅÐÒÈÊÀËÜÍÎÉ ÏËÎÑÊÎÑÒÈ
Îëèôåðîâè÷ Í. Ì., Ãðèíþê Ä. À., Îðîáåé È. Î.
Êàôåäðà àâòîìàòèçàöèè òåõíîëîãè÷åñêèõ ïðîöåññîâ è ýëåêòðîòåõíèêè , Áåëîðóññêèé ãîñóäàðñòâåííûé
òåõíîëîãè÷åñêèé óíèâåðñèòåò
Ìèíñê, Ðåñïóáëèêà Áåëàðóñü
E-mail: [email protected]
Äëÿ îïòèìàëüíîãî óïðàâëåíèÿ ïðîöåññàìè ñìà÷èâàíèÿ íåîáõîäèìî ïîëó÷åíèå çàêîíîâ, îïèñûâàþùèõ äàííîå ÿâëåíèå. Àâòîðàìè áûëî ðàçðàáîòàíî óñòðîéñòâî, êîòîðîå ïîçâîëÿåò ïî íàðàñòàíèþ åìêîñòè êîíäåíñàòîðà îïðåäåëÿòü âðåìÿ êàïèëëÿðíîãî âïèòûâàíèÿ òåñòîâîé áóìàãîé. Êîíñòðóêöèÿ ïåðâè÷íîãî ïðå-
Р
îáðàçîâàòåëÿ äàííîãî ïðèáîðà ïðåäóñìàòðèâàåò ðàäèàëüíîå èëè âåðòèêàëüíîå ðàñïðîñòðàíåíèå ôðîíòà
ñìà÷èâàíèÿ. Äëÿ èíòåðïðåòàöèè ïîêàçàíèé ïðèáîðà íåîáõîäèìà ìàòåìàòè÷åñêàÿ ìîäåëü, êîòîðàÿ îòîá-
БГ
УИ
ðàæàåò çàâèñèìîñòü èçìåíåíèÿ ïëîùàäè ïîâåðõíîñòè ñìî÷åííîé áóìàãè îò âðåìåíè.  äàííîé ðàáîòå
ïðåäñòàâëåíà ìîäåëü, ïîëó÷åííàÿ äëÿ ñëó÷àÿ âåðòèêàëüíîãî ðàñïðîñòðàíåíèÿ ôðîíòà.
Ââåäåíèå
f1,r = 2πr (σ12 − σ13 ) ,
(1)
ãäå σ12 , σ13 ìåæôàçíîå íàòÿæåíèå ¾òâåðäîå òåëî ãàç¿ è ¾òâåðäîå òåëî æèäêîñòü¿ ñîîòâåòñòâåííî.
Ýòà ñèëà îïðåäåëÿåòñÿ êîëè÷åñòâîì êàïèëëÿðîâ, ïðèõîäÿùèìñÿ íà ïåðèìåòð òåêóùåãî ðàñïðîñòðàíåíèÿ ôðîíòà, ò.å.
ек
а
Èññëåäîâàíèå ïîâåðõíîñòíûõ ÿâëåíèé íà
ãðàíèöàõ ðàçäåëà ñïîñîáñòâóåò èíòåíñèôèêàöèè
èçâåñòíûõ è ñîçäàíèþ íîâûõ òåõíîëîãè÷åñêèõ
ïðîöåññîâ äëÿ âûñîêîäèñïåðñíûõ ñèñòåì. Áîëüøîå çíà÷åíèå ïðèîáðåòàåò èññëåäîâàíèå ÿâëåíèé íà ãðàíèöå ðàçäåëà òâåðäîãî òåëà ñ æèäêîñòüþ. Ýòè ýôôåêòû ÿâëÿþòñÿ íà÷àëüíûìè è ñóùåñòâåííûìè ñòàäèÿìè ðàçíûõ òåõíîëîãè÷åñêèõ
ïðîöåññîâ. Ðàçðàáîòêà ìàòåìàòè÷åñêèõ ìîäåëåé
ñìà÷èâàíèÿ òâåðäîãî òåëà îòêðûâàåò íîâûå âîçìîæíîñòè óïðàâëåíèÿ ýòèìè ïðîöåññàìè [1-3].
Âêëàä ñèëû ïîâåðõíîñòíîãî íàòÿæåíèÿ îäíîãî êàïèëëÿðà èìååò âèä [4]:
f1 = 2πr (σ12 − σ13 ) lnhn,
(2)
ãäå n êîëè÷åñòâî êàïèëëÿðîâ ïî ôðîíòó ðàñïðîñòðàíåíèÿ æèäêîñòè. n ÷åðåç âåëè÷èíó ïîðèÎöåíêó äèíàìèêè ïðîöåññà âïèòûâàíèÿ ñòîñòè ìàòåðèàëà γ âûðàæàåòñÿ â âèäå:
ìîæíî ïðîèçâîäèòü ïî íàáëþäåíèþ çà ïðîöåññîì
γ = Vnn /V0 ,
(3)
ïðîïèòêè ôèëüòðîâàëüíîé áóìàãè ñ çàðàíåå èçâåñòíûìè ñâîéñòâàìè. Ðàññìîòðèì âàðèàíò äâè- ãäå Vnn = xhln2 πr2 îáúåì ïîðîâîãî ïðîæåíèÿ æèäêîñòè ïî êàïèëëÿðàì ïîðèñòîãî òåëà ñòðàíñòâà ïî ôðîíòó ðàñïðîñòðàíåíèÿ æèäêîñòè, V0 = xhl îáúåì îáðàçöà, ñìî÷åííûé æèäâ âåðòèêàëüíîé ïëîñêîñòè (ñì.ðèñ. 1).
êîñòüþ. Òîãäà ôîðìóëà (3) ïðèìåò âèä:
Би
бл
ио
т
Îñíîâíàÿ ÷àñòü
γ=
xyln2 πr2
= n2 πr2 .
xyl
Âûðàçèâ n è ïîäñòàâèâ â (2), ïîëó÷èì:
f1 = 2πr (σ12 − σ13 )
ãäå
2lhγ
(σ12 − σ13 )
(4)
r
êîýôôèöèåíò, êîòîðûé îïðåäåëÿåòñÿ ïàðàìåòðàìè áóìàãè (òîëùèíîé, ïîðèñòîñòüþ è ðàçìåðàìè
ïîð), à òàêæå êîýôôèöèåíòàìè ìåæôàçíîãî íàòÿæåíèÿ ¾òâåðäîå òåëî ãàç¿ è ¾òâåðäîå òåëî
æèäêîñòü¿. Èç ïîëó÷åííîãî ðåçóëüòàòà âèäíî,
÷òî âêëàä ñèëû ïîâåðõíîñòíîãî íàòÿæåíèÿ ÿâëÿåòñÿ âåëè÷èíîé ïîñòîÿííîé è íå áóäåò çàâèñèòü
îò óðîâíÿ ïîäúåìà ôðîíòà ñìà÷èâàíèÿ x.
Äåéñòâèå ñèëû òÿæåñòè áóäåò îïðåäåëÿòü
äàâëåíèå æèäêîñòè ρgx, êîòîðàÿ ïåðåìåùàåòñÿ
A1 =
Ðèñ. 1 Ãåîìåòðè÷åñêèå ïàðàìåòðû èçìåðèòåëüíîãî
ïðåîáðàçîâàòåëÿ
Îáðàçåö ôèëüòðîâàëüíîé áóìàãè èìååò òîëùèíó h, øèðèíó l, ñ îñíîâíûì ýôôåêòèâíûì ðàçìåðîì êàïèëëÿðà r. Ñîãëàñíî ïîðèñòîñòè γ íà
1 ìåòð äëèíû ïîìåùàåòñÿ n êàïèëëÿðîâ ðàäèóñîì r.
lhγ
2lhγ
=
(σ12 − σ13 ) = A1 ,
2
r π
r
224
ïî êàïèëÿðàì ôèëüòðîâàëüíîé áóìàãè, ãäå ρ ïëîòíîñòü æèäêîñòè, g óñêîðåíèå ñâîáîäíîãî
ïàäåíèÿ, õ óðîâíü ïîäúåìà ôðîíòà ñìà÷èâàíèÿ. Ýòà ñèëà áóäåò çàìåäëÿòü ïðîöåññ âïèòûâàíèÿ, åå âêëàä ìîæíî ïðåäñòàâèòü:
f2 = P S = ρgxS,
(5)
èç çàêîíà ñîõðàíåíèÿ ìîìåíòà èìïóëüñà ñëåäóåò, ÷òî íåîáõîäèìî ó÷èòûâàòü ìàññó òîëüêî òåõ
êàïèëëÿðîâ, êîòîðûå ñîïðèêàñàþòñÿ íåïîñðåäñòâåííî ñ ñîñóäîì. Ò.å
γ
m = ρV = ρlhn2 xπr2 = ρlh 2 xπr2 = ρlhγx = F1 x,
r π
ãäå
F1 = ρlhγ.
(11)
Р
ãäå S ñóììàðíàÿ ïëîùàäü ýòèõ êàïèëëÿðîâ. S
ìîæíî ðàññ÷èòàòü ïî ôîðìóëå:
Òîãäà
γ
2
2
2
2
dm
S = nhnlπr = n hlπr = 2 hlπr = hlγ.
= F1 ẋ.
(12)
r π
dt
Îêîí÷àòåëüíî âûðàæåíèå äëÿ äåéñòâèÿ ñèÏîäñòàâèâ çíà÷åíèÿ ñèë f1 , f2 , f3 , à òàêæå
ëû òÿæåñòè ïðèìåò âèä:
âûðàæåíèå, ïîëó÷åííîå äëÿ ìàññû m, â óðàâíåíèå (10), ïîëó÷èì:
f2 = ρgxγhl = xC1 ,
A1 − xC1 − D1 xẋ = F1 ẋ2 + F1 xẍ.
ãäå
а
БГ
УИ
C1 = ρgγhl.
(6)
Ïðåîáðàçóåì ïîëó÷åííîå âûðàæåíèå:
Ïðè ðàñ÷åòå äèíàìèêè âïèòûâàíèÿ äëÿ ó÷åẋ2
1 A1
C1
D1
ẋ −
+
−
ẍ = −
òà âëèÿíèÿ äâèæåíèÿ æèäêîñòè â êàïèëëÿðàõ
F1
x
x F1
F1
ïðèíèìàþò óñëîâèå î êâàçèñòàöèîíàðíîì òå÷åÏîäñòàâèâ çíà÷åíèÿ êîýôôèöèåíòîâ (4),
íèè (ò. å. äëÿ áîëüøèõ âðåìåí t ) è ïîëüçóþòñÿ
(6),
(9),
(11), ïîëó÷èì:
ôîðìóëîé Ïóàçåéëÿ:
ẋ2
1 2∆σ
8η
f3 = −8πη xẋ.
(7)
+
−g
ẍ = − 2 ẋ −
r ρ
x
x rρ
Èñïîëüçóåì ñëåäóþùóþ ñèñòåìó ïîñòðîåèëè
íèÿ êàïèëëÿðîâ â áóìàãå (ñì. ðèñ. 2).
ẋ2
1
ẍ = −b0 ẋ −
+ b1 − b2 .
x
x
Âûïîëíèâ ïîäñòàíîâêó
ек
x = exp(y); ẋ = ẏ exp(y); ẍ = ÿ exp(y)+ẏ 2 exp(y),
ïîëó÷èì:
т
ÿ = −b0 ẏ − 2ẏ 2 +
1
b2
b1 −
.
exp(2y)
exp(y)
(13)
Çàêëþ÷åíèå
Би
бл
ио
Ðåøåíèå ïîëó÷åííîãî íåëèíåéíîãî äèôôåðåíöèàëüíîãî óðàâíåíèÿ (13) ïîçâîëÿåò ïîëó÷èòü çàâèñèìîñòü ôðîíòà ðàñïðîñòðàíåíèÿ ñìîÐèñ. 2 Ñèñòåìà ïîñòðîåíèÿ êàïèëëÿðîâ ïðè
÷åííîé ïîâåðõíîñòè áóìàãè îò âðåìåíè ïðè âåðâåðòèêàëüíîì ðàñïðîñòðàíåíèè æèäêîñòè
òèêàëüíîì ðàñïîëîæåíèè îáðàçöà. Ïîëó÷åííàÿ
Îòäåëüíûå êàïèëëÿðû îäèíàêîâû, èìåþò ìîäåëü ìîæåò áûòü èñïîëüçîâàíà äëÿ èíòåðïðåäëèíó x0 è ñå÷åíèå Sr , ïðè÷åì êîëè÷åñòâî êàïèë- òàöèè ïîêàçàíèé ïðèáîðà íåïðåðûâíîãî èçìåëÿðîâ â êàæäîì èç ðÿäîâ îäèíàêîâî. Èñõîäÿ èç ðåíèÿ ïðîöåññà ñìà÷èâàíèÿ [5] ïðè èñïîëüçîâàíèè ïåðâè÷íîãî ïðåîáðàçîâàòåëÿ ñ âåðòèêàëüôîðìóëû Ïóàçåéëÿ äëÿ îäèíî÷íîãî êàïèëëÿðà
íûì ðàñïðîñòðàíåíèåì ôðîíòà ñìà÷èâàíèÿ.
f3,r = −8πη x0 ẋ.
(8)
Ñèëà âÿçêîãî òå÷åíèÿ äëÿ âñåãî ñìî÷åííî1.
ãî ó÷àñòêà áóìàãè îïðåäåëÿåòñÿ ñóììîé âêëàäîâ
êàæäîãî ðÿäà â ñèëó âÿçêîãî òå÷åíèÿ:
X
8ηγhl
2.
f3 =
f3,r,i = − 2 xẋ = −D1 xẋ,
r
3.
ãäå
8ηγhl
D1 =
.
(9)
r2
4.
Ðàâíîäåéñòâóþùàÿ òðåõ ñèë
d
dm
5.
f = f1 − f2 + f3 =
(mẋ) =
ẋ + mẍ. (10)
dt
dt
Âåëè÷èíà m áóäåò îïðåäåëÿòüñÿ êîëè÷åñòâîì æèäêîñòè â êàïèëëÿðàõ. Âñëåäñòâèå òîãî,
÷òî ñêîðîñòü è óñêîðåíèå áóäóò íåðàâíîìåðíûìè, è ñ óäàëåíèåì îò êðàÿ áóäóò óìåíüøàòüñÿ,
225
Ñïèñîê ëèòåðàòóðû
Ñóìì, Á. Ä. Ôèçèêî-õèìè÷åñêèå îñíîâû ñìà÷èâàíèÿ
è ðàñòåêàíèÿ / Á. Ä. Ñóìì, Þ. Â. Ãîðþíîâ Ì.:
Õèìèÿ, 1976. 232 ñ.
Áûõîâñêèé, À. È. Ðàñòåêàíèå / À. È. Áûõîâñêèé. Êèåâ: Íàóê. äóìêà, 1983. 192 ñ.
Waschburn, E. W. The dynamics of capillary ow /
E. W. Waschburn // Phys. Rev. 1921. 17. P. 273283.
Äåðÿãèí, Á. Â. Ñêîëüæåíèå æèäêîñòåé â êàïèëëÿðàõ / Á. Â. Äåðÿãèí, Í. Í. Ôåäÿêèí // Äîêë. ÀÍ
ÑÑÑÐ. - 1968.  6, ñ. 1300 1302.
Ãðèíþê, Ä. À. Óñòðîéñòâî íåïðåðûâíîãî èçìåðåíèÿ
ïðîöåññà ñìà÷èâàíèÿ/ Ä. À. Ãðèíþê, È. Î. Îðîáåé, Í. Ì. Áîãîñëàâ // Òðóäû ÁÃÒÓ. Ñåð. VI, Ôèç.ìàò. íàóêè è èíôîðìàòèêà. 2011. Âûï. XVIII. Ñ.108112.