Элементарная алгебра с точки зрения высшей математики (1 год обучения) 1.

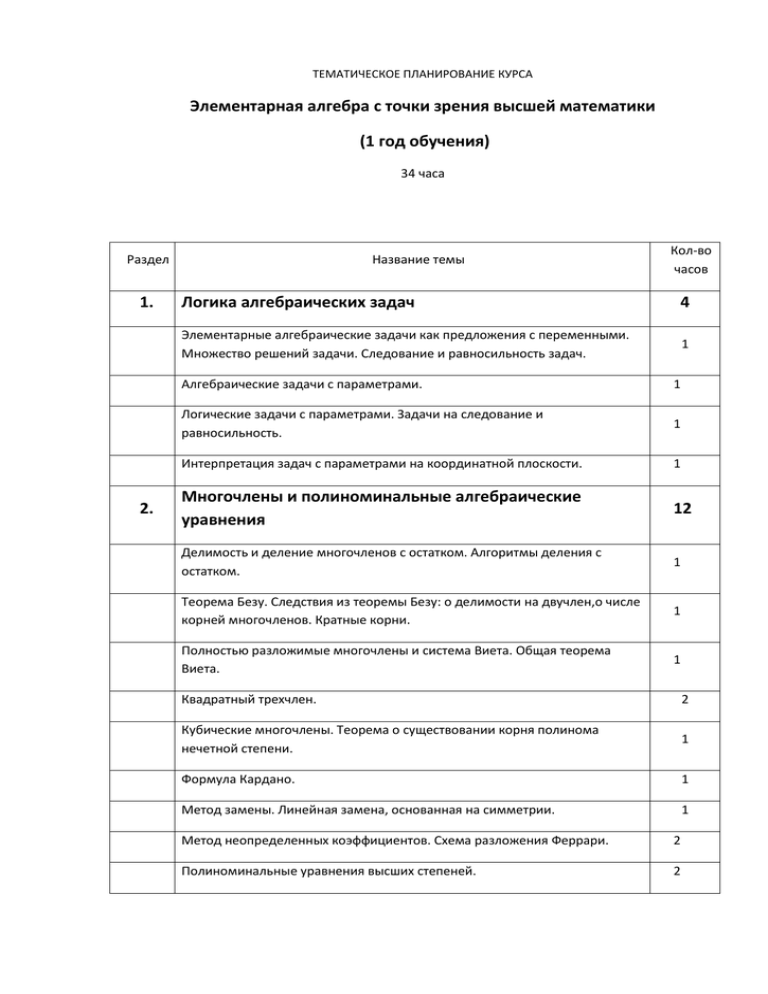
ТЕМАТИЧЕСКОЕ ПЛАНИРОВАНИЕ КУРСА
Элементарная алгебра с точки зрения высшей математики
(1 год обучения)
34 часа
Раздел
1.
2.
Название темы
Кол-во
часов
Логика алгебраических задач
4
Элементарные алгебраические задачи как предложения с переменными.
Множество решений задачи. Следование и равносильность задач.
1
Алгебраические задачи с параметрами.
1
Логические задачи с параметрами. Задачи на следование и
равносильность.
1
Интерпретация задач с параметрами на координатной плоскости.
1
Многочлены и полиноминальные алгебраические
уравнения
12
Делимость и деление многочленов с остатком. Алгоритмы деления с
остатком.
1
Теорема Безу. Следствия из теоремы Безу: о делимости на двучлен,о числе
корней многочленов. Кратные корни.
1
Полностью разложимые многочлены и система Виета. Общая теорема
Виета.
1
Квадратный трехчлен.
2
Кубические многочлены. Теорема о существовании корня полинома
нечетной степени.
1
Формула Кардано.
1
Метод замены. Линейная замена, основанная на симметрии.
1
Метод неопределенных коэффициентов. Схема разложения Феррари.
2
Полиноминальные уравнения высших степеней.
2
3.
Рациональные алгебраические уравнения, неравенства и
их системы
18
Симметрические, кососимметрические и возвратные многочлены и
уравнения.
2
Общие схемы решения дробно-рациональных уравнений и неравенств.
2
Метод оценки. Использование монотонности.
2
Неравенства с двумя переменными. Метод областей.
2
Уравнение с несколькими переменными. Рациональные уравнения с
двумя переменными. Однородные уравнения с двумя переменными.
2
Рациональные алгебраические системы. Однородные системы уравнений с
двумя переменными.
2
Замена переменных в системах уравнений.
1
Симметрические выражения от двух переменных. Теорема Варинга- Гаусса
о представлении симметрических многочленов через элементарные
симметрические многочлены.
1
Система Виета и симметрические системы с двумя переменными.
1
Системы с тремя переменными. Основные методы.
1
Метод оценок. Метод разложения.
2
ТЕМАТИЧЕСКОЕ ПЛАНИРОВАНИЕ КУРСА
Элементарная алгебра с точки зрения высшей математики
(2 год обучения)
34 часа
Раздел
4.
5.
Название темы
Кол-во
часов
Иррациональные алгебраические задачи.
18
Представление об иррациональных алгебраических функциях.
1
Уравнения с квадратными радикалами. Замена переменной. Замена с
ограничениями.
1
Неэквивалентные преобразования. Сущность проверки.
1
Метод оценки. Использование монотонности. Использование
однородности.
1
Иррациональные алгебраические неравенства. Эквивалентные
преобразования неравенств.
2
Дробно-иррациональные неравенства.
2
Замена при решении иррациональных неравенств.
2
Уравнения с модулями. Схемы решений уравнений с модулями.
2
Неравенства с модулями. Схемы решений неравенств с модулями.
2
Иррациональные алгебраические системы. Основные приемы.
2
Смешанные системы с двумя переменными.
2
Разные задачи с параметрами.
16
Аналитический подход. Рациональные задачи с параметрами.
2
Аналитический подход. Иррациональные задачи с параметрами.
2
Задачи с модулями и с параметрами. Критические значения параметра.
2
Метод интервалов, метод разложения, метод замены в задачах с
параметрами.
2
Системы с параметром.
2
Метод областей в решении задач с параметрами.
2
Метод координат при решении задач с параметром.
2
Применение производной при решении задач с параметром.
2
Список литературы
«Методика обобщающих повторений при обучении математике». В.А. Далингер.
« Задачи по математике. Уравнения и неравенства». Вавилов В.В., Мельников И.И.
«Факультативный курс по математике. Решение задач». 10-11 класс. Шарыгин.
« Задачи по математике для подготовки к тестированию и ЕГЭ». Вольпер Е. И., Федорова.
«Пособие по математике для подготовки к тестированию» Королева, Нейман.
Цикл статей в газете «Математика» (приложении к газете «Первое сентября».)
Материалы Четверговой школы. Составитель Е.И. Федорова.
Материалы авторских курсов Е.И.Вольпера «Задачи на вступительных экзаменах в ВУЗ».
Амелькин В.В., Рабцевич В.Л. Задачи с параметрами. Справ.пособие по математике. - Мн.: Асар,
1996.
Горнштейн П.И., Полонский В.Б., Якир М.С. Задачи с параметрами. - М.: Илекса,Гимназия, 1998.
Тиняков И.Г. Задачи с параметрами. М.: 2001.
Натяганов В.Л., Лужина Л.М. Методы решения задач с параметрами: Учеб. пособие.-М.: Изд-во
МГУ, 2003.
Журнал «Математика в школе» №10 2003 г., № 4, № 5 2004 г., № 4 2005