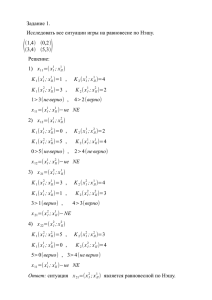Теория игр - Саратовский государственный университет

Саратовский государственный университет им. Н.Г Чернышевского
Кафедра теории вероятностей,
математической статистики и
управления стохастическими
процессами
Теория игр
Составители курса:
1. Теоретический материал: Луньков А.Д.
2. Вопросы для самоконтроля: Луньков А.Д.
3. Тестовые задания: Луньков А.Д.
Саратов 2008 г.
Оглавление ВВЕДЕНИЕ......................................................................................................................... 3
1. ПРИНЯТИЕ РЕШЕНИЯ В УСЛОВИЯХ НЕОПРЕДЕЛЕННОСТИ.................. 4
2. ПРИНЯТИЕ РЕШЕНИЯ В УСЛОВИЯХ РИСКА .................................................. 8
3. АНТАГОНИСТИЧЕСКИЕ ИГРЫ .......................................................................... 13
4. ТЕОРИЯ МАТРИЧНЫХ ИГР .................................................................................. 20
5. МЕТОДЫ РЕШЕНИЯ МАТРИЧНЫХ ИГР.......................................................... 29
6. БИМАТРИЧНЫЕ ИГРЫ .......................................................................................... 42
Вопросы для самоконтроля по курсу "Теория игр" ............................................... 53
Задачи для самостоятельного решения ...................................................................... 57
Тесты по курсу "Теория игр" ....................................................................................... 59
СПИСОК РЕКОМЕНДУЕМОЙ ЛИТЕРАТУРЫ ..................................................... 70
ВВЕДЕНИЕ
Игра - это идеализированная математическая модель
коллективного поведения: несколько игроков влияют на исход
игры, причем их интересы различны.
Э. Мулен
Что общего у шахмат, карточных игр, войн, переговоров, рыночной
конкуренции, аукционов? Все эти ситуации можно описать c помощью
теории игр - раздела прикладной математики, ставшей неотъемлемой частью
экономической теории. Всюду, где только имеет место взаимодействие
самостоятельных рациональных (или частично рациональных) субъектов,
возникает игра. Главный вопрос теории игр заключается в предсказании
поведения участников игры: какие ходы сделают шахматисты, чем
завершатся войны и переговоры, какие цены сформируются на рынке и т.д.
Оказывается, теория игр позволяет сделать достаточно сильные
предсказания. Механизмы конкуренции, функционирования рынка,
возникновения или краха монополий, способы принятия ими решений в
условиях конкурентной борьбы, то есть механизмы игры монополий,
действующие в экономической реальности, - все это является предметом
анализа теории игр. Уже в момент ее зарождения многие предсказали
революцию в экономических науках благодаря использованию нового
подхода. Революции, возможно, и не произошло, но тенденции развития
экономики показал плодотворность методов теории игр в прикладной сфере.
Так, в 1994 году Дж. Харшаньи и Р. Зельтен получили Нобелевскую премию
по экономике за работы в области теории игр (приложения их исследований,
например – переговоры с односторонними трансакционными затратами,
равновесие рынка с продавцом и несколькими потенциальными
покупателями).
Теория игр имеет не очень длинную историю. Решающий поворот в ее
развитии произошел в 1928 году благодаря американцу Дж. фон Нейману.
Именно тогда он представил математическое обоснование общей стратегии
для игры двух участников в терминах минимизации и максимизации. Одним
из родоначальников теории игр был и французский математик Э. Борель. Но
первым систематизированным изложением идей и методов в этой области
была вышедшая в 1944 году работа фон Неймана и О. Моргенштерна
"Теория игр и экономическое поведение", которая распространила теорию
игр на произвольное число участников и применила эту теорию к
экономическому поведению. Предложенная в ней стратегия - "минимакс",
или минимизация максимальных потерь, - определяется как рациональный
курс в условиях неопределенности.
Теория игр и решений получила сильный импульс в годы второй
мировой войны, когда был введен термин "исследование операций". В
типичной задаче этой тематики рассматривалась "дуэль" между самолетом и
подводной лодкой. Первому требовалось найти оптимальную схему
патрульного поиска в определенном районе; другой было необходимо
изыскать наилучший способ уйти от наблюдения. Математики Группы
исследования операций по противолодочной защите, используя материалы
фон Неймана, относящиеся к 1928 году, решили эту задачу.
Статистические критерии для принятия решений в условиях
неопределенности были обоснованы математиком из Колумбийского
университета А. Вальдом в 1939 году. Они определяют "максимин" критерий, которым пользуются в ожидании наихудшего результата. Л.
Гурвиц и Л. Сэвидж разработали и другие критерии, подобные "критериям
сожаления", где субъективные вероятности могут заставить увеличить или
уменьшить риск.
Обычно теория игр определяется как теория математических моделей
выбора оптимальных решений в условиях неопределенности. При этом тип
неопределенности, изучаемый в теории игр, характеризуется тем, что
рассматриваются ситуации, исход в которых определяется действием
нескольких сторон, каждая из которых преследует собственные цели (такие
взаимодействия нескольких сторон называются играми). Несовпадение целей
действующих сторон, а также определенные ограничения на обмен
информацией между ними, приводят к тому, что эти взаимодействия носят
конфликтный характер, поэтому в прикладном аспекте теория игр может
рассматриваться как наука о рациональном поведении в условиях конфликта.
Очевидно, что взаимодействия между производителями и
потребителями, из которых фактически складывается экономическая
реальность, имеют именно такой характер, как указано выше, поэтому теория
игр является наиболее адекватной теорией для изучения экономического
поведения. Следует иметь в виду, что теория игр изучает не фактическое
поведение участников, а их гипотетическое поведение, направленное на
получение наилучшего в некотором смысле (оптимального) результата.
В настоящем пособии мы ограничиваемся рассмотрением той части
теории игр, которая связана с приложениями в экономике. Игры более чем
двух игроков в пособие не включены. Представлены следующие классы
теоретико-игровых моделей: игры с природой, антагонистические игры,
биматричные игры.
1. ПРИНЯТИЕ РЕШЕНИЯ В УСЛОВИЯХ НЕОПРЕДЕЛЕННОСТИ
Системное описание задачи принятия решения в условиях
неопределенности состоит в следующем. Имеется некоторая система, в
которой выделена управляющая подсистема, и вся система погружена в
некоторую среду. Управляющая подсистема может воздействовать на
систему с помощью альтернативных управляющих воздействий, приводящих
к изменению состояния этой системы. Выбор управляющего воздействия
происходит в соответствии с целями управляющей подсистемы. Принятие
решения, то есть выбор одной из имеющихся альтернатив, - является
центральным моментом управления.
Состояние системы определяется двумя факторами: выбранным
управляющим воздействием со стороны управляющей подсистемы и
состоянием среды.
Математическая модель задачи принятия решения (далее – ЗПР) в
условиях неопределенности представляет собой формализацию указанной
конструкции. Пусть Х – множество управляющих воздействий (альтернатив)
управляющей подсистемы. Y – множество состояний среды. В соответствии
со сказанным выше, состояние системы однозначно определяется парой (x,y),
где x∈X и y∈Y. Управляющая подсистема оценивает каждое состояние
системы некоторым числом, выражающим "полезность" этого состояния для
управляющей подсистемы; таким образом, возникает функция F: X×Y→R.
Значение функции F(x,y) есть оценка полезности (с точки зрения
управляющей подсистемы) того состояния системы, которое возникает, если
управляющая подсистема выбирает управляющее воздействие х, а среда
принимает состояние у. Принципиальным является то обстоятельство, что
при принятии решения управляющая система "не знает", в каком состоянии
находится среда, то есть она не имеет информации о наличном состоянии
среды. Именно это обстоятельство имеют в виду, когда говорят, что
принятие решения происходит в условиях неопределенности. Отметим, что
эта неопределенность не является абсолютной, так как принимающему
решение известно множество состояний среды (то есть множество Y) и
известна функция F(x,y).
В теории игр описанную выше ЗПР называют игрой с природой, причем
управляющую подсистему принято называть игроком, выбираемые им
альтернативные воздействия – стратегиями, а функцию F(x,y) – функцией
выигрыша игрока. Таким образом, в теоретико-игровой терминологии задача
принятия решения в условиях неопределенности формулируется следующим
образом. Пусть Х – множество стратегий игрока, Y – множество состояний
среды (природы), F(x,y) – функция выигрыша игрока. Требуется указать
наилучшую в некотором смысле альтернативу, или, как говорят в теории игр,
найти оптимальную стратегию. Подчеркнем еще раз, что основная
сложность данной задачи, носящая принципиальный характер, связана с
отсутствием у игрока информации о состоянии среды (если бы игрок такую
информацию имел, то его функция выигрыша стала бы функцией одной
переменной х и задача нахождения оптимальной стратегии превратилась бы в
задачу нахождения наибольшего значения этой функции).
В случае, когда и Х, и Y конечны, функцию выигрыша F(x,y) удобно
задавать в виде матрицы A = (ai j ) , i = 1, n , j = 1, m , считая Х={1,…,n},
Y={1,…,m}; при этом ai j есть значение функции выигрыша F в ситуации,
когда игрок выбирает стратегию i, а среда принимает состояние j.
Замечание. Так как в математической модели "природа" стратегий
игрока и состояний среды несущественна, удобно различать их по номерам,
полагая Х={1,…,n}, Y={1,…,m}.
Изложим основные принципы, по которым из конечного множества
стратегий выбираются оптимальные. Далее в 1-й и 2-й главах мы будем
рассматривать только конечные множества.
Надо иметь некоторый способ сравнения двух стратегий. Самый
простой и естественный принцип, по которому можно их сравнить - это
принцип доминирования, состоящий в следующем: стратегия i1 называется
доминирующей стратегию i2 (записывается i1≥ i2), если при любом состоянии
среды выигрыш игрока при выборе им стратегии i1 будет не меньше, чем
≥a
при всех j=1,…,m).
выигрыш при выборе стратегии i2 (то есть a
i1 j
i2 j
Очевидно, что если i1≥ i2, то независимо от состояния среды стратегия i1
является лучшей для игрока, чем стратегия i2, поэтому стратегию i2 можно
исключить из дальнейшего рассмотрения. Итак, принцип доминирования
состоит в том, что исключаются доминируемые стратегии.
Для того, чтобы выбрать из оставшихся стратегий оптимальную,
нужны какие-то дополнительные соображения.
Основной метод, позволяющий найти оптимальную стратегию в ЗПР в
условиях неопределенности, состоит в следующем:
формулируется некоторая гипотеза о поведении среды, позволяющая
дать единственную численную оценку каждой стратегии. Оптимальной
считается та стратегия, для которой численная оценка является
максимальной.
Заметим, что задание оценки каждой стратегии позволяет сравнить
любые две стратегии: из двух стратегий лучшей считается та, которая имеет
большую оценку (стратегии, имеющие одинаковую численную оценку,
считаются эквивалентными). Таким образом, задание оценок стратегий
устанавливает критерий для сравнения стратегий. Рассмотрим теперь
важнейшие критерии, используемые для задач принятия решений в условиях
неопределенности.
КРИТЕРИЙ ЛАПЛАСА L основан на гипотезе равновероятности и
содержательно может быть сформулирован следующим образом: «поскольку
мы ничего не знаем о состояниях среды, их надо считать равновероятными».
Иногда этот принцип называется также принципом недостаточного
основания. При принятии данной гипотезы в качестве оценки стратегии i
надо брать соответствующий ей средний выигрыш, то есть
1 m
L(i ) =
∑ a .
m j =1 i j
Оптимальная по данному критерию стратегия L0 находится из условия
L(i ) = max L(i) .
0
1≤i≤n
КРИТЕРИЙ ВАЛЬДА V основан на гипотезе крайней осторожности
(крайнего пессимизма), которая формулируется так: "При выборе той или
иной стратегии надо рассчитывать на худший из возможных вариантов".
Если принять эту гипотезу, то оценкой стратегии i является число
V (i ) = min aij . Оптимальная по данному критерию стратегия i0 находится
1≤ j ≤m
из условия V (i0 ) = max V (i ) , то есть min aij = max min aij .
1≤i≤n
1≤ j ≤ m
1≤i ≤ n1≤ j ≤ m
Принцип оптимальности, основанный на критерии Вальда, называется
принципом максимина.
Замечание. Если значения функции выигрыша имеют характер потерь
(то есть, фактически они являются не выигрышами, а проигрышами), то
оценкой стратегии i является max a , а оптимальной будет та стратегия
ij
1≤ j ≤ m
i0, при которой указанный максимум достигает наименьшего значения, то
есть
max ai j = min max aij . Такая стратегия i0 называется
1≤i ≤n 1≤ j ≤m
1≤ j ≤m 0
минимаксной, а соответствующий принцип оптимальности называется
принципом минимакса.
КРИТЕРИЙ ГУРВИЦА G связан с введением числа 0≤ α ≤1,
называемого "показателем пессимизма-оптимизма". Гипотеза о поведении
среды состоит в том, что наихудший вариант реализуется с вероятностью α ,
а наилучший - с вероятностью 1- α . Тогда оценкой стратегии i является число
G (i ) = α min aij + (1 − α ) max aij , а оптимальная стратегия i0
1≤ j ≤ m
1≤ j ≤ m
находится из условия G (i0 ) = max G (i ) . Ясно, что при α =1 данный
1≤ i ≤ n
критерий превращается в критерий крайнего пессимизма (то есть в критерий
Вальда), а при α =0 - в критерий крайнего оптимизма. Содержательная
трудность при использовании критерия Гурвица - назначение показателя
пессимизма α .
Известны и другие критерии. Критерий Сэвиджа определяется так:
S (i ) = max ( max akj − aij ) .
1≤ j ≤ m 1 ≤ k ≤ n
В отличие от предыдущих критериев, оптимальная стратегия – та, что
минимизирует значение S(i). Этот критерий - мера сожаления о незнании
истинного состояния среды.
Критерий Ходжа-Лемана –линейная
комбинация критериев Вальда и
математического ожидания . Более
сложным образом рассчитываются критерии Гермейера и произведения.
Замечание. В общем случае оптимальные решения, полученные по
указанным критериям, могут не совпадать (как говорят, критерии
противоречат друг другу). Это неудивительно, ибо эти критерии основаны на
разных гипотезах. Вводя ту или иную гипотезу, мы тем самым "снимаем
неопределенность", однако, гипотеза является только предположением, а не
знанием. Было бы странно, если бы различные предположения приводили
всегда к одному и тому же результату.
2. ПРИНЯТИЕ РЕШЕНИЯ В УСЛОВИЯХ РИСКА
Построение математической модели задачи принятия решения сводится к
заданию функции выигрыша F. Формально функция выигрыша есть функция
двух переменных х и у, но эти переменные входят в нее неравноправно, что
является отражением неравноправия управляющей системы и среды. Дело в
том, что управляющая система имеет цель, поэтому ее поведение носит
целенаправленный характер; в то же время среда (которую можно
рассматривать как обобщенный аналог природы), цели не имеет, и ее
поведение носит недетерминированный характер. Если в этой
недетерминированности имеются какие-то закономерности, они являются
закономерностями стохастического типа. В общем случае это обстоятельство
проявляется в том, что существует некоторая вероятностная мера, в
соответствии с которой появляются те или иные состояния среды. В том
простейшем случае, который мы рассматриваем, множество состояний среды
Y является конечным, и в этом случае задание вероятностной меры на
множестве Y сводится к заданию вероятностного вектора y 0 = ( y 01 ,..., y 0m ) ,
m
где y 0 j ≥ 0, ∑ y 0 j = 1; при этом y 0 j есть вероятность появления состояния j.
j =1
Вектор y0
называется априорным распределением вероятностей на
множестве состояний природы.
Предположим, что управляющей подсистеме (игроку) известен
вероятностный вектор y0 , то есть для каждого возможного состояния среды
известна вероятность его наступления. В этом случае говорят, что принятие
решения происходит в условиях риска. Пусть функция выигрыша задана в
виде матрицы A=(aij). При принятии решения в условиях риска игрок,
выбирая стратегию i, получает выигрыш aij с вероятностью y 0 j (j =1,…,m).
Таким образом, исходом, соответствующим выбору стратегии i, является
случайная величина, распределение которой задано следующим рядом:
ξi
ai1
P
y 01
…
ai j
y0 j
…
ai m
y 0m
Взяв в качестве числовой оценки i-й стратегии математическое
ожидание случайной величины ξi, получаем следующий
КРИТЕРИЙ МАТЕМАТИЧЕСКОГО ОЖИДАНИЯ М. В задаче
принятия решения в условиях риска в качестве оценки стратегии i выступает
математическое ожидание соответствующей ей случайной величины ξi. В
явном виде.
m
M ( i ) = ∑ a ij y 0 j .
j =1
В соответствии с этим правилом оптимальная стратегия игрока i0
находится из условия
m
m
M ( i0 ) = max M ( i ) или ∑ ai j y 0 j = max ∑ aij y 0 j .
1≤ i ≤ n
1≤ i ≤ n j =1
j =1 0
Как известно из теории вероятностей, математическое ожидание М(i)
представляет собой величину, к которой будет приближаться средний
выигрыш игрока при выборе им стратегии i с ростом числа испытаний, то
есть при многократном повторении игры (в предположении, что условия
игры сохраняются, т.е. вероятность наступления состояний среды остается
одной и той же). Стратегия i0, определяемая из данного условия, называется
байесовской стратегией для априорного распределения y , а подход к
0
решению игр с природой, основанный на критерии М - байесовским
подходом.
Очевидно, в основе каждого из рассмотренных в этой и предыдущей
главах критериев лежит некоторое, и достаточно сильное, упрощение
ситуации. Выбор же критерия лежит за рамками теории игр. Теория принятия
решений дает рекомендации лишь для определенного критерия. Было бы
неразумно принимать решение, не обосновав применение какого-то одного
критерия. Потому в случае, когда нет весомых причин использовать
определенный критерий (нет гипотез о поведении среды) желательно (хотя
бы и в учебных целях) подсчитать значения нескольких критериев и
проинтерпретировать полученные результаты. Достаточно важной является
теория принятия решения в условиях риска с проведением эксперимента.
Эксперимент, исходы которого стохастически связаны с состояниями
природы, может положительно повлиять на правильность решения. Эта
теория не рассматривается в данном пособии.
Пример 2.1. Режим проверок наличия вируса.
При работе ЭВМ необходимо периодически приостанавливать
обработку информации и проверять ЭВМ на наличие в ней вирусов.
Приостановка в обработке информации приводит к определённым
экономическим издержкам. Если же вирус не будет вовремя обнаружен,
возможна потеря и некоторой части информации, что приведёт к ещё
большим убыткам.
Варианты решения таковы:
Е1 – полная проверка; Е2 – минимальная проверка; Е3 – отказ от
проверки.
ЭВМ может находиться в следующих состояниях:
F1 – вирус отсутствует; F2 – вирус есть, но он не успел повредить
информацию; F3 – есть файлы, нуждающиеся в восстановлении.
Затраты на поиск вируса и его ликвидацию, а также затраты, связанные с
восстановлением информации ( A = ( a i j ) , i = 1,..,3 , j = 1,..,3 ) приведены в
первых трех столбцах таблицы 2.1. По этим значениям a ij рассчитываются
значения критериев Вальда, Лапласа, Гурвица (максимальные значения
критериев выделены полужирным шрифтом).
− 20 − 22 − 25
1 3
≈ −22.33 .
∑ a1 j =
3
3 j =1
V (1) = min a1 j = min{−20,−22,−25} = −25.
1≤ j ≤3
α = 0.2 ⇒ G (1) = α min a1 j + (1 − α ) max a1 j =
1≤ j ≤ 3
1≤ j ≤ 3
= 0.2 ⋅ ( −25) + 0.8 ⋅ (−20) = −21.
α = 0.8 ⇒ G (1) = α min a1 j + (1 − α ) max a1 j =
1≤ j ≤ 3
1≤ j ≤ 3
= 0.8 ⋅ ( −25) + 0.2 ⋅ (−20) = −24.
Аналогичным образом рассчитываются значения критериев при i=2 или 3.
L( 1 ) =
Таблица 2.1
Стратегия
F1
F2
E1
E2
E3
-20
-14
0
F3
-22
-23
-24
Критерий
Вальда
-25
-31
-40
Критерий
Лапласа
-25
-31
-40
Критерий Гурвица
α =0.2
α =0.8
-22.33
-21
-22.66
-17.4
-21.33
-8
-24
-27.6
-32
Согласно критерию Вальда следует проводить полную проверку.
Критерий Лапласа, в предположении, что все состояния машины
равновероятны, рекомендует отказаться от проверки. Рекомендации по
критерию Гурвица зависят от значения параметра α . Таким образом,
необходимо подумать о том, какая из гипотез о поведении среды более
обоснована.
Пример 2.2. Выбор проекта отеля.
Предприниматель намерен взять в аренду отель сроком на 1 год.
Имеются отели четырех типов: на 20, 30, 40 или 50 комнат. По условию
аренды предприниматель должен оплатить все расходы, связанные с
содержанием отеля. Эти расходы (в немецких марках) состоят из трех частей.
1) Расходы, не зависящие от выбора проекта отеля:
а) благоустройство территории - 10 тыс. ДМ;
б) затраты на текущий ремонт и содержание - 1.5 тыс. ДМ;
в) один ночной дежурный - 6 тыс. ДМ;
г) один служащий для уборки территории - 8 тыс. ДМ.
Всего –25.5 тыс. ДМ.
2) Расходы, пропорциональные числу комнат отеля:
а) меблировка одной комнаты - 4 тыс. ДМ;
б) 1 горничная на 10 комнат - 6 тыс. ДМ;
в) содержание одной комнаты - 150 ДМ;
г) страхование на случай пожара для одной комнаты - 25 ДМ.
Всего на комнату – 4,775 тыс. ДМ.
3) Расходы, пропорциональные среднему числу занятых комнат:
а) стирка, уборка - 5 ДМ в день;
б) электричество, газ, вода - 5 ДМ в день.
Всего на занятую комнату – 10 ДМ в день.
Доход предпринимателя составляет 60 ДМ в день с каждой занятой комнаты.
Выбор какого проекта отеля следует считать оптимальным?
Решение. Прибыль (точнее, средняя прибыль) предпринимателя
определяется здесь двумя параметрами: х - общее число комнат отеля и у среднее число заявок на комнату в год (т.е. среднегодовой спрос). При этом
мы предполагаем, что х принимает значения 20, 30, 40, 50, а у - любое целое
значение, не превосходящее 50. Общий расход за год составляет (4775 х
+3650 у +25500) ДМ, а доход 21900 у ДМ. Прибыль за год F(x,y) = =18250 y’ 4775 х -25500 (ДМ). Здесь y'= min {y,x}. Данная задача является задачей
принятия решения в условиях неопределенности, в которой стратегии
предпринимателя (игрока) x∈{20,30,40,50}, а состояния среды y∈{0,1,…,50}.
Функция выигрыша, указывающая выигрыш (прибыль) предпринимателя в
любой ситуации, есть F(x,y). Составим таблицу функции выигрыша, взяв для
упрощения записи отдельные значения переменной y: 10, 15, 20, 25, 30, 40,
50; получаем таблицу 2.2. Таким образом, в таблице 2.2 записана матрица
A = ( ai j ) , i = 1,..,4 , j = 1,..,7 Оценки стратегий по критериям Лапласа,
Вальда, Гурвица (при α =0.2; 0.5; 0.9) приведены в таблице 2.3 (выделены
полужирным шрифтом клетки, соответствующие наилучшему исходу по
каждому из критериев).
Таблица 2.2
х\у
20
30
40
50
10
61500
13750
-34000
-81750
15
152750
20
244000
25
244000
30
244000
40
244000
50
244000
105000
57250
100750
196250
148500
100750
287250
239750
192000
378750
331000
283250
378750
513500
465750
378750
513500
648250
Таблица 2.3
x
20
30
40
50
Критерий
Лапласа
204893
248357
252785
231107
Критерий
Вальда
61500
13750
-34000
-81750
α =0.2
207500
305750
404000
502250
Критерий Гурвица
α =0.5
152750
196250
239750
283250
α =0.9
79750
50250
20750
-8750
Из таблицы 2.3 видно, что разные критерии приводят к разным
оптимальным решениям; решение об окончательном выборе проекта отеля
может быть принято только при наличии новых содержательных
соображений (например, выбор показателя пессимизма α для критерия
Гурвица).
Далее, данная задача принятия решения в условиях неопределенности
станет задачей принятия решения в условиях риска, если предприниматель
будет обладать дополнительной информацией - знанием вероятностей
наступления тех или иных состояний среды. В нашем случае оценки этих
вероятностей могут быть определены статистическим методом, если имеется
статистика спроса на проживание в отелях такого типа в сходных условиях.
Пример 2.3.
Предприниматель имеет возможность вложить свои деньги либо в
государственные ценные бумаги(1-я стратегия), либо в акции
высокодоходного предприятия (2-я стратегия). Для упрощения задачи мы
полагаем, что деньги нельзя «класть в разные корзины». Природа
(экономика) может находиться в трех состояниях: кризис, стабильное
положение,
подъем.
Матрица
выигрыша
предпринимателя
A = ( a i j ) , i = 1,2 , j = 1,..,3 представлена в табл. 2.4.
Таблица 2.4
Объект вложения
Гос. ценные бумаги
Акции
Кризис
0
-5
Состояние природы
Стабильность
3
5
Подъем
5
13
Числа в таблице – некоторые денежные единицы. Мы исходим из
естественного предположения, что государственные бумаги в благоприятной
для экономики ситуации менее доходны, чем акции. Очевидно, по критерию
Вальда решением задачи будет покупка
государственных бумаг, по
критерию Лапласа – акций. Определим, как влияет здесь параметр α на
выбор решения по критерию Гурвица. Для этого необходимо составить
уравнение
0 ⋅ α + 5 ⋅ (1 − α ) = −5 ⋅ α + 13 ⋅ (1 − α ) .
8
8
критерий Гурвица рекомендует
Решением будет α = . При α <
13
13
акции, в других случаях – государственные бумаги. Естественно, числа в
таблице выбраны в значительной мере произвольно. Выигрыши
предпринимателя в каждой ситуации могут отличаться от тех, что приведены
в таблице. Важен порядок, в котором идут элементы каждой строки этой
таблицы (максимум - в 3-м столбце, минимум – в 1-м). Тогда общее
уравнение для поиска α , граничного в смысле выбора решения, будет таким:
a11 ⋅ α + a13 ⋅ (1 − α ) = a 21 ⋅ α + a 23 ⋅ (1 − α ).
3. АНТАГОНИСТИЧЕСКИЕ ИГРЫ
Задача принятия решения, рассматриваемая в рамках системного
подхода, содержит три основные компоненты: в ней выделены система,
управляющая подсистема и среда. Теперь мы переходим к изучению задач
принятия решения, в которых на систему воздействует не одна, а несколько
управляющих подсистем, каждая из которых имеет свои цели и возможности
действий. Такой подход к принятию решений называется теоретико-игровым,
а математические модели соответствующих взаимодействий называются
играми. Ввиду различия целей управляющих подсистем, а также
определенных ограничений на возможности обмена информацией между
ними, указанные взаимодействия носят конфликтный характер. Поэтому
всякая игра представляет собой математическую модель конфликта.
Ограничимся случаем, когда управляющих подсистем две. Если цели систем
противоположны,
конфликт
называется
антагонистическим,
а
математическая модель такого конфликта называется антагонистической
игрой..
В теоретико-игровой терминологии 1-я управляющая подсистема
называется игроком 1, 2-я управляющая подсистема - игроком 2, множества
их альтернативных действий называются множествами стратегий этих
игроков. Пусть Х - множество стратегий игрока 1, Y - множество стратегий
игрока 2. Состояние системы однозначно определяется выбором
управляющих воздействий подсистемами 1 и 2, то есть выбором стратегий
x∈X и y∈Y. Пусть F(x,y)- оценка полезности для игрока 1 того состояния
системы, в которое она переходит при выборе игроком 1 стратегии х и
игроком 2 стратегии у. Число F(x,y) называется выигрышем игрока 1 в
ситуации (x,y), а функция F - функцией выигрыша игрока 1. Выигрыш игрока
1 одновременно является проигрышем игрока 2 , то есть величиной, которую
первый игрок стремится увеличить, а второй – уменьшить. Это и есть
проявление антагонистического характера конфликта: интересы игроков
полностью противоположны (то, что выигрывает один, проигрывает другой).
Антагонистическую игру естественно задать системой Г=(Х, Y, F).
Заметим, что формально антагонистическая игра задается фактически
так же, как и задача принятия решения в условиях неопределенности - если
отождествить управляющую подсистему 2 со средой. Содержательное
различие между управляющей подсистемой и средой состоит в том, что
поведение первой носит целенаправленный характер. Если при составлении
математической модели реального конфликта у нас есть основание (или
намерение) рассматривать среду как противника, цель которого - принести
нам максимальный вред, то такую ситуацию можно представить в виде
антагонистической игры. Другими словами, антагонистическую игру можно
трактовать как крайний случай ЗПР в условиях неопределенности,
характеризуемый тем, что среда рассматривается как противник, имеющий
цель. При этом мы должны ограничить виды гипотез о поведении среды.
Наиболее обоснованной здесь является гипотеза крайней осторожности,
когда, принимая решение, мы рассчитываем на самый худший для нас
возможный вариант действий среды.
Определение. Если Х и Y конечны, то антагонистическая игра
называется матричной. В матричной игре можно считать, что X={1,…,n},
Y={1,…,m} и положить aij=F(i,j). Таким образом, матричная игра полностью
определяется матрицей A=(aij), i=1,…,n, j=1,…,m.
Пример 3.1. Игра с двумя пальцами.
Два человека одновременно показывают один или два пальца и
называют число 1 или 2, означающее, по мнению говорящего, количество
пальцев, показанное другим. После того, как пальцы показаны и числа
названы, происходит распределение выигрыша по следующим правилам:
если оба угадали или оба не угадали, сколько пальцев показал их соперник,
выигрыш каждого равен нулю; если угадал только один, то противник платит
угадавшему сумму денег, пропорциональную общему числу показанных
пальцев.
Это антагонистическая матричная игра. Каждый игрок имеет четыре
стратегии: 1- показать 1 палец и назвать 1, 2- показать 1 палец и назвать 2, 3показать 2 пальца и назвать 1, 4 - показать 2 пальца и назвать 2. Тогда
матрица выигрышей A=(aij), i=1,…,4, j=1,…,4 определяется следующим
образом:
a12=2, a21 = –2, a13=a42= –3, a24=a31=3, a34 = –4, a43=4,aij=0 в остальных
случаях.
Пример 3.2. Дискретная игра типа дуэли.
Задачами дуэльного типа описывается, например, борьба двух игроков,
каждый из которых желает совершить некое единовременное действие
(выброс на рынок партии товара, заявка о покупке на аукционе) и выбирает
для этого время. Пусть игроки продвигаются навстречу друг другу на n
шагов. После каждого сделанного шага игрок может выстрелить или не
выстрелить в противника. Выстрел может быть у каждого только один.
Считается, что вероятность попасть в противника, если продвинуться на k
k
шагов, равна . Стратегия игрока 1(2) заключается в принятии решения
n
стрелять на i-м (j-м) шаге. Пусть i<j , 1-й игрок стреляет на i-м шаге, а игрок
2- на j-м шаге. Тогда выигрыш a ij игрока 1 задается формулой
i
i j n(i − j ) + ij
− (1 − ) =
.
n
n n
n2
Таким образом, выигрыш – это разность вероятностей поражения
противника и собственного выживания в дуэли. В случае i>j первым стреляет
игрок 2 и a ij = −a ji . Если i = j, то полагаем a ij = 0. Игровая матрица,
умноженная для удобства на 5, при n=5 имеет вид
a ij =
⎛ 0 − 3 − 7 − 11 − 15 ⎞
⎟
⎜
1
−2 −5 ⎟
⎜3 0
⎜ 7 −1 0
7
5 ⎟.
⎟
⎜
15 ⎟
⎜ 11 2 − 7 0
⎜15 5 − 5 15
0 ⎟⎠
⎝
Матричным играм целиком посвящены 4-я и 5-я глава пособия.
Далее в тексте множества стратегий игроков Х и Y считаются
ограниченными и замкнутыми, а функция F(x,y) - непрерывной.
Определение. Результатом, гарантированным игроку 1 при
использовании им стратегии х, называется число min F ( x, y ) . Результатом,
y ∈Y
гарантированным игроку 2 при использовании им стратегии у, называется
число max F ( x, y ) .
x∈ X
Определение. Нижней ценой игры Г=(Х, Y, F) называется величина
υ = max min F ( x, y ) . Верхней ценой игры Г называется величина
x ∈ X y ∈Y
υ = min max F ( x, y ) .
y ∈Y x ∈ X
Игрок 1 может гарантировать себе выигрыш, не меньший, чем υ , а
его противник может гарантировать себе проигрыш, не превышающий υ . В
примере 3.1 υ = -2, υ =2. Следующая теорема поясняет происхождение
названий "нижняя цена игры" и "верхняя цена игры".
ТЕОРЕМА 3.1. Для любой непрерывной функции F(x,y), определенной
на декартовом произведении компактов Х и Y, справедливо неравенство
υ ≤ υ , т.е.
(3.1)
max min F ( x, y ) ≤ min max F ( x, y ) .
y ∈Y x ∈ X
x ∈ X y ∈Y
Доказательство. Предварительно сформулируем следующую
очевидную лемму:
ЛЕММА 3.1. Если Z - компактное множество, H(z) - непрерывная
функция, то справедливы соотношения
∀z ∈ Z H ( z ) ≤ a ↔ max H ( z ) ≤ a ;
(3.2)
z∈Z
∀z ∈ Z H ( z ) ≥ a ↔ min H ( z ) ≥ a .
(3.3)
z∈Z
Очевидно, что при всех х и у min F ( x, y ′) ≤ F ( x, y ) ≤ max F ( x ′, y ).
y′ ∈Y
x′ ∈ X
Применив к этому неравенству лемму 3.1, получим требуемое
соотношение (3.1).
Определение. Если в игре Г верхняя и нижняя цены совпадают, то
говорят, что в этой игре выполнено соотношение минимакса. Число υ = υ = υ
называют ценой игры.
Определение. Пара стратегий (х0, у0) называется седловой точкой игры
Г, если выполняется соотношение
(3.4)
∀x , y F ( x , y 0 ) ≤ F ( x 0 , y 0 ) ≤ F ( x 0 , y ).
Смысл седловой точки состоит в том, что любой игрок, односторонне
отступивший от нее, не выигрывает. Например, одностороннее отступление
игрока 1 от седловой точки означает, что он выбрал не х0, а другую
стратегию x, в то время как 2-й по-прежнему придерживается стратегии у0 .
Если (i0, j0) - седловая точка в матричной игре, то элемент a
i0 j 0
минимальный в i0-й строке и максимальный в j0-м столбце матрицы.
ТЕОРЕМА 3.2. В антагонистической игре Г=(Х, Y, F) седловая точка
(х0, у0) существует тогда и только тогда, когда выполнено соотношение
минимакса
(3.5)
max min F ( x, y ) = min max F ( x, y ) .
y ∈Y x ∈ X
x ∈ X y ∈Y
При этом цена игры равна значению функции выигрыша в седловой точке, то
есть υ = F ( x 0 , y 0 ) .
Доказательство.
Необходимость. Пусть (х0, у0) - седловая точка, то есть справедливо (3.4). С
учетом соотношений (3.2) и (3.3) это условие можно переписать в виде
max F ( x, y 0 ) ≤ F ( x 0 , y 0 ) ≤ min F ( x 0 , y ). Но верны неравенства
y ∈Y
x∈ X
min max F ( x, y ) ≤ max F ( x, y 0 ),
y ∈Y x ∈ X
x∈X
min F ( x 0 , y ) ≤ max min F ( x, y ).
y ∈Y
x ∈ X y ∈Y
Получаем неравенство min max F ( x, y ) ≤ max min F ( x, y ), которое вместе
y ∈Y x ∈ X
x ∈ X y ∈Y
с (3.1) дает требуемое равенство.
Достаточность. Пусть справедливо (3.5). Выберем точки х0 и у0 так, чтобы
они удовлетворяли условиям
min F ( x 0 , y ) = max min F ( x, y ),
y ∈Y
x ∈ X y ∈Y
max F ( x, y 0 ) = min max F ( x, y ).
y ∈Y x ∈ X
x∈ X
Справедливы неравенства min F ( x 0 , y ) ≤ F ( x 0 , y 0 ) ≤ max F ( x, y 0 ).
y ∈Y
x∈ X
Из
способа
выбора
х0
и
у0
вытекает,
что
max F ( x, y 0 ) = F ( x 0 , y 0 ) = min F ( x 0 , y ). Используя (3.2) и (3.3), получаем
y ∈Y
x∈ X
(3.4), что и требовалось доказать.
Определение. Если (х0, у0) - седловая точка, то стратегия х0 называется
оптимальной для игрока 1, а стратегия у0 – оптимальной для игрока 2.
Непосредственный поиск седловых точек чаще всего проводится с помощью
проверки истинности равенства (3.5).
Пример 3.3.
Игрок 1 выбирает число х из множества Х = [0; 1], игрок 2 выбирает
число y из множества Y = [0; 1]. После этого игрок 2 платит игроку 1 сумму
F(x, y) = 2 x 2 − y 2 .
Поскольку игрок 2 хочет минимизировать выигрыш игрока 1, то он
определяет min (2x2 − y2) = 2х2 −1,т.е. при этом y = 1. Игрок 1 желает
y∈Y
максимизировать свой выигрыш, и поэтому определяет
max ( min F(x, y)) = max (2х2 -1 ) = 2−1 = 1, который достигается при х =
x∈X y∈Y
x∈X
1. Итак, нижняя цена игры равна v = 1.
Верхняя цена игры v = min ( max (2х2 − y2)) = min (2 − y2) = 2−1 = 1, то
y∈Y x∈X
y∈Y
есть в этой игре v = v = 1. Поэтому цена игры v = 1, а седловая точка - (1;1).
Пример 3.4.
1
ψ(y)
0.25
0
(1-y)2
y2
0.5
Рис. 3.1
1
X = [0;1] ; Y = [0;1] ; F ( x, y ) = ( x − y ) 2 .
Найдем
ψ ( y ) = max F ( x , y ) ,
x∈ X
.
ϕ ( x ) = min F ( x , y )
y ∈Y
Очевидно, ϕ ( x) = 0 (для любого x
достигается при y = x ). На рис. 3.1.
приведен график функции
Y
⎧⎪ y 2 , y ∈ [0.5;1]
ψ ( y) = ⎨
⎪⎩(1 − y ) 2 , y ∈ [0;0.5]
2
min ψ ( y ) = (0.5) = 0.25 . Этот минимум достигается в точке х=0.5, т.е.
y ∈Y
в той точке отрезка [0;1], где значения функций y 2 и (1 − y ) 2 совпадают.
Получаем: min max F ( x, y ) = 0.25; max min F ( x, y ) = 0.
y ∈Y x ∈ X
x ∈ X y ∈Y
Соотношение минимакса не выполнено, следовательно, седловой точки
нет.
Пример 3.5. Непрерывная дуэль.
Игроки движутся навстречу друг другу с постоянной скоростью. В
момент t=0 игроки достаточно далеко друг от друга, а при t=1 они сходятся
вплотную. На отрезке [0;1] задана вещественная функция a i (t ) - мера
меткости i-го игрока, i=1,2. Значение a i (t ) - вероятность того, что i-й игрок,
стреляя в момент t, поразит противника. Предполагается, что обе функции не
убывают, непрерывны и удовлетворяют краевым условиям a i (0 ) = 0; a i (1) = 1.
1-й игрок получает очки в количестве +1, если он поражает 2-го до
того, как сам будет поражен; -1 в симметричном случае; и 0, если ни один не
поражен, либо оба поражены одновременно.
Множества стратегий таковы:X=Y=[0;1]. Стратегия x игрока 1 означает:
«Я буду стрелять в момент t= x,если противник не выстрелит раньше. Если
же он выстрелит, но промахнется, я для надежности буду стрелять в момент
t=1». Аналогичны рассуждения второго. В качестве функции выигрыша
берем математическое ожидание суммы, начисленной 1-му игроку, то есть
⎧2a1 ( x ) − 1, x < y
⎪
F ( x, y ) = ⎨a1 ( x ) − a 2 ( x ), x = y
⎪1 − 2a ( y ), x > y.
2
⎩
Можно доказать, что множеством седловых точек 1-го игрока будет
отрезок
(возможно,
и
точка)
I,
определяемый
из
условия
I = {x1 ∈ [0,1] | 2a1 ( x ) − 1 = 1 − 2a 2 ( x )}. Такой же отрезок (точка) составит
множество седловых точек 2-го игрока. Общее значение функций 2a1 − 1 и
1 − 2a 2 на I будет ценой игры.
ТЕОРЕМА 3.3. В антагонистической игре все седловые точки
эквивалентны, а оптимальные стратегии взаимозаменяемы, то есть если (х1,
у1) и (х2, у2) - седловые точки, то (х1, у2) и (х2, у1) - также седловые точки,
причем
(3.6)
F ( x1 , y1 ) = F ( x 2 , y 2 ) = F ( x1 , y 2 ) = F ( x 2 , y1 ) .
Доказательство. Поскольку (х1, у1) и (х2, у2) - седловые точки, то
справедливы соотношения
(3.7)
∀x , y F ( x , y1 ) ≤ F ( x1 , y1 ) ≤ F ( x1 , y ).
(3.8)
∀x , y F ( x , y 2 ) ≤ F ( x 2 , y 2 ) ≤ F ( x 2 , y ).
Из них легко получить цепочки неравенств
F ( x 2 , y 2 ) ≤ F ( x 2 , y1 ) ≤ F ( x1 , y1 ),
F ( x1 , y1 ) ≤ F ( x1 , y 2 ) ≤ F ( x 2 , y 2 ),
которые влекут за собой систему равенств (3.6).
Для доказательства того, что (х1, у2) и (х2, у1) также седловые точки, нужно
доказать выполнение cледующих условий:
∀x, y
F ( x, y 2 ) ≤ F ( x1 , y 2 ) ≤ F ( x1 , y ),
∀x, y F ( x, y1 ) ≤ F ( x 2 , y1 ) ≤ F ( x 2 , y ).
Но эти условия с учетом (3.6) вытекают из (3.7) и (3.8).
ТЕОРЕМА 3.4. Если множества Х и Y ограничены, замкнуты и
выпуклы, а функция F(x,y)
непрерывна, вогнута по х при каждом
фиксированном у и выпукла по у при каждом фиксированном х, то в
антагонистической игре Г=(Х, Y, F) существует седловая точка.
Эту теорему примем без доказательства.
Игры с выпуклыми непрерывными функциями выигрыша называются
выпуклыми. Это важный класс игр, рассмотрим некоторые его свойства.
ТЕОРЕМА 3.5.Пусть F(х, y) – непрерывная функция, заданная на
единичном квадрате, строго выпуклая по y для любого х. Тогда имеется
единственная оптимальная стратегия y = yo ∈[0;1] для игрока 2, значение yo
определяется как решение уравнения max F(x,yo) = v . Аналогично и для
x
игрока 1: если функция F(х,y) непрерывна по обоим аргументам и строго
вогнута по х при любом y, то в этом случае игрок 1 имеет единственную
оптимальную стратегию хо, определяемую из уравнения
min F(x0,y) = v .
y
Замечание. Если предполагать нестрогую выпуклость функции F(х,y)
по y, то утверждения теоремы остаются в силе с той лишь разницей, что у
игрока 2 оптимальная стратегия не будет единственной. Если предполагать
нестрогую вогнутость функции F(х, y) по x, то утверждения теоремы
остаются в силе с той лишь разницей, что у игрока 1 оптимальная стратегия
не будет единственной.
Эту теорему также примем без доказательства.
Пример 3.6.
2
π ( x + y)
∂ 2F
π ( x + y)
⎛π ⎞
X=Y=[0;1];F(х,y)= sin
. Так как
sin
=
−
<0
⎜
⎟
2
2
∂ x2
⎝2⎠
для x ∈[0; 1], y ∈(0;1), F(х,y) строго вогнута по х ∀ y ∈(0;1). Тогда цена игры
π ( x + y)
1
. При 0 ≤ х ≤
находится по формуле v = max min sin
min
2
y
0 ≤ y ≤1
x
2
π ( x + y)
πx
π ( x + y)
π ( x + 1)
sin
= sin
, иначе min sin
= sin
. Поэтому в
0 ≤ y ≤1
2
2
2
2
результате следующих вычислений получаем:
π ( x + y)
π ( x + y)
v = max { max min sin
, max min sin
}=
1
1 0 ≤ y ≤1
0 ≤ y ≤1
2
2
≤x ≤1
0≤ x ≤
2
2
= max { max sin
0≤ x ≤
1
2
πx
2
, max sin
1
≤x ≤1
2
π ( x + 1)
2
} = max {
2 2
2
;
}=
.
2 2
2
Значение
х, на котором достигается максимум, равно
π ( x + y)
1
. Это же
2
2
, т.к. минимум
0 ≤ y ≤1
2
2
достигается при y = 0, и это уравнение превращается в следующее:
πx
1
2
=
, откуда следует, что х = .
sin
2
2
2
Заметим, что если в функции выигрыша поменять местами х и y, то
она не изменится, следовательно, эта функция выпукла и по y при всех х
∈[0;1]. Поэтому у игрока 2 существует оптимальная стратегия yo,
определяемая из уравнения
π ( x + y)
2
max sin
=
.
0≤x ≤1
2
2
1
Очевидно, максимум по х достигается при х = , и последнее
2
⎛1
⎞
π⎜ + y⎟
2
⎝2
⎠
=
.
уравнение примет вид sin
2
2
Решением последнего уравнения будет yo = 0. Следовательно, игрок 2
имеет оптимальную стратегию yo = 0.
значение будет решением уравнения min sin
=
4. ТЕОРИЯ МАТРИЧНЫХ ИГР
В 3-й главе уже упоминались матричные игры – один из наиболее
важных типов антагонистических игр. Теория матричных игр разработана
более подробно по сравнению с общей теорией антагонистических игр.
Известны различные алгоритмы поиска оптимальных стратегий игроков в
матричной игре, они в большинстве своём наглядны и просты в применении,
выбор алгоритма зачастую определяется размерностью матрицы.
Рассмотрим примеры поиска седловой точки в матричной игре. Поиск
проводится так: проверяется истинность соотношения минимакса, если оно
выполняется, то седловые точки – это все пары стратегий 1-го и 2-го игроков
(каждой паре соответствуют номер строки и номер столбца), выигрыш при
которых равен цене игры, а также минимален среди выигрышей - элементов
строки и максимален среди выигрышей - элементов столбца. Если же
соотношение минимакса не выполнено, то седловых точек нет.
Пример 4.1.
min aij
j
⎛1 − 3 − 2⎞
⎟
⎜
A = ⎜0
5
4⎟
⎜2
3
2 ⎟⎠
⎝
max aij = 2 5 4
14243
i
min max aij = 2
j
− 3⎫
⎪
0 ⎬ max min aij = 2
j
i
2 ⎪⎭
i
Седловой точкой является пара (3,1), при которой υ = v = v = 2.
Заметим, что хотя выигрыш в точке (3,3) также равен 2 = v = v , она не
является седловой точкой, т.к. этот выигрыш не является максимальным
среди выигрышей третьего столбца.
Пример 4.2.
min aij
⎛ 10 30 ⎞
⎟⎟
A = ⎜⎜
40
20
⎠
⎝
max aij ↓ ↓
j
→
→
10 ⎫
⎬ max min a ij = 20
j
20⎭ i
i
40 30
123
min max aij =30
j
i
Из матрицы выигрышей видно, что v < v , т.е. данная матрица не имеет
седловой точки. Если игрок 1 выбирает свою максиминную (ту, что
гарантирует ему выигрыш в размере нижней цены игры) стратегию i = 2, то
игрок 2, выбрав свою минимаксную (ту, что гарантирует ему проигрыш в
размере не большем, чем верхняя цены игры) стратегию j = 2, проиграет
только 20. В этом случае игроку 1 выгодно выбрать стратегию i = 1, т.е.
отклониться от своей максиминной стратегии и выиграть 30. Тогда игроку 2
будет выгодно выбрать стратегию j = 1, т.е. отклониться от своей
минимаксной стратегии и проиграть 10. В свою очередь игрок 1 должен
выбрать свою 2-ю стратегию, чтобы выиграть 40, а игрок 2 ответит выбором
2-й стратегии.
Пример 4.3.
Рассмотрим игровую матрицу, в которой один из элементов (а именно,
a33) неизвестен. Обозначим этот элемент x. Установим, при каких значениях x
в матрице есть седловые точки.
min aij
j
1
⎛1 5 4⎞
⎫
⎜
⎟
⎪
A = ⎜3 2 0⎟
0 ⎬ max min a ij = max[1, min{5, x}] .
j
i
⎜5 6 x⎟
min{5, x}⎪⎭
⎝
⎠
max a ij = 3 6 max(4, x)
14442444
3
i
min max a ij = 3
j
i
Таким образом, матрица имеет седловую точку при x=3. Это точка
(3,3). Других седловых точек в матрице нет. Выигрыш в точке (2,1) также
равен 3, но она не является седловой точкой, т.к. этот выигрыш не является
максимальным среди выигрышей первого столбца.
Можно легко найти и другие матрицы, не имеющие седловых точек (в
частности, из примеров 3.1 и 3.2). Более того, можно утверждать, что и в
реальной ситуации матрица, которой задается игра, чаще всего не имеет
седловых точек. Таким образом, игроки не имеют оптимальных стратегий,
им нужно искать новые критерии выбора.
Первый игрок всегда может обеспечить себе выигрыш
υ = max
max a ij , но в
min a ij , а второй - выигрыш υ = min
1 ≤ j ≤ m1 ≤ i ≤ n
1 ≤ i ≤ n1 ≤ j ≤ m
общем случае υ < υ и, следовательно, создается неустойчивая ситуация,
которую один из игроков может изменить с выгодой для себя. Значит,
игрокам следует искать дополнительные стратегические возможности для
того, чтобы гарантировать себе больший выигрыш и меньший проигрыш
соответственно. Можно более широко понимать стратегию как объект: не
только как действие, но в общем случае еще и как правило, по которому
выбирается действие. Таким образом, выбор игроков значительно
расширяется. Один из возможных путей - выбирать свои стратегии случайно,
то есть задать распределение вероятностей на множестве своих стратегий, а
после этого предоставить выбор конкретной стратегии соответствующему
случайному механизму.
Итак, выбор игроком своей стратегии с заранее заданной вероятностью
является одним из способов действия, то есть в определенном смысле тоже
стратегией. Для отличия стратегий такого вида от первоначально заданных
стратегий их называют смешанными стратегиями, а первоначально заданные
(то есть строки или столбцы матрицы) - чистыми стратегиями. Переход к
смешанным стратегиям позволяет получить большинство важных
результатов, относящихся к матричным играм. Более того, можно сказать,
что только этот переход позволяет полностью решить игру.
Определение. Смешанной стратегией игрока 1 в матричной игре
называется распределение вероятностей на множестве его чистых стратегий,
то есть любой вектор x = ( x1 ,..., x n ) , обладающий свойствами:
(4.1)
x i ≥ 0, i = 1,..., n;
n
∑ xi
= 1.
(4.2)
i =1
Смешанной стратегией игрока 2 в матричной игре называется распределение
вероятностей на множестве его чистых стратегий, то есть любой вектор
y = ( y1 ,..., y n ), обладающий свойствами
y j ≥ 0, j = 1,..., m;
(4.3)
m
∑yj
= 1.
(4.4)
j =1
Число x i , i = 1,..., n, представляет собой вероятность выбора i-й чистой
стратегии игроком 1, а y j , j = 1,..., m - вероятность выбора j-й чистой
стратегии игроком 2. i-й чистой стратегии игрока 1 соответствует смешанная
стратегия
(4.5)
ei = (0,..., 1,...,0),
i
а j-й чистой стратегии игрока 2 - смешанная стратегия
f j = (0,..., 1 ,...,0).
(4.6)
j
Таким образом, множество смешанных стратегий бесконечно.
Применение смешанных стратегий превращает процесс игры в некоторое
случайное испытание, исходами которого являются ситуации игры, то есть
пары (i,j). Это случайное испытание называется ситуацией в смешанных
стратегиях и обозначается через ( x, y). Отсутствие обмена информацией
между игроками в антагонистической игре делает случайные принятия ими
решения о своих стратегиях i и j независимыми. Поэтому каждая ситуация
(i,j) реализуется с вероятностью хi yj. Поскольку в этой ситуации игрок 1
получает выигрыш aij, математическое ожидание его выигрыша равно
n
m
F ( x, y ) = ∑ ∑ a ij x i y j .
(4.7)
i =1 j =1
Определение. Матричной игрой (со смешанными стратегиями)
называется тройка Г=(Х, Y, F), где Х - множество векторов,
удовлетворяющих условиям (4.1), (4.2), Y - множество векторов,
удовлетворяющих условиям (4.3), (4.4),
F ( x, y) - функция, заданная
формулой (4.7).
В дальнейшем под матричной игрой понимается объект, заданный
именно таким определением.
ТЕОРЕМА 4.1(основная теорема теории матричных игр). Любая
матричная игра имеет седловую точку в смешанных стратегиях.
Доказательство. Покажем, что в данном случае выполнены все
условия теоремы 3.4.
Ограниченность Х и Y вытекает из условий (4.1)-(4.4). Докажем
замкнутость и выпуклость этих множеств. Доказательство проведем для Х,
для Y оно аналогично.
′
k
k
Покажем замкнутость Х. Пусть x ∈ X при всех k , x = lim x .
k →∞
′
Докажем, что и x ∈ X . В самом деле, xik ≥ 0 при всех k и i=1,…,n,
следовательно, lim x k ≥ 0 при всех i=1,…,n, то есть x ′ ≥ 0 при всех
i
i
k →∞
n k
n k
i=1,…,n. Далее, поскольку ∑ x = 1 при всех k, то и lim ∑ x = 1 , то
i
k → ∞i =1 i
i =1
n
′
′
есть ∑ x = 1 . Таким образом, x ∈ X удовлетворяет условиям (4.1), (4.2)
i
i =1
и принадлежит Х. Итак, Х является замкнутым.
1
2
Покажем выпуклость Х. Пусть x ∈ X , x ∈ X и 0 ≤ λ ≤ 1. Так как
∀ i = 1,..., n x1i ≥ 0, xi2 ≥ 0, получаем: ∀i = 1,..., n λx1i + (1 − λ ) xi2 ≥ 0.
n
n
А условия ∑ x1i = 1 и ∑ xi2 = 1 влекут за собой соотношение:
i =1
i =1
N
∑ (λx1i + (1 − λ ) xi2 ) = 1.
I =1
Следовательно, λ x
1
2
+ (1 − λ ) x обладает свойствами (4.1), (4.2) и
принадлежит Х. Таким образом, Х является выпуклым.
Непрерывность функции F ( x, y ) , вогнутость по x и выпуклость по y
вытекает из ее линейности.
Таким образом, матричная игра Г=(Х, Y, F) удовлетворяет всем
условиям теоремы 3.4.
Следовательно, в ней существует седловая точка, что и требовалось
доказать.
ЛЕММА 4.1. Справедливы равенства
m
F (ei , y ) = ∑ aij y j ;
j =1
n
F ( x, f j ) = ∑ aij xi ;
i =1
(4.8)
(4.9)
n
m
F ( x, y ) = ∑ xi F (ei , y ) = ∑ y j F ( x, f j ).
(4.10)
i =1
j =1
Утверждение леммы вытекает непосредственно из соотношений (4.7),
(4.5) и (4.6).
Замечание.
Если x 0 , y 0 - оптимальные стратегии, υ - цена игры, то верны
равенства
(4.11)
min F ( x 0 , y ) = max min F ( x, y ) = υ ;
y
x y
max F ( x, y 0 ) = min max F ( x, y ) = υ ;
y x
x
(4.12)
(4.13)
F ( x0 , y 0 ) = υ.
В следующей серии теорем (с номерами 4.2–4.7) выражены основные
свойства оптимальных стратегий матричной игры.
ТЕОРЕМА 4.2. Пусть υ - цена игры. Для того, чтобы x 0 была
оптимальной стратегией игрока 1, необходимо и достаточно, чтобы
выполнялось условие
∀ y F ( x0 , y) ≥ υ.
(4.14)
Для того, чтобы y 0 была оптимальной стратегией игрока 2, необходимо и
достаточно, чтобы выполнялось условие
(4.15)
∀ x F ( x, y 0 ) ≤ υ .
Доказательство.
Необходимость. Если x 0 и y 0 - оптимальные стратегии, то ( x 0 , y 0 ) –
седловая точка, т.е. справедливо соотношение (3.4), из которого с учетом
(4.13) вытекает выполнение условий (4.14) и (4.15).
Достаточность. Пусть υ - цена игры и при всех y F ( x 0 , y ) ≥ υ . Пусть ( x ′ ,
y ′ ) – седловая точка, т.е. верно условие
∀ x, y
F ( x, y ′) ≤ F ( x ′, y ′) ≤ F ( x ′, y ).
(4.16)
Покажем, что ( x 0 , y ′ ) – также седловая точка. Из (4.14) и (4.16) имеем
F ( x 0 , y ′) ≥ υ , F ( x 0 , y ′) ≤ F ( x ′, y ′) = υ .Тогда F ( x 0 , y ′) = υ . Но тогда из (4.14)
вытекает соотношение ∀ y F ( x 0 , y ) ≥ F ( x 0 , y ′) , а из (4.16) – соотношение
∀ x F ( x, y ′) ≤ F ( x 0 , y ′) . Эти соотношения в совокупности означают, что ( x 0 ,
y ′ ) – седловая точка и, следовательно, x 0 - оптимальная стратегия первого
игрока. То, что y 0 - оптимальная стратегия второго игрока, доказывается
аналогично.
ТЕОРЕМА 4.3. Множество оптимальных стратегий каждого игрока
ограничено, замкнуто и выпукло.
Доказательство. Пусть Х0 – множество оптимальных стратегий
игрока 1, Y0 –множество оптимальных стратегий игрока 2. Доказательство
проведем для Х0.
Ограниченность Х0 вытекает из ограниченности множества Х и
включения Х0⊂ Х.
Для доказательства замкнутости Х0 достаточно показать, что для любой
последовательности стратегий на Х0 предел этой последовательности также
k
k
содержится в Х0. Пусть x ∈ X 0 при всех k ,
lim x = x 0 . По теореме
k →∞
k
4.2 F ( x , y ) ≥ υ при всех k и у. Переходя в этом неравенстве к пределу при
k → ∞ , с учетом непрерывности F ( x, y ) получаем справедливость для x 0
соотношения (4.14). Таким образом, данная стратегия оптимальна.
1
2
Докажем выпуклость Х0. Пусть x и x принадлежат Х0, то есть
выполнены условия: ∀ y F ( x1 , y ) ≥ υ , ∀ y F ( x 2 , y ) ≥ υ . Но тогда для
и
произвольного
имеем
любого
0 ≤ λ ≤1
y
1
2
1
2
F (λ x + (1 − λ ) x ) = λF ( x , y ) + (1 − λ ) F ( x , y ) ≥ υ . Таким образом,
1
2
удовлетворяет условию (4.14) и, следовательно,
λ x + (1 − λ ) x
принадлежит Х0. Теорема полностью доказана.
ТЕОРЕМА 4.4. Пусть υ – цена игры. Для того, чтобы x 0 была
оптимальной стратегией игрока 1, необходимо и достаточно, чтобы
выполнялось условие
∀j = 1,..., m F ( x 0 , f j ) ≥ υ .
(4.17)
Для того, чтобы y 0 была оптимальной стратегией игрока 2, необходимо и
достаточно, чтобы выполнялось условие
(4.18)
∀i = 1,..., n F (ei , y 0 ) ≤ υ .
Доказательство. Необходимость условий (4.17) и (4.18) вытекает
непосредственно из теоремы 4.2. Доказательство достаточности проведем
для x 0 . Пусть для x 0 справедливо (4.17). Используя (4.10) и (4.17), для
m
m
любого y имеем: F ( x 0 , y ) = ∑ y j F ( x 0 , f j ) ≥ ∑ y jυ = υ . Таким образом,
j =1
j =1
для x 0 справедливо условие (4.14) и, следовательно, x 0 будет оптимальной
для первого игрока.
ТЕОРЕМА 4.5.
Для любого фиксированного y справедливо равенство
(4.19)
max F ( x, y ) = max F (ei , y ).
1≤ i ≤ n
x
Для любого фиксированного x справедливо равенство
(4.20)
min F ( x, y ) = min F ( x, f j ).
1≤ j ≤ m
y
Таким образом, соответствующие максимумы и минимумы достигаются на
чистых стратегиях.
Доказательство. Фиксируем некоторую стратегию x . Неравенство
Докажем
противоположное
min F ( x, y ) ≤ min F ( x, f j ) очевидно.
1≤ j ≤ m
y
неравенство.
F ( x, y ) =
Для
любого
m
∑ y k F ( x, f k ) ≥
k =1
m
min
1≤ j ≤ m
имеем
y
F ( x, f j ) ∑ y k =
k =1
min F ( x, f j ) .
1≤ j ≤ m
Следовательно, min F ( x, y ) ≥ min F ( x, f j ) и равенство (4.20) доказано.
1≤ j ≤ m
y
Равенство (4.19) доказывается аналогично.
Следствие. Если x 0 , y 0 - оптимальные стратегии, υ – цена игры, то
верны соотношения
(4.21)
min F ( x 0 , f j ) = max min F ( x, f j ) = υ ;
1≤ j ≤ m
x 1≤ j ≤ m
max F (ei , y 0 ) = min max F (ei , y ) = υ .
1≤ i ≤ n
y 1≤ i ≤ n
ТЕОРЕМА 4.6. Пусть ( x 0 , y 0 ) –
(4.22)
седловая точка. Тогда, если для
некоторого i x0i ≠ 0 , то F (ei , y 0 ) = υ . Аналогично, если для некоторого j
y0 j ≠ 0 , то F ( x0 , f j ) = υ . Таким образом, в x 0 с положительной
вероятностью входят только те чистые стратегии, которые дают результат υ
против y 0 и в y 0 с положительной вероятностью входят только те чистые
стратегии, которые дают результат υ против x 0 .
Доказательство. Из (4.18) вытекает, что если F (ei , y 0 ) ≠ υ для
некоторого i, то F (ei , y0 ) < υ . Покажем, что неравенство F (ei , y 0 ) < υ
влечет за собой равенство x0i = 0 . В самом деле, если x0i ≠ 0 , то имеем
n
n
i =1
i =1
υ = F ( x 0 , y 0 ) = ∑ x 0 i F (e i , y 0 ) < ∑ x 0 i υ = υ .
Пришли к противоречию,
доказывающему утверждение
относительно x 0 . Для y 0 доказательство аналогично.
теоремы
Определение. Вектор a называется выпуклой комбинацией векторов
a 1 ,..., a l , если существуют такие числа λ1 ,..., λl , что λ k ≥ 0 при всех k=1,…, l.
l
∑ λk = 1 и a =
k =1
l
∑ λk a k .
k =1
Определение. Будем говорить, что вектор a = ( a1 ,..., a p ) доминирует
вектор b = (b1 ,..., b p ) , если a k ≥ bk при всех k=1,…, p. Будем говорить, что
вектор a = ( a1 ,..., a p ) строго доминирует вектор b = (b1 ,..., b p ) , если a k > bk
при всех k=1,…, p.
ТЕОРЕМА 4.7. Если в матричной игре с матрицей А=(а ij), i=1,…,n;
j=1,…,m i0-я строка строго доминируется выпуклой комбинацией других
строк, то i0-я чистая стратегия игрока 2 не входит с положительной
вероятностью ни в одну его оптимальную стратегию и, следовательно, при
решении игры i0-я строка может быть вычеркнута из матрицы. Если j0-й
столбец матрицы строго доминирует выпуклую комбинацию других
столбцов, то j0-я чистая стратегия игрока 2 не входит с положительной
вероятностью ни в одну его оптимальную стратегию и, следовательно, при
решении игры j0-й столбец может быть вычеркнут из матрицы.
Доказательство. Пусть i0-я строка матрицы строго доминируется
выпуклой комбинацией других строк, то есть существуют такие индексы
p
i1 ,..., i p и числа λi ,..., λi p , что i k ∈ {1,..., n}, λik ≥ 0, k = 1,..., p, ∑ λi = 1 и
1
k =1 k
p
a i0 j < ∑ λik a k j ∀ j=1,…,m. Положив λ i = 0 при i ∉ {i1 ,..., i p }, мы можем
k =1
последнее условие представить так:
n
∀j = 1,..., m a i j < ∑ λ i a ij .
(4.23)
i =1
n
Вектор (λ1 ,..., λ n ) удовлетворяет условиям: λi ≥ 0, i = 1,..., n, ∑ λi = 1,
i =1
то есть является смешанной стратегией игрока 1. Пусть y 0 - оптимальная
стратегия игрока 2. Исходя из (4.23),
получим
неравенства
m
m n
F ( ei 0 , y 0 ) = ∑ ai0 j y 0 j < ∑ ∑ y 0 j λi ai j = F ( λ , y 0 ) ≤ υ , и по теореме 4.6
j =1
j = 1i = 1
0
выполняется x i0 = 0 . Так как y 0 - произвольная оптимальная стратегия
игрока 2, ei0 не входит ни в какую оптимальную стратегию игрока 1.
Утверждение о строго доминирующем столбце доказываем аналогично.
Следствие. Если i0-я строка матрицы строго доминируется некоторой
другой строкой, то при решении игры она может быть вычеркнута из
матрицы. Если j0-й столбец матрицы строго доминирует некоторый другой
столбец, то при решении игры он может быть вычеркнут из матрицы.
*
Замечание. Если x = ( x1 ,..., xi0 −1 , xi0 +1 ,..., x n ) - оптимальная стратегия
игрока 1 в игре, матрица которой образована вычеркиванием из начальной
x = ( x1 ,..., xi0 −1 ,0, xi0 +1 ,..., x n ) - оптимальная
матрицы i0-й строки, то
стратегия игрока 1 в исходной игре. Аналогичное утверждение справедливо
относительно оптимальных стратегий игрока 2.
5. МЕТОДЫ РЕШЕНИЯ МАТРИЧНЫХ ИГР
Игры 2×2
Рассмотрим вначале случай, когда в матричной игре оба участника
имеют по две стратегии (игры размерности 2×2). Очевидно, такая игра
a12 ⎞
⎛a
⎟⎟. Пусть (х1, х2)- оптимальная стратегия
задается матрицей вида A = ⎜⎜ 11
a
a
⎝ 21
22 ⎠
игрока 1, (у1, у2) - оптимальная стратегии игрока 2. Тогда, исключая
тривиальный случай (наличие чистой оптимальной стратегии хотя бы у
одного из игроков), имеем:
(5.1)
x1 + x 2 = 1, x1 > 0, x 2 > 0; y1 + y 2 = 1, y1 > 0, y 2 > 0.
Из теоремы 4.6 получаем
⎧a11 x1 + a 21 x 2 = υ
(5.2)
⎨
⎩a12 x1 + a 22 x 2 = υ .
Приравнивая левые части уравнений (5.2) и подставляя x 2 = 1 − x1 ,
получаем
a − a 21
x1 = 22
, x 2 = 1 − x1 , где Δ A = (a11 + a 22 ) − ( a12 + a 21 ). (5.3)
ΔA
Аналогично находим
a − a12
y1 = 22
, y 2 = 1 − y1 , где Δ A = ( a11 + a 22 ) − ( a12 + a 21 ). (5.4)
ΔA
Цена игры υ находится подстановкой найденных значений х1, х2 в
любое из уравнений системы (5.2).
Игры 2×m
Теперь пусть матрица А матричной игры имеет размерность 2×m.
Рассмотрим графический метод решения такой игры. Базируется он на
теореме 4.5 и следствии из нее. Представим матрицу в виде
⎛ a1 ...a j ...a m ⎞
⎟.
A = ⎜⎜
⎟
b
...
b
...
b
1
j
m
⎝
⎠
Каждую смешанную стратегию первого игрока x можно задать таким
образом: x = ( x, 1 − x), 0 ≤ x ≤ 1. Оптимальная стратегия первого игрока
x 0 = ( x 0 , 1 − x 0 ) определяется из условия
min ( x a j + ( 1 − x )b j ).
min ( x 0 a j + ( 1 − x 0 )b j ) = max
1≤ j ≤ m
0 ≤ x ≤1 1≤ j ≤ m
Значение х0 удобно определять графически. Для этого введем
обозначения
ϕ j ( x) = a j x + b j (1 − x), j = 1,..., m, ϕ ( x) = min ϕ j ( x).
1≤ j ≤ m
Здесь
ϕ j ( x), j = 1,..., m
-
ϕ(x)
aj
ϕ j (x)
ϕ(x)
bj
0
x
1
x0
линейные функции, ϕ (x) вогнутая функция (ее график,
выделенный
на
рисунке
пунктиром,
называется
нижней огибающей),
х0точка, в которой достигается
максимум функции ϕ (x) .
Построив график данных
функций (рис 5.1), получим:
если х0=0 или х0=1, то для
второго
игрока
оптимальной
будет чистая
стратегия, соответствующая
ϕ j ( x), график
функции
0
ϕ j (x) j =1,...,m
которой проходит через точку
(0, ϕ (0) ) или (1, ϕ (1) ) и имеет
соответственно наибольший
ϕ(x)
отрицательный
или
Рис. 5.1
наибольший положительный
наклон среди всех прямых,
проходящих через эту точку; если максимум функции ϕ (x) достигается во
внутренней точке х0 и существует функция ϕ j ( x), график которой проходит
0
через точку ( x 0 , ϕ ( x 0 )) параллельно оси абсцисс, то оптимальной для
второго игрока является j0-я чистая стратегия; если максимум функции ϕ (x)
достигается во внутренней точке х0 и нет прямой, проходящей через точку
( x 0 , ϕ ( x 0 )) параллельно оси абсцисс, то оптимальная смешанная стратегия
второго игрока имеет вид y 0 = (0,..., y ,...,0,..., 1 − y 0 ,...,0) , график функции
0
j1
ϕ j ( x)
1
проходит
через
точку
( x 0 , ϕ ( x 0 ))
j
2
и
имеет
наибольший
положительный наклон среди всех прямых, проходящих через эту точку;
график функции ϕ j ( x)
2
проходит через точку ( x 0 , ϕ ( x 0 ))
и имеет
наибольший отрицательный наклон среди всех прямых, проходящих через
эту точку; число 0 ≤ y 0 ≤ 1 выбирается таким образом, чтобы график
функции y 0ϕ j ( x) + (1 − y 0 )ϕ j ( x) был параллелен оси абсцисс. Цена игры
1
2
подсчитывается по формуле υ = ϕ ( x 0 ) или υ = F ( x 0 , y 0 ).
Если игра имеет размерность n×2, то, например, поменяв игроков
номерами и, взяв функцию выигрыша с обратным знаком, мы снова получим
матричную игру размерности 2×n, и можем применить тот же метод.
Рассмотрим примеры нахождения решения матричной игры в
смешанных стратегиях графическим методом. Для получения подходящей
размерности матричной игры можно предварительно исключить
доминируемые стратегии.
Пример 5.1. Распределение площади посева.
У фермера имеется поле, которое он может засеять культурами А1, А2,
А3 в любой пропорции. Урожайность этих культур зависит от сочетания
погодных факторов, главными из которых являются осадки и тепло в летний
период. Будем считать, что по признаку "осадки" лето имеет три градации: Н
- нормальное, З - засушливое, Д - дождливое; по признаку "тепло" - две
градации: Н - нормальное и Ж - жаркое.
Известна урожайность культур А1, А2, А3 (в центнерах) в зависимости
от сочетания типов погодных условий (табл. 5.1), а также рыночная цена этих
культур в рублях за центнер (табл. 5.2).
Таблица 5.1
Культура
А1
А2
А3
Н,Н
133
125
80
Н,Ж
133
150
100
Осадки, тепло
З,Н
З,Ж
100
33
200
250
60
20
Д,Н
233
75
120
Д,Ж
233
100
140
Таблица 5.2
Культура
А1
А2
А3
Цена
90
120
150
Предполагается, что расходы, связанные с выращиванием культур А1,
А2, А3, одинаковы. В какой пропорции надо засеять поле культурами А1, А2,
А3, чтобы максимизировать гарантированную прибыль?
Умножая урожайность культур на их цены, получаем прибыль без
учета постоянной величины всех расходов (в табл. 5.3 прибыль записана в
тысячах рублей).
Таблица 5.3
Культура
А1
А2
А3
1
12
15
12
2
12
18
15
3
9
24
9
4
3
30
3
5
21
9
18
6
21
12
21
Таблицу 5.3 можно рассматривать как матрицу, задающую матричную
игру фермера (игрок 1) против природы (игрок 2); при этом всевозможные
стратегии природы перенумерованы по порядку. Находим решения этой
игры графическим методом (построения приведены на рис. 5.2).
Убеждаемся, что в данной игре нет седловой точки. Производим
упрощение игры, исключая доминируемые стратегии игроков. В данном
случае второй столбец матрицы доминирует первый, а шестой - пятый.
Вычеркиваем столбцы №2 и №6, после чего в новой матрице первая строка
доминирует третью. Вычеркиваем третью строку, соответствующую
доминируемой стратегии игрока 2, получаем матричную игру размерности
⎛12 9 3 21⎞
⎟⎟ .
2×4, представленную матрицей ⎜⎜
15
24
30
9
⎝
⎠
Примем за х вероятность выбора стратегии А1 и за (1-х) - вероятность
выбора стратегии А2. В декартовой системе координат (рис 5.2) строим
графики функций ϕ j ( x ).
ϕ 1 ( x ) = 12 x + 15(1 − x );
ϕ 3 (x ) = 9 x + 24(1 − x );
ϕ 4 ( x ) = 3x + 30(1 − x );
ϕ 5 ( x ) = 21x + 9(1 − x ).
По графику установим, что М* - верхняя точка нижней огибающей
данного семейства прямых соответствует пересечению графиков функций
ϕ 1 ( x ) и ϕ 5 ( x ). Тогда x 0 удовлетворяет следующему уравнению:
12x + 15(1 − x ) = 21x + 9(1 − x ). Следовательно,
x 0 = 0.4, а цена игры в
смешанных стратегиях υ = ϕ 1 ( xo ) = ϕ 5 ( x 0 ) = 13.8.
Оптимальную стратегию 2-го игрока будем искать в виде
y 0 = ( y 0 ,0,0,0, 1 − y 0 ,0). График функции y 0ϕ 1 ( x) + (1 − y 0 )ϕ 5 ( x) должен
быть параллелен оси абсцисс, то есть коэффициенты при x должны быть
равны нулю.
y 0ϕ 1 ( x) + (1 − y 0 )ϕ 5 ( x) = y 0 (15 − 3 x) + (1 − y 0 )(12 x + 9) = v.
− 3 y 0 + 12 − 12 y 0 = 0.
12
Тогда y 0 = . Перенося эти результаты в первоначальную игру,
15
находим окончательное ее решение: x0 =(0.4, 0.6, 0), y 0 =(0.8, 0, 0, 0, 0.2, 0),
υ =13.8.
Можно было бы после построения графика решить задачу другим
способом: перейти к игре размерности 2×2, оставляя из чистых стратегий
⎛12 21⎞
⎟⎟ по формулам
игрока 2 только первую и пятую. Для матрицы A = ⎜⎜
⎝15 9 ⎠
(5.2) - (5.4) находится решение.
φj(x)
30 φ4(x)
30
27
27
φ3(x)
24
24
21
21
18 φ1(x)
18
M*
15
12
φ5(x)
φ(x)
15
υ
12
9
9
6
6
x0
x
Рис. 5.2
Результат интерпретируется следующим образом: оптимальная
стратегия фермера состоит в том, чтобы 40% поля засеять культурой А1, 60%
- культурой А2, а культуру А3 не сеять совсем. При этом фермер получит
максимально возможную гарантированную прибыль в 13.8 тыс. руб. Здесь
речь идет о гарантированной прибыли, то есть о той, которая получается при
наиболее неблагоприятном сочетании погодных факторов. В случае более
благоприятного сочетания погодных условий прибыль фермера
увеличивается, см. рис. 5.2. Отметим также, что в данной задаче компоненты
смешанной стратегии игрока 1 (фермера) могут быть интерпретированы не
как вероятности использования чистых стратегий, а как доли, в которых
засевается общая площадь поля той или иной культурой. Таким образом,
смешанная стратегия игрока здесь носит характер "физической смеси",
принимая вид пропорций сочетания культур А1, А2, А3. В этом случае
оптимальная стратегия игрока максимизирует не ожидаемую, а
гарантированную прибыль.
Пример 5.2. Полицейские и воры.
В магазине работает охранная служба (в рабочее время это двое
полицейских в штатском). Торговый зал магазина делится на две условные
зоны – в зоне А почти всегда посетителей значительно больше, чем в зоне В.
Имеется некоторая позиция Т вне торговой площади, в T установлена
телекамера. В каждой из двух условных зон может находиться похититель
товаров (считаем, что он один, и далее называем его вором). Полицейские же
могут находиться в А, в В или в Т.
Предполагается, что известны
вероятности обнаружения вора в определенной зоне при условии, что
полицейский находится в фиксированном месте. Так, вора, находящегося в
А, полицейский на том же месте заметит с вероятностью 0.4; из зоны Т он
заметит его в зоне А с вероятностью 0.3; и т.д. в соответствии с матрицей
(название строки – позиция вора, название столбца – позиция охраны).
Т
А
В
⎛ 0.3 0.4 0.1 ⎞
⎜⎜
⎟⎟
В ⎝ 0.5 0.2 0.7 ⎠
Так как полицейских двое, то они могут находиться вместе или в
разных местах. Всего 6 возможных ситуаций взаимного расположения
полицейских ( обозначим их AA, АВ, АТ, ВВ, ВТ, ТТ). Для каждой из
ситуаций можно подсчитать вероятность обнаружения вора в каждой зоне.
Для подсчета используем формулы вероятности суммы.
Пусть вор, например, в зоне А.
Пусть pTA , p AA , p BA - вероятности обнаружения вора (находящегося в A)
из T,A или B соответственно. В соответствии с вышеприведенной матрицей
pTA = 0.3; p AA = 0.4; p BA = 0.1.
А
A
A
A
Пусть pTT
- вероятности обнаружения вора (находящегося в
, p AT
, p AB
А) парой полицейских, находящихся в Т, в А и Т, в В и Т соответственно.
A
pTT
= pTA + pTA − pTA ⋅ pTA = 0.3 + 0.3 − 0.3 ⋅ 0.3 = 0.51 ;
A
p AT
= p AA + pTA − p AA ⋅ pTA = 0.4 + 0.3 − 0.4 ⋅ 0.3 = 0.58 ;
A
p AB
= p AA + p BA − p AA ⋅ p BA = 0.4 + 0.1 − 0.4 ⋅ 0.1 = 0.46.
Подобным образом рассчитываются остальные вероятности.
Получим матрицу (название строки – место вора, столбца - охраны).
ТТ
А ⎛ 0.51
АА
ВВ
ТА
ТВ
0.64 0.19 0.58 0.37 0.46 ⎞
⎜⎜
⎟⎟
В ⎝ 0.75 0.36 0.91 0.6 0.85 0.76 ⎠
Если рассматривать вора и охрану как первого и второго игроков,
стратегию каждого игрока – как выбор места (для воровства или для
наблюдения соответственно) и взять элементы данной матрицы с
отрицательным знаком, то мы получим матричную игру. Выигрыш охраны
(или проигрыш вора) – это вероятность обнаружения. Легко установить, что
седловой точки в матрице нет. Решение данной матричной игры находим
графическим методом, приняв за х вероятность выбора вором зоны А и за (1х) - вероятность выбора им же зоны В. В декартовой системе координат (рис.
5.3) строим графики следующих функций:
− ϕ 1 ( x) = 0.51 x + 0.75 (1 − x);−ϕ 2 ( x) = 0.64 x + 0.36 (1 − x).
− ϕ 3 ( x) = 0.19 x + 0.91 (1 − x);−ϕ 4 ( x) = 0.58 x + 0.60 (1 − x).
− ϕ 5 ( x) = 0.37 x + 0.85 (1 − x);−ϕ 6 ( x) = 0.46 x + 0.76 (1 − x).
-φ
1
-φ2(x) и -φ1(х)
-φ4(х)
0,5
-φ6(х)
-φ5(х)
-φ2(х)
-φ3(х)
0,1
0
0,1
0,5
x0
1
Рис. 5.3
Здесь для удобства построений, чтобы не переходить к отрицательным
числам, рассматриваются выигрыши второго игрока (представителей
охраны). Таким образом, сверху на графике черной ломаной (верхней
− ϕ ( x) = max (−ϕ j ( x)). Число x0 ,
огибающей) выделена функция
1≤ j ≤ 6
определяющее оптимальную стратегию первого игрока, находим как точку, в
которой достигается min ϕ ( x) . Эта точка соответствует пересечению
x ∈ [0,1]
второй и четвертой прямых, другие прямые через ( x0 ,ϕ ( x0 ) ) не проходят.
Тогда, исходя из того, что функции ϕ 2 и ϕ 4 должны быть равны, получим:
0.36+0.28x0=0.60-0.02x0.
Тогда x0=0.8, а цена игры v = ϕ ( x0 ) = −0.564 . Оптимальную стратегию
2-го игрока будем искать в виде y0 = (0, y0 ,0,1 − y0 ,0,0). График функции
y0ϕ 2 ( x) + (1 − y0 )ϕ 4 ( x) должен быть параллелен оси абсцисс, то есть
коэффициенты при x должны быть равны нулю.
y 0ϕ 2 ( x) + (1 − y 0 )ϕ 4 ( x) = y 0 (−0.36 − 0.28 x) + (1 − y 0 )(−0.60 + 0.02 x) = v.
− 0.28 y 0 + 0.02 − 0.02 y 0 = 0.
1
Тогда y0 = . Оптимальная стратегия полицейских имеет вид
15
1 14
(0, ,0, ,0,0). Таким образом, полицейские должны пятнадцатую часть
15 15
своего рабочего времени проводить вместе в A. Оставшееся же время один из
должен проводить в A, а другой в Т. Вор должен пятую часть краж
совершать в В, а местом других его преступлений будет A. Таковы
оптимальные стратегии игроков. Полицейские гарантируют себе вероятность
поимки преступника, равную 0.564, а преступник знает, что вероятность его
задержания будет не более 0.564.
Игры 3×3
Графический подход, основанный на утверждениях теоремы 4.5,
применим также к играм размерности 3хn. Рассмотрим наиболее простой
частный случай - алгоритм решения игр 3х3.
В трехмерном случае смешанные стратегии игроков задаются
следующим образом:
x = ( x1 , x 2 , x3 ); x1 + x 2 + x3 = 1; 0 ≤ xi ≤ 1.
(5.5)
(5.6)
y = ( y1 , y 2 , y 3 ); y1 + y 2 + y 3 = 1; 0 ≤ y j ≤ 1.
Введем следующие обозначения:
3
ϕ j ( x) = F ( x, f j ) = Σ a ij xi ,
i =1
3
j = 1,...,3.
ψ i ( y ) = F (ei , y ) = Σ a ij y j , i = 1,...,3.
j =1
Составляется система уравнений
⎧ϕ 1 = ϕ 2
⎪
(5.7)
⎨ϕ 1 = ϕ 3 .
⎪ϕ = ϕ
3
⎩ 2
Каждое из уравнений данной системы определяет плоскость в
3мерном пространстве. Ищутся точки пересечения этих трех плоскостей
между собой в плоскости треугольника решений (этот треугольник (рис. 5.4)
- множество точек, удовлетворяющих (5.5)), точки пересечения каждой из
трех плоскостей со сторонами треугольника, а также вершины треугольника.
Все эти точки
образуют множество X. Являясь стратегиями, они
удовлетворяют условию x1 + x2 + x3 = 1. Оптимальная стратегия x0 первого
игрока выбирается именно на этом множестве так, чтобы выполнялось:
min ϕ j ( x 0 ) = max min ϕ j ( x ) = v. Такая стратегия может быть и не
1≤ j ≤ 3
x∈ X 1≤ j ≤ 3
единственна.
Для поиска оптимальных стратегий второго игрока
система уравнений
⎧ψ 1 = ψ 2
⎪
⎨ψ 1 = ψ 3 .
⎪ψ = ψ
3
⎩ 2
составляется
(5.8)
Далее процесс решения сходен с
x3
поиском оптимальных стратегий 1-го
игрока. Каждое из уравнений данной
1
системы определяет плоскость в 3мерном пространстве. Ищутся точки
пересечения этих трех плоскостей
между
собой
в
плоскости
треугольника решений (множества
точек, удовлетворяющих (5.6) и
x2
1
представляющего собой треугольник,
аналогичный тому, что приведен на
рис. 5.4), точки пересечения каждой
1
Рис. 5.4
из трех плоскостей со сторонами x1
треугольника, а также вершины
треугольника. Все эти точки образуют множество Y. Являясь стратегиями,
элементы Y удовлетворяют условию y1 + y2 + y3 = 1. Оптимальная стратегия
y0 2-го игрока выбирается именно на этом множестве
так, чтобы
выполнялось:
max ψ i ( y 0 ) = min max ψ i ( y ) = υ .
1≤ i ≤ 3
y ∈Y 1 ≤ i ≤ 3
Такая стратегия может быть и не единственна.
Трехмерный графический метод обыкновенно применяется в том
случае, если нет седловых точек в чистых стратегиях.
Пример 5.3.
⎛1 1 2⎞
⎜
⎟
Рассмотрим игру с матрицей ⎜ 0 2 0 ⎟ .
⎜ 2 0 0⎟
⎝
⎠
Для решения игры графическим методом найдем функции ϕ j .
ϕ 1 = x1 + 2 x 3 ; ϕ 2 = x1 + 2 x 2 ; ϕ 3 = 2 x1 .
⎧ x1 + 2 x3 = x1 + 2 x2
⎪
Система уравнений (5.7) будет иметь вид ⎨ x1 + 2 x2 = 2 x1
.
⎪2 x = x + 2 x
⎩ 1
1
3
Опустим элементарные алгебраические вычисления, производимые во
время поиска точек, образующих множество Х. Все эти 7 точек приведены на
рис 5.5. Как видно из рисунка, все плоскости пересекаются в одной точке G.
⎛1 1 1⎞
Ее координаты - ⎜ , , ⎟.
G(0,0,1)
⎝2 4 4⎠
Составим матрицу значений
ϕ j x для x ∈ X , j = 1,2,3 .
()
G
D(0,1/2,1/2)
A
B
C
D
E
F
G
F(2/3,0,1/3)
A(1,0,0) B(2/3,1/3,0)
C(0,1,0)
Рис. 5.5
1
2
3
⎛ 1
⎜
⎜ 23
⎜ 0
⎜
⎜ 1
⎜ 2
⎜
⎜ 43
⎜ 1
⎝
1
4
3
2
1
0
2
3
1
2 ⎞
4 ⎟⎟
3
0 ⎟
⎟
0 ⎟
0 ⎟
⎟
4 ⎟
3
1 ⎟⎠
Получаем: у первого игрока есть две оптимальные стратегии - (1,0,0) и
(1/2,1/4,1/4) - те, в которых достигается max min ϕ j ( x) =1 (в первой и
x∈ X 1≤ j ≤ 3
седьмой строках наибольшие минимумы, равные 1). Цена игры v =1.
Найдем функции ψ i .
E(0,0,1)
D(0,2/3,1/3
F(2/3,0,1/3)
A(1,0,0)
B(1/2,1/2,0)
C(0,1,0)
Рис. 5.6
ψ 1 = y1 + y 2 + 2 y 3 ;ψ 2 = 2 y 2 ;ψ 3 = 2 y1 . .
Система уравнений (5.8) будет
⎧ y1 + y2 + 2 y3 = 2 y 2
⎪
иметь вид ⎨2 y2 = 2 y1
.
⎪2 y = y + y + 2 x
1
2
3
⎩ 1
Все 6 точек, образующих
множество Y, приведены на рисунке
5.6.
Все три плоскости
пересекаются в одной и той же точке.
Составим матрицу значений
ψ i ( y ) для y ∈ Y , i = 1,2,3 .
1
A
B
C
D
E
F
2
3
⎛ 1
⎜
⎜ 1
⎜ 1
⎜
⎜ 43
⎜ 2
⎜
⎜4
⎝ 3
0
1
2
4
3
0
0
2 ⎞
⎟
1 ⎟
0 ⎟
⎟
0 ⎟
0 ⎟
⎟
4 ⎟
3⎠
Получаем: у второго игрока есть одна оптимальная стратегия (1/2,1/2,0) - та, в которой достигается min max ψ i ( y ) = υ =1 (во второй
y 1≤ i ≤ n
строке – наименьший максимум=1).
Метод Брауна-Робинсон
Аналитическое решение матричных игр произвольной размерности
(например, сведением к задаче линейного программирования) весьма
затруднительно. Для приближенного решения матричных игр произвольной
размерности рассмотрим итеративный метод Брауна-Робинсон. Пусть дана
матричная игра с матрицей А=(aij), i=1,…,n; j=1,…,m. Рассматривается
бесконечный процесс повторения данной игры, при котором каждый из
игроков на каждом шаге предполагает, что противник выберет смешанную
стратегию, определяемую частотами появлений чистых стратегий на
предыдущих шагах, а сам выбирает чистую стратегию, обеспечивающую
наилучший результат при данном предположении. Пусть уже сделано k
повторений игры, в которых первый игрок выбирал чистые стратегии i1,…, ik,
а второй - j1,…, jk. Тогда в соответствии с вышесказанным игрок 1 выберет на
(k+1)-м шаге стратегию ik+1 из условия
1 k
1 k
=
= υ1 (k ),
∑ ai
∑ a
max
k ν = 1 k + 1 jν 1 ≤ i ≤ n k ν = 1 i jν
а игрок 2 - стратегию jk+1 из условия
1 k
1 k
= min
= υ 2 (k ).
∑ ai j
∑ a
k ν = 1 ν k + 1 1 ≤ j ≤ m k ν = 1 iν j
Если же стратегий, удовлетворяющих соответствующему условию,
несколько, игрок выбирает любую из них.
Истинный платеж на (k+1)-м шаге равен ai j
, а средний платеж k +1 k +1
1 k +1
*
∑ ai j = υ (k ). Но эта величина не учитывается в итеративном
k + 1ν = 1 ν ν
процессе. Чистые стратегии i1 и j1 выбираются произвольно.
k
k
Обозначим через x и y предполагаемые смешанные стратегии
игроков на (k+1)-м шаге. Имеем цепочку неравенств
1 k
υ1 (k ) = max
∑ ai j = max F (ei , y k ) ≥ min max F (ei , y ) =
k
1≤ i ≤ n ν =1 ν 1≤ i ≤ n
y 1≤ i ≤ n
1 k
= max min F ( x, f j ) ≥ min F ( xk , f j ) = min
∑ ai
k
1≤ j ≤ m
1≤ j ≤ m ν =1 ν
x 1≤ j ≤ m
j
= υ 2 (k ).
Дж. Робинсон доказала справедливость следующего соотношения:
lim υ1 (k ) = lim υ 2 (k ) = υ . Оно означает, что воображаемые платежи
k →∞
k →∞
υ1 (k ) и υ 2 (k ) стремятся к истинной цене игры υ .
Сходимость этого итеративного метода медленная, но значение его
велико, так как он прост и в какой-то мере отражает приобретение игроками
опыта в результате многих повторений конфликтной ситуации.
Пример 5.4.
Рассмотрим применение метода Брауна-Робинсон (5 итераций) для
⎛12 9 3 21⎞
⎟⎟ .
матрицы ⎜⎜
⎝15 24 30 9 ⎠
Такая матричная игра исследовалась графически в примере 5.1.
Предположим, на 1-м шаге оба игрока выбрали стратегии с 1-м
номером. i1 = 1; j1 = 1.
Тогда
начальные
смешанные
стратегии
игроков
таковы:
x = (1,0) ; y = ( 1,0,0,0 ) .
Пусть k =1. На (k+1)-м шаге
1 k
∑ a i j = max{12,15} = 15 = υ1 (k ) .
max
k
1≤ i ≤ n ν =1 ν
1-й игрок выберет 2-ю стратегию, i 2 = 2.
1 k
∑ ai j = min{12, 9, 3, 21} = 3 = υ 2 (k ) .
min
k
1≤ j ≤ m ν =1 ν
2-й игрок выберет 3-ю стратегию, j 2 = 3.
2
2
1 1
⎛1 1⎞
Тогда x = ⎜ , ⎟ ; y = ( ,0, ,0) .
2 2
⎝2 2⎠
Пусть k =2. На (k+1)- м шаге
12 + 3 15 + 30
45
1 k
,
}=
= υ1 ( k ) .
∑ a i j = max{
max
k
2
2
2
ν
1≤ i ≤ n ν =1
1-й игрок выберет 1-ю стратегию, i3 = 2.
1
1
1 k
12 + 15 9 + 24 3 + 30 21 + 9 27
,
,
,
}=
= υ 2 (k ) .
∑ ai j = min{
min
ν
k
2
2
2
2
2
1≤ j ≤ m ν =1
2-й игрок выберет 1-ю стратегию, j 3 = 1.
3
3
2 1
⎛1 2⎞
Тогда x = ⎜ , ⎟ ; y = ( ,0, ,0) .
3 3
⎝3 3⎠
Пусть k =3. На (k+1)-м шаге
12 ⋅ 2 + 3 15 ⋅ 2 + 30 60
1 k
,
}=
= υ1 ( k ) .
∑ a i j = max{
max
k
3
3
3
ν
1≤ i ≤ n ν =1
1-й игрок выберет 1-ю стратегию, i 4 = 2.
1 k
12 + 15 ⋅ 2 9 + 24 ⋅ 2 3 + 30 ⋅ 2 21 + 9 ⋅ 2
,
,
,
}=
∑ ai j = min{
min
ν
k
3
3
3
3
1≤ j ≤ m ν =1
39
=
= υ 2 (k ).
3
2-й игрок выберет 4-ю стратегию, j 4 = 4.
4
4
2 1 1
⎛1 3⎞
Тогда x = ⎜ , ⎟ ; y = ( ,0, , ) .
4 4 4
⎝4 4⎠
Пусть k =4. На(k+1)-м шаге
12 ⋅ 2 + 3 + 21 15 ⋅ 2 + 30 + 9 69
1 k
,
}=
= υ1 (k ) .
∑ a i j = max{
max
k
4
4
4
ν
1≤ i ≤ n ν =1
1-й игрок выберет 2-ю стратегию, i5 = 2.
1 k
12 + 15 ⋅ 3 9 + 24.3 3 + 30 ⋅ 3 21 + 9 ⋅ 3
,
,
,
}=
∑ ai j = min{
min
ν
k
4
4
4
4
1≤ j ≤ m ν =1
48
=
= 12 = υ 2 (k ).
4
2-й игрок выберет 4-ю стратегию, j 5 = 4.
5
5
2 1 2
⎛3 2⎞
Тогда x = ⎜ , ⎟ ; y = ( ,0, , ) .
5 5 5
⎝5 5⎠
Цена игры равна 13.8, как уже известно из решения, полученного в
примере 5.1. Значения υ1 (4) = 17.25 и υ 2 ( 4) = 12 достаточно сильно
разнятся. Пример показывает, что ожидать от метода Брауна-Робинсон
оценок, близких к истинным значениям, можно лишь при большом числе
итераций. Для этого требуется автоматизация процесса вычислений.
6. БИМАТРИЧНЫЕ ИГРЫ
В предыдущих главах мы исследовали антагонистические игры. Теперь
рассмотрим общий случай игр двух игроков на конечных множествах
стратегий с интересами, не являющимися противоположными (то есть
неантагонистическими): у каждого игрока имеется своя функция выигрыша,
не обязательно противоположная функции выигрыша противника.
Определение. Биматричной игрой называется система из четырех
элементов Г=(Х, Y, F, G), где X={1,…,n}, Y={1,…,m}- конечные множества
стратегий игроков 1 и 2 соответственно; F(i,j) и G(i,j) - их функции
выигрыша.
Функции выигрыша F и G можно задать матрицами А=(aij) и B=(bij)
(i=1,…,n; j=1,…,m). Смешанные стратегии игроков и функции выигрыша для
таких стратегий определяются так же, как и в матричных играх. Далее под
биматричной игрой понимается игра со смешанными стратегиями.
Определение. Пара стратегий ( x 0 , y 0 ) называется ситуацией
равновесия биматричной игры, если справедливы соотношения
∀ x F ( x , y 0 ) ≤ F ( x0 , y 0 );
(6.1)
∀ y G( x0 , y ) ≤ G( x0 , y 0 ).
(6.2)
Смысл ситуации равновесия состоит в том, что каждому игроку
невыгодно односторонне отступать от входящей в ситуацию стратегии.
Таким образом, понятие ситуации равновесия обобщает понятие седловой
точки матричной игры.
Представляет определенный интерес оптимальность в смысле,
отличном от того, который дает понятие ситуации равновесия.
Определение. Пара стратегий (x0 , y0 ) называется оптимальной по
( )
Парето, если не существует другой пары стратегий x, y , такой, что
F ( x, y 0 ) ≥ F ( x 0 , y 0 ), G ( x 0 , y ) ≥ G ( x 0 , y 0 )
(притом хотя бы одно из неравенств является строгим).
Содержательно оптимальность по Парето означает следующее: нет
другой ситуации, которая была бы строго предпочтительнее для обоих
игроков.
Формальное различие между ситуацией равновесия и ситуацией,
оптимальной по Парето, следующее: в первой ни один игрок, действуя в
одиночку, не может увеличить своего собственного выигрыша, а во второй
оба игрока, действуя совместно, не могут (даже нестрого) увеличить
выигрыш каждого. Выбор Парето-оптимальной пары стратегий может
приводить к ситуациям, более выгодным для обоих участников, чем
ситуации равновесия.
Для матричных игр ситуация равновесия и Парето-оптимальность –
равносильные понятия. Сколько-нибудь подробное изложение достаточно
важной теории Парето-оптимальности не входит в пособие.
ТЕОРЕМА 6.1. Каждая биматричная игра имеет по крайней мере одну
ситуацию равновесия.
Доказательство. Сначала построим отображение Т множества пар
стратегий в себя так, чтобы неподвижные точки отображения совпадали с
ситуациями равновесия. Положим для ( x, y )
c i = max( F (ei , y ) − F ( x, y ),0), i = 1,..., n,
d i = max(G ( x, f j ) − G ( x, y ),0),
x i' =
j = 1,..., m,
yj +dj
xi + ci
, i = 1,..., n, y 'j =
,
m
n
1 + ∑ ck
1 + ∑ dk
k =1
k =1
Т ( x , y )=( x ′, y ′ ).
Нетрудно проверить, что
x' = ( x1' ,..., x n' ) и
j = 1,..., m.
y ' = ( y1' ,..., y m' ) - смешанные
стратегии. Покажем, что Т ( x , y )=( x , y ) тогда и только тогда, когда ( x, y )ситуация равновесия.
Пусть ( x 0 , y 0 ) - ситуация равновесия. Тогда F (ei , y 0 ) ≤ F ( x 0 , y 0 ) при
всех
i=1,…,n
d j = 0 , y0' j = y0 j
и,
следовательно,
при всех
c i = 0 , x 0' i = x 0i .
Аналогично,
j=1,…,m. Таким образом, действительно,
Т ( x 0 , y 0 ) =( x 0 , y 0 ).
Предположим, что ( x 0 , y 0 ) не является ситуацией равновесия. Тогда
либо существует x , для которого F ( x, y 0 ) > F ( x 0 , y 0 ) , либо существует y ,
для которого G ( x 0 , y ) > G ( x 0 , y 0 ) . Пусть имеет место первый случай. Тогда
существует i0, для которого
F (ei0 , y 0 ) > F ( x 0 , y 0 ) . В самом деле, в
противном случае мы имеем F (ei , y 0 ) ≤ F ( x 0 , y 0 ) при всех i=1,…,n , откуда
n
n
x
F
(
e
,
y
)
≤
∑ x i F ( x 0 , y 0 ) , равносильное
∑ i
i
0
i =1
i =1
неравенству F ( x, y 0 ) ≤ F ( x 0 , y 0 ) , которое противоречит нашему исходному
n
предположению. Для данного i0 c i0 > 0 и, следовательно, ∑ c k > 0.
k =1
Теперь покажем, что существует i1, для которого F (ei , y 0 ) ≤ F ( x 0 , y 0 ).
вытекает
неравенство
1
F (ei , y 0 ) > F ( x 0 , y 0 ) при всех
i=1,…,n . Тогда справедливо
n
n
неравенство ∑ x 0i F ( ei , y 0 ) > ∑ x 0i F ( x 0 , y 0 ) , эквивалентное неравенству
i =1
i =1
F ( x 0 , y 0 ) > F ( x 0 , y 0 ).
Приходим к противоречию, доказывающему справедливость нашего
утверждения.
Пусть
Итак, F (ei1 , y 0 ) ≤ F ( x 0 , y 0 ) и, следовательно, ci1 = 0 . Но тогда
x i1
x i'1 =
≠ xi1 , x 0' ≠ x 0 и Т ( x 0 , y 0 ) ≠ ( x 0 , y 0 ) , что и требовалось
n
1 + ∑ ck
k =1
доказать.
Итак, мы построили отображение множества пар стратегий в себя,
такое, что неподвижные точки отображения совпадают с ситуациями
равновесия.
Заметим, что множество пар стратегий является ограниченным,
замкнутым и выпуклым, а построенное отображение непрерывным. Тогда
можно применить следующую теорему:
ТЕОРЕМА БРАУЭРА. Пусть S компактное
выпуклое
подмножество
k-мерного евклидового пространства; f – непрерывная
функция, отображающая S в себя. Тогда существует по крайней мере одна
такая точка s∈ S, что f(s)=S.
Итак, отображение Т имеет по крайней мере одну неподвижную
точку. Следовательно, биматричная игра имеет по крайней мере одну
ситуацию равновесия.
Доказательство теоремы 6.1 завершено.
В чистых же стратегиях ситуация равновесия существует в
биматричной игре не всегда (как в матричной игре не всегда есть седловые
точка). Рассмотрим примеры поиска чистых ситуаций равновесия.
Пример 6.1.
⎛7 5 1⎞
⎛ 3 2 5⎞
⎜
⎟
⎜
⎟
A = ⎜ 6 3 2 ⎟, B = ⎜ 0 6 7 ⎟ .
⎜ 4 0 9⎟
⎜1 6 4⎟
⎝
⎠
⎝
⎠
Позиции максимумов в столбцах матрицы А – (1,1),(1,2),(3,3). Позиции
максимумов в строках матрицы В – (1,3),(2,3),(3,2). Соответствующие
значения обведены кружками. Эти два множества позиций не пересекаются,
следовательно, ситуации равновесия в чистых стратегиях нет.
⎛8 4 6⎞
⎛ 4 4 5⎞
⎜
⎟
⎜
⎟
A = ⎜ 7 8 9 ⎟, B = ⎜ 3 7 6 ⎟ .
⎜ 2 1 3⎟
⎜ 5 6 9⎟
⎝
⎠
⎝
⎠
Позиции максимумов в столбцах матрицы А – (1,1),(2,2),(2,3). Позиции
максимумов в строках матрицы В – (1,1),(1,2),(2,2),(3,3). Пересечение этих
двух множеств – (1,1) и (2,2). Таким образом, есть две ситуации равновесия в
чистых стратегиях - (e1 , f 1 ) и ( e 2 , f 2 ) .
В антагонистических играх седловые точки являются
эквивалентными, а оптимальные стратегии взаимозаменяемыми. Приведем
примеры, показывающие, что ситуации равновесия биматричных игр в
общем случае этими свойствами не обладают.
Пример 6.2. Семейный спор.
⎛ 4 0⎞
⎛1 0⎞
⎟⎟, B = ⎜⎜
⎟⎟.
A = ⎜⎜
0
1
0
4
⎝
⎠
⎝
⎠
Интерпретация этого примера такова. "Игроки" - жена и муж. Каждый
игрок имеет две чистые стратегии: 1 - пойти в цирк и 2 - пойти в театр. Жена
предпочитает цирк, муж - театр, но каждый предпочитает совместное
времяпрепровождение раздельному. В
соответствии с этими
предпочтениями и расставлены выигрыши, представленные в балльной
шкале. В этой игре имеется две ситуации равновесия в чистых стратегиях:
Однако
они
не
являются
эквивалентными:
(e1 , f 1 ) и ( e 2 , f 2 ) .
4 = F (e1 , f1 ) ≠ F (e 2 , f 2 ) = 1, 1 = G (e1 , f1 ) ≠ G (e 2 , f 2 ) = 4. Стратегии же,
входящие в ситуации равновесия, не взаимозаменяемы: пары стратегий
(e1 , f 2 ) и ( e 2 , f 1 ) ситуациями равновесия не являются. Таким образом,
несмотря на наличие в данной игре двух ситуаций равновесия в чистых
стратегиях, "решения" (в интуитивном смысле) она не имеет и исход игры
предсказать трудно.
Известна задача о разделе ста долларов. Два игрока должны поделить
между собой эту сумму. Стратегия каждого – назвать то число долларов,
которое он хочет получить, то есть число от 0 до 100. Если два названных
числа в сумме не превышают 100, раздел состоялся. Иначе оба игрока ничего
не получают. Даже если разрешить игрокам называть только целые числа,
игра будет иметь 101 ситуацию равновесия в чистых стратегиях. Эти
ситуации представляют все возможные варианты полного раздела суммы.
Такой пример снова подчеркивает уязвимость ситуации равновесия как
решения игры.
Даже в том случае, когда в биматричной игре имеется
единственная ситуация равновесия, ее зачастую трудно считать решением
игры. Это подтверждается следующим примером.
Пример 6.3. Дилемма заключенного. Конкурс на реализацию
проекта.
⎛ − 8 − 2⎞
⎛ − 8 − 10 ⎞
⎟⎟, B = ⎜⎜
⎟⎟.
A = ⎜⎜
⎝ − 10 − 4 ⎠
⎝− 2 − 4 ⎠
Интерпретируется этот пример так. "Игроками" являются двое
заключенных, обвиняемых в совершении тяжелого преступления, их
стратегиями - сознаваться или не сознаваться. Если оба сознаются (в матрице
это 1-я строка и 1-й столбец), то получат большой срок заключения, но не
максимальный. Если оба не сознаются (2-я строка и 2-й столбец), то их
осудят за менее тяжкие преступления, в которых они уже уличены. Наконец,
если сознается только один, то его срок заключения будет значительно
снижен, а другой получит максимальный срок. (Числа в матрицах - это сроки
заключения, взятые с противоположным знаком.) В этой игре (e1 , f1 ) единственная ситуация равновесия. Ситуация же ( e 2 , f 2 ) , более выгодная для
обоих игроков, равновесной не является, так как каждому игроку выгодно
односторонне отступить от стратегии, в нее входящей. Достаточно легко
найти экономический пример матрицы с подобной расстановкой
предпочтений (то есть с элементами матриц, находящимися в таком же
порядке по числовым значениям) – конкурс на реализацию проекта. Две
фирмы, борющиеся за заказ на определенную работу, могут выбрать два
варианта - подать развернутую программу(1-я стратегия) или простую
заявку(2-я стратегия). Согласно правилам при одинаковом выборе
конкурентов заказ и доход делятся пополам, а в другом случае предпочтение
отдается фирме, подавшей подробную заявку. На реализацию проекта
победителям (одному или двоим) выделяется 10 тысяч долларов.
Технические затраты на простую заявку - 1 тысяча долларов, на развернутую
программу - 3 тысячи долларов.
⎛ 2 7⎞
⎛ 2 − 1⎞
⎟⎟, B = ⎜⎜
⎟⎟ .
A = ⎜⎜
⎝ − 1 4⎠
⎝7 4 ⎠
Эти два примера (дилемма заключенного и борьба конкурсантов)
характеризуют важную особенность биматричных игр – возможность
наличия противоречия между выгодностью и устойчивостью. В обоих
случаях для обоих игроков выгодной является ситуация ( e 2 , f 2 ) , а
устойчивой - (e1 , f1 ) . Под неустойчивостью мы понимаем выгодность для
одного из игроков одностороннего отклонения от ситуации. Выход здесь – в
кооперации игроков.
Алгоритм поиска ситуации равновесия для биматричной игры
произвольной размерности достаточно сложен. Поэтому дадим описание
ситуаций равновесия только в биматричных играх размерности 2×2. Такая
игра задается парой матриц
a12 ⎞
b12 ⎞
⎛a
⎛b
⎟⎟, B = ⎜⎜ 11
⎟⎟.
A = ⎜⎜ 11
⎝ a 21 a 22 ⎠
⎝ b21 b22 ⎠
Примем без доказательства следующую
ТЕОРЕМУ 6.2. Если в биматричной игре Г элементы, стоящие в одном
столбце матрицы А, и элементы, стоящие в одной строке матрицы В, попарно
различны, то ситуации равновесия могут быть либо чистыми, либо вполне
смешанными (то есть такими, в которых обе чистые стратегии применяются
с положительными вероятностями). Вполне смешанная ситуация ( x, y ), где
x = ( x1 , x 2 ), y = ( y1 , y 2 )
будет ситуацией равновесия в игре Г при
выполнении следующих условий:
⎧b11 x1 + b21 x 2 = b12 x1 + b22 x 2 ;
⎪
(6.3)
⎨ x1 , x 2 > 0;
⎪ x + x = 1.
2
⎩ 1
⎧a11 y1 + a12 y 2 = a 21 y1 + a 22 y 2 ;
⎪
(6.4)
⎨ y1 , y 2 > 0;
⎪ y + y = 1.
2
⎩ 1
Введем следующие обозначения:
b22 − b21
;
(6.5)
β=
(b11 + b22 ) − (b12 + b21 )
a 22 − a12
.
(6.6)
α=
(a11 + a 22 ) − (a12 + a 21 )
Получаем, что система (6.3) имеет решение (единственное) тогда и
только тогда, когда 0 < β < 1 , причем в этом случае решение системы (6.3)
есть x1 = β , x 2 = 1 − β . Аналогичным образом получаем, что система (6.4)
имеет решение (единственное) тогда и только тогда, когда 0 < α < 1 , и в этом
случае решение системы (6.4) есть y1 = α , y 2 = 1 − α .
Итак, если 0 < α , β < 1 , то игра Г имеет вполне смешанную, причем
единственную,
ситуацию
равновесия
( x 0 , y 0 ),
где
x 0 = ( β , 1 − β ), y 0 = (α , 1 − α ).
Например, для игры «Семейный спор» смешанная ситуация равновесия
находится так:
0
1− 0 1
4 − 0 4 0 ⎛ 4 1⎞
⎛1 4⎞
α=
= , β=
= , x = ⎜ , ⎟, y = ⎜ , ⎟.
5−0 5
5−0 5
⎝ 5 5⎠
⎝5 5⎠
Выигрыш обоих игроков при использовании такой смешанной
4
стратегии составит .
5
Пример 6.4. Борьба за рынки сбыта.
Фирма а намерена сбыть партию товара на одном из двух рынков,
контролируемых более крупной фирмой b. С этой целью она проводит
подготовительную работу, связанную с определенными затратами. Если
фирма b разгадает - на каком из рынков фирма а будет продавать свой товар,
она примет контрмеры и воспрепятствует "захвату" рынка (этот вариант
означает поражение фирмы а); если нет, то фирма а одерживает победу.
Предположим, что для фирмы а проникновение на первый рынок более
выгодно, чем проникновение на второй, но и борьба на первом рынке требует
от нее больших средств. Например, победа фирмы а на первом рынке
приносит ей вдвое большую прибыль, чем победа на втором, но зато
поражение на первом рынке полностью ее разоряет. Составим
математическую модель этого конфликта, считая фирму а игроком 1 и фирму
b игроком 2. Стратегии игрока 1: первая - проникновение на рынок 1, вторая
- проникновение на рынок 2; стратегии игрока 2: первая - контрмеры на
рынке 1, вторая - контрмеры на рынке 2. Пусть для фирмы а ее победа на 1-м
рынке оценивается в 2 единицы, а победа на 2-м рынке - в 1 единицу;
поражение фирмы а на 1-м рынке оценивается в -10, а на 2-м в -1. Для фирмы
b ее победа составляет соответственно 5 и 1 единицу, а поражение -2 и -1.
Получаем в итоге биматричную игру Г с матрицами выигрышей
⎛ − 10 2 ⎞
⎛ 5 − 2⎞
⎟⎟, B = ⎜⎜
⎟⎟.
A = ⎜⎜
− 1⎠
⎝ 1
⎝−1 1 ⎠
По теореме 6.2 эта игра может иметь либо чистые, либо вполне
смешанные ситуации равновесия. Ситуаций равновесия в чистых стратегиях
здесь нет (содержательно этот факт можно объяснить следующим
рассуждением: если стратегия фирмы а была разгадана фирмой b, то в этой
ситуации отклонение выгодно для фирмы а; в противном случае отклонение
выгодно для фирмы b). Убедимся теперь, что данная игра имеет вполне
смешанную ситуацию равновесия. Действительно, из (6.6) и (6.5) находим
3
1+1 2
−1− 2
α=
= , β=
= .
6+3 9
− 11 − 3 14
Итак, рассматриваемая игра имеет единственную ситуацию равновесия
⎛2 7⎞
⎛ 3 11 ⎞
( x 0 , y 0 ), где x 0 = ⎜ , ⎟, y 0 = ⎜ , ⎟. Она может быть реализована при
⎝9 9⎠
⎝ 14 14 ⎠
многократном повторении игры (то есть при многократном воспроизведении
описанной ситуации) следующим образом: фирма а должна использовать
чистые стратегии 1 и 2 с частотами 2/9 и 7/9, а фирма b - чистые стратегии 1
и 2 с частотами 3/14 и 11/14. Любая из фирм, отклонившись от указанной
смешанной стратегии, уменьшает свой ожидаемый выигрыш (однако, это не
означает, как в случае антагонистических игр, что другая фирма увеличивает
при этом свой ожидаемый выигрыш).
Пример 6.5. Соперничество в области технологического лидерства.
Этот пример примитивен в вычислительном плане, но содержателен.
Предприятие 1 ранее обладало технологическим превосходством, но в
настоящее время располагает меньшими финансовыми ресурсами для
научных исследований и разработок (НИР), чем его конкурент. Оба
предприятия должны решить, стоит ли пытаться с помощью крупных
капиталовложений добиться доминирующего положения на мировом рынке в
соответствующей технологической области. Если оба конкурента вложат в
дело крупные средства, то перспективы на успех у предприятия 1 будут
лучше, хотя оно и понесет большие финансовые расходы (как и предприятие
2). Эта ситуация представлена платежами с отрицательными значениями.
Первая стратегия у предприятия 1 – низкие затраты на НИР, у предприятия
2 – неучастие в технологической конкуренции. Вторая стратегия у каждого
игрока – высокие затраты на НИР. Для предприятия 1 лучше всего было бы,
если бы предприятие 2 отказалось от конкуренции. Его выгода в таком
случае составила бы 3 (платежа). С большой вероятностью предприятие 2
выиграло бы соперничество, когда предприятие 1 приняло бы урезанную
программу инвестиций, а предприятие 2 – более широкую.
⎛3 1 ⎞
⎛0 3 ⎞
⎟⎟, B = ⎜⎜
⎟⎟.
A = ⎜⎜
⎝ 0 − 1⎠
⎝0 − 2⎠
Анализ матрицы показывает, что равновесие в чистых стратегиях
наступает при высоких затратах на НИР предприятия 2 и низких предприятия
1. При любом другом раскладе у одного из конкурентов появляется резон
отклониться от стратегической комбинации: так, для предприятия 1
предпочтителен сокращенный бюджет, если предприятие 2 откажется от
участия в соперничестве; в то же время предприятию 2 известно, что при
низких затратах конкурента ему выгодно инвестировать в НИР.
Предприятие, имеющее технологическое преимущество, может прибегнуть к
анализу ситуации на базе теории игр, чтобы, в конечном счете, добиться
оптимального для себя результата. С помощью определенного сигнала оно
должно показать, что готово осуществить крупные затраты на НИР. Если
такой сигнал не поступил, то для предприятия 2 ясно, что предприятие 1
выбирает вариант низких затрат. О достоверности сигнала должны
свидетельствовать обязательства предприятия, например, решение
предприятия 1 о закупке новых лабораторий или о найме на работу
дополнительного научно-исследовательского персонала.
Рассмотрим вкратце кооперативное поведение игроков в биматричных
играх. Безусловно, чем больше игроков, тем шире возможности для создания
коалиций, но и в биматричном случае противники могут в какой-то мере
успешно координировать свои действия.
Можно показать, что даже если ситуация равновесия Паретооптимальна, то и тогда возможны случаи, когда одна ситуация равновесия
выгодна одному игроку, а другая – другому. Разрешим игрокам совершать
совместные действия и, расширив, таким образом, множество стратегий,
будем искать оптимальные решения на этом множестве.
Вернемся
к
игре
«Семейный
спор».
Множество
точек,
соответствующих всем выигрышам в смешанных стратегиях, заштриховано
на рис. 6.1. Есть две чистых ситуации
G
равновесия и одна вполне смешанная с
⎛4 4⎞
(1,4)
вектором
выигрышей
⎜ , ⎟ . Как
4
⎝5 5⎠
видно из рисунка, чистые ситуации
(5/2,5/2)
равновесия Парето-оптимальны. Если
3
игра повторяется многократно, то
игрокам имеет смысл с вероятностью
2
0.5 выбирать каждую из двух чистых
(4,1)
(4/5,4/5)
равновесных стратегий. Тогда средний
1
выигрыш каждого составит 2.5
единицы.
Но
соответствующая
0
1
2
3
4
ситуации точка не лежит во множестве
Рис. 6.1
точек, определяемом правилами бескоалиционной биматричной игры, т.е. не
может быть реализована, если игроки выбирают свои стратегии независимо
друг от друга.
Совместной смешанной стратегией называют смешанную стратегию,
на которую согласны оба игрока (Это вероятностное распределение на
множестве всевозможных пар (i,j), не обязательно порожденное независимым
случайным выбором чистых стратегий игроками 1 и 2). Предполагается, что
такие стратегии могут быть реализованы посредником в переговорах до
начала игры. Обозначим буквой M совместную смешанную стратегию в игре
Г. Тогда ожидаемые выигрыши F (M ) и G( M ) игроков 1 и 2 соответственно
определяются как математические ожидания выигрышей
на чистых
стратегиях:
n
m
n
m
F (M ) = ∑ ∑ a ij μ ij ;G (M ) = ∑ ∑ bij μ ij .
i =1 j =1
i =1 j =1
В биматричной игре размерности n×m любая совместная смешанная
стратегия задается матрицей n×m, элементы матрицы неотрицательны, их
сумма равна 1. Элемент μ ij − вероятность того, что 1-й игрок выберет i-ю
стратегию, а 2-й игрок – j-ю стратегию.
Геометрическое
G
изображение множества точек,
соответствующего
множеству
(1,4)
векторов
выигрышей
в 4
совместных
смешанных
стратегиях для игры «Семейный
(5/2,5/2)
спор» приведено на рис. 6.2. Это 3
выпуклая оболочка множества
точек возможных выигрышей в 2
(4,1)
(4/5,4/5)
чистых стратегиях. Совместной
*
смешанной
стратегии
M= 1
⎛1
⎞
⎜ 2 0 ⎟
1
2
3
4
F
соответствует 0
⎜ 0 1 ⎟
Рис. 6.2
⎝
2⎠
оптимальный по Парето вектор
выигрышей (5/2,5/2). Таким образом, M* может быть рекомендована в
качестве решения игры «Семейный спор».
Для игры в совместных смешанных стратегиях также вводится
понятие ситуации равновесия. В биматричной игре Г размерности n×m
обозначим через M= μ ij совместное вероятностное распределение на парах
каждого
i(или
j)
введем
(i, j ), i = 1,...., n j = 1,...., m. Для
μ i ( j ) (или ν j (i ) соответственно) - условную вероятность реализации j(или i
соответственно). По определению эти вероятности таковы:
{ }
m
⎧ μ ij
,
если
μ ik ≠ 0
∑
m
⎪
k
=
1
⎪⎪
∑ μ ik
.
μi ( j) = ⎨
k =1
⎪
m
⎪0, если ∑ μ ik = 0
⎪⎩
k =1
n
⎧ μ ij
,
если
∑ μ kj ≠ 0
n
⎪
k =1
⎪⎪
∑ μ kj
ν j (i ) = ⎨
.
k =1
⎪
n
⎪0, если ∑ μ kj = 0
⎪⎩
k =1
Определение. Будем говорить, что M*= μ ij* - ситуация равновесия в
совместных смешанных стратегиях в игре Г, если выполнены неравенства
{ }
m
∑
j =1
a ij μ i*
m
( j ) ≥ ∑ a kj μ k* ( j )
j =1
n
n
i =1
i =1
(6.7)
∑ bijν *j (i ) ≥ ∑ bilν l* (i )
∀i, k ∈ {1,...., n}, j , l ∈ {1,...., m}.
Игру Г в совместных смешанных стратегиях можно интерпретировать
так. Пусть игроки договорились об использовании стратегии M * , и после
реализации случайного механизма 1-й игрок получил стратегию i , а 2-й –
стратегию j . Каждый игрок знает только свою реализацию. Каждый может
не согласиться с реализацией, отведенной ему, и выбрать соответственно
стратегию k или l . Тогда любому из игроков невыгодно односторонне
отклониться от предложенной реализации, если M * - равновесна (это
следует из (6.7), где слева в неравенствах стоят выигрыши игроков в случае
согласия с реализацией i(j) ).
Примем без доказательства следующую
ТЕОРЕМУ 6.3.
Множество ситуаций равновесия в совместных смешанных стратегиях
биматричной игры размерности n×m является непустым выпуклым
компактом в пространстве R n + m .
Если x, y - пара смешанных стратегий игроков 1 и 2, то определяемая
по ним ситуация M= μ ij в совместных смешанных стратегиях будет
( )
{ }
( )
равновесной тогда и только тогда, когда x, y - ситуация равновесия в игре
Г.
С помощью этой теоремы можно проверить, что, например, в игре
⎛1
0 ⎞⎟
* ⎜ 2
«Семейный спор» стратегия M =
- равновесна.
⎜ 0 1 ⎟
⎝
2⎠
Итак, очевидно, что координация действий приносит ощутимые
выгоды обоим игрокам. При определенных условиях часть выигрыша по
договоренности может также передаваться от одного игрока к другому.
Возникает естественный вопрос о том, как разумным игрокам прийти к
соглашению при совместном выборе решения в ходе переговоров. Но ответ
на этот вопрос выходит за рамки пособия.
Вопросы для самоконтроля по курсу "Теория игр"
1.
ПРИНЯТИЕ
НЕОПРЕДЕЛЕННОСТИ
РЕШЕНИЯ
В
УСЛОВИЯХ
1. Как системно описывается задача принятия решения в условиях
неопределенности?
2. Что такое управляющая подсистема, что такое среда?
3. Какими факторами определяется состояние системы?
4. Сформулируйте математическую модель задачи принятия решения в
условиях неопределенности. Что такое функция полезности (выигрыша)?
Что такое условие неопределенности?
5.Как задают функцию выигрыша при условии конечности множеств
стратегий и состояний?
6.Какова основная цель задачи принятия решения?
7.Как в теории игр называют задачу принятия решения в условиях
неопределенности?
8.Что понимают под оптимальной стратегией игрока?
9.Как задают игру в случае, если множества X и Y конечны?
10.Какие имеются способы сравнения двух стратегий?
11.Что такое принцип доминирования?
12.Каков основной метод, позволяющий найти оптимальную стратегию
в ЗПР в условиях неопределенности? Какая стратегия считается
оптимальной?
13.Что такое критерий для сравнения стратегий?
14.Каковы важнейшие критерии, используемые для задач принятия
решений в условиях неопределенности? На каких гипотезах они основаны?
2. ПРИНЯТИЕ РЕШЕНИЯ В УСЛОВИЯХ РИСКА
1.Как задается вероятностная мера на множестве состояний природы,
если множество конечно?
2.Что такое априорное распределение вероятностей на множестве
состояний природы.
3.В каких случаях говорят, что принятие решения происходит в
условиях риска?
4.Как определяется критерий математического ожидания?
5.Что такое байесовская стратегия, байесовский подход?
3. АНТАГОНИСТИЧЕСКИЕ ИГРЫ
1. Как называется задача принятия решения, в которых на систему
воздействует не одна, а несколько управляющих подсистем, каждая из
которых имеет свои цели и возможности действий?
2.
Математическая
модель
какого
конфликта
называется
антагонистической игрой?
3. Чем определяется состояние такой системы? Антагонистическую
игру естественно задать системой Г=(Х, Y, F).
4. Какая игра называется антагонистической и какими объектами ее
задают?
5. В чем содержательное различие между управляющей подсистемой и
средой ?
6. Как называется антагонистическая игра, если Х и Y конечны?
7. Как определяются нижняя цена игры и верхняя цена игры? Как
определяется цена игры?
8. Каково соотношение между максимином и минимаксом?
9. Что такое седловая точка? К чему приводит одностороннее
отступление игрока от седловой точки?
10. Чему равно значение функции выигрыша в седловой точке?
11.Сформулируйте теорему о взаимозаменяемости и эквивалентности
cедловых точек.
12. Сформируйте достаточное условие существования седловой точки.
13. При каких условиях в выпуклой игре у игрока есть единственная
оптимальная стратегия?
4. ТЕОРИЯ МАТРИЧНЫХ ИГР
1. По какому алгоритму происходит поиск седловой точки в матричной
игре?
2. Всегда ли в матричной игре есть седловые точки?
3. Каким образом можно выбирать свои стратегии случайно?
4. Что такое чистая стратегия игрока?
5. Что такое смешанная стратегия игрока в в матричной игре и как она
задается?
6. Что собой представляют содержательно компоненты смешанной
стратегии?
7. Как определяется функция выигрыша игрока на смешанных
стратегиях?
8. Как задается матричная игра со смешанными стратегиями? Какими
свойствами обладают стратегии?
9. Сформулируйте основную теорему теории матричных игр.
10. Приведите критерии оптимальности стратегий игроков.
11. Какова структура множества оптимальных стратегий каждого
игрока?
12. Сформулируйте теорему о достижимости
максимумов и
минимумов функций выигрыша на чистых стратегиях.
13. Какие чистые стратегии входят в качестве компонент седловой
точки с положительной вероятностью?
14. Что такое выпуклая комбинация векторов?
15. В каком случае говорят, что один вектор доминирует(строго
доминирует) другой?
16. Сформулируйте теорему о доминировании.
5. МЕТОДЫ РЕШЕНИЯ МАТРИЧНЫХ ИГР
1.Как находят смешанные оптимальные стратегии для игры 2*2? Как
находят для такой игры цену игры?
2. Как находят графическим методом оптимальные стратегии игроков в
игре 2*m? На какой теореме основана эта методика?
3.Как можно использовать графический метод для игр m*2?
4.Опишите графический метод для игр 3*3?
5.Опишите метод Брауна-Робинсон.
6.Является ли метод Брауна-Робинсон аналитическим, или же
итеративным?
7.На что опирается игрок при выборе своей стратегии на каждом шаге
по методу Брауна-Робинсон?
8.Имеются ли при использовании метода Брауна-Робинсон
ограничения по размерности матриц?
9.Что делает игрок, если стратегий, удовлетворяющих условию
выбора, несколько?
10.Как игроками выбираются начальные стратегии?
11. К чему, согласно методу Брауна-Робинсон, стремятся
воображаемые платежи υ1 ( k ) и υ 2 (k ) ?
6. БИМАТРИЧНЫЕ ИГРЫ
1. В каком случае возникает биматричная игра, чем она задается?
2. Как можно задать функции выигрыша игроков?
3. Как определяются смешанные стратегии игроков и функции
выигрыша игроков?
4. Как определяется ситуация равновесия в биматричной игре?
5. В чем содержательный смысл ситуации равновесия ?
6. В каком смысле седловая точка является частным случаем ситуации
равновесия?
7. Какая пара стратегий игроков называется оптимальной по Парето?
8. Что означает содержательно оптимальность по Парето?
9. В чем формальное различие между ситуацией равновесия и
ситуацией, оптимальной по Парето?
10.Как связаны ситуация равновесия и Парето-оптимальная стратегия в
матричных играх?
11. Всегда ли в биматричной игре есть ситуация равновесия?
12.Сформулируйте теорему Брауэра.
13.Всегда ли в биматричной игре есть чистая ситуация равновесия?
14.Являются ли разными ситуации равновесия эквивалентными по
значениям функций выигрыша.
15.Что понимается под возможной в игре неустойчивостью ситуации
равновесия?
16. Опишите алгоритм поиска ситуации равновесия в биматричных
играх размерности 2×2. Что такое вполне смешанные стратегии?
17.Что такое совместная смешанная стратегия? Как могут быть
реализованы на практике такие стратегии?
18.Как определяются выигрыши игроков при совместной смешанной
стратегии?
19. Как задается в биматричной игре совместная смешанная стратегия?
20. Как определяется в биматричной игре ситуация равновесия в
совместных смешанных стратегиях?
21. Какова структура множества ситуаций равновесия в совместных
смешанных стратегиях биматричной игры размерности n×m?
22. Какова связь между ситуациями равновесия в смешанных и в
совместных смешанных стратегиях?
Задачи для самостоятельного решения
1. Дана задача принятия решения. В таблице - прибыль города при
различных вариантах проведения праздника (тыс. руб.).
Погода
Солнечно (60 %)
Дождь (40 %)
Праздник на открытом воздухе
1000
200
Праздник в театре
750
500
Установить, где следует проводить праздник по критериям Лапласа,
Вальда и математического ожидания? Каким будет α в критерии Гурвица,
если предпочтение отдано театру?
5
Ответ: в театре, в театре, на открытом воздухе, α > .
11
2. Найти в антагонистической игре седловую точку, если она есть.
⎡ π⎤
⎡ π⎤
X = ⎢0; ⎥;Y = ⎢0; ⎥; F ( x , y ) = sin( x + y ) .
⎣ 2⎦
⎣ 2⎦
Ответ: седловой точки нет.
π
Ответ: (0,1).
X = [0;1];Y = [0;1]; F ( x, y ) = sin( xy ).
2
⎛ x 2 3⎞
⎜
⎟
3. Матрица А в матричной игре имеет вид ⎜ y 5 4 ⎟ .
⎜ 6 7 8⎟
⎝
⎠
Установить, при каких x и y в матрице есть седловые точки.
Ответ: при x ≤ 6, y ≤ 6.
⎛ x 1 2⎞
⎜
⎟
4. Матрица А в матричной игре имеет вид ⎜ 5 2 0 ⎟ .
⎜ 3 3 0⎟
⎝
⎠
Установить, при каких x в матрице есть седловые точки.
Ответ: при любых значениях х седловых точек нет.
5. Задача о зимней эксплуатация лесовозной дороги.
Предположим, что при заготовке леса зимой есть выбор - делать или не
делать предварительную расчистку дороги. При этом известны
предполагаемые высоты снежного покрова и матрица доходов при
применении той или иной стратегии. Заготовитель – игрок 1, природа – игрок
2.
1\2
Не делать
Делать
20 мм
2
4
40 мм
2
3
60 мм
3
2
100 мм
-1
6
Найти цену игры.
Ответ: v=2.5.
6. Найти с помощью
доминируемый столбец
⎛ 7 9 10 8
⎜
матрицей A= ⎜ 8 3 2 4
⎜6 2 1 3
⎝
графического метода, предварительно вычеркнув
или строку, решение матричной игры с
11⎞
⎟
1 ⎟.
0 ⎟⎠
Ответ: x = (0.8,0.2,0); y = (0.8,0,0,0.2,0), v = 7.2
7. Найти
оптимальные
стратегии
игроков в
⎛ − 1 3 − 3⎞
⎜
⎟
матрицей A = ⎜ 2 0 − 3 ⎟ .
⎜ 2 1 0 ⎟
⎝
⎠
игре
с
Ответ: x = (1/3,2/3,0); y = (1/5,3/5,1/5).
⎛ 1 2 3⎞
⎜
⎟
8. Матрица А в биматричной игре имеет вид ⎜ 2 1 3 ⎟ .
⎜ 2 3 1⎟
⎝
⎠
Установить, какой должна быть матрица B, чтобы игра имела чистые
ситуации равновесия.
Ответ: должно выполняться хотя бы одно из трех условий:
a) b13 − максимум в первой строке; б) во второй строке есть элементы,
не меньшие, чем b22 ; в) в третьей строке есть элементы, не меньшие, чем b33 .
9. Найти смешанные ситуации равновесия в игре с матрицами
⎛3 2⎞
⎛ 2 4⎞
⎟⎟ , B= ⎜⎜
⎟⎟ .
A= ⎜⎜
1
6
1
0
⎠
⎝
⎠
⎝
Ответ: x = (2/5,3/5); y = (2/3,1/3).
Тесты по курсу "Теория игр"
1.При каких значениях α критерий Гурвица обращается в критерий Вальда?
а)>0.
б)=1.
в)<0.
2.В чем отличие критерия Сэвиджа от остальных изученных критериев
принятия решения:
а) Он минимизируется.
б) Он максимизируется.
в) Он не всегда дает однозначный ответ.
3.Антагонистическая игра может быть задана:
а) множеством стратегий обоих игроков и седловой точкой.
б) множеством стратегий обоих игроков и функцией выигрыша первого
игрока.
4.Матричная игра – это частный случай антагонистической игры, при
котором обязательно выполняется одно из требований:
а) один из игроков имеет бесконечное число стратегий.
б) оба игрока имеют бесконечно много стратегий.
в) оба игрока имеют одно и то же число стратегий.
г) оба игрока имеют конечное число стратегий.
5.Пусть матричная игра задана матрицей, в которой все элементы
положительны. Цена игры положительна:
а) да.
б) нет.
в) нет однозначного ответа.
6.Цена игры всегда меньше верхней цены игры, если обе цены существуют:
а) да.
б) нет.
в) вопрос некорректен.
7.Оптимальная смешанная стратегия для матричной игры меньше любой
другой стратегии.
а) да.
б) нет.
в) вопрос некорректен.
г) нет однозначного ответа.
8.Цена игры существует для матричных игр в смешанных стратегиях всегда.
а) да.
б) нет.
9.Каких стратегий в матричной игре размерности, отличной от 1*,
больше:
а) чистых.
б) смешанных.
в) поровну и тех, и тех.
10.Если в матрице все столбцы одинаковы и имеют вид ( 4 5 0 1), то какая
стратегия оптимальна для 2-го игрока?
а) первая.
б)вторая.
в)любая из четырех.
11.Какое максимальное число седловых точек может быть в игре
размерности 2*3 (матрица может содержать любые числа)
а) 2.
б)3.
в)6.
12. Максимум по x минимума по y и минимум по y максимума по x функции
выигрыша первого игрока:
а) всегда разные числа, первое больше второго.
б) не всегда разные числа; первое не больше второго.
в) связаны каким-то иным образом.
13. Могут ли в какой-то антагонистической игре значения функции
выигрыша обоих игроков для некоторых значений переменных быть равны
одному числу?
а)да, при нескольких значениях этого числа.
б) нет.
в) да, всего при одном значении этого числа.
14.Пусть в антагонистической игре X=(1;2)- множество стратегий 1-го
игрока, Y=(5;8)- множество стратегий 2-го игрока. Является ли пара (1;5)
седловой точкой в этой игре:
а) всегда.
б) иногда.
в) никогда.
15.В матричной игре размерности 2*2 есть 4 седловых точки?
а) Всегда.
б) иногда.
в) никогда.
16.Пусть в матричной игре одна из смешанных стратегий 1-го игрока имеет
вид (0.3, 0.7), а одна из смешанных стратегий 2-го игрока имеет вид ( 0.4, 0,
0.6). Какова размерность этой матрицы?
а) 2*3.
б) 3*2.
в) другая размерность.
17.Если известно, что функция выигрыша 1-го игрока равна числу 1 в
седловой точке, то значения этой функции могут принимать значения:
а) любые.
б) только положительные.
в) только не более числа 1.
18. Принцип доминирования позволяет удалять из матрицы за один шаг:
а) целиком строки.
б) отдельные числа.
в) подматрицы меньших размеров.
19.В графическом методе решения игр 2*m непосредственно из графика
находят:
а) оптимальные стратегии обоих игроков.
б) цену игры и оптимальную стратегию 2-го игрока.
в) цену игры и оптимальную стратегию 1-го игрока.
20.График нижней огибающей для графического метода решения игр 2*m
представляет собой в общем случае:
а) ломаную.
б) прямую.
в) параболу.
21. Если в антагонистической игре на отрезке [0;1]*[0;1] функция выигрыша
1-го игрока F(x,y) равна C(x-y)^2, то в зависимости от C:
а) седловых точек нет никогда.
б) седловые точки есть всегда.
в) третий вариант.
22.Чем можно задать матричную игру:
а) одной матрицей.
б) двумя матрицами.
в) ценой игры.
23. В матричной игре произвольной размерности смешанная стратегия
любого игрока – это:
а) число.
б) множество.
в) вектор, или упорядоченное множество.
г) функция.
24. В матричной игре 2*2 две компоненты смешанной стратегии игрока:
а) определяют значения друг друга.
б) независимы.
25. Биматричная игра может быть определена:
а) двумя матрицами только с положительными элементами.
б) двумя произвольными матрицами.
в) одной матрицей.
26. В матричной игре элемент aij представляет собой:
а) выигрыш 1-го игрока при использовании им i-й стратегии, а 2-м – j-й
стратегии.
б) оптимальную стратегию 1-го игрока при использовании противником i-й
или j-й стратегии.
в) проигрыш 1-го игрока при использовании им j-й стратегии, а 2-м – i-й
стратегии.
27.Элемент матрицы aij соответствует седловой точке. Возможны следующие
ситуации:
а) этот элемент строго меньше всех в строке.
б) этот элемент второй по порядку в строке.
в) в строке есть элементы и больше, и меньше, чем этот элемент.
28. В биматричной игре размерности 3*3 ситуаций равновесия бывает:
а) не более 3.
б) не менее 6.
в) не более 9.
29. В методе Брауна-Робинсон каждый игрок при выборе стратегии на
следующем шаге руководствуется:
а) стратегиями противника на предыдущих шагах.
б) своими стратегиями на предыдущих шагах.
в) чем-то еще.
30. По критерию математического ожидания каждый игрок исходит из того,
что:
а) случится наихудшая для него ситуация.
б) все ситуации равновозможны.
в) все или некоторые ситуации возможны с некоторыми заданными
вероятностями.
31. Антагонистическая игра может быть задана:
а) множеством стратегий игроков и ценой игры.
б) множеством стратегий обоих игроков и функцией выигрыша второго
игрока.
в) чем-то еще.
32. Матричная игра – это частный случай антагонистической игры, при
котором обязательно выполняется одно из требований:
а) один из игроков выигрывает.
б) игроки имеют разное число стратегий.
в) можно перечислить стратегии каждого игрока.
33. Пусть матричная игра задана матрицей, в которой все элементы
отрицательны. Цена игры положительна:
а) да.
б) нет.
в) нет однозначного ответа.
34. Цена игры меньше верхней цены игры, если оба показателя существуют.
а) да.
б) не всегда.
в) никогда.
35. Оптимальная смешанная стратегия для матричной игры не содержит
нулей:
а) да.
б) нет.
в) вопрос некорректен.
г) не всегда.
36. Цена игры - это:
а) число.
б) вектор.
в) матрица.
37. Каких стратегий в матричной игре больше:
а) оптимальных.
б) не являющихся оптимальными.
в) нет однозначного ответа.
38.Если в матрице все столбцы одинаковы и имеют вид ( 4 5 0 1), то какая
стратегия оптимальна для 1-го игрока:
а) первая чистая.
б) вторая чистая.
в) какая-либо смешанная.
39.Какое максимальное число седловых точек может быть в игре
размерности 5*5 ( матрица может содержать любые числа) :
а) 5.
б)10.
в)25.
40.Пусть в антагонистической игре X=(1;2)- множество стратегий 1-го
игрока, Y=(2;8)- множество стратегий 2-го игрока. Является ли пара (2;2)
седловой точкой в этой игре :
а) всегда.
б) иногда.
в) никогда.
41.Бывает ли в биматричной игре (размерности 3*3) 4 ситуации равновесия?
а) Всегда.
б) иногда.
в) никогда.
42. Пусть в матричной игре размерности 2*3 одна из смешанных стратегий
1-го игрока имеет вид (0.3, 0.7), а одна из смешанных стратегий 2-го игрока
имеет вид ( 0.3, x, 0.5). Чему равно число x?
а)0.4.
б)0.2.
в) другому числу.
43.Матричная игра – это частный случай биматричной, при котором: а)
матрицы А и В совпадают.
б) из матрицы A можно получить матрицу В путем транспонирования.
в) выполняется что-то третье.
44. В биматричной игре элемент bij представляет собой:
а) выигрыш 1-го игрока при использовании им i-й стратегии, а 2-м – j-й
стратегии.
б) оптимальную стратегию 1-го игрока при использовании противником i-й
или j-й стратегии.
в) выигрыш 2-го игрока при использовании им j-й стратегии, а 1-м – i-й
стратегии.
45. В биматричной игре элемент aij соответствует ситуации равновесия.
Возможны следующие ситуации:
а) этот элемент строго меньше всех в столбце.
б) этот элемент больше всех в строке.
в) в столбце есть элементы и больше, и меньше, чем этот элемент.
46. В матричной игре, зная стратегии каждого игрока, можно найти цену
игры:
а) да.
б) нет.
в) вопрос некорректен.
47. Для какой размерности игровой матрицы критерий Вальда обращается в
критерий Лапласа?
а)1*5
б)5*1
в)только в других случаях.
48. В чем отличие критерия Вальда от остальных изученных критериев
принятия решения:
а) Он минимизируется
б) Он максимизируется
в) При расчете не используются арифметические операции сложения и
вычитания.
49.Антагонистическая игра может быть задана:
а) седловыми точками.
б) множеством стратегий обоих игроков и функцией выигрыша второго
игрока.
в)седловой точкой и ценой игры.
50.Матричная игра – это частный случай антагонистической игры, при
котором обязательно выполняется одно из требований:
а) один из игроков выигрывает.
б) функция выигрыша игрока может быть задана матрицей.
в) стратегии игроков задаются матрицей.
51.Пусть матричная игра задана матрицей, в которой все элементы
неотрицательны. Цена игры положительна:
а) да,
б) нет.
в) нет однозначного ответа.
52. Верхняя цена игры всегда меньше нижней цены игры.
а) да.
б) нет.
б) вопрос некорректен.
53. Оптимальная стратегия для матричной игры не единственна:
а) да.
б) нет.
в) вопрос некорректен.
г) нет однозначного ответа.
54. Цена игры существует для матричных игр в чистых стратегиях всегда.
А) да.
б) нет.
в) вопрос некорректен.
55. Какие стратегии бывают в матричной игре:
а) чистые.
б) смешанные.
в) и те, и те.
56. Если в игровой матрице все строки одинаковы и имеют вид ( 4 5 0 1), то
какая стратегия оптимальна для 1-го игрока?
а) первая чистая.
б) вторая чистая.
в)любая.
57. Какое максимальное число седловых точек может быть в игре
размерности 5*6 ( матрица может содержать любые числа) :
а) 5.
б)11.
в)30.
58. Максимум по x минимума по y и минимум по y максимума по x функции
выигрыша первого игрока:
а) всегда одинаковые числа.
б) всегда разные числа.
в) ни то, ни другое.
59. Могут ли в какой-то антагонистической игре значения функции
выигрыша обоих игроков для некоторых значений переменных равняться 1?
а) всегда.
б) иногда.
в) никогда.
60. Пусть в антагонистической игре X=(1,2)- множество стратегий 1-го
игрока, Y=(5,8)- множество стратегий 2-го игрока( по две стратегии у
каждого). Является ли пара ( 1;2) седловой точкой в этой игре :
а) всегда.
б) иногда.
в) никогда.
61.Бывает ли в матричной игре размерности 2*2 1 седловая точка?
а) Всегда.
б) иногда.
в) никогда.
62.Пусть в матричной игре одна из смешанных стратегий 1-го игрока имеет
вид (0.3, 0.7), а одна из смешанных стратегий 2-го игрока имеет вид ( 0.4,
0.1,0.1,0.4). Какова размерность этой матрицы?
а)2*4.
б)6*1.
в) иная размерность.
63. Если известно, что функция выигрыша 1-го игрока равна числу 2 в
седловой точке, то значения этой функции могут принимать значения:
а) любые.
б) только положительные.
в) только не более числа 2.
64. Принцип доминирования позволяет удалять из матрицы за один шаг:
а) целиком столбцы,
б) отдельные числа.
в) подматрицы меньших размеров.
65. В графическом методе решения игр 3*3 для нахождения оптимальных
стратегий игроков:
а) строится два треугольника.
б) строится один треугольник.
в) треугольники не строятся вовсе.
66. График нижней огибающей для графического метода решения игр 2*m
представляет в общем случае функцию:
а) монотонно убывающую.
б) монотонно возрастающую.
в) немотонную.
67. Если в антагонистической игре на отрезке [0;1] функция выигрыша 1-го
игрока F(x,y) равна 2*x+C, то в зависимости от C:
а) седловых точек нет никогда.
б) седловые точки есть всегда.
в) иной вариант
68.Чем можно задать задачу принятия решения в условиях неопределенности
на конечных множествах:
а) двумя матрицами.
б) выигрышами.
в) чем-то еще.
69. В антагонистической игре произвольной размерности выигрыш первого
игрока – это:
а) число.
б) множество.
в) вектор, или упорядоченное множество.
г) функция.
70. В матричной игре 3*3 две компоненты смешанной стратегии игрока:
а) определяют третью.
б) не определяют.
71. Биматричная игра может быть определена:
а) двумя матрицами одинаковой размерности с произвольными элементами,
б) двумя матрицами не обязательно одинаковой размерности,
в) одной матрицей.
72. В матричной игре элемент aij представляет собой:
а) проигрыш 2-го игрока при использовании им j-й стратегии, а 2-м – i-й
стратегии.
б) оптимальную стратегию 2-го игрока при использовании противником i-й
или j-й стратегии,
в) выигрыш 1-го игрока при использовании им j-й стратегии, а 2-м – i-й
стратегии,
73. Элемент матрицы aij соответствует седловой точке. Возможны
следующие ситуации:
а) этот элемент строго больше всех в столбце.
б) этот элемент строго больше всех по порядку в строке.
в) в строке есть элементы и больше, и меньше, чем этот элемент.
74.В биматричной игре размерности 4*4 может быть ситуаций равновесия:
а) не более 4.
б) не более 8.
в) не более 16.
75.В методе Брауна-Робинсон каждый игрок при выборе стратегии на
следующем шаге руководствуется:
а) стратегиями противника на предыдущих шагах.
б) стратегиями противника в будущем.
в) своими стратегиями.
76. По критерию Вальда каждый игрок исходит из того, что:
а)случится наиболее плохая для него ситуация.
б) все ситуации равновозможны.
в) все ситуации возможны с некоторыми заданными вероятностями.
77. Антагонистическая игра может быть задана:
а) множеством стратегий игроков и ценой игры.
б) множеством стратегий первого игрока и функцией выигрыша второго
игрока.
в) чем-то еще.
78. Матричная игра – это частный случай антагонистической игры, при
котором иногда выполняется только одно из требований:
а) выигрыш первого игрока не равен проигрышу второго.
б) игроки имеют равное число стратегий.
в) множество стратегий каждого - более чем счетное множество.
79. Пусть матричная игра задана матрицей, в которой все элементы
отрицательны. Цена игры может быть равной нулю:
а) да.
б) нет.
в) нет однозначного ответа.
80. Нижняя цена меньше верхней цены игры:
а) да.
б) не всегда.
б) никогда.
81. Сумма компонент смешанной стратегия для матричной игры всегда:
а) равна 1.
б) неотрицательна.
в) положительна.
г) не всегда.
82. Смешанная стратегия - это:
а) число.
б) вектор.
в) матрица.
83. Каких стратегий в матричной игре больше:
а) оптимальных.
б) чистых.
в) нет однозначного ответа.
84. Если в матрице все столбцы одинаковы и имеют вид ( 4 3 0 2), то какая
стратегия оптимальна для 2-го игрока?
a)первая.
б)третья.
в)любая.
85. Какое максимальное число седловых точек может быть в игре
размерности 3*3 ( матрица может содержать любые числа):
а) 3.
б)9.
в)27.
86.Пусть в антагонистической игре X=(1;5)- множество стратегий 1-го
игрока, Y=(2;8)- множество стратегий 2-го игрока. Является ли пара (1,2)
быть седловой точкой в этой игре :
а) всегда.
б) иногда.
в) никогда.
87. Бывает ли в биматричной игре размерности 3*3 ровно 2 ситуации
равновесия?
а) Всегда.
б) иногда.
в) никогда.
88. Пусть в матричной игре размерности 2*3 одна из смешанных стратегий
1-го игрока имеет вид (0.3, 0.7), а одна из смешанных стратегий 2-го игрока
имеет вид ( 0.3, x, x). Чему равно число x?
а)0.7
б)0.4
в)чему-то еще.
89. Матричная игра – это частный случай биматричной, при котором всегда
справедливо:
а) матрица А равна матрице В, взятой с обратным знаком.
б) матрица A равна матрице В.
в) Произведение матриц А и В -единичная матрица..
90. В биматричной игре элемент bij представляет собой:
а) выигрыш 2-го игрока при использовании им i-й стратегии, а 1-м – j-й
стратегии,
б) оптимальную стратегию 2-го игрока при использовании противником i-й
или j-й стратегии/
в) что-то иное.
91.В биматричной игре элемент aij соответствует ситуации равновесия.
Возможны следующие ситуации:
а) в столбце есть элементы, равные этому элементу.
б) этот элемент меньше некоторых в столбце.
в) этот элемент меньше всех в столбце.
92. В матричной игре, зная стратегии каждого игрока и функцию выигрыша,
цену игры в чистых стратегиях, можно найти:
а) всегда.
б) иногда.
в) вопрос некорректен.
СПИСОК РЕКОМЕНДУЕМОЙ ЛИТЕРАТУРЫ
Основная
1. Розен В.В. Теория игр и экономическое моделирование. Саратов, 1996.
2. Шолпо И.А. Исследование операций. Теория игр. Саратов: Изд-во Сарат. унта, 1983.
3. Кузнецова И.А. Сборник задач по исследованию операций с методическими
указаниями. Саратов: Изд-во Сарат. ун-та, 1989.
Дополнительная
4. Гермейер Ю.Б. Игры с непротивоположными интересами. М.: Наука, 1976.
5. Кукушкин Н.С., Морозов В.В. Теория неантагонистических игр. М.: Изд-во
Моск. ун-та, 1984.
6. Воробьев Н.Н. Теория игр для экономистов-кибернетиков. М.: Наука, 1985.
7. Мулен Э. Теория игр с примерами из математической экономики. М.: Мир, 1985.
8. Зенкевич Н.А., Ширяев В.Д. Игры со многими участниками. Саранск: Изд-во
Мордовского ун-та, 1989.
9. Зенкевич Н.А., Еськова В.А. Конечные антагонистические игры. Кемерово:
Изд-во Кемеровского ун-та, 1989.
10. Харшаньи Дж., Зельтен Р. Общая теория выбора равновесия в играх. СПб.:
Экономическая школа, 2001.