Метод деления отрезка пополам Пусть дано уравнение 0 ) ( = x f

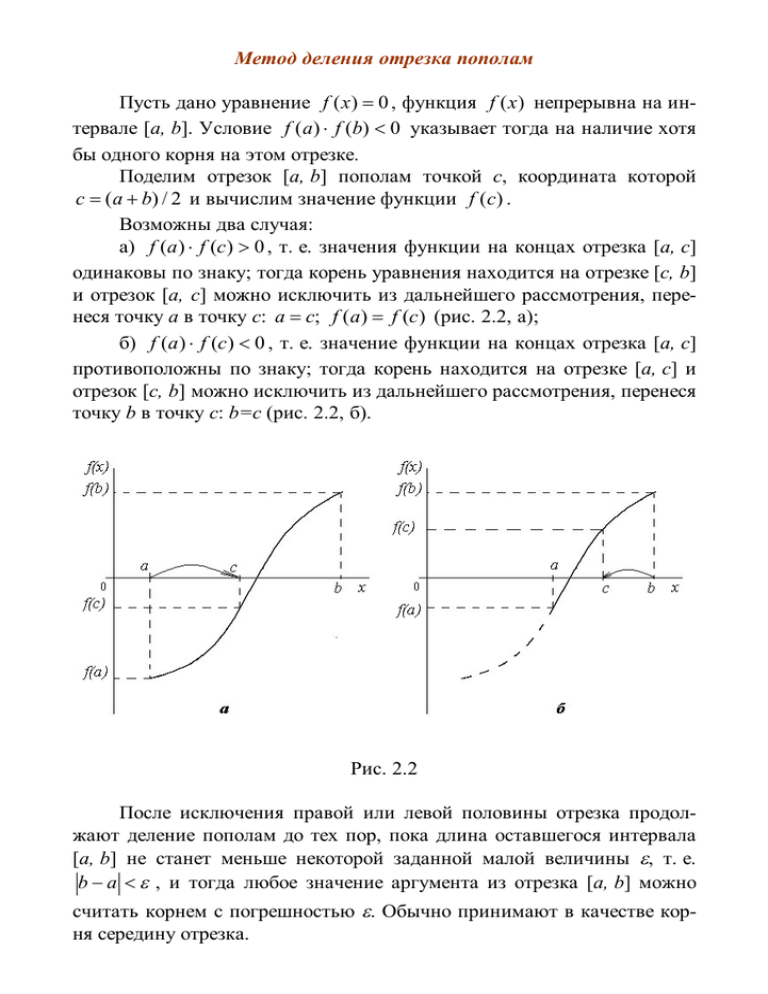
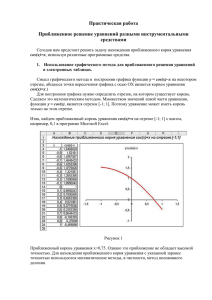
Метод деления отрезка пополам
Пусть дано уравнение f ( x )  0 , функция f (x ) непрерывна на интервале [a, b]. Условие f ( a)  f (b)  0 указывает тогда на наличие хотя
бы одного корня на этом отрезке.
Поделим отрезок [a, b] пополам точкой c, координата которой
c  ( a  b) / 2 и вычислим значение функции f (c) .
Возможны два случая:
а) f (a )  f (c )  0 , т. е. значения функции на концах отрезка [a, c]
одинаковы по знаку; тогда корень уравнения находится на отрезке [c, b]
и отрезок [a, c] можно исключить из дальнейшего рассмотрения, перенеся точку a в точку c: a  c; f ( a)  f (c ) (рис. 2.2, а);
б) f (a )  f (c )  0 , т. е. значение функции на концах отрезка [a, c]
противоположны по знаку; тогда корень находится на отрезке [a, c] и
отрезок [c, b] можно исключить из дальнейшего рассмотрения, перенеся
точку b в точку c: b=c (рис. 2.2, б).
Рис. 2.2
После исключения правой или левой половины отрезка продолжают деление пополам до тех пор, пока длина оставшегося интервала
[a, b] не станет меньше некоторой заданной малой величины , т. е.
b  a   , и тогда любое значение аргумента из отрезка [a, b] можно
считать корнем с погрешностью . Обычно принимают в качестве корня середину отрезка.
Отметим, что  здесь имеет смысл допустимой абсолютной погрешности вычисления корня.
Достоинством метода является его безусловная сходимость, если
на интервале [a, b] имеется хотя бы один корень. Кроме того, метод не
использует производных. К недостаткам относят медленную сходимость, т. е. достаточно большое число вычислений функции f (x ) по
сравнению с другими методами. Рекомендуется к использованию в тех
случаях, если нет жестких требований ко времени счета.
При реализации алгоритма вычисления корня алгебраического
или трансцендентного уравнения методом деления отрезка пополам
удобно оформить вычисление значения функции f (x ) (левой части
решаемого уравнения) при произвольном значении аргумента в виде
функции.