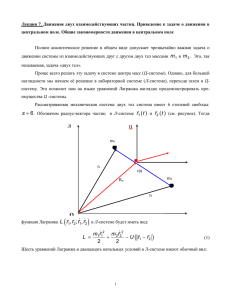
1 2 2 ik V L I U = + Ω Ω − U = M const =
реклама

ОШИБКА ЛАНДАУ Охрименко Б.А. ([email protected]) В первом томе курса теоретической физики Ландау Л.Д. и Лифшица Е.М. - «Механике» - допущена ошибка при анализе вращательного движения твердого тела. Ошибка состоит в том, что не учтена зависимость компонент тензора инерции от обобщенных координат. Обсуждаются проблемы, которые возникают при учете данной зависимости. Функция Лагранжа, определяющая движение твердого тела, приведена в [1] на стр. 127 под номером (32,4) и имеет вид L= где µV 2 1 + I ik Ωi Ω k − U , 2 2 (1) µ , V , I ik , Ωi , U - масса твердого тела, скорость движения центра масс, компоненты тензора инерции, компоненты вектора угловой скорости и потенциальная энергия, соответственно. Во втором слагаемом правой части выражения (1) предполагается суммирование по повторяющимся индексам. Первое слагаемое в (1) характеризует поступательное движение. Основной интерес представляет в (1) второе слагаемое, которое определяет характер вращательного движения твердого тела. Именно на этом слагаемом и будет сосредоточено внимание. Уравнение Лагранжа приведено на стр. 139 в виде d ∂L ∂L , (2) = dt ∂Ω ∂ϕ dϕ (стр.124). Компоненты вектора ϕ выступают в где Ω - вектор угловой скорости, Ω = dt роли обобщенных координат, а компоненты вектора Ω - в роли обобщенных скоростей. Далее (стр. 139) следуют соотношения, два из которых имеют вид ∂L = I ik Ω k = M i , ∂Ωi ∂L ∂U =− =K, ∂ϕ ∂ϕ (3) (4) где M i - компоненты вектора момента импульса. При выполнении условия U = 0 из соотношений (2, 3, 4) следует, что все компоненты момента импульса не зависят от времени, то есть M i = const . Это заключение, вообще говоря, является ошибочным. Ошибка содержится в соотношении (4), которое взято из [1] в неизменном виде с сохранением использованных обозначений, рис. 1. Это соотношение было бы справедливым, если бы значения компонент тензора инерции I ik не зависели от обобщенных координат. Однако в рассматриваемом случае ситуация иная. Рис.1. Фрагмент стр.139 из [1]. Компоненты тензора инерции I ik в случае вращательного движения твердого тела непрерывно изменяются. В частности, если в некоторый момент времени оси эллипсоида инерции ориентированы параллельно координатным осям лабораторной системы координат, то все недиагональные элементы тензора инерции оказываются в данный момент времени равными нулю. В следующий момент времени в силу продолжающегося вращательного движения указанная параллельность осей нарушается, и недиагональные элементы тензора инерции снова принимают ненулевое значение. Отмеченные обстоятельства приводят к тому, что при условии U = 0 соотношение (4) принимает вид ∂L 1 ∂I ik = Ωi Ω k . ∂ϕ 2 ∂ϕ (5) Поскольку, как было сказано выше, компоненты тензора инерции непрерывно изменяются в процессе вращательного движения твердого тела, то ∂I ik ≠ 0, ∂ϕ (6) а в силу этого на основании (5, 6) в общем случае имеем ∂L (7) ≠ 0. ∂ϕ На основании (2, 3, 7) при выполнении условия U = 0 получаем M i ≠ const . Это значит, что для такой изолированной системы как вращающееся твердое тело известный закон сохранения момента импульса не выполняется. Такой вывод зачастую воспринимается как попытка отказа от изотропного пространства. В действительности вывод о нарушении закона сохранения момента импульса не противоречит ни доказательству Эйлера, ни теореме Нётер, ни представлениям об изотропном пространстве. Доказательство Эйлера было предложено почти четверть тысячелетия тому назад. Это было время, когда научный мир лишь недавно избавился благодаря Ньютону от представлений об атомах как о частицах с крючками. Представления Эйлера о существовании только центральных сил взаимодействия между материальными точками были для того времени вполне современными. Эти представления Эйлера лежат в основе его доказательства закона сохранения момента импульса. Примерно сто лет тому назад Бьерум доказал, что между атомами в молекулах действуют не только центральные силы. Мало того, нецентральные силы взаимодействия между атомами в молекулах являются доминирующими. Это обстоятельство в настоящее время известно всем, кто в какой либо степени соприкасался с обратной спектральной задачей колебательной спектроскопии. Указанные особенности взаимодействия атомов делают несостоятельным доказательство Эйлера применительно к молекулам или твердому телу. В иных случаях, когда предположение о существовании только центральных сил является оправданным, доказательство Эйлера сохраняет свою силу. Таким образом, физические системы по отношению к доказательству Эйлера могут быть разделены на два класса. Для одного класса физических систем имеет место закон сохранения момента импульса, а для другого – нет. Из самых общих соображений следует, что в случае существования двух независимых доказательств одного и того же положения между ними должна существовать определенная корреляция. На основании этого можно ожидать, что подобное разделение физических систем должно иметь место и по отношению ко второму доказательству закона сохранения момента импульса. Второе доказательство базируется на теореме Нётер, согласно которой для физической системы имеет место закон сохранения момента импульса, если соответствующая функция Лагранжа инвариантна относительно операции инфинитезимального поворота системы координат. 2 Операция инфинитезимального поворота системы координат рассматривается как операция симметрии в пространстве. Чтобы введение такой операции в состав соответствующей группы симметрии было правомочным, необходимо полагать, что пространство является изотропным. Интуитивно такое свойство пространства представляется вполне приемлемым. Далее, как правило, следует заключение: если пространство изотропно, то функция Лагранжа должна быть инвариантной относительно рассматриваемой операции симметрии. В [1] по этому поводу говорится (стр.29) следующее: «В соответствии с этим рассмотрим бесконечно малый поворот системы и потребуем, чтобы функция Лагранжа не изменилась». Никаких иных доказательств инвариантности функции Лагранжа нет. С формальной точки зрения функция Лагранжа должна соответствовать одному из представлений группы симметрии. При этом вовсе не обязательным является условие её инвариантности по отношению к некоторой выделенной операции. Функции Лагранжа, соответствующие различным физическим системам, могут соответствовать различным представлениям группы симметрии. Не исключается и возможность инвариантности некоторых функций Лагранжа по отношению к рассматриваемой операции. По этому признаку физические системы могут быть также разделены на два класса. Для одних систем функция Лагранжа инвариантна по отношению к малому повороту системы, а для других – нет. Представляется уместной следующая аналогия. В уравнении Шредингера для атома водорода используется сферическая система координат. Поле, создаваемое ядром атома водорода, характеризуется сферической симметрией. На первый взгляд может показаться, что вследствие этого распределение плотности в электронной оболочке атома водорода обязательно должно быть сферически симметричным. В действительности, как известно, ситуация иная. У атома водорода существуют электронные оболочки как со сферически симметричным распределением плотности, так и менее симметричные. Вместо соображений общего характера об ожидаемом поведении функции Лагранжа при выполнении операции поворота системы координат на малый угол можно использовать непосредственную проверку конкретной функции (1). Будем полагать, что в (1) U = 0 и V = 0 . Функцию Лагранжа (1) можно было бы считать инвариантной относительно операции поворота на малый угол δϕ , если бы соответствующая производная равнялась нулю ∂L =0. ∂ϕ (8) Пусть в некоторый момент времени оси первой лабораторной системы координат параллельны осям эллипсоида инерции. В этом случае в первой лабораторной системе координат все недиагональные элементы тензора инерции равны нулю. Во второй лабораторной системе координат, оси которой не совпадают по направлению с осями первой системы, недиагональные элементы тензора инерции отличны от нуля. Таким образом, имеется зависимость компонент тензора инерции от ориентации системы координат и, следовательно, имеет место зависимость функции Лагранжа от угла поворота системы координат, то есть соотношение (8) не выполняется. К этому выводу можно прийти и другим путем. Как было показано выше, поворот твердого тела на малый угол вокруг мгновенной оси вращения сопровождается изменением компонент тензора инерции, что ведет к соотношению (7). Известно, что поворот твердого тела на некоторый угол в лабораторной системе координат эквивалентен повороту системы координат вокруг той же оси на такой же угол, но в противоположном направлении. Поскольку для (1) справедливо (7), то соотношение (8) не выполняется и согласно теореме Нётер закон сохранения момента импульса в данном случае также не выполняется. 1. Ландау Л.Д., Лифшиц Е.М. Механика, М.: «Наука».-1965.-204с. 3