Распространение акустической волны в подземном водопроводе

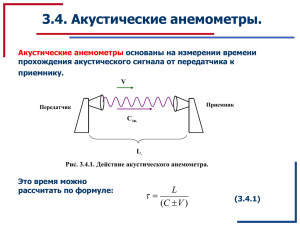
Распространение акустической волны в подземном водопроводе
А.А. Сапронов, В.А. Зибров, С.А. Тряпичкин
Современное состояние систем водоснабжения - результат многолетнего неэффективного хозяйствования. Большие материальные затраты и инфраструктурная сложность современных систем водоснабжения накладывают определенные ограничения на быструю замену
водопроводных сетей. Многофазные процессы, вызванные статическими факторами (например, транспортируемой водой по водопроводу, видом прокладки водопровода) и динамическими факторами (например, климатические условия, зоны повышенного давления) приводят к ухудшению структуры водопроводных магистралей и возрастающим количеством отказов. Очень часто механизмы, приводящие к отказам водопроводных магистралей, имеют
комплексный характер.
Области применения и недостатки существующих способов и средств мониторинга
водопроводных сетей, делают актуальной задачу разработки новых акустических регистраторов и совершенствования уже существующих приборов. Вместе с тем, имеются трудности,
обусловленные недостаточным исследованием закономерностей распространения акустических сигналов по подземным водопроводным сетям. Так, теоретически не объяснена зависимость коэффициента поглощения акустического сигнала от расстояния, не достаточно исследовано влияние грунта на характер распространения сигнала, не изучена пространственная
структура акустического поля в подземном водопроводе и возможность фильтрации отдельных мод акустического поля, не исследованы нелинейные эффекты, распространения акустических сигналов, не установлено влияние на погрешность локализации корреляционных
приборов, многомодового характера распространения акустического сигнала и дисперсии
фазовой скорости и др.
В работах [1,2] рассмотрено распространение акустической волны, распространяющейся внутри водопроводной трубы, без учета влияния грунта. Однако, когда материалом
трубы является сталь и труба не является упругой с внутренним радиусом r1 и внешним радиусом r2 , тогда акустическая волна будет распространяться через стенки трубы в грунт рис.
1. Часть переданного сигнала будет распространяться в водном потоке, а часть через стенку
трубы и грунт. В городских условиях скорость волн сдвига меняется в интервале 30…300
м/с, редко (для линий глубокого заложения) до 450м/с. Скорость распространения продольных волн в грунте меняется в пределах 600…1000м/с (для твердых грунтов до 1500м/с). Водонасыщенность грунта приводит к росту скорости продольных волн и практически не изменяет скорости поперечных волн [3]. Таким образом, в точке приёма будут присутствовать
волны, имеющие разные траектории распространения.
Поэтому без оценки влияния грунта на распространение акустической волны в подземной водопроводной трубе исследование является не полным.
Y
Расположение
источника
акустического
сигнала
Грунт
Расположение
приёмника
акустической
волны
r1
Направление
потока воды
r2
x1
x0
X
Толщина
трубы
Грунт
Z
Рис. 1 – Вид трубы погруженной в грунт
ния
Запишем передаточную функцию [4], связывающую параметры акустического давлеp и радиальной скорости v во внутренних и внешних границах трубы:
 p r2   L1 L2   p r1 
pr
vr
vr
p r2
, L2 = 2
, L3 = 2
, L4 = 2
.
 =
  , где L1 =

p r1
v r1
p r1
v r1
v r2   L3 L4  v r1 
vr1 = 0
pr1 = 0
vr1 = 0
pr1 = 0
Акустическое давление в пределах цилиндрической трубы удовлетворяет уравнению
Гельмгольца [1,2]: ~
p (γ , ω , r ) = AH 01 (ηr ) + BH 02 (ηr ) e i (γx −ωt ) , где H 01 (ηr ) – функция Ханкеля
[
]
первого рода, для волн, распространяющихся во внешнюю область; H 02 (ηr ) – функция Ханкеля второго рода, для волн, распространяющихся во внутреннюю область; A, B – коэффициенты.
iη
Тогда радиальная волновая скорость: v~ (γ , ω , r ) =
AH 1 (ηr ) + BH 2 (ηr ) e i (γx −ωt ) .
ωρ
[
1
1
p r1 
p r2 
~
~
−1
~  = M r1 ~  , где
v r2 
v r1 

 H 01 (ηr2 )
H 02 (ηr2 )
 = r21 r22  ,

и
=  iη 1
iη 2


H 1 (ηr2 )
H 1 (ηr2 ) r23 r24 

 ωρ
ωρ
[ ]
 A
Определим неизвестные коэффициенты A, B :   = M r2
B
[M ]
r1
 H 01 (ηr1 )

H 02 (ηr1 )

 = r11 r12  , M
=  iη 1
iη 2
r2


H 1 (ηr1 )
H 1 (ηr1 ) r13 r14 
 ωρ

ωρ
[ ]
]
−1
[ ]
L L 
проведем вычисление коэффициентов матрицы  1 2  :
 L3 L4 
π
π
L1 = −i ηr1 H 01 (ηr2 ) H 12 (ηr1 ) − H 02 (ηr2 ) H 11 (ηr1 ) ; L2 = ηr1 ρω H 01 (ηr2 ) H 02 (ηr1 ) − H 02 (ηr2 ) H 01 (ηr1 ) ;
4
4
π
π ηr1 1
L3 =
H 1 (ηr2 ) H 12 (ηr1 ) − H 12 (ηr2 ) H 11 (ηr1 ) ; L4 = −i ηr1 H 12 (ηr2 ) H 01 (ηr1 ) − H 11 (ηr2 ) H 02 (ηr1 ) .
4 ρω
4
Проведем расчет акустического давления, распространяемого внутри трубы, с помощью интерактивной системы MatLab. Труба водопроводная напорная из полиэтилена (ГОСТ
18599-2001, ТУ 2248-016-40270293-2002, рабочее давление 1,0МПа, диаметр 420мм, толщина 28мм). Координаты источника акустического сигнала ( r0 = 0,1r1 , x0 = 0 м); координаты
приёмника акустической волны ( r = 0,1r2 , x1 = 800 м); плотность воды 1000кг/м3; плотность
грунта 1600кг/м3; скорость звука в воде 1500м/с; скорость звука в грунте 1000м/с.
[
]
[
]
[
]
[
]
На рис. 2 приведен излучаемый ультразвуковой сигнал с частотой 55кГц и его спектр.
Временные области распространения акустического давления для заданного сигнала, приведены на рисунках (3-5).
Вид исходного сигнала
Спектр исходного сигнала
100
1
80
Амплитуда
Амплитуда
0.5
0
-0.5
60
40
20
-1
0
50
100
150
200
250 300
Время(мс)
350
400
450
0
0
500
0.2
0.4
0.6
а)
0.8
1
1.2
Частота (Гц)
1.4
1.6
1.8
2
x 10
4
б)
Рис. 2 – Заданный сигнал (а) и его спектр (б)
Область распространения давления
Область распространения давления
5000
4000
Амплитуда давления
Амплитуда давления
6000
2000
0
-2000
-4000
0
-5000
3000
-6000
3000
1.4
2000
1.4
2000
1.2
1.2
0.8
0.8
0
Время(мс)
0
Время(мс)
1
1000
1
1000
а)
б)
Рис. 3 – Временные области распространения акустического давления
мода (0,0) (а), мода (0,1) (б)
Область распространения давления
Область распространения давления
4
x 10
2
Амплитуда давления
Амплитуда давления
5000
0
1
0
-1
-2
3000
-5000
3000
1.4
2000
1.2
1
1000
1.4
2000
1.2
1
1000
0.8
0.8
Время(мс)
0
Время(мс)
0
а)
б)
Рис. 4 – Временные области распространения акустического давления
мода (1,1) (а), мода (2,2) (б)
Область распространения давления
Область распространения давления
4
5
x 10
x 10
1
Амплитуда давления
Амплитуда давления
5
0
-5
3000
0.5
0
-0.5
-1
3000
1.4
2000
1.2
1
1000
0.8
Время(мс)
0
1.4
2000
1.2
0.8
Время(мс)
а)
1
1000
0
б)
Рис. 5 – Временная область распространения акустического давления,
на приёмнике (а), в грунте (б), мода (1,263)
На рис. 3(а) приведена фундаментальная мода (0,0), которая на расстоянии 800м не
претерпевает существенных изменений. На рис. 3(б) приведена мода (0,1), где видно, что она
значительно медленнее моды (0,0), причём с увеличением расстояния форма сигнала искажается, за счет интерференции волн. Для случая (рис. 4), можно сказать, что передаваемый
ультразвуковой сигнал значительно искажен из-за результата перекрытия волн, у которых
есть более длинные пути распространения. Это признак многолучевого распространения
акустической волны в трубе, и многих ревербераций передаваемого акустического сигнала.
Необходимо отметить, что эти реверберации соответствуют более высоким модам, которые
быстрее ослабляются с увеличением расстояния.
На рис. 5 приведены временные области распространения акустического давления на
приёмнике акустической волны и грунте. Стоит отметить, что акустическая волна, прошедшая через грунт подвержена ослаблению и возбуждает больше мод, чем при распространении в трубе.
Таким образом, в цилиндрическом продуктопроводе желательно передавать информацию с помощью волны с модой (0,0). При этом следует обратить внимание на следующее:
необходимо применение согласованного фильтра для выделения режима распространения
(0,0) из принятых импульсов; большая часть энергии импульса приходится на распространение многих мод, значительно ослабляя моду (0,0).
Следовательно, для повышения надежности приёма полезного сигнала, акустическая
система связи должна содержать элементы дисперсионной компенсации, корреляционной
обработки, алгоритмы коррекции ошибок и использовать параметрические эффекты.
Литература
1. Зибров, В.А., Сапронов, А.А. Использование пьезоэлектрических преобразователей
для передачи информации о потребляемых водных ресурсах [Текст]// Энергосбережение и
водоподготовка. Научно-технический журнал, 2009 - №3. - С. 78-81.
2. Сапронов, А.А., Зибров, В.А., Занина, И.А., Соколовская, О.В.. Исследование процесса передачи информации по акустическому каналу в водопроводе [Текст]// Энергосбережение и водоподготовка. Научно-технический журнал, 2012. – №4. – С.52-54.
3. Тимошенко, В.И. Гидроакустическая энциклопедия [Текст]: Энциклопедия/ В.И
Тимошенко. – Таганрог: ТРТУ, 1999. – 788с.
4. Бреховских, Л.М., Годин, О.А. Акустика слоистых сред [Текст]: Монография.– М.:
Наука. Главная редакция физико-математической литературы, 1989. – 416с.