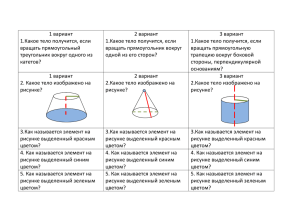
Контрольный тест № 4
реклама
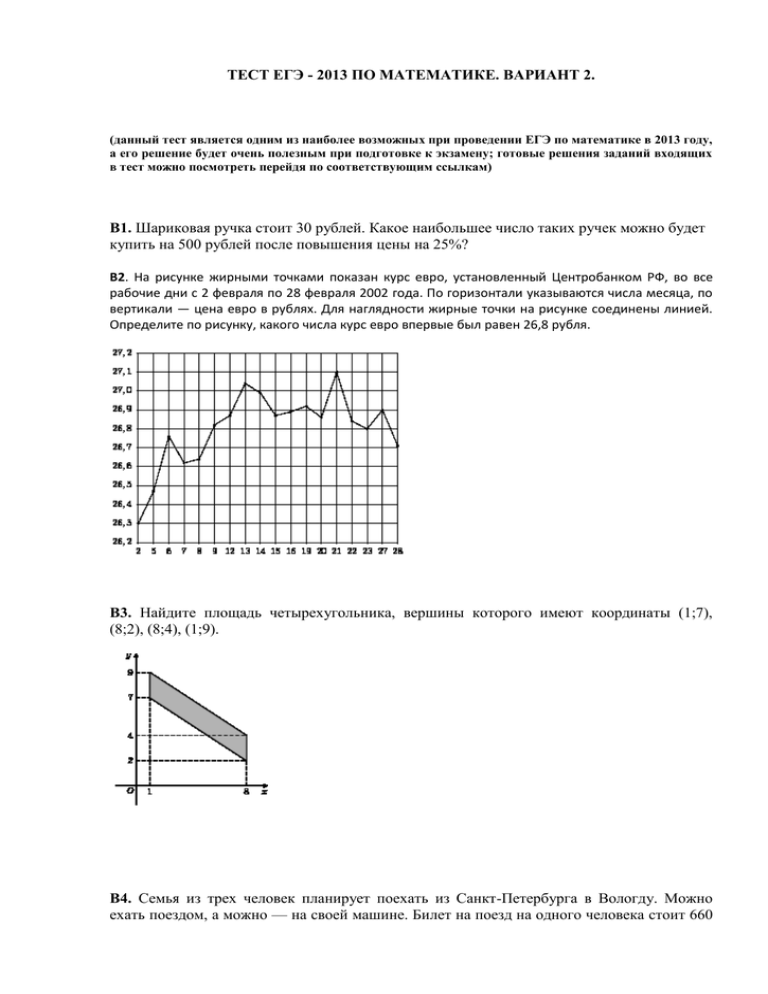
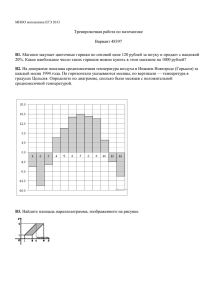
ТЕСТ ЕГЭ - 2013 ПО МАТЕМАТИКЕ. ВАРИАНТ 2. (данный тест является одним из наиболее возможных при проведении ЕГЭ по математике в 2013 году, а его решение будет очень полезным при подготовке к экзамену; готовые решения заданий входящих в тест можно посмотреть перейдя по соответствующим ссылкам) В1. Шариковая ручка стоит 30 рублей. Какое наибольшее число таких ручек можно будет купить на 500 рублей после повышения цены на 25%? В2. На рисунке жирными точками показан курс евро, установленный Центробанком РФ, во все рабочие дни с 2 февраля по 28 февраля 2002 года. По горизонтали указываются числа месяца, по вертикали — цена евро в рублях. Для наглядности жирные точки на рисунке соединены линией. Определите по рисунку, какого числа курс евро впервые был равен 26,8 рубля. В3. Найдите площадь четырехугольника, вершины которого имеют координаты (1;7), (8;2), (8;4), (1;9). В4. Семья из трех человек планирует поехать из Санкт-Петербурга в Вологду. Можно ехать поездом, а можно — на своей машине. Билет на поезд на одного человека стоит 660 рублей. Автомобиль расходует 8 литров бензина на 100 километров пути, расстояние по шоссе равно 700 км, а цена бензина равна 19,5 рубля за литр. Сколько рублей придется заплатить за наиболее дешевую поездку на троих? В5. Найдите корень уравнения . B6. Чему равна сторона правильного шестиугольника, вписанного в окружность, радиус которой равен 6? B7. Найдите значение выражения . B8. На рисунке изображен график функции Найдите сумму точек экстремума функции , определенной на интервале (-2;12) . . B9. Диаметр основания конуса равен 6, а длина образующей — 5. Найдите высоту конуса. B10. В сборнике билетов по биологии всего 55 билетов, в 11 из них встречается вопрос по ботанике. Найдите вероятность того, что в случайно выбранном на экзамене билете школьнику достанется вопрос по ботанике. B11. В цилиндрический сосуд, в котором находится 6 литров воды, опущена деталь. При этом уровень жидкости в сосуде поднялся в 1,5 раза. Чему равен объем детали? Ответ выразите в литрах. B12. Для получения на экране увеличенного изображения лампочки в лаборатории используется собирающая линза с главным фокусным расстоянием см. Расстояние от линзы до лампочки может изменяться в пределах от 30 до 50 см, а расстояние от линзы до экрана — в пределах от 150 до 180 см. Изображение на экране будет четким, если выполнено соотношение . Укажите, на каком наименьшем расстоянии от линзы можно поместить лампочку, чтобы еe изображение на экране было чeтким. Ответ выразите в сантиметрах. B13. Из городов A и B, расстояние между которыми равно 330 км, навстречу друг другу одновременно выехали два автомобиля и встретились через 3 часа на расстоянии 180 км от города B. Найдите скорость автомобиля, выехавшего из города A. Ответ дайте в км/ч. B14. Найдите точку максимума функции C1. а) Решите уравнение . . б) Найдите все корни этого уравнения, принадлежащие промежутку C2. В прямоугольном параллелепипеде заданы длины ребер . Найдите объем пирамиды если M — точка на ребре C3. Решите неравенство . , причем , , . . В треугольнике ABC высота BH делит сторону AC в отношении AH : HC = 4, а угол HBC вдвое меньше угла BAC. Биссектриса AE угла BAC пересекается с BH в точке M. Найдите отношение площади треугольника ABM к площади описанного около этого треугольника круга. C4. C5. Найдите все значения а, при каждом из которых система не имеет решений. C6. Среди обыкновенных дробей с положительными знаменателями, расположенных между числами и , найдите такую, знаменатель которой минимален.