Правила вступительного испытания по математике, проводимого университетом самостоятельно
реклама
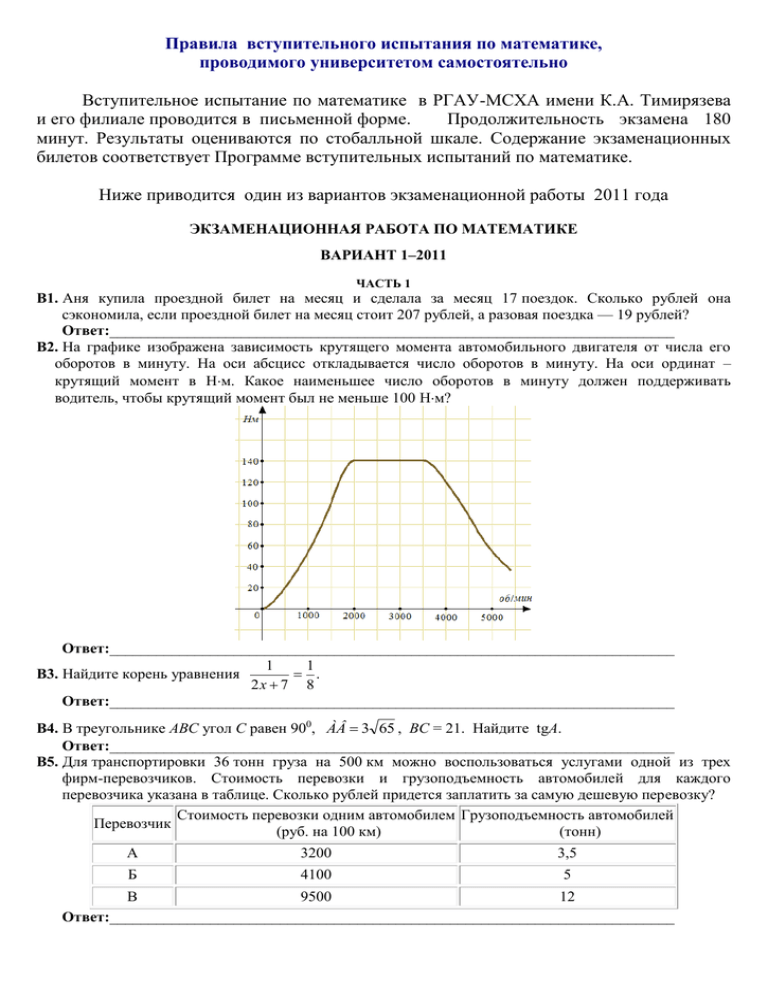
Правила вступительного испытания по математике, проводимого университетом самостоятельно Вступительное испытание по математике в РГАУ-МСХА имени К.А. Тимирязева и его филиале проводится в письменной форме. Продолжительность экзамена 180 минут. Результаты оцениваются по стобалльной шкале. Содержание экзаменационных билетов соответствует Программе вступительных испытаний по математике. Ниже приводится один из вариантов экзаменационной работы 2011 года ЭКЗАМЕНАЦИОННАЯ РАБОТА ПО МАТЕМАТИКЕ ВАРИАНТ 1–2011 ЧАСТЬ 1 В1. Аня купила проездной билет на месяц и сделала за месяц 17 поездок. Сколько рублей она сэкономила, если проездной билет на месяц стоит 207 рублей, а разовая поездка — 19 рублей? Ответ:_________________________________________________________________________ B2. На графике изображена зависимость крутящего момента автомобильного двигателя от числа его оборотов в минуту. На оси абсцисс откладывается число оборотов в минуту. На оси ординат – крутящий момент в Нм. Какое наименьшее число оборотов в минуту должен поддерживать водитель, чтобы крутящий момент был не меньше 100 Нм? Ответ:_________________________________________________________________________ 1 1 . В3. Найдите корень уравнения 2x 7 8 Ответ:_________________________________________________________________________ В4. В треугольнике ABC угол C равен 900, ÀÂ 3 65 , ВС = 21. Найдите tgA. Ответ:_________________________________________________________________________ В5. Для транспортировки 36 тонн груза на 500 км можно воспользоваться услугами одной из трех фирм-перевозчиков. Стоимость перевозки и грузоподъемность автомобилей для каждого перевозчика указана в таблице. Сколько рублей придется заплатить за самую дешевую перевозку? Стоимость перевозки одним автомобилем Грузоподъемность автомобилей Перевозчик (руб. на 100 км) (тонн) А 3200 3,5 Б 4100 5 В 9500 12 Ответ:_________________________________________________________________________ В6. Найдите площадь треугольника, изображенного на клетчатой бумаге с размером клетки 1 см 1 см. Ответ дайте в квадратных сантиметрах. Ответ:_________________________________________________________________________ 36,6 75,6 . 214,6 Ответ:_________________________________________________________________________ В7. Найдите значение выражения В8. На рисунке изображены график функции y = f(x) и касательная к нему в точке с абсциссой x0. Найдите значение производной функции f(x) в точке x0. Ответ:_________________________________________________________________________ B9. Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 9 и 3. Объем параллелепипеда равен 189. Найдите третье ребро параллелепипеда, выходящее из той же вершины. Ответ:_________________________________________________________________________ В10. Высота над землeй подброшенного вверх мяча меняется по закону h(t) = 2 + 11t – 5t2, где h — высота в метрах, t — время в секундах, прошедшее с момента броска. Сколько секунд мяч будет находиться на высоте не менее 8 метров? Ответ:_________________________________________________________________________ x3 B11. Найдите наибольшее значение функции y 1 9 x на отрезке [2; 5]. 3 Ответ:_________________________________________________________________________ B12. Среди 40000 жителей города 30% не интересуется футболом. Среди футбольных болельщиков 70% смотрело по телевизору финал Лиги чемпионов. Сколько жителей города смотрело этот матч по телевизору? Ответ:_________________________________________________________________________ ЧАСТЬ 2 С1. Решите уравнение (2 sin x 1)( cos x 1) 0. С2. В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1, все ребра которой равны 1, найдите расстояние от точки С до прямой А1В1. log 2 (2 x ) log 0,5 x 2 1. log 0,125x 8 С4. Расстояние между параллельными прямыми равно 12. На одной их них лежит точка С, а на другой – точки А и В, причем треугольник АВС – остроугольный равнобедренный и его боковая сторона равна 13. Найдите радиус окружности, вписанной в треугольник АВС. y 2 xy 4 x 9 y 20 0 y ax 1 С5. Найдите все значения параметра а, при каждом из которых система x2 С3. Решите неравенство имеет единственное решение. С6. Найдите все целые значения x и y, для которых верно равенство y2 – 1 = 32x.