Ж.Г. Ингтем, В.И. Дмитриев

УДК 550.837
Ж.Г. Ингтем1, В.И. Дмитриев1
ИСПОЛЬЗОВАНИЕ МЕТОДОВ ЧИСЛЕННОГО
ДИФФЕРЕНЦИРОВАНИЯ ДЛЯ ОБРАБОТКИ ГЕОФИЗИЧЕСКИХ
ДАННЫХ ЭЛЕКТРОМАГНИТНЫХ ЗОНДИРОВАНИЙ С ЦЕЛЬЮ
ПОВЫШЕНИЯ РАЗРЕШАЮЩЕЙ СПОСОБНОСТИ
Аннотация. Обработка данных электромагнитных зондирований не всегда позволяет провести
четкую интерпретацию полученного результата. Такая ситуация часто оказывается вызванной
близким расположением нескольких неоднородностей, или когда неоднородности расположены на
разных глубинах или неоднородности имеют разную проводимость и т.д. и т.п. Использование
дифференциальных методов электроразведки при поиске полезных ископаемых позволяет повысить
разрешающую способность методов интерпретации. Данная работа посвящена использованию метода
интегрального сплайна в обработке данных электромагнитных зондирований.
Ключевые слова: Численное дифференцирование, Интегральный сплайн, магнитотеллурическое
зондирование.
Об авторах:
1
– Московский государственный университет
Вычислительной математики и кибернетики.
имени
М.В.
Ломоносова
факультет
Целесообразность методов численного дифференцирования в обработке данных
электромагнитных зондирований обусловливается тем, что незаметные изменения
функции могут быть более четко подтверждены её производной, т.е. использование
производных позволяет выделить с хорошей точностью области, где расположена
неоднородность. Интегральный сплайн позволяет, как сглаживать геофизические
данные, полученные с погрешностью, так и одновременно вычислять производную
исследуемого процесса. Для того чтобы выделить с хорошей точностью области, где
расположена неоднородность, достаточно исследовать поведение интегрального
сплайна построенного по полученным геофизическим данным, а также поведение его
первой и второй производных. Построение интегрального сплайна заключается в
определении сплайна n -го порядка S ( x ) через производную n -го порядка P ( x ) ,
которая считается кусочно-постоянной функцией. Исходя из того, что необходимо
исследовать поведение производных до второго порядка включительно, достаточно
построить сплайн второго порядка.
Для построения интегрального сплайна решается следующая задача
 d 2S ( x)
 P( x ), x  [0, l ]

2
 dx

dS
0
 S ;
(1)
 S ( x  0)  S ;
dx
x

0

N

2
S ( x ( n ) , )  f n
 min

  n 0
~
где f n - измеренные значения в точках x ( n ) , l - длина отрезка на котором строится
сплайн, N - количество измеренных значений, P ( x ) является кусочно-постоянной
функцией на сетке построения сплайна {xk  kh} , h  l - шаг сетки, k  [0, K ] ;
K


P( x)  Pk при x  [ xk 1 , xk ] , k  [1, K ] ;   {S 0 , S , P1 , P2 , , PK } . Интегральный сплайн
S ( x ) зависит от K  2 параметров вектора  . Если количество измерений больше чем
количество параметров т.е. N  K  2 , то вектор параметров  однозначно
определяется, и, следовательно, существует единственный интегральный сплайн
аппроксимирующий заданные значения. Если N  K  2 , то  определяется
неустойчиво и требуется стабилизировать задачу минимизации с помощью
K 1
стабилизатора
( P )   ( Pk 1  Pk ) 2 . В соответствии с теорией регуляризации,
k 1
минимизация
стабилизирующего
функционала
N
K 1
2

2
min   S ( x ( n ) , )  f n      Pk 1  Pk   (где  параметр регуляризации, зависящий

 n 0

k 1
от погрешности измерения f n ) позволяет устойчиво определять вектор параметров  ,
и, следовательно, устойчиво построить интегральный сплайн S ( x ) . Первая
производная интегрального сплайна является кусочно-линейной, а вторая кусочнопостоянной. Для того, чтобы иметь гладкое представление первой и второй
производных необходимо построить интегральный сплайн по значениям этих
производных взятых в середине отрезков [ xk 1 , xk ] , k  [1, K ] .
Вычислительный эксперимент на модели МТ-полей в двумерных неоднородных
средах проводился следующим образом:
- Расчет кажущегося сопротивления для неоднородной среды при фиксированной
частоте в зависимости от x на земной поверхности;
- Внесение погрешностей в кажущееся сопротивление случайным образом;
d к
d 2к
- Вычисление
и
с помощью интегрального сплайна, и их анализ.
dx
dx 2
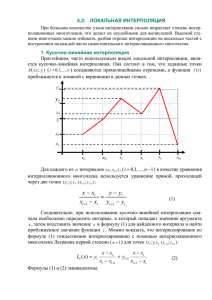
На рис. 1 приведены графики профильных кривых  k ( x ) ,  k ( x ) и  k( x ) при
1
 1024 для случая двух неоднородностей находящихся в двухслойной среде h1  1 ;
h1
1  1 ;  2  0.01 . Проводимость неоднородностей  н  10 , их глубина залегания z  2 ,
неоднородности расположены при x  [34;37.5] и x  [38.5;42] , т.е. расстояние между
неоднородностями l  1 . Погрешность в  k равна 5% от среднего аномалии  k . Из
рис.1а видно, что по  k различить аномалии от каждого тела практически невозможно
(точками показаны неточные данные). Первая производная (рис. 1б) уже разделяет
неоднородности, а вторая производная (рис.1в) даёт чёткое положение каждой
неоднородности (жирные горизонтальные отрезки обозначают расположение
неоднородностей по оси, но никак не связанны с глубиной из-за масштаба).
а)
б)
в)
Рис. 1. Пример разделения аномалий от двух тел
Полученный результат показывает эффективность применения численного
дифференцирования профильных кривых для повышения разрешающей способности
МТЗ при выделении особенностей строения среды вдоль земной поверхности.
Библиографический список
1. Дмитриев В.И., Мерщикова Н.А. Использование дифференциальных характеристик магнитного
поля при решении обратной задачи электромагнитного зондирования двумерно-неоднородных сред//
Физика Земли 1991 № 6 с. 59-64.
2. Dmitriev V.I., Dmitrieva I.V., Ingtem J.G. Integral form of the spline function in approximation
problems // Computational Mathematics and Modeling, Consultants Bureau (United States) 2013, том 24, № 4,
с. 488-497.
J.G. Ingtem, V.I. Dmitriev
USING METHODS OF NUMERICAL DIFFERENTIATION FOR
PROCESSING GEOPHYSICAL DATA ELECTROMAGNETIC SOUNDINGS FOR
THE PURPOSE OF RAISING THE RESOLUTION
Abstract. The application of differential methods in electrical prospecting of mineral resources allows to
increase the resolving power for the interpretation. This work is focused on the application of the integral form
of the spline function in the treatment of electromagnetic sounding data.
Keywords: Numerical differentiation, Integral spline, magnetotelluric sounding.