1.В цилиндрическом сосуде уровень жидкости достигает 48 см .На какой... находиться уровень жидкости, если её перелить во второй цилиндрический сосуд,...

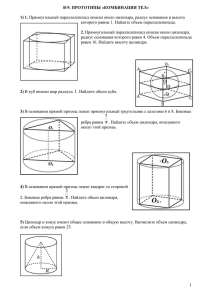
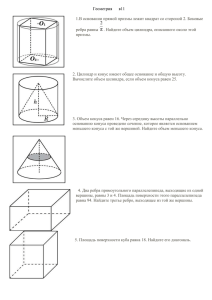
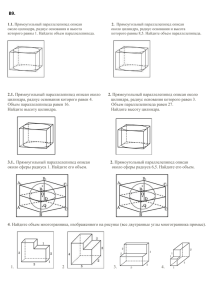
1.В цилиндрическом сосуде уровень жидкости достигает 48 см .На какой высоте будет
находиться уровень жидкости, если её перелить во второй цилиндрический сосуд, диаметр
которого в 2 раза больше диаметра первого? Ответ выразите в см.
2.Прямоугольный параллелепипед описан около цилиндра, радиус основания которого равен 5.
Объем параллелепипеда равен 50.
3. Около шара описан цилиндр, площадь поверхности которого равна 42. Найдите площадь
поверхности шара.
4. В шар вписан конус. Радиус основания конуса равен радиусу шара. Объем конуса равен 3.
Найдите объем шара
5. Найдите площадь поверхности многогранника, изображённого на
рисунке (все двугранные углы прямые).
6. Объем конуса равен 20. Через середину его высоты провели плоскость,
параллельную основанию.
Найдите объём конуса, отсекаемого этой плоскостью.
7. Найдите площадь боковой поверхности правильной шестиугольной призмы, сторона
основания которой равна 3, а высота — 6.
8. Найдите объём четырехугольной пирамиды, основанием которой является грань куба, а
вершиной — центр куба, если объём всего куба равен 15.
9. В цилиндрическом сосуде уровень жидкости достигает 18 см. На какой высоте будет
находиться уровень жидкости, если ее перелить во второй сосуд, диаметр которого в 3 раза
больше первого? Ответ дайте в сантиметрах.
10. Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).
11. Если каждое ребро куба увеличить на 1, то его объем увеличится на 19. Найдите ребро куба
12.В цилиндрический сосуд налили 2200 см3. Уровень воды при этом
достигает высоты 16 см. В жидкость полностью погрузили деталь. При этом
уровень жидкости в сосуде поднялся на 6 см. Чему равен объем детали?
Ответ выразите в см3.
13. Найдите объем многогранника, вершинами которого являются
точки A, B, A1, B1, C1 правильной треугольной призмы ABCA1B1C1, площадь основания которой
равна 7, а боковое ребро равно 9.
14. Прямоугольный параллелепипед описан около цилиндра, радиус основания которого равен
3. Объем параллелепипеда равен 18. Найдите высоту цилиндра.
15. Прямоугольный параллелепипед описан около цилиндра, радиус основания и высота
которого равны 6,5. Найдите объем параллелепипеда.
16. Прямоугольный параллелепипед описан около сферы радиуса
6. Найдите его объем.
17. В основании пирамиды лежит прямоугольник, одна боковая грань
перпендикулярна плоскости основания, а три другие боковые грани
наклонены к плоскости основания под углом 60∘.
18. Объем параллелепипеда
ABCDA1B1C1D1 равен 21. Найдите объем треугольной
пирамиды ABDA1.
19. Найдите объём правильной шестиугольной пирамиды SABCDEF, если
объем пирамиды треугольной SABC равен 39.
19. Объем параллелепипеда
ABCDA1B1C1D1 равен 1,8. Найдите объем
треугольной пирамиды AD1CB1.
20.
Объем куба равен 20. Найдите объем треугольной призмы,
отсеченной от него плоскостью, проходящей через середины двух
ребер, выходящих из одной вершины и параллельной третьему
ребру, выходящему из этой же вершины.
21. Боковое ребро правильной шестиугольной пирамиды равно 20,
сторона основания равна 10. Найдите объём пирамиды.
22. Во сколько раз уменьшится площадь боковой поверхности конуса, если радиус его
основания уменьшить в 14 раз, а длину образующей оставить прежней?
23. Найдите радиус шара, площадь поверхности которого
равна сумме площадей поверхностей шаров с радиусами 27 и
36.
24. Во сколько раз увеличится площадь поверхности октаэдра, если все
его ребра увеличить в 42 раза?
25. Во сколько раз увеличится площадь
поверхности шара, если радиус шара увеличить в
22 раза?
26. В вазу, имеющую форму правильной треугольной призмы, налили 1300 см3 воды. Ребенок
случайно уронил в вазу игрушку, полностью погрузившуюся в воду. Без игрушки уровень воды
был 20 см выше дна, после падения игрушки он поднялся на 9 см. Найдите объем игрушки.
Ответ выразите в см3.
27. Найдите объем V части цилиндра, изображенной на
рисунке. В ответе укажите Vπ.
28. Во сколько раз увеличится площадь поверхности правильного тетраэдра, если все его ребра
увеличить в 19 раз?
29. Дан куб ABCDA1B1C1D1 с ребром 6. Найдите объем многогранника, вершинами которого
являются точки A, B, C и D1
30. Площадь полной поверхности правильной четырехугольной призмы на
32 см2 больше
площади ее боковой поверхности. Найдите длину стороны основания призмы. Ответ дайте в
сантиметрах.