Российская аэрокосмическая олимпиада 2009 года Региональный комплекс интеллектуальных соревнований ИНТЕЛЛЕКТ - 2009

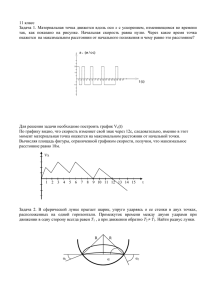
Российская аэрокосмическая олимпиада 2009 года
Региональный комплекс интеллектуальных соревнований
ИНТЕЛЛЕКТ - 2009
Место проведения: КГТУ им. А.Н. Туполева
Предмет: математика
1. Ответы на задачи 2 этапа по математике
1. (6; 1; 0), (6; –1, 0), (0; 1; 0), (0; –1; 0)
2. x  (–3; –2)  (3; +)
3. Vср  2
4.
V1  V2
V1  V2
pq
5. Задача на доказательство
6. p < 4
7. f(x) = 2x + 1
8. a  (–1; 0)  (0; 1)
9. 18
10. 20%
11. x1 
12.
7
1
  m ; x2     m ; m = 0; 1; 2; …
12
12
4 22
3
1
2. Решения задач 2-го этапа по математике
Задача 1
Поскольку k  3  0 и n 2  0 , то 6m 2  33 .
2
Так как m – целое число, то возможны три варианта:
m2 = 0, m2 = 1 и m2 = 4.
Теперь нужно рассмотреть каждый из них в отдельности, и каждый раз
получать аналогичные оценки для n2 или k  3 . Например:
2
Вариант: m2 = 0
Тогда в силу n 2  0 , получим, что k  3  11 , отсюда – следующие
2
варианты: k  3  0 , k  3  1 , k  3  4 и k  3  9 .
2
2
2
2
Подставляя (при условии, что m2 = 0) эти значения в исходное уравнение, видим, что ни одно целое значение n ему не удовлетворяет.
Варианты m2 = 1 и m2 = 4 рассматриваются аналогично.
Задача 2
ОДЗ: x  1; x  2; x  3 .
Теперь в ОДЗ неравенство можно записать так:
2
x



 0,
 2 2 log x 1 x 2  2 x  2  log x 1 1
x2  9
или
2  1x  2 x  2x 2  2 x  1
x2  9
0,
или
x  2x  12 x 2  4x 2  9  0 ,
или
 x  12  x  22  x  2 x  3 x  3  0
.

ОДЗ

Решая методом интервалов, получим: x  (–3; –2)  (3; +).
2
Задача 3
Время, затраченное на первую половину пути: t1 
пути. Вторая половина пути заняла время, равное t 2 
общее время пути: t  t1  t 2 
S
, где S – длина
2  V1
S
. Соответственно
2  V2
S 1
1  S  V  V2 
     1

2  V1 V2  2  V1  V2 
Таким образом:
Vср  2
V1  V2
.
V1  V2
Задача 4
A
Из теоремы «о хорде и касательной»
расставлены углы  и  (см. рисунок).
Тогда, если x – искомое расстояние,
то
x
p

,
BQ PB
p
q
.

PB BQ
p
Отсюда
BQ
x  p
,
PB
BQ q
 .
PB x
Таким образом, x  p 
q
или x 
x
B

pq .
P
q


x

Q
Задача 5
Поскольку x 4  2 p 4  4q 4   4 y 2 , то число x должно быть чётным. То есть
найдётся целое число n такое, что x = 2 n.
Подставив это число в уравнение, получим:

16n 4  4 y 2  2 p 4  4q 4

3
или


p 4  4q 4  2 y 4  4n 4 .
Повторяя аналогичные рассуждения для p, мы получим, что найдётся
целое m такое, что p = 2m, откуда


y 4  4n 4  2 q 4  4m 4 .
Аналогичными рассуждениями добиваемся того, что найдётся целые k,
а затем l такие, что y = 2k и q = 2l, и при этом числа n, m, k и l вновь удовлетворяют уравнению. Однако n, m, k и l – в два раза меньше, чем x, p, y и q.
Повторяя при необходимости указанный цикл рассуждений, мы получим, что
сколь угодно близко к нулю найдутся целые числа, удовлетворяющие данному уравнению. А этого быть не может!
Задача 6
Из неравенства Коши следует, что
4x 
1
1
 x  2x  2  2  4 ,
x
4
2
при этом минимальное значение левой части достигается при x=0. Таким образом, при p<4 выполнится для всех x следующее неравенство:
4x 
1
1
 x  2x  p .
x
4
2
Задача 7
Выполним замену x 
x 1
, тогда уравнение примет следующий вид:
x 1
 x 1 
 x 1 x 1
 1 f ( x )  f 


 x 1 
 x 1 x 1
или
x  1  f  x  1   2 f ( x)  x  1 .
 x 1
Подставляя левую часть в исходное уравнение, получим:
2f(x) – x – 1 – f(x) = x,
откуда вытекает, что f(x) = 2x + 1.
4
Задача 8
После замены t  2
x
 1 исходная задача примет вид: «при каких значе-
ниях параметра a уравнение
t 2  a  t 1 a2  0
не имеет корней, больших или равных 1 ?»
Поскольку дискриминант D > 0, то осталось выяснить, при каких значениях a оба корня меньше 1.
Это обеспечивается условиями:
 a
  1
 2
1  a  1  a 2  0

или a  a  0 
2
a  0
 a  (–1; 0)  (0; 1).
a   a 1   0  
a 1
Задача 9
Обозначим через S пло-
B
щадь треугольника AOB. То-
S
гда, очевидно, площадь треугольника COD также равна S,
а площадь AOD равна 2S.
По известному свойству
2
2S
A
O
C
S
D
площадей, на которые разбивается четырёхугольник (выпуклый) своими диагоналями, получаем:
S  S  2S  2
 S 2  4S  S  4 .
Таким образом, площадь трапеции 4 + 4 + 8 + 2 = 18.
Задача 10
Обозначим через C старую цену товара, через Z – затраты торговца на
его приобретение. Тогда проценты полученной прибыли имеют вид:
0,9C  Z
 100%  8%
Z

C 6
 .
Z 5
5
Обозначим через P – число процентов, на которые он рассчитывал до
снижения цены. Тогда
CZ
 100%  P %
Z
Подставляя сюда
C
   1  100%  P .
Z

C 6
 , получаем: P = 20.
Z 5
Задача 11
Расписывая произведение, стоящее в левой части уравнения, получим:
2 cos 4 x  2 sin 30 x  2 cos 4 x  1  sin 2 30 x  0 ,
откуда
2 cos 4 x  1  sin 30 x  1  2 cos 4 x  1  0 .
2
Учитывая неотрицательность слагаемых, имеем:
1

cos 4 x 
2

sin 30 x  1
или


4 x   3  2k
, k, n  Z .


30 x    2n

2
Отсюда получаем совокупность











 1

 x  12  2 k

 x     1 n

60 15
, k, n  Z .
 1

 x   12  2 k

 x     1 n

60 15
Решая первую систему совокупности, легко заметить, что k = 2m + 1,
mZ и при этом n = 15m + 9. Следовательно, первая серия решений уравнения имеет вид:
x
7
  m , m  Z .
12
6
Решение второй системы совокупности будет таким:
x

12
 m , m  Z .
Задача 12
Возводя обе части уравнения в квадрат, получим:


3x 2  4 2  2  x  1  0 .
Поскольку дискриминант уравнения положителен, то по теореме Виета:
x1  x 2 
4 22
.
3
7