Параллелограмм Трапеция
реклама
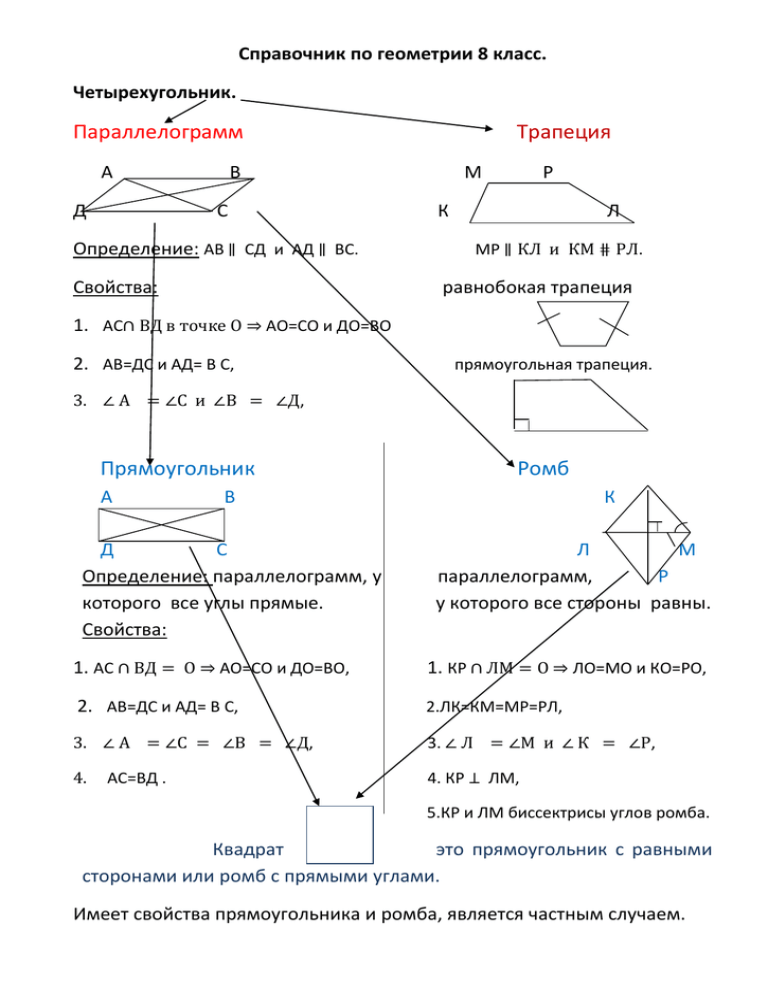
Справочник по геометрии 8 класс. Четырехугольник. Параллелограмм А Трапеция В Д С Определение: АВ ∥ СД и АД ∥ ВС. Свойства: М Р К Л МР ∥ КЛ и КМ ⋕ РЛ. равнобокая трапеция 1. АС∩ ВД в точке О ⇒ АО=СО и ДО=ВО 2. АВ=ДС и АД= В С, прямоугольная трапеция. 3. ∠ А = ∠С и ∠В = ∠Д, Прямоугольник А Ромб В К ОО Д С Определение: параллелограмм, у которого все углы прямые. Свойства: Л М параллелограмм, Р у которого все стороны равны. 1. АС ∩ ВД = О ⇒ АО=СО и ДО=ВО, 1. КР ∩ ЛМ = О ⇒ ЛО=МО и КО=РО, 2. АВ=ДС и АД= В С, 2.ЛК=КМ=МР=РЛ, 3. ∠ А = ∠С = ∠В = ∠Д, 3. ∠ Л = ∠М и ∠ К = ∠Р, 4. 4. КР ⊥ ЛМ, АС=ВД . 5.КР и ЛМ биссектрисы углов ромба. Квадрат это прямоугольник с равными сторонами или ромб с прямыми углами. Имеет свойства прямоугольника и ромба, является частным случаем. Средняя линия треугольника и трапеции. В М К А Р р А С Л В Р 𝟏 Теорема: МР∥ АС и МР = АС 𝟐 М 𝟏 Теорема: АВ∥ КЛ ∥ РМ и АВ = (КЛ + РМ) 𝟐 Прямоугольный треугольник. cos 𝛼 = А АС в А С = АВ cos 𝛼 = с cos 𝛼 = АВ с ВС а = АВ с 𝐵𝐶 𝑎 tq 𝛼 = = sin 𝛼 = в с 𝐴𝐶 С ctq 𝛼 = а ∠А = 𝜶 , ∠В = 𝜷, ∠С = 𝜸 . а +в =с 𝐴𝐶 = 𝐵𝐶 𝑏 𝑎 AC=BC ctq𝛼 = 𝑎𝑐tq𝛼 𝐴𝐶 𝑏 BC= = 𝑐𝑡𝑞𝛼 𝑐𝑡𝑞𝛼 𝐵𝐶 𝑎 cos 𝛽 = = 𝐴𝐵 𝑐 Теорема Пифагора: 𝟐 BC=AC tq𝛼 = 𝑏tq𝛼 𝐵𝐶 𝑎 AC= = 𝑡𝑞𝛼 𝑡𝑞𝛼 В 𝟐 𝑏 В С = АВ sin 𝛼 = с sin 𝛼 sin 𝛽 = tq 𝛽 = 𝟐 BC=AB cos 𝛽 = 𝑐 cos 𝛽 𝐵𝐶 𝑎 AB= = cos 𝛽 cos 𝛽 𝐴𝐶 𝑏 = 𝐴𝐵 𝑐 AC=ABsin 𝛽=csin 𝛽 𝐴𝐶 𝑏 AB= = 𝐴𝐶 AC=BC tq𝛼 = 𝑎tq𝛼 𝐴𝐶 𝑏 BC= = 𝐵𝐶 = 𝑏 𝑎 sin 𝛽 sin 𝛽 𝑡𝑞𝛼 𝑡𝑞𝛼 ctq 𝛽 = 𝐵𝐶 𝐴𝐶 = 𝑎 𝑏 BC=AC ctq𝛽 = 𝑏𝑐tq𝛽 𝐵𝐶 𝑎 AC= = 𝑐𝑡𝑞𝛽 𝑐𝑡𝑞𝛽 Основные тригонометрические тождества. tq 𝛼 = sin 𝛼 сos 𝛼 (𝐬𝐢𝐧 𝜶)𝟐 + (𝐜𝐨𝐬 𝜶)𝟐 = 𝟏 𝐬𝐢𝐧 𝜶 = 𝐜𝐨𝐬 𝜶 tq 𝛼 𝐬𝐢𝐧𝟐 𝜶 = 𝟏 − 𝐜𝐨𝐬 𝟐 𝜶 𝐜𝐨𝐬𝟐 𝜶 = 𝟏 − 𝐬𝐢𝐧𝟐 𝜶 𝐜𝐨𝐬 𝜶 = 𝐬𝐢𝐧 𝜶 tq 𝛼 𝐬𝐢𝐧 𝜶 = ±√𝟏 − 𝐜𝐨𝐬𝟐 𝜶 𝐜𝐨𝐬 𝜶 = ±√𝟏 − 𝐬𝐢𝐧𝟐 𝜶 𝟏 1+𝐭𝒒𝟐 𝜶 = 𝐜𝐨𝐬𝟐 𝜶 𝟏 1+с𝐭𝒒𝟐 𝜶 = 𝐬𝐢𝐧𝟐 𝜶 𝐬𝐢𝐧(𝟏𝟖𝟎𝟎 − 𝜶) = 𝐬𝐢𝐧 𝜶, 𝐜𝐨𝐬(𝟏𝟖𝟎𝟎 − 𝜶) = − 𝐜𝐨𝐬 𝜶, 𝒕𝒒(𝟏𝟖𝟎𝟎 − 𝜶) = −𝒕𝒒𝜶, 𝒄𝒕𝒒(𝟏𝟖𝟎𝟎 − 𝜶) = −𝒄𝒕𝒒𝜶. Таблица значений. 𝐬𝐢𝐧 𝜶 𝟎𝟎 1 𝐜𝐨𝐬 𝜶 0 tq 𝜶 - ctq 𝜶 0 𝟑𝟎𝟎 1 2 √3 2 √3 3 𝟒𝟓𝟎 √2 2 √2 2 1 √3 1 𝟔𝟎𝟎 √3 2 1 2 √3 √3 3 Декартовы координаты на плоскости. Координаты середины А(х1 ; у1 ), В(х2 ; у2 ), отрезка у А С(х; у). С С - середина АВ В х Уравнение окружности у О А х 2 у1 +у2 У= 2 2 АВ = (х1 − х2 )2 + (у1 − у2 )2 между А(х1 ; у1 ), В(х2 ; у2 ) Расстояние точками А и В х1 +х2 Х= О(а;в)-центр окружности. О А - радиус. А (х ; у) Уравнение прямой (х − а)2 + (у − в)2 = 𝑅2 а х + в у+с=0 Расположение прямой относительно системы координат. у у О х Коэффициенты: в=0, а≠ 0, 𝑐 ≠ 0 Уравнение: с ах+с=0⇒ х = - . а 0 у х 0 х Коэффициенты: Коэффициенты: а=0, в≠ 0, 𝑐 ≠ 0 а ≠ 0, в ≠ 0. с=0 Уравнение: Уравнение: с а 0x+by+c=0 ⇒ у = - . ax+by=0 ⇒ у = - х. в в Расположение прямой относительно окружности. Две точки пересечения Одна точка пересечения Нет точек пересечения у y у х х x d R> 𝑑 R< 𝑑 R=d Движение. Сохраняет расстояние при преобразовании. Центральная симметрия В А О А1 В1 АА1 ∩ В В1 = О АО=О А1 и ВО=ОВ1 АВ=А1 В1 Осевая симметрия В к В1 А Параллельный перенос В В1 А А1 В А А1 А А1 ⊥ к В В1 ⊥ к. АВ=А1 В1 поворот А1 В1 О ∠ АОА1 = ∠ВОВ1 ⃗⃗⃗⃗⃗⃗⃗ АА1 = ⃗⃗⃗⃗⃗⃗⃗ ВВ1 АА1 ⇈ ВВ1 . АВ=А1 В1 АВ=А1 В1 Векторы. Геометрическое изображение В А а⃗ ⃗⃗ в Обозначение Координаты вектора Длина вектора ⃗⃗⃗⃗⃗ АВ А(х1 у1 ), В(х2 у2 ) ⃗⃗⃗⃗⃗ АВ(х2 − х1 ; у1 − у2 ). ⃗⃗⃗⃗⃗ | |АВ = √(х2 − х1 )2 + (у1 − у2 )2 ⃗а ⇈ в ⃗ одинаково направлены. ⃗ ↑↓ с противоположно направлены, в с ⃗а ↑↓ с противоположно направлены. а⃗ = в ⃗ ⇒ а⃗ ⇈ в ⃗ и |а⃗| = |в ⃗ |. а⃗ ⃗ в Действия с векторами. действия сложение алгебраические геометрические ⃗а + в ⃗ =с а⃗(а𝟏; а𝟐 ), в ⃗ (в𝟏 ; в𝟐 ), с(а𝟏 + в𝟏 ; а𝟐 + в𝟐 ) а⃗ свойства а⃗ + в ⃗ =в ⃗ + а⃗ а⃗ + в ⃗ ⃗ в с ⃗ +с к ⃗ к Правило параллелограмма, правило треугольника. вычитание ⃗а − в ⃗ =с а⃗(а𝟏; а𝟐 ), в ⃗ (в𝟏 ; в𝟐 ), с(а𝟏 − в𝟏 ; а𝟐 − в𝟐 ) а⃗ а⃗ − в ⃗ ⃗ в а⃗ ⃗ − а⃗ в ⃗ в Умножение вектора на число 𝝀а⃗ = 𝝀(а⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗ 𝟏 ; а𝟐 ) ⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗ = (𝝀а 𝟏 ; 𝝀а𝟐 ) (λ + μ)а⃗ = λа⃗ + μа⃗ 𝜆(а⃗ + в ⃗ ) = 𝜆а⃗ + 𝜆в ⃗ 1) а⃗ 𝝀а⃗ а⃗ ⇈ 𝜆а⃗ , 𝜆 > 0, |𝝀а⃗| = |𝝀||а⃗| 2) а⃗⃗ 𝝀а⃗ а⃗ ↑↓ 𝜆а⃗ , 𝜆 < 0, Скалярное произведение векторов а⃗в ⃗ = а𝟏 в 𝟏 + а𝟐 в 𝟐 𝟐 а∗а=а ав = |а||в| 𝐜𝐨𝐬 𝝋 а⃗ ⃗ в (а⃗ + в ⃗ )с = а⃗с + в ⃗с 𝝋 а в а ⊥ в, где 𝜑 = 900 ав = 𝟎.



