План урока №_________ Тема урока:

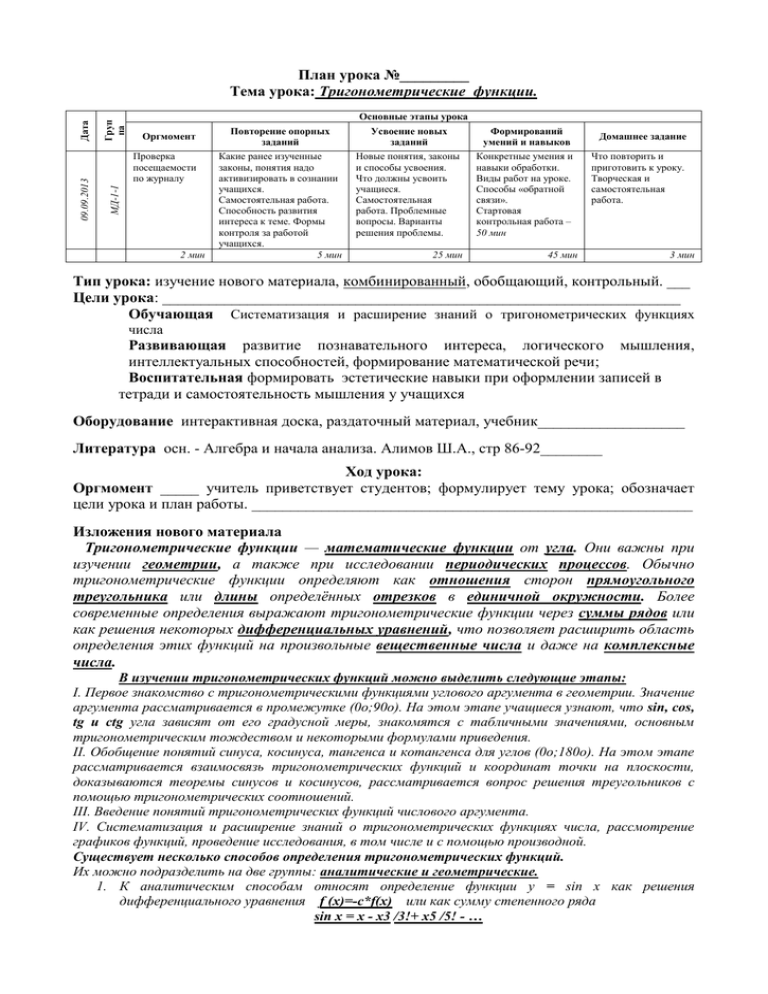
Груп
па
Основные этапы урока
Оргмомент
Проверка
посещаемости
по журналу
МД-1-1
09.09.2013
Дата
План урока №_________
Тема урока: Тригонометрические функции.
2 мин
Повторение опорных
заданий
Усвоение новых
заданий
Формирований
умений и навыков
Какие ранее изученные
законы, понятия надо
активизировать в сознании
учащихся.
Самостоятельная работа.
Способность развития
интереса к теме. Формы
контроля за работой
учащихся.
5 мин
Новые понятия, законы
и способы усвоения.
Что должны усвоить
учащиеся.
Самостоятельная
работа. Проблемные
вопросы. Варианты
решения проблемы.
Конкретные умения и
навыки обработки.
Виды работ на уроке.
Способы «обратной
связи».
Стартовая
контрольная работа –
50 мин
25 мин
Домашнее задание
Что повторить и
приготовить к уроку.
Творческая и
самостоятельная
работа.
45 мин
3 мин
Тип урока: изучение нового материала, комбинированный, обобщающий, контрольный. ___
Цели урока: ___________________________________________________________________
Обучающая Систематизация и расширение знаний о тригонометрических функциях
числа
Развивающая развитие познавательного интереса, логического мышления,
интеллектуальных способностей, формирование математической речи;
Воспитательная формировать эстетические навыки при оформлении записей в
тетради и самостоятельность мышления у учащихся
Оборудование интерактивная доска, раздаточный материал, учебник___________________
Литература осн. - Алгебра и начала анализа. Алимов Ш.А., стр 86-92________
Ход урока:
Оргмомент _____ учитель приветствует студентов; формулирует тему урока; обозначает
цели урока и план работы. _________________________________________________________
Изложения нового материала
Тригонометрические функции — математические функции от угла. Они важны при
изучении геометрии, а также при исследовании периодических процессов. Обычно
тригонометрические функции определяют как отношения сторон прямоугольного
треугольника или длины определённых отрезков в единичной окружности. Более
современные определения выражают тригонометрические функции через суммы рядов или
как решения некоторых дифференциальных уравнений, что позволяет расширить область
определения этих функций на произвольные вещественные числа и даже на комплексные
числа.
В изучении тригонометрических функций можно выделить следующие этапы:
I. Первое знакомство с тригонометрическими функциями углового аргумента в геометрии. Значение
аргумента рассматривается в промежутке (0о;90о). На этом этапе учащиеся узнают, что sin, сos,
tg и ctg угла зависят от его градусной меры, знакомятся с табличными значениями, основным
тригонометрическим тождеством и некоторыми формулами приведения.
II. Обобщение понятий синуса, косинуса, тангенса и котангенса для углов (0о;180о). На этом этапе
рассматривается взаимосвязь тригонометрических функций и координат точки на плоскости,
доказываются теоремы синусов и косинусов, рассматривается вопрос решения треугольников с
помощью тригонометрических соотношений.
III. Введение понятий тригонометрических функций числового аргумента.
IV. Систематизация и расширение знаний о тригонометрических функциях числа, рассмотрение
графиков функций, проведение исследования, в том числе и с помощью производной.
Существует несколько способов определения тригонометрических функций.
Их можно подразделить на две группы: аналитические и геометрические.
1. К аналитическим способам относят определение функции у = sin х как решения
дифференциального уравнения f (х)=-c*f(х) или как сумму степенного ряда
sin х = х - х3 /3!+ х5 /5! - …
2. К геометрическим способам относят определение тригонометрических функций на основе
проекций и координат радиус-вектора, определение через соотношения сторон прямоугольного
треугольника и определения с помощью числовой окружности. В школьном курсе предпочтение
отдается геометрическим способам в силу их простоты и наглядности.
 Синусом угла х называется ордината
точки, полученной поворотом точки
(1; 0) вокруг начала координат на угол
х (обозначается sin x).
Область определения х € (-∞;∞)
Область значений у € [-1; 1]
Ограниченность: ограничена
Четность: sin(-x) = - sinx
Периодичность: Т = 2π
 Косинусом угла х называется абсцисса
точки, полученной поворотом точки
(1; 0) вокруг начала координат на угол
х (обозначается cos x).
Область определения х € (-∞;∞)
Область значений у € [-1; 1]
Ограниченность: ограничена
Четность: cos(-x) = cosx
Периодичность: Т = 2π
 Тангенсом
угла
х
называется
отношение синуса угла х к косинусу
угла х.
Область определения х ≠ (π/2+πn)
Область значений у € (-∞;∞)
Ограниченность: не ограничена
Четность: tg(-x) = - tgx
Периодичность: Т = π
 Котангенсом угла х называется
отношение косинуса угла х к синусу
угла х
Область определения х ≠ πn
Область значений у € (-∞;∞)
Ограниченность: не ограничена
Четность:ctg(-x) = - ctgx
Периодичность: Т = π
Закрепление: работа с учебником - стр91, №325-326
Домашнее задание: Алимов, стр. 92, №329___________________________________
Преподаватель ___________________________ (_________Л.Н.Калайдарова_________)