Диагностическая контрольная работа для 11 класса 1 вариант Январь 2010 года

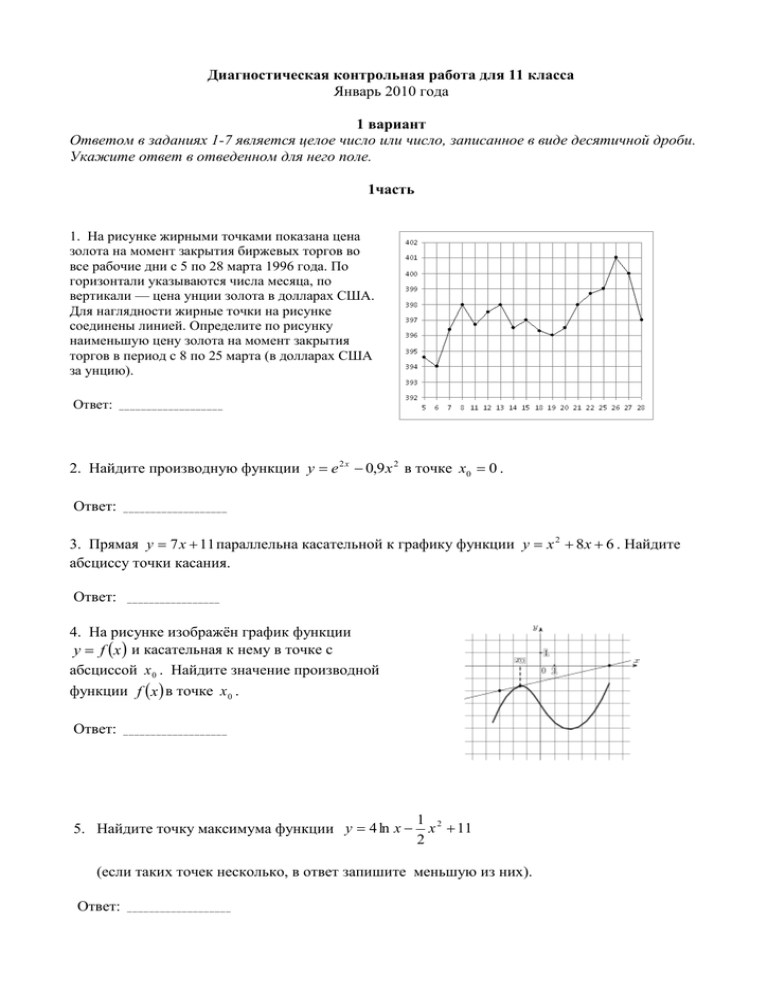
Диагностическая контрольная работа для 11 класса
Январь 2010 года
1 вариант
Ответом в заданиях 1-7 является целое число или число, записанное в виде десятичной дроби.
Укажите ответ в отведенном для него поле.
1часть
1. На рисунке жирными точками показана цена
золота на момент закрытия биржевых торгов во
все рабочие дни с 5 по 28 марта 1996 года. По
горизонтали указываются числа месяца, по
вертикали — цена унции золота в долларах США.
Для наглядности жирные точки на рисунке
соединены линией. Определите по рисунку
наименьшую цену золота на момент закрытия
торгов в период с 8 по 25 марта (в долларах США
за унцию).
Ответ:

2. Найдите производную функции y  e 2 x  0,9 x 2 в точке x0  0 .
Ответ:

3. Прямая y  7 x  11 параллельна касательной к графику функции y  x 2  8x  6 . Найдите
абсциссу точки касания.
Ответ:

4. На рисунке изображён график функции
y  f x  и касательная к нему в точке с
абсциссой x 0 . Найдите значение производной
функции f x  в точке x 0 .
Ответ:

5. Найдите точку максимума функции y  4 ln x 
1 2
x  11
2
(если таких точек несколько, в ответ запишите меньшую из них).
Ответ:

 3 
;0 .
6. Найдите наибольшее значение функции y  6 cos x  14 x  5 на отрезке 
 2 
Ответ:

7. Прямоугольный параллелепипед описан около сферы радиуса 0,5. Найдите его объем.
Ответ:

2 часть
8. Сколько корней имеет уравнение log 3 x  6 log 3 x  a в зависимости от a?
3
2
9. Радиус основания цилиндра равен 1, а высота равна 2 6 . Отрезки AB и CDдиаметры одного из оснований цилиндра, а отрезок AA1 - его образующая. Известно, что
AD  3 . Найдите косинус угла между прямыми А1С и BD.
2 вариант
Ответом в заданиях 1-7 является целое число или число, записанное в виде десятичной дроби.
Укажите ответ в отведенном для него поле
1часть
1. На рисунке жирными точками показана
цена золота на момент закрытия биржевых
торгов во все рабочие дни с 3 по 24 октября
2002 года. По горизонтали указываются числа
месяца, по вертикали — цена унции золота в
долларах США. Для наглядности жирные
точки на рисунке соединены линией.
Определите по рисунку наибольшую цену
золота на момент закрытия торгов в период с
15 по 23 октября (в долларах США за унцию).
Ответ:

2. Найдите производную функции y  e 3 x  3x 2 в точке x0  0.
Ответ:

3. Прямая y  3x  6 параллельна касательной к графику функции y  x 2  5 x  8 . Найдите
абсциссу точки касания.
Ответ:

4. На рисунке изображён график функции
y  f x  и касательная к нему в точке с
абсциссой x 0 . Найдите значение производной
функции f x  в точке x 0 .
Ответ:

5. Найдите точку минимума функции y  9 ln x 
1 2
x 3
2
(если таких точек несколько, в ответ запишите меньшую из них).
Ответ:

  
6. Найдите наибольшее значение функции y  17 x  5 sin x  7 на отрезке  ; 0.
 2 
Ответ: 
7. Прямоугольный параллелепипед описан около цилиндра, радиус основания и высота
которого равны 1. Найдите объем параллелепипеда.
Ответ:

2часть
8. Сколько корней имеет уравнение log 2 x  12 log 2 x  a в зависимости от a?
3
9. Диаметр и хорда AB основания конуса равны 26 и 24, а тангенс угла наклона образующей
12
. Найдите тангенс угла между плоскостью основания конуса и
к плоскости основания равен
13
плоскостью сечения, проходящего через вершину конуса и хорду AB.
Ответы к заданиям диагностической контрольной работы
Вариант 1
№
задания
Ответ
1
2
3
4
5
6
7
396
2
-0,5
0,25
2
1
1
№8. при a  32; a  0 - 1 корень, при a  32; a  0 - 2 корня, при  32  a  0 - 3 корня
№9. 0,2
Вариант 2
№
задания
Ответ
1
2
3
4
5
6
7
315
3
4
0,75
3
7
4
№8. при a  16; a  16 - 1 корень, при a  16; a  16 - 2 корня, при  16  a  16 - 3 корня
№9. 2,4
Пояснительная записка
по проведению диагностической контрольной работы
в 11 классах в январе 2010 года
Цель работы: получение информации об усвоении учащимися материала 11 класса.
Данная работа проводится 27-29 января в 11 классе.
Работа состоит из двух частей и содержит 9 заданий.
Первая часть работы содержит 7 заданий базового уровня. К этим заданиям необходимо дать
краткий ответ, записанный в отведенном для этого поле в виде целого числа или десятичной
дроби.
Вторая часть содержит 2 задания повышенного уровня. При их выполнении необходимо
записать обоснованное решение.
На выполнение всей работы дается 100 минут (два урока).
В течение первых 5 минут первого урока предполагается инструктаж учеников.
За выполнение работы рекомендуется выставлять две оценки: аттестационная отметка и
тестовый балл.
За каждое верно решенное задание первой части начисляется 1 тестовый балл.
За каждое задание второй части можно получить до 2 тестовых баллов.
Таким образом, максимально возможное число тестовых баллов за всю работу равно 11.
Рекомендуемые критерии перевода тестового балла в аттестационную отметку:
Тестовый балл
3-5
6– 8
9 – 11
Аттестационная отметка
«3»
«4»
«5»
Критерии оценки выполнения заданий второй части работы:
Количество
Критерии оценки заданий № 8 и № 9
баллов
Обоснованно получен верный ответ.
2

1
1) Ход решения верный. Получен верный ответ, но имеется ошибка в
обосновании, не повлиявшая на ответ.
2) Ход решения верный. Приведены верные обоснования, но допущена
ошибка, в результате которой получен неверный ответ.
0
Решение не соответствует ни одному из критериев, перечисленных выше.
2
Максимальный балл
Рекомендуется собрать черновики учащихся, чтобы убедиться, что учащиеся решали задачи самостоятельно, и
проанализировать их основные ошибки.
№
задания
Проверяемые элементы
Максимальный
балл
Примерное
время
выполнения
( в минутах)
Базовый
1
2
Базовый
1
3
1
5
Базовый
1
5
Базовый
1
10
Базовый
1
10
Базовый
1
10
Повышенный
2
20
Повышенный
2
20
Уровень
сложности
задания
Часть 1
1
2
3
4
5
6
7
Уметь использовать
приобретенные знания и
умения в практической
деятельности и
повседневной жизни
Уметь вычислять значение
производной в заданной
точке
Уметь применять
геометрический смысл
производной
Уметь исследовать функцию
по графику
Уметь выполнять действия с
функциями
Уметь выполнять действия с
функциями
Уметь выполнять действия с
геометрическими фигурами
Базовый
Часть 2
8
9
Уметь строить и исследовать
простейшие математические
модели
Уметь выполнять действия с
геометрическими фигурами
Анализ диагностической контрольной работы по математике в 11 классах
Январь 2010 г.
1. ОУ № _________
2. Общее по ОУ количество учащихся, выполнявших работу: ____________
3. Общее по ОУ количество: «5» ________ уч-ся __________ %
«4» ________ уч-ся __________ %
«3» ________ уч-ся __________ %
«2» ________ уч-ся __________ %
4. Количество учащихся, выполнивших верно все 9 заданий: _______ уч-ся _________ %
5. Анализ выполнения заданий (общая информация по ОУ):
№ задания
% верно
выполнивших

1
2
3
4
5
6
7
8
9
Верно выполнившими задания № 8 и № 9 считаются те, кто получил за них 2 балла.
6. Анализ результатов диагностической работы просим направить по электронной почте на
адрес НМЦ для методиста по математике Федорчук О.Ф. до 04 февраля 2010 г.
Желаем успеха!!!