исследованию функций»
реклама

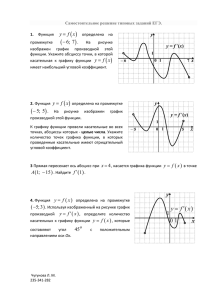
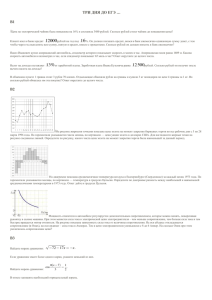
Конспект открытого урока Обобщающий урок по теме: «Применение производной к исследованию функций» Цель урока: обобщить и систематизировать знания учащихся по данной теме: нахождения промежутков монотонности, точек экстремума , нахождение наибольшего и наименьшего значения функции на концах отрезка; подготовка к ЕГЭ развитие математической речи, логического мышления, сообразительности, внимательности. воспитание трудолюбия, аккуратности. Эпиграфом нашего урока будет высказывание Конфуция Эпиграф: Три пути ведут к знанию: путь размышления – это путь самый благородный, путь подражания – это путь самый легкий и путь опыта – это путь самый горький. То есть на уроке мы будем размышлять, подражать, т.е. делать по образцу и набираться опыта. Начнём урок с разминки Знак производной меняется по схеме, изображённой на рисунке • Найдите промежутки возрастания и убывания функции • Как называются промежутки возрастания и убывания • Промежутки монотонности • Найдите,точки максимума и точки минимума • Как называются точки максимума и минимума • Точки экстремума • На рисунке изображён график производной функции у=f‘(x), заданной на отрезке [а;b]. Определите число промежутков убывания На рисунке изображен график у = f'(х) — производной функции f(х), определенной на интервале (-6; 12). Найдите промежутки возрастания функции f(х). В ответе укажите длину наибольшего из них. На рисунке изображен график у = f' (х) — производной функции f(х), определенной на интервале (-16; 7). Найдите количество точек экстремума функции f(х), принадлежащих отрезку [-15; 6]. На рисунке изображен график у =f' (х) — производной функции f(х), определенной на интервале (-2; 10). Найдите точку экстремума функции f(х) на интервале (—1; 9). На рисунке изображен график функции f(х) и семь точек на оси абсцисс: х1, х2, х3, ... х7. В скольких из этих точек производная функции f(х) положительна? На рисунке изображен график функции f(х) и одиннадцать точек на оси абсцисс: х1, х2, х3, ... х11. В скольких из этих точек производная функции f(х) отрицательна? Функция у =f(x) определена на отрезке [-2; 3]. На рисунке изображен график производной функции у =f'(х). В какой точке отрезка функция принимает наименьшее значение? Функция у =f(x) определена на отрезке [-4; 2]. На рисунке изображен график производной функции у =f'(х). В какой точке отрезка функция принимает наименьшее значение? Наши ошибки. • На рисунке изображён график производной. Определяя точки минимума, ученик указал точку х = 2. Прав ли он? • На рисунке изображён график производной. Определяя точки минимума, ученик указал точки х = -4, х =1, х = 3. Прав ли он? На рисунке изображён график производной. Определяя промежутки возрастания, ученик указал 3 промежутка. Прав ли он? Тест Ответы: Вариант 1 1) 3 2) 2 3) -1 Вариант 2 1) 1 2) 3 3) 2 Исторические сведения • Математика развивалась стремительно, но без понятия производной многие исследования не имели смысла. В 1679 году Пьер Ферма находил экстремумы функции, касательные, наибольшие и наименьшие значения функций. Но в своих записях он использовал сложнейшую символику Виета, и поэтому эти исследования не привели к созданию теории дифференциальных исчислений. В 1736 году Исаак Ньютон получил теорию дифференциальных исчислений методом флюксий (производных). Но вся теория была осмыслена с точки зрения физики. Математики хотели строгих логических обоснований. Современник Ньютона Лейбниц предложил новый подход к математическому анализу. Он ввёл обозначения дифференциала, функции, такие понятия как ордината, абсцисса, координата. Но в его теории было много “тёмных мест”. И вот в 18 веке величайший математик Леонард Эйлер создал теорию дифференциальных исчислений, и в таком виде она изучается и по сей день. Письменные тренировочные задания из КИМов № 1 (В8) Найдите точку максимума функции у=ех-1 х² Вспомнить алгоритм № 2 (В14) Найдите наименьшее значение функции у=х³-27х+11 на отрезке [0;4] Проверочная работа Вариант 1 № 1. Найдите точку максимума функции у = х3-6х2-15х+4 № 2. Найдите наименьшее значение функции у = х3-3х+16 на отрезке [-3; 0] Вариант 2 № 1. Найдите точку минимума функции у = 2х3-15х2+24х-1 № 2. Найдите наибольшее значение функции у = х3-3х+19 на отрезке [-2; 0] Ответы: Вариант 1 1) -1 2) 3 Вариант 2 1) 4 2) 21 Подведение итогов. Выставление оценок. Материал этого урока поможет вам успешно выполнить задания при итоговой аттестации. Все задания урока были составленны по образцам контрольно измерительных материалов 2010-2011 года единого государственного экзамена и нового проэкта демонстрационного варианта 2012 г. Домашнее задание. Составить тест (из пяти заданий по теме: "Производная"). Рефлексия. Я хочу вам пожелать, чтобы у вас была только положительная производная, чтобы знания ваши только возрастали. Спасибо за урок.