алгебре и началам анализа
реклама
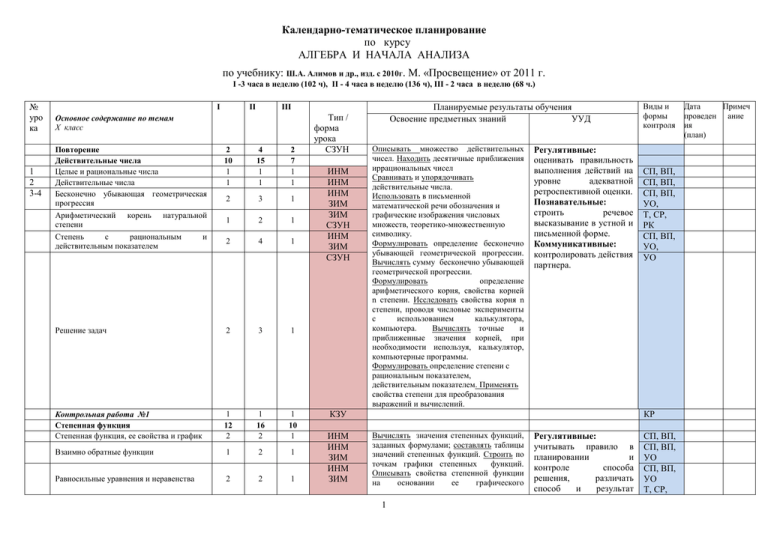
Календарно-тематическое планирование по курсу АЛГЕБРА И НАЧАЛА АНАЛИЗА по учебнику: Ш.А. Алимов и др., изд. с 2010г. М. «Просвещение» от 2011 г. I -3 часа в неделю (102 ч), II - 4 часа в неделю (136 ч), III - 2 часа в неделю (68 ч.) № уро ка 1 2 3-4 I II Планируемые результаты обучения Освоение предметных знаний УУД III Основное содержание по темам X класс Повторение Действительные числа Целые и рациональные числа Действительные числа Бесконечно убывающая геометрическая прогрессия Арифметический корень натуральной степени Степень с рациональным и действительным показателем 2 10 1 1 4 15 1 1 2 7 1 1 2 3 1 1 2 1 2 4 1 Решение задач 2 3 1 Контрольная работа №1 Степенная функция Степенная функция, ее свойства и график 1 12 2 1 16 2 1 10 1 Взаимно обратные функции 1 2 1 Равносильные уравнения и неравенства 2 2 1 Тип / форма урока СЗУН ИНМ ИНМ ИНМ ЗИМ ЗИМ СЗУН ИНМ ЗИМ СЗУН Описывать множество действительных чисел. Находить десятичные приближения иррациональных чисел Сравнивать и упорядочивать действительные числа. Использовать в письменной математической речи обозначения и графические изображения числовых множеств, теоретико-множественную символику. Формулировать определение бесконечно убывающей геометрической прогрессии. Вычислять сумму бесконечно убывающей геометрической прогрессии. Формулировать определение арифметического корня, свойства корней n степени. Исследовать свойства корня n степени, проводя числовые эксперименты с использованием калькулятора, компьютера. Вычислять точные и приближенные значения корней, при необходимости используя, калькулятор, компьютерные программы. Формулировать определение степени с рациональным показателем, действительным показателем. Применять свойства степени для преобразования выражений и вычислений. Регулятивные: оценивать правильность выполнения действий на уровне адекватной ретроспективной оценки. Познавательные: строить речевое высказывание в устной и письменной форме. Коммуникативные: контролировать действия партнера. КЗУ ИНМ ИНМ ЗИМ ИНМ ЗИМ Виды и формы контроля СП, ВП, СП, ВП, СП, ВП, УО, Т, СР, РК СП, ВП, УО, УО КР Вычислять значения степенных функций, заданных формулами; составлять таблицы значений степенных функций. Строить по точкам графики степенных функций. Описывать свойства степенной функции на основании ее графического 1 Регулятивные: учитывать правило в планировании и контроле способа решения, различать способ и результат СП, ВП, СП, ВП, УО СП, ВП, УО Т, СР, Дата Примеч проведен ание ия (план) Иррациональные уравнения 3 3 3 Иррациональные неравенства 2 3 2 Решение задач 1 3 1 Контрольная работа №2 1 1 1 Показательная функция 9 12 2 2 1 Показательные уравнения, неравенства и их системы 5 5 4 уравнений и 1 3 1 представления. Моделировать реальные зависимости с помощью формул и графиков степенных функций. Интерпретировать графики реальных зависимостей. Использовать компьютерные программы для исследования положения на координатной плоскости графиков степенных функций в зависимости от значений коэффициентов, входящих в формулу. Распознавать виды степенных функций. Строить более сложные графики на основе графиков степенных функций; описывать их свойства Применять понятие равносильности для решения уравнений и неравенств. Решать иррациональные уравнения и иррациональные неравенства. Применять метод интервалов для решения иррациональных неравенств. Использовать функциональнографические представления для решения и исследования иррациональных уравнений, неравенств, систем уравнений и неравенств. Использовать готовые компьютерные программы для поиска пути решения и иллюстрации решения уравнений и неравенств действия. Познавательные: ориентироваться в разнообразии способов решения задач. Коммуникативные: учитывать разные мнения и стремиться к координации различных позиций в сотрудничестве, контролировать действия партнера КЗУ 7 Показательная функция, ее свойства и график Система показательных неравенств ИНМ ЗИМ ИНМ ЗИМ ИНМ ИНМ ЗИМ СЗУН ИНМ ЗИМ Вычислять значения показательных функций, заданных формулами; составлять таблицы значений показательных функций. Строить по точкам графики показательных функций. Описывать свойства показательной функции на основании ее графического представления. Моделировать реальные зависимости с помощью формул и графиков. Интерпретировать графики реальных зависимостей. Использовать компьютерные программы для исследования положения на координатной плоскости графиков показательных функций в зависимости от значений коэффициентов, входящих в формулу. Распознавать виды показательных функций. Строить более сложные графики на основе графиков показательных функций; описывать их свойства. 2 РК УО РК КР СП, ВП, УО Регулятивные: различать способ и результат действия. Познавательные: владеть общим приемом решения задачи. Коммуникативные: договариваться и приходить к общему решению в совместной деятельности, в том числе в ситуации столкновения интересов. Т, СР, РК СП, ВП, УО СП, ВП, УО СП, ВП, УО Контрольная работа №3 Логарифмическая функция 1 1 1 18 23 11 КЗУ ИНМ ЗИМ Определение логарифма 2 Свойства логарифмов 3 2 3 1 1 Десятичные и натуральные логарифмы 2 2 1 Решение задач 1 4 1 Контрольная работа №4 1 1 1 Логарифмическая функция, ее свойства и график Логарифмические неравенства уравнения и 2 6 3 7 1 4 ЗИМ СЗУН ЗИМ СЗУН КЗУ ИНМ ЗИМ ИНМ ЗИМ СЗУН КЗУ Контрольная работа №5 Тригонометрические формулы 1 1 1 20 22 12 Формулировать определение логарифма, свойства логарифма. Вычислять значения логарифмических функций, заданных формулами; составлять таблицы значений логарифмических функций. Строить по точкам графики логарифмических функций. Описывать свойства логарифмической функции на основании ее графического представления. Моделировать реальные зависимости с помощью формул и графиков. Интерпретировать графики реальных зависимостей. Использовать компьютерные программы для исследования положения на координатной плоскости графиков логарифмических функций в зависимости от значений коэффициентов, входящих в формулу. Распознавать виды логарифмических функций. Строить более сложные графики на основе графиков логарифмических функций; описывать их свойства. Решать логарифмические уравнения и системы уравнений. Решать логарифмические неравенства. Применять метод интервалов для решения логарифмических неравенств. Конструировать эквивалентные речевые высказывания с использованием алгебраического и геометрического языков. Использовать функциональнографические представления для решения и исследования логарифмических уравнений, неравенств, систем уравнений и неравенств. Использовать готовые компьютерные программы для поиска пути решения и иллюстрации решения уравнений и неравенств. Регулятивные: вносить необходимые коррективы в действие после его завершения на основе учета характера сделанных ошибок. Познавательные: проводить сравнение, сериацию и классификацию по заданным критериям. Коммуникативные: учитывать разные мнения и стремиться к координации различных позиций в сотрудничестве Регулятивные: учитывать правило в планировании и контроле способа решения, различать способ и результат действия. Познавательные: ориентироваться на разнообразие способов решения задач. Коммуникативные: учитывать разные мнения и стремиться к координации различных позиций в сотрудничестве, контролировать действия партнера. Регулятивные: 3 КР СП, ВП, УО Т, СР, РК СП, ВП, УО Т, СР, РК СП, ВП, УО Т, СР, РК СП, ВП, УО Т, СР, РК Т, СР, РК КР ВП, УО Т, СР, РК СП, ВП, УО Т, СР, РК КР СП, ВП, УО Радианная мера угла и дуги 1 1 1 Поворот точки вокруг начала координат Определение синуса, косинуса и тангенса угла Знаки тригонометрических функций 1 1 1 2 2 1 1 1 1 Зависимость между синусом, косинусом и тангенсом одного и того же угла 2 2 1 ЗИМ СЗУН СЗУН КЗУ ИНМ ЗИМ ИНМ Тригонометрические тождества Синус, косинус и тангенс углов 1 и Формулы сложения 1 3 1 1 3 1 1 1 Синус, косинус и тангенс двойного угла 1 2 1 Синус, косинус и тангенс половинного угла* 1 1 - Формулы приведения 1 2 1 Сумма и разность синусов. Сумма и разность косинусов. 2 2 1 Формулировать определение и иллюстрировать понятие синуса, косинуса, тангенса и котангенса на единичной окружности. Объяснять и иллюстрировать на единичной окружности знаки тригонометрических функций. Формулировать и разъяснять основное тригонометрическое тождество. Вычислять значения тригонометрической функции угла по одной из его заданных тригонометрических функций. Выводить формулы сложения. Выводить формулы приведения. Выводить формулы суммы и разности синусов, косинусов. Применять тригонометрические формулы для преобразования тригонометрических выражений. ИНМ ЗИМ ИНМ ЗИМ ИНМ ЗИМ ИНМ ЗИМ ИНМ ЗИМ СЗУН Решение задач 2 2 1 Контрольная работа №6 1 1 1 осуществлять итоговый и пошаговый контроль по результату. Познавательные: строить речевые высказывания в устной и письменной форме. Коммуникативные: учитывать разные мнения и стремиться к координации различных позиций в сотрудничестве. Т, СР, РК ВП, УО Т, СР, РК СР, РК КР СП, ВП, УО Т, СР, РК СП, ВП, УО Т, СР, РК СП, ВП, УО Т, СР, РК СП, ВП, УО Т, СР, РК СП, ВП, УО Т, СР, РК СП, ВП, УО Т, СР, РК СП, ВП, УО Т, СР, РК СП, ВП,РК СП, ВП, УО Т, СР, РК КР КЗУ 4 Тригонометрические уравнения и неравенства 20 25 11 СЗУН Уравнение cos x a . 2 2 1 Уравнение Уравнения sin x a . tgx a . 2 2 1 2 2 1 3 4 2 Решение простейших тригонометрических уравнений Контрольная работа №7 1 Решение тригонометрических уравнений Примеры решения простейших тригонометрических неравенств* 5 3 1 7 4 1 3 - Решение задач 1 2 1 Контрольная работа №8 Тригонометрические функции** Область определения и множество значений тригонометрических функций Чётность, нечётность, периодичность тригонометрических функций 1 10 1 12 1 7 1 2 1 3 3 1 Функция график y cos x, ее свойства и Функция график y sin x, ее свойства и Функции y tgx, свойства и графики y ctgx их 1 1 1 1 1 1 ИНМ 1 1 1 ИНМ ЗИМ ИНМ ЗИМ Проводить доказательное рассуждение о корнях простейших тригонометрических уравнений. Решать тригонометрические уравнения и простейшие неравенства. Применять тригонометрические формулы для решения тригонометрических уравнений. Использовать различные методы для решения тригонометрических уравнений. Конструировать эквивалентные речевые высказывания с использованием алгебраического и геометрического языков. Использовать функционально-графические представления для решения и исследования тригонометрических уравнений, систем уравнений. Использовать готовые компьютерные программы для поиска пути решения и иллюстрации решения уравнений и неравенств Регулятивные: оценивать правильность выполнения действия на уровне адекватной ретроспективной оценки. Познавательные: владеть общим приемом решения задач. Коммуникативные: договариваться и приходить к общему решению в совместной деятельности, в том числе в ситуации столкновения интересов. ИНМ ЗИМ КЗУ ИНМ ЗИМ ИНМ ЗИМ ИНМ ЗИМ ИНМ ЗИМ ИНМ ЗИМ Вычислять значения тригонометрических функций, заданных формулами; составлять таблицы значений тригонометрических функций. Строить по точкам графики тригонометрических функций. Описывать свойства тригонометрических функций на основании их графического представления. Моделировать реальные зависимости с помощью формул и графиков. Интерпретировать графики реальных зависимостей. Использовать компьютерные программы для исследования положения на координатной плоскости графиков тригонометрических функций в зависимости от значений коэффициентов, входящих в формулу. Распознавать виды тригонометрических 5 Регулятивные: учитывать правило в планировании и контроле способа решения. Познавательные: осуществлять поиск необходимой информации для выполнения учебных заданий с использованием учебной литературы. Коммуникативные: учитывать разные мнения и стремиться к СП, ВП, УО Т, СР, РК КР СП, ВП, УО Т, СР, РК СП, ВП, УО Т, СР, РК СП, ВП, УО Т, СР, РК СП, ВП, УО Т, СР, РК КР СП, ВП, СП, ВП, УО Т, СР, РК СП, ВП, УО Т, СР, РК СП, ВП, УО Т, СР, РК Обратные тригонометрические функции* 2 3 1 Контрольная работа №9 1 1 1 Итоговое повторение XI класс Производная смысл и её геометрический Производная. 7 1 102 136 68 18 22 16 2 Производная степенной функции 2 Правила дифференцирования Производные функций 1 некоторых 2 элементарных Геометрический смысл производной 5 3 2 2 2 5 5 1 1 2 5 3 ИНМ ЗИМ функций. Строить более сложные графики на основе графиков тригонометрических функций; описывать их свойства. координации различных позиций в сотрудничестве КР КЗУ СЗУН ИНМ ЗИМ ИНМ ЗИМ ИНМ ЗИМ ИНМ ЗИМ СП, ВП, УО Т, СР, РК Формулировать определение производной функции. Использовать определение производной для нахождения производной простейших функций. Выводить формулы производных элементарных функций, сложной функции и обратной функции. Использовать правила дифференцирования функций. Находить мгновенную скорость движения точки. Использовать геометрический смысл производной для вывода уравнения касательной. Использовать полученные знания для описания и анализа реальных зависимостей Регулятивные: осуществлять итоговый и пошаговый контроль по результату. Познавательные: строить речевые высказывания в устной и письменной форме. Коммуникативные: учитывать разные мнения и стремиться к координации различных позиций в сотрудничестве. ИНМ ЗИМ СЗУН СЗУН Решение задач 3 5 3 Контрольная работа №1 Применение производной исследованию функций 1 1 1 к 14 20 10 Возрастание и убывание функции 2 2 1 Экстремумы функции 2 2 1 ИНМ ЗИМ СП, ВП, УО Т, СР, РК СП, ВП, УО Т, СР, РК СП, ВП, УО Т, СР, РК СП, ВП, УО Т, СР, РК СП, ВП, УО Т, СР, РК СП, ВП, УО Т, СР, РК КР КЗУ ИНМ ЗИМ СП, ВП, УО Т, СР, РК Находить интервалы монотонности функций. Находить точки экстремума функции. Доказывать теорему о достаточном условии экстремума. Находить наибольшее и наименьшее значение функций на интервале. 6 Регулятивные: учитывать правило в планировании и контроле способа решения. Познавательные: осуществлять поиск СП, ВП, УО Т, СР, РК СП, ВП, УО Применение производной к построению графиков функций Наибольшее функции и наименьшее Выпуклость перегиба* графика значения функции, точки 4 2 5 3 4 1 1 1 - Решение задач 2 6 2 Контрольная работа №2 1 1 1 Интеграл 13 16 9 Первообразная 1 Правила нахождения первообразных Площадь интеграл криволинейной трапеции 1 и Вычисление интегралов Вычисление интегралов площадей 2 1 с помощью 3 1 2 2 1 3 1 1 1 - 2 Применение производной и интеграла к решению практических задач* 2 3 1 Решение задач 2 3 2 ИНМ ЗИМ СЗУН ИНМ ЗИМ По графику производной определять интервалы монотонности, точки экстремума функции. Строить график, проводя полное исследование функции. Решать физические, геометрические, алгебраические задачи на оптимизацию. Моделировать реальные ситуации, исследовать построенные модели, интерпретировать полученный результат. ИНМ ЗИМ необходимой информации для выполнения учебных заданий с использованием учебной литературы. Коммуникативные: учитывать разные мнения и стремиться к координации различных позиций в сотрудничестве СЗУН КЗУ ИНМ ЗИМ ИНМ ЗИМ ИНМ ЗИМ ИНМ ЗИМ Т, СР, РК СП, ВП, УО Т, СР, РК СП, ВП, УО Т, СР, РК СП, ВП, УО Т, СР, РК КР Доказывать, что данная функция является первообразной для другой данной функции. Находить для функции первообразную, график которой проходит через точку, заданную координатами. Выводить правила отыскания первообразных. Выводить формулу Ньютона-Лейбница, вычислять площадь криволинейной трапеции. Решать задачи физической направленности. Моделировать реальные ситуации, исследовать построенные модели, интерпретировать полученный результат. ИНМ ЗИМ СЗУН ИНМ ЗИМ СЗУН 7 Регулятивные: различать способ и результат действия. Познавательные: владеть общим приемом решения задачи. Коммуникативные: договариваться и приходить к общему решению в совместной деятельности, в том числе в ситуации столкновения интересов. СП, ВП, УО Т, СР, РК СП, ВП, УО Т, СР, РК СП, ВП, УО Т, СР, РК СП, ВП, УО Т, СР, РК СП, ВП, УО Т, СР, РК СП, ВП, УО Т, СР, РК СП, ВП, УО Т, СР, РК Контрольная работа №3 Комбинаторика 1 7 Правило произведения. 1 Перестановки. 2 Размещения. 2 Сочетания и их свойства. 1 1 10 2 2 2 2 1 7 1 2 2 1 Бином Ньютона. 1 2 1 Элементы теория вероятностей. 7 12 7 События. Комбинаторика Противоположное событие. событий. Вероятность события. 1 Сложение вероятностей. Независимые вероятностей. события. 1 1 Умножение 2 2 2 2 3 1 1 1 2 Статическая вероятность. 1 2 1 Контрольная работа №4 1 1 1 КР КЗУ ИНМ ЗИМ ИНМ ЗИМ ИНМ ЗИМ Применять правило произведения для решения задач на нахождение числа объектов, вариантов или комбинаций. Применять свойства размещений, сочетаний, перестановок, разложения бинома Ньютона. Решать простейшие комбинаторные задачи, уравнения относительно n, содержащие выражения вида Pn, Amn , Cmn . ИНМ ЗИМ Регулятивные: осуществлять итоговый и пошаговый контроль по результату. Познавательные: строить речевые высказывания в устной и письменной форме. Коммуникативные: учитывать разные мнения и стремиться к координации различных позиций в сотрудничестве. ИНМ ЗИМ ИНМ ЗИМ ИНМ ЗИМ ИНМ ЗИМ ИНМ ЗИМ Решать задачи на нахождение вероятностей событий, в том числе с применением комбинаторики. Приводить примеры противоположных событий. Решать задачи на применение представление о геометрической вероятности. Вычислять вероятность суммы двух произвольных событий, двух несовместных событий. Решать задачи на вычисление вероятности произведения независимых событий. Представлять процессы и явления, имеющие вероятностный характер. Находить и оценивать вероятность наступления событий в простейших практических ситуациях. ИНМ ЗИМ Регулятивные: различать способ и результат действия. Познавательные: владеть общим приемом решения задачи. Коммуникативные: договариваться и приходить к общему решению в совместной деятельности, в том числе в ситуации столкновения интересов. СП, ВП, УО Т, СР, РК СП, ВП, УО Т, СР, РК СП, ВП, УО Т, СР, РК СП, ВП, УО Т, СР, РК СП, ВП, УО Т, СР, РК СП, ВП, УО Т, СР, РК СП, ВП, УО Т, СР, РК СП, ВП, УО Т, СР, РК СП, ВП, УО Т, СР, РК СП, ВП, УО Т, СР, РК КР КЗУ 8 Статистика Случайные величины. Центральные тенденции. 3 1 1 5 1 2 3 1 1 ИНМ ЗИМ ИНМ ЗИМ Вычислять частоту случайного события. Приводить примеры числовых данных, находить среднее, размах, моду, дисперсию числовых переборов. Находить и оценивать основные характеристики случайных величин. Исследовать случайные величины по их распределению ИНМ ЗИМ Меры разброса. 1 2 1 Итоговое повторение Итоговая контрольная работа 36 4 47 4 12 4 Регулятивные: учитывать правило в планировании и контроле способа решения. Познавательные: осуществлять поиск необходимой информации для выполнения учебных заданий с использованием учебной литературы. Коммуникативные: учитывать разные мнения и стремиться к координации различных позиций в сотрудничестве СП, ВП, УО Т, СР, РК СП, ВП, УО Т, СР, РК СП, ВП, УО Т, СР, РК КР КЗУ Принятые сокращения: ИНМ – изучение нового материала ЗИМ – закрепление изученного материала СЗУН – совершенствование знаний, умений, навыков УОСЗ – урок обобщения и систематизации знаний КЗУ – контроль знаний и умений Т – тест СП – самопроверка ВП – взаимопроверка СР – самостоятельная работа РК – работа по карточкам ФО – фронтальный опрос УО – устный опрос ПР – проверочная работа З – зачет * Количество часов на изучение каждой темы указано примерно, возможны изменения по решению предметного методического объединения образовательного учреждения **Тема: Тригонометрические функции - может быть перенесена в 11 класс по решению предметного методического объединения образовательного учреждения 9