Мармузевич

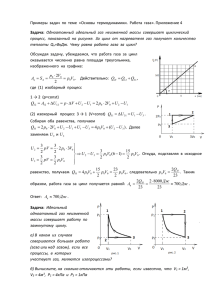
Урок №1
Тема: Теплота и работа. Работа в термодинамике.
Цели:
Образовательные:

Сформировать понятие работы в термодинамике (совершенная
газом и совершенная над газом)
Усвоить понятие теплопередачи

Сформировать понятие кругового (циклического) процесса
Развивающие:

Памяти, внимания

Культуры письменной и устной речи
Воспитательные:

Терпение

трудолюбие
Тип урока: урок усвоения новых знаний.
Методы обучения:
 репродуктивный
Формы организации урока: фронтальные
Оборудование и источники информации:
1.
Учебник по физике 11 кл Жилко, Лавриненко, Маркович
План урока:
1.
Организационный момент (2 мин.).
2.
Актуализация знаний (10 мин.).
3.
Формирование и применение новых способов действий (30 мин)
4.
Подведение итогов урока, задание на дом. (3 мин.)
1.Организационный момент
Вхожу в класс, здороваюсь, отмечаю отсутсвующих, проверяю
готовность к уроку.
2.Актуализация знаний.
Механическая работа А – скалярная физическая величина, равна
скалярному произведению вектора силы на вектор перемещения: A  F r
3.Формирование и применение новых способов действий.
3.1 Обмен энергии между термодинамической системой и
материальными объектами, окружающими ее (или между частями системы)
может происходить в двух эквивалентных формах: макроскопической, т.е.
путем выполнения работы, и микроскопической, т.е. путем теплообмена
(теплопередачи).
Работой в термодинамике называют процесс обмена энергией между
термодинамической системой и материальными объектами (телами и
полями), окружающими ее, который сопровождается изменением внешних
макропараметров состояния системы. Особый интерес представляет работа,
которую выполняет система при изменении ее объема под действием сил
давления.
3.2 Рассмотрим в качестве термодинамической системы идеальный газ,
который находится в цилиндре под подвижным поршнем. Пусть газ
квазистатически расширяется. При перемещении поршня на малое
расстояние dx сила давления газа F=pS
выполняет элементарную работу
dA=Fdx=pSdx=pdV.Где dV – изменение
объема газа. Если объем газа не
изменяется (изохорный процесс), то
работа газа равна 0.
Чтобы определить полную работу,
совершенную силой давления при
переходе газа из одного состояния в
другое, необходимо сложить
элементарные работы, т.е. вычислить
интеграл:
A   pdV . Это можно сделать только в том случае, если известно, как
изменяется давление газа при изменении его объема.
3.3 При изобарном процессе работа равна площади заштрихованного
прямоугольника.
p
0
V1
V2
V
В общем случае давление газа является функцией от его объема и
температуры, т.е. вид функции p=p(V) зависит от того, как изменяется
температура газа при переходе из начального состояния в конечное. По
этому работа газа определяется не только начальным и конечным состоянием
системы. Она зависит от вида процесса, в результате которого система
перешла из одного состояния в другое.
Т.о., работа является не функцией состояния термодинамической
системы, а функцией процесс перехода этой системы из одного состояния в
другое.
Если процесс не изобарный, то кривую p=p(V) можно представить как
ломаную, состоящую из большого количества изохор и изобар. Работа на
изохорных участках равна нулю, а суммарная работа на всех изобарных
n
участках будет A  lim
 pi Vi или A   p(V )dV , т.е. будет равна площади
V 0
i 1
заштрихованной фигуры. При изотермическом процессе (T=const) работа
равна площади заштрихованной фигуры:
p
V
Для определения полной работы нужно вычислить площадь
криволинейной трапеции под кривой процесса перехода системы из
начального состояния в конечное.
Если сила давления постоянная (p=const), то работа, которую
выполняет система, A=p(V2-V1). Если зависимость между силами давления и
объемом системы является линейной (p=αV+β), то работа, которую
выполняет система, A=<p>( V2-V1), где <p>=(p1+p2)/2.
3.4 Процесс, при котором термодинамическая система, прошедшая
некоторую последовательность состояний, снова возвращается в исходное
состояние, называют круговым или циклическим процессом. На p-V
диаграмме изображение квазистатического кругового процесса является
замкнутая кривая. Работа, которую выполняла система, равна площади,
ограниченной этой кривой.
p
2
1
V
Поскольку работа совершаемая системой при циклическом процессе,
не равна 0, то силы давления, которые ее выполняют, являются
неконсервативными. Как видно из рисунка, работа A1 при квазистатическом
расширении положительна, поскольку конечный объем V2 системы больше
ее начального объема V1(верхняя кривая). Работа А2 при квазистатическом
сжатии отрицательна, т.к. конечный объем V2 системы меньше ее начального
объема V1(нижняя кривая), причем A1>A2. Поэтому если кривая сжатия
расположена под кривой расширения, то полная работа, выполненная
системой за цикл, положительна (система отдает энергию внешним телам).
Если кривая сжатия расположена над кривой расширения, то работа, которую
выполняет система за цикл, отрицательна (система получает энергию от
внешних тел).
Т.о., работа в термодинамике является мерой макрофизического
процесса изменение внутренней энергии, обусловленного взаимодействием
термодинамической системы с внешними телами. Этот процесс всегда
сопровождается изменением макроскопических параметров системы под
действием приложенных к ней сил. Числовое значение работы определяется
не только начальным и конечным состояниями системы, но и видом
процесса. Поэтому работа в термодинамике является функцией процесса
смены состояния системы и зависит от того, в результате какого процесса
термодинамическая система перешла из одного состояния в другое.
3.5 Задача.
Некоторая масса идеального газа переходит из состояния В в состояние
С двумя различными способами: BaC и BbC, причем в процессе каждого
перехода газ совершает работу и происходит теплообмен. Одинакова ли при
каждом переходе работа, совершаемая газом?
Решение:
Работа А1, совершаемая газом в процессе BaC, равна площади фигуры
V1BaCV2. Работа A2, совершаемая газом в процессе BbC, равна площади
фигуры V1BbCV2. Из рисунка видно, что A1>A2.
p
B
a
b
C
V
V1
V2
4. Подведение итогов.
Что нового вы узнали?
Как определяется работа в термодинамике?
При каких условиях газ совершает работу?
Домашнее задание:
§23, упр.11 задачи 1, 5.