Вариант 1.
реклама
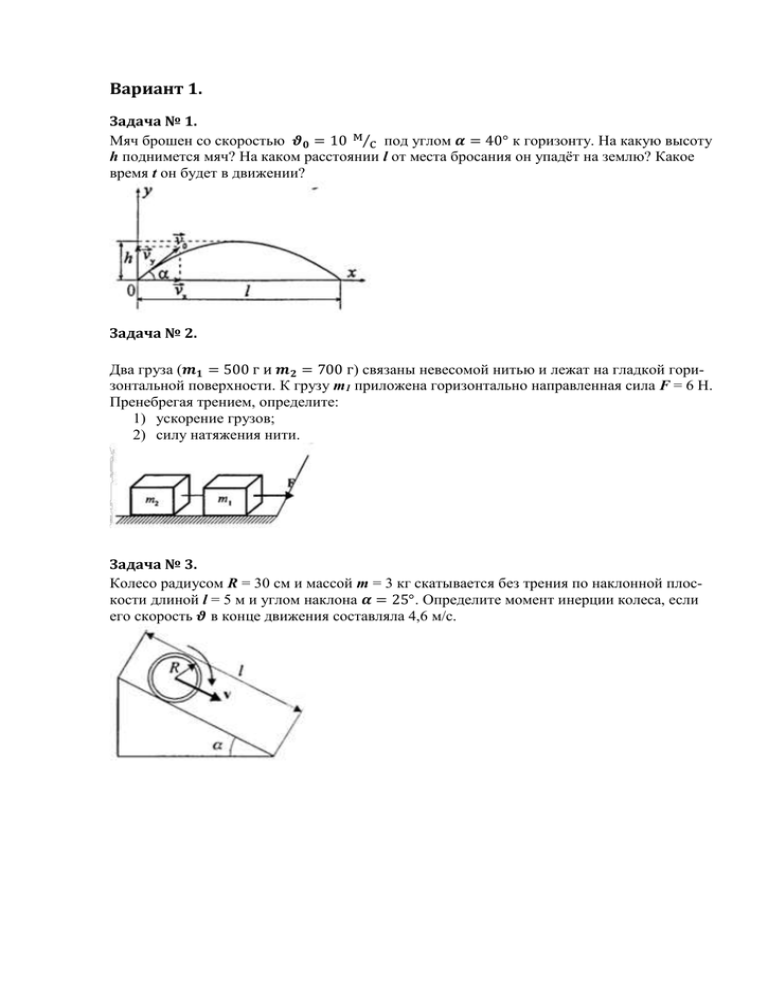
Вариант 1. Задача № 1. Мяч брошен со скоростью 𝝑𝟎 = 10 м⁄с под углом 𝜶 = 40° к горизонту. На какую высоту h поднимется мяч? На каком расстоянии l от места бросания он упадёт на землю? Какое время t он будет в движении? Задача № 2. Два груза (𝒎𝟏 = 500 г и 𝒎𝟐 = 700 г) связаны невесомой нитью и лежат на гладкой горизонтальной поверхности. К грузу m1 приложена горизонтально направленная сила F = 6 Н. Пренебрегая трением, определите: 1) ускорение грузов; 2) силу натяжения нити. Задача № 3. Колесо радиусом R = 30 см и массой m = 3 кг скатывается без трения по наклонной плоскости длиной l = 5 м и углом наклона 𝜶 = 25°. Определите момент инерции колеса, если его скорость 𝝑 в конце движения составляла 4,6 м/с. Вариант 2. Задача № 1. Тело 1 движется равноускоренно, имея начальную скорость 𝝑𝟏𝟎 = 2 м/с и ускорение a. Через время t = 10 с после начала движения тела 1 из этой же точки начинает двигаться равноускоренно тело 2, имея начальную скорость 𝝑𝟐𝟎 = 12 м/с и то же ускорение a. Найти ускорение a, при котором тело 2 сможет догнать тело 1. Задача № 2. В установке, изображённой на рисунке, угол 𝜶 наклонной плоскости с горизонтом равен 20°, массы тел m1 = 200 г и m2 = 150 г. Считая нить и блок невесомыми и пренебрегая силами трения, определите ускорение, с которым будут двигаться тела, если тело m2 опускается. Задача № 3. Через неподвижный блок в виде однородного сплошного циллиндра массой m = 0,2 кг перекинута невесомая нить, к концам которой прикреплены тела массами m1 = 350 г и m2 = 550 г. Пренебрегая трением в оси блока, опеределите: 1) ускорение груза; 𝑻 2) отношение 𝟐⁄𝑻 сил натяжения нити. 𝟏 Вариант 3. Задача № 1. Камень брошен горизонтально со скоростью 𝝑𝒙 = 15 м/с. Найти нормальное 𝒂𝒏 и тангенциальное 𝒂𝝉 ускорения камня через время t = 1 с после начала движения. Задача № 2. Тело массой m = 2 кг падает вертикально с ускорением a = 5 м/с2. Определите силу сопротивления при движении этого тела. Задача № 3. Человек массой m = 60 кг, стоящий на краю горизонтальной платформы массой M = 120 кг, вращающейся по инерции вокруг неподвижной вертикальной оси с частотой n1 = 10 мин-1 , переходит к её центру. Считая платформу круглым однородным диском, а человека – точечной массой, определите, с какой частотой n2 будет тогда вращаться платформа. Вариант 4. Задача № 1. С башни высотой h = 25 м горизонтально брошен камень со скоростью 𝝑𝒙 = 15 м/с. Какое время t камень будет в движении? На каком расстоянии l от основания башни он упадёт на землю? С какой скоростью 𝝑 он упадёт на землю? Задача № 2. В установке углы 𝜶 и 𝜷 наклонных плоскостей с горизонтом соответственно равны 30 и 45, массы тел m1 = 0,45 кг и m2 = 0,5 кг. Считая нить и блок невесомыми и пренебрегая силами трения, определите: 1) ускорение грузов; 2) силу натяжения нити. Задача № 3. Для демонстрации законов сохранения применяется маятник Максвелла, представляющий собой массивный диск радиусом R и массой m, туго насаженный на ось радиусом r, которая подвешивается на двух предварительно намотанных на неё нитях. Когда маятник опускают, то он совершает возвратно-поступательное движение в вертикальной плоскости при одновременном движении диска вокруг оси. Не учитывая силы сопротивления и момент инерции оси (масса оси мала), определите: 1) ускорение поступательного движения маятника; 2) силу натяжения нити. Вариант 5. Задача № 1. С башни высотой h0 = 25 м брошен камень со скоростью 𝝑𝟎 = 15 м/с под углом 𝜶 = 30 к горизонту. Какое время t камень будет в движении? На каком расстоянии l от основания башни он упадёт на землю? Задача № 2. Грузы одинаковой массы (m1 = m2 = 0,5 кг) соединены нитью и перекинуты через невесомый блок, укреплённый на конце стола. Коэффициент трения груза m2 о стол 𝝁 = 0,15. Пренебрегая трением в блоке, определите: 1) ускорение грузов; 2) силу натяжения нити. Задача № 3. Блок массой m = 1 кг укреплён на конце стола. Гири 1 и 2 одинаковой массы m1 = m2 = 1 кг соединены нитью, перекинутой через блок. Коэффициент трения гири 2 о стол 𝝁 = 0,1. Найти ускорение a, с которым движутся гири, и силы натяжения T1 и T2 нитей. Блок считать однородным диском. Трением в блоке пренебречь.







