динамика

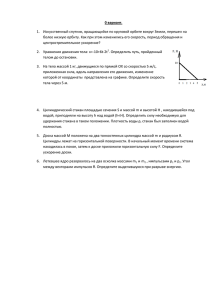
И. В. Яковлев
|
Материалы по физике
|
MathUs.ru
Движение со связями. Динамика
В некоторых задачах динамики наряду с законами Ньютона требуются дополнительные соотношения между ускорениями тел — так называемые уравнения кинематической связи.
Подвижный блок
[Овчинкин] → 2.6, 2.7, 2.8, 2.9.
Задача 1. (Всеросс., 2020, ШЭ, 10 ) Система состоит из двух массивных грузов, невесомых блоков и невесомой нерастяжимой верёвки.
Средний блок перемещают вниз с ускорением a0 = 5 м/с2 . Ускорение
свободного падения g = 10 м/с2 . Трение отсутствует.
1. Найдите ускорение груза массой m = 1 кг. Ответ укажите в м/с2 ,
округлив до целого числа.
2. Куда направлено ускорение тела массой 1 кг? 1 — вверх, 2 — вниз.
3. Чему равно натяжение нити? Ответ укажите в ньютонах, округлив до целого числа.
1) 10; 2) 1; 3) 20
Задача 2. (Савченко, 2.1.47 ) Найдите ускорение тел системы,
изображённой на рисунке. Сила F приложена по направлению
нити к одному из тел массы m. Участки нити по обе стороны от
лёгкого блока, прикреплённого к телу массы M , параллельны.
a1 =
F (M +4m)
;
2m(M +2m)
a2 =
FM
;
2m(M +2m)
a3 =
F
M +2m
Задача 3. («Физтех», 2018, 9 ) Система состоит из неподвижного блока Н, подвижного блока П и двух грузов 1 и 2 (см. рис.). Груз 1 движется с ускорением a1 = g/5, направленным вниз.
1) Найти ускорение груза 2.
2) Найти отношение масс грузов 1 и 2.
Массами нитей, блоков, а также трением в осях блоков можно пренебречь.
1) a2 =
g
;
10
2)
m1
m2
=
11
16
1
Задача 4. («Физтех», 2018, 9 ) Два подвешенных на нитях груза 1 и 2
различной массы могут двигаться в системе, состоящей из неподвижного блока Н и подвижного блока П (см. рис.).
1) Найти отношение масс грузов 1 и 2, если подвешенные грузы
остаются неподвижными.
2) Найти отношение масс грузов 1 и 2, если груз 1 движется с ускорением a1 = g/5, направленным вверх.
Массами нитей, блоков, а также трением в осях блоков можно пренебречь.
1)
m1
m2
=
1
;
2
m1
m2
2)
=
3
8
Задача 5. («Физтех», 2019, 9 ) В системе, показанной на рисунке, массы
грузов равны соответственно m1 = m3 = m = 0,1 кг, m2 = 3m. Первоначально систему удерживают, затем отпускают. Грузы приходят в движение. Начальные скорости всех грузов нулевые. Ускорение свободного
падения g = 10 м/с2 . Массы блоков и нитей по сравнению с массой грузов
пренебрежимо малы. Нерастяжимые нити свободно скользят по блокам.
1. Найдите скорость V1 груза 1 в тот момент, когда груз 2 опустится
на H = 0,5 м.
2. Найдите силу T2 натяжения нити, на которой подвешен груз 2.
1) V1 =
q
2
gH
5
=
√
2 ≈ 1,4 м/с; 2) T2 =
12
mg
5
= 2,4 Н
Задача 6. («Покори Воробьёвы горы!», 2014, 7–9 ) Из двух одинаковых цилиндрических роликов массы m, двух одинаковых грузов
массы m1 = 3m и лёгкой прочной нерастяжимой нити собрали механическую систему, показанную на рисунке. Один конец нити закреплен на «потолке», ролики не вращаются, нить скользит по роликам
без трения. Найти величину силы F , с которой нужно тянуть вверх
ось правого ролика, чтобы левый груз в этой системе двигался с постоянной по величине скоростью. Каким при этом будет ускорение
правого груза? Ускорение свободного падения считать известным.
F =
29
mg;
6
a=
1
g
3
(вниз)
Задача 7. (МОШ, 2012, 9 ) Изображённая на рисунке система состоит из грузов массами m и M , двух неподвижных и одного подвижного
блока. Не лежащие на блоках участки нитей вертикальны. Определите ускорения грузов, считая, что груз массой M при движении сохраняет горизонтальное положение, нити невесомы и нерастяжимы,
блоки лёгкие, трения нет.
Проекции на ось, направленную вниз: aM =
2
M −3m
g,
M +9m
am = −3aM
Задача 8. («Курчатов», 2014, 9 ) Три одинаковых груза массой m соединены c помощью идеальных нитей и двух идеальных блоков, как показано на
рисунке. Найдите величину и направление ускорения нижнего груза.
a=
2g
,
3
направлено вниз
Задача 9. («Покори Воробьёвы горы!», 2019, 7–9 ) На легкой нерастяжимой веревке с помощью трех блоков подвешены два груза. Блоки легкие, вращаются без трения, веревка по ним не скользит. Один
из концов веревки закреплен на шкиве выключенной лебедки. Удерживая груз 2 на месте, включают лебедку и сразу после этого груз
2 отпускают. Лебедка вытягивает веревку с постоянной скоростью
u = 2 м/с. Спустя какое время скорости грузов окажутся равны по
модулю? Соотношение масс грузов m2 : m1 = 2. Ускорение свободного
падения g ≈ 10 м/с2 .
≈ 0,3 с
3u
2g
t=
= 2,5 с
5h
2u
t=
Задача 10. («Покори Воробьёвы горы!», 2019, 7–9 ) Система из двух
легких прочных тросов, двух неподвижных и двух подвижных блоков и двух грузов подвешена к потолку (см. рисунок). Все блоки —
легкие и вращаются без трения, тросы по блокам не скользят. Конец
одного из тросов закреплен на шкиве выключенной лебедки, груз 2
удерживают на месте. Этот груз аккуратно отпускают, а затем почти
сразу включают лебедку, которая начинает вытягивать трос с постоянной скоростью u = 1,5 м/с. За какое время груз 2 поднимется на
высоту h = 1,5 м? Отношение масс грузов m1 : m2 = 4. Временем
разгона грузов и их смещением при разгоне пренебречь.
Задача 11. («Росатом», 2011, 9 ) На гладкой горизонтальной
поверхности находятся два тела с массами m и m/2. К телам
прикреплены невесомые блоки, и они связаны невесомой и нерастяжимой нитью так, как показано на рисунке. К концу нити прикладывают постоянную силу F . Найти ускорение конца нити.
a=
17F
m
3
Задача 12. («Росатом», 2020, 10 ) Через блоки переброшена
легкая нерастяжимая веревка, к одному концу которой прикреплено тело массой m, второй конец которой прикреплен к горизонтальному потолку. Левый блок имеет массу 2m, правый —
m, причем масса блоков практически сосредоточена в их осях.
Систему удерживают, а в некоторый момент времени веревку 1
перерезают и предоставляют систему самой себе. Найти ускорения тел после этого.
a1 =
4
g;
5
a2 =
6
g
5
Задача 13. («Росатом», 2020, 10 ) Имеется система трех грузов и двух
блоков, показанная на рисунке. Блоки и нити в системе невесомы, нити
нерастяжимы. Массы двух нижних тел равны m и 4m. При какой массе
третьего тела M одно из тел может находиться в покое?
M =
16
m
5
Задача 14. («Росатом», 2020, 11 ) Механическую систему, состоящую из двух невесомых подвижных блоков, двух тел массой m и
2m и невесомых и нерастяжимых нитей, удерживают в определенном положении (см. рисунок). В некоторый момент времени систему
отпускают. Найти ускорения тел.
a1 =
1
g;
3
a2 =
4
g
3
Задача 15. («Росатом», 2020, 11 ) Имеется система из трех тел с
массами m, 2m и 3m и двух невесомых блоков,один из которых неподвижный, второй — подвижный. Тела m и 3m привязывают m к веревке, которую пропускают через блоки, тело 2m привязывают к оси
подвижного блока. До некоторого момента тела удерживают, а затем
отпускают. Найти ускорения тел.
a1 =
8
g;
5
a2 =
2
g;
5
a3 =
4
g
5
4
Задача 16. («Росатом», 2020, 9–10 ) На шероховатой горизонтальной поверхности покоятся два бруска с одинаковой
массой m. Коэффициенты трения брусков о поверхность равны µ и 2µ. К брускам привязана верёвка, которая переброшена
через лёгкий горизонтально расположенный блок (см. рисунок; вид сверху). Какое минимальное горизантольное ускорение ~a нужно сообщить блоку, чтобы оба бруска стронулись с
места?
a>
µg
2
Задача 17. (Всеросс., 2018, МЭ, 10 ) Найдите модуль и направление ускорения, с которым нужно двигать конец нити для того, чтобы правый груз,
имеющий массу m = 3 кг, оставался неподвижным. Массой нити и блоков можно пренебречь. Нить нерастяжима, трение отсутствует. Ускорение
свободного падения принять равным g = 10 м/с2 .
a = g/4 (вниз)
Задача 18. (МОШ, 2017, 9 ) Найдите ускорение груза массой 3m
в системе, изображённой на рисунке. Нить невесома и нерастяжима, блоки невесомы, трение отсутствует. Чему равна реакция со
стороны нити, действующая на неподвижный верхний блок?
a=
g
;
8
R=
√
3 2
mg
8
Задача 19. (МОШ, 2007, 9 ) Найдите ускорение груза
1 в системе, изображённой на рисунке. Массы грузов 1
и 2 равны M , массы грузов 3 и 4 равны m. Грузы 3 и
4 касаются грузов 1 и 2, участки нити, не лежащие на
блоках, горизонтальны или вертикальны. Нить невесома
и нерастяжима, блоки лёгкие, трения нет.
A=
mg
M +2m
Задача 20. (МОШ, 2007, 10 ) Найдите ускорения грузов 1
и 2 и силу натяжения нити в системе, изображенной на рисунке. Массы грузов 1, 2, 3 и 4 равны соответственно M1 ,
M2 , m1 и m2 . Грузы 3 и 4 касаются грузов 1 и 2, участки
нити, не лежащие на блоках, горизонтальны или вертикальны. Нить натянута, невесома и нерастяжима, блоки лёгкие,
трение отсутствует.
1
M1 +m1
2g
1
+ M +m
+ m1 + m1
2
2
1
2
; a1 =
T
M1 +m1
(вправо), a2 =
T
M2 +m2
a=
13
g
74
5
T =
(влево)
Задача 21. («Росатом», 2015, 10 ) На гладком горизонтальном
столе находятся два тела с массами M и 3M . Одинаковые грузы
с массой m (m = M/4) связаны невесомой нитью, переброшенной
через блоки. Тела отпускают. Найти ускорение тела M .
Задача 22. (МОШ, 2006, 10 ) В системе, изображённой на рисунке, массы всех трёх грузов одинаковы и равны m. Нить, соединяющая грузы 1 и 2, невесома и нерастяжима; её участки, не
лежащие на блоках, вертикальны или горизонтальны; блоки невесомы, трения нет. Груз 3 движется по горизонтальной плоскости,
не опрокидываясь. Найдите ускорения всех трёх грузов. Ускорение свободного падения равно g.
a1 =
g
5
(вниз); a2 =
g
√
5
(влево вниз, ϕ = arctg 21 ); a3 =
2g
5
(влево)
Задача 23. (МОШ, 2006, 11 ) В системе, изображённой на рисунке, цилиндрический груз массой m1 движется внутри цилиндрического канала чуть большего диаметра, просверленного внутри
тела массой m2 . Нить, соединяющая грузы m1 и m3 , невесома и
нерастяжима, блоки невесомы, трения нет. Чему равно ускорение
груза массой m1 ? Ускорение свободного падения равно g, участок
нити между блоками горизонтален.
a1 = g
q
2
(2m1 m3 )2 +(m2 m3 −m1 m2 −m1
)
(m1 +m2 )(m1 +m3 )+m1 m3
2
, ϕ = arctg
2
m2 m3 −m1 m2 −m1
2m1 m3
Задача 24. (МОШ, 2009, 9 ) В системе, показанной на рисунке, неподвижный блок прикреплён к потолку комнаты, а все грузы удерживают неподвижными так, чтобы отрезки лёгкой нерастяжимой нити, не лежащие на
блоках, были вертикальны. Грузы массами m2 и m3 подвешены к осям
блоков на жёстких лёгких стержнях. Все блоки лёгкие и могут вращаться
вокруг своих осей без трения. Определите ускорение груза массой m2 после одновременного отпускания всех грузов. Ускорение свободного падения
равно g.
a2 =
4m1 m2 +3m1 m3 +m2 m3
g
4m1 m2 +m1 m3 +m2 m3
(a2 > g)
Задача 25. («Росатом», 2019, 11 ) Имеется 2019 неподвижных и 2018 подвижных блоков,
через которые переброшена невесомая, нерастяжимая веревка (см. рисунок). К осям подвижных
блоков прикреплены 2018 тел массой m, к концам веревки — тела массой m и m/2.
Найти величину и направление ускорения самого левого тела.
a1 =
4037
g
8075
≈
1
g
2
6
Задача 26. (Всеросс., 1998, ОЭ, 9 ) Система грузов (см. рисунок)
с массами m1 = m3 = 10 кг и m2 = 20 кг сначала находится в покое, трение отсутствует, а массы блоков и нитей пренебрежимо малы.
Затем к грузу m1 прикрепили довесок ∆m1 = 1,25 кг, к грузу m3 —
довесок ∆m3 = 5 кг, и систему предоставили себе самой. В каком
направлении и с какими ускорениями станут двигаться грузы?
Проекции на ось, направленную вертикально вниз: a1 = 0, a2 = − g8 , a3 =
g
4
Задача 27. (МОШ, 2016, 9 ) В системе, изображённой на рисунке, определите ускорения груза и двух одинаковых блоков 1 и 2. Нить невесома и
нерастяжима, массы блоков пренебрежимо малы по сравнению с массой груза M , трения нет. Ускорение свободного падения g известно.
a = g, a1 = 2g, a2 = 0
Задача 28. (МОШ, 2016, 11 ) Найдите величины и направления ускорений
осей всех блоков, изображённых на рисунке. Массы бруска и верхнего блока равны соответственно M и m. Остальные блоки невесомы, нить также
невесома и нерастяжима. Трение в осях блоков пренебрежимо мало. Нити
по блокам не проскальзывают, не лежащие на блоках участки нитей вертикальны. В начальный момент система покоилась.
a1 = a2 = a3 = 0, a4 = −2g, a5 = g
Задача 29. (МОШ, 2016, 9 ) Невесомая нерастяжимая нить перекинута
через идеальный блок. К одному концу нити прикреплён груз массой m2 ,
а другой конец нити наматывается на невесомую катушку радиусом r,
расположенную внутри ящика массой m1 . Катушка вращается электродвигателем с постоянной угловой скоростью ω. Участки нити, не прилегающие к блоку и катушке, в процессе движения вертикальны, система
крепления катушки к ящику и электродвигатель очень лёгкие. Найдите
модуль ускорения a груза m2 .
a=
m2 −m1
m2 +m1
g
7
Задача 30. (МОШ, 2018, 9 ) На гладком горизонтальном столе находится механическая система, изображёная на рисунке.
Массы тел 4 кг и 1 кг. Свободный конец нити тянут в горизонтальном направлении с ускорением 14 м/c2 (см. рисунок).
Найдите силу натяжения нити. Блок невесом, нить невесома
и нерастяжима, трения в оси блока нет, ускорение свободного
падения равно 10 м/c2 .
F =
1 +
1
m
m+M
a+g
= 20 Н
Задача 31. («Физтех», 2018, 11 ) Систему из трёх брусков, находящихся на горизонтальном столе, приводят
в движение, прикладывая горизонтальную силу F (см.
рис.). Коэффициент трения между столом и брусками и
между соприкасающимися брусками m1 и m2 равен µ.
Массы брусков m1 = m, m2 = 2m, m3 = 3m. Массой горизонтально натянутой нити, массой
блока и трением в его оси пренебречь.
1) Найти силу натяжения нити, если бруски m1 и m2 скрепить, а параметры F , m, µ подобрать такими, чтобы бруски двигались по столу как одно целое.
2) Найти силу натяжения нити, если параметры F , m, µ подобраны так, что нескреплённые
бруски m1 и m2 движутся друг по другу, а бруски m1 и m3 — по столу.
1) T0 =
F
4
; 2) T =
6
(F
17
− 2µmg)
Задача 32. (Всеросс., 2014, РЭ, 10 ) К двум лёгким подвижным блокам подвешены грузы, массы которых равны m1 и m2 . Лёгкая нерастяжимая нить, на которой висит блок с грузом m1 , образует с горизонтом угол α. Грузы
удерживают в равновесии (см. рисунок). Найдите ускорение
грузов сразу после того, как их освободят. Считайте, что радиусы блоков r L.
1
2
m1 −m2 sin α
a1 = g m
, a2 = −a1 sin α (ось вниз)
+m sin2 α
Задача 33. (Всеросс., 2011, РЭ, 11 ) На гладкой горизонтальной поверхности покоится уголок массы M , который с помощью лёгкой нити
и двух блоков соединён со стенкой и бруском массы m (см. рисунок).
Брусок касается внутренней поверхности уголка. Нити, перекинутые
через блок, прикреплённый к стене, натянуты горизонтально.
Вначале систему удерживают в состоянии покоя, а затем отпускают. Найдите ускорение a уголка.
Блоки лёгкие. Трение в системе отсутствует.
a=
2mg
M +5m
8
Задача 34. («Покори Воробьёвы горы!», 2015, 10–11 ) Один
из концов лёгкой нерастяжимой нити прикреплен к раме
массой M , а на другом подвешен груз массы m. С помощью системы идеальных блоков и этой нити груз и рама
связаны с неподвижной стенкой. Если раму удерживать, то
неподвижный груз касается рамы. Трения между грузом и
рамой нет, коэффициент трения между рамой и горизонтальной поверхностью равен µ. Найти ускорение рамы после
отпускания. Ускорение свободного падения g.
если µ >
0,
если µ 6
(4−µ)m−µM
g,
M +(17−4µ)m
28g
19
и
7g
19
10
g
13
и
5
g
13
Задача 37. («Росатом», 2017, 11 ) В системе двух тел с массами m
и 2m, связанных нерастяжимой и невесомой нитью, второй конец которой
прикреплён к потолку, и двух невесомых блоков (см. рисунок), ускорения
блоков известны и равны a и 2a. Какими силами нужно действовать на
блоки?
F1 = 24ma + 4mg, F2 = 28ma + 2mg
9
(
4m
;
M +m
4m
M +m
Задача 36. («Росатом», 2017, 11 ) Блок склеен из двух дисков с радиусами R и 2R, насаженных на одну и ту же горизонтальную ось, и подвешен
к горизонтальному потолку. На блоки намотана невесомая нерастяжимая
нить, к которой прикреплён груз массой m, как это показано на рисунке.
Нить охватывает также нижний блок, размеры которого подобраны так,
что все отрезки нити вертикальны. Второй груз массой 3m прикреплён
к оси нижнего блока. Найти ускорения тел. Блоки невесомы.
A=
Задача 35. («Росатом», 2017, 10 ) Блок склеен из двух дисков с радиусами R и 2R, насаженных на одну и ту же горизонтальную ось, и подвешен
к горизонтальному потолку. На блоки намотана невесомая нерастяжимая
нить, к которой прикреплён груз массой m, как это показано на рисунке.
Нить охватывает также нижний блок, размеры которого подобраны так,
что все отрезки нити вертикальны. Второй груз массой 3m прикреплён
к оси нижнего блока. Найти ускорения тел. Блоки невесомы.
Задача 38. (МОШ, 2018, 10 ) С каким и в какую сторону направленным ускорением нужно
двигать средний блок, чтобы левый груз, имеющий массу 2 кг, оставался неподвижным? Массой
нити и блоков можно пренебречь. Нить нерастяжима, трение отсутствует. g = 10 м/с2 .
Вниз с ускорением g/2
Задача 39. (МОШ, 2017, 10 ) Если приложить силу F к телу массой m (рис. 1), то оно начнёт
двигаться с ускорением a1 = 0,20 м/с2 . С каким ускорением a2 придёт в движение это же тело,
если силу F приложить к телу массой 3m (рис. 2)? Тела находятся на гладкой горизонтальной
поверхности. Массой блока и нерастяжимых нитей можно пренебречь.
a2 = 2a1 = 0,40 м/с2
Задача 40. (МОШ, 2015, 10 ) Система, показанная на рисунке, состоит из трёх блоков, трёх одинаковых грузов, двух нитей (первая
нить показана на рисунке сплошной линией, вторая — пунктирной) и
короткой верёвочки. К концу первой нити, перекинутой через средний и левый блоки, прикреплён первый груз массой m. К концу второй нити, перекинутой через правый и средний блоки, прикреплён
второй груз массой m. Третий груз такой же массой подвешен на верёвочке к оси правого блока. Участки нитей, не лежащие на блоках,
вертикальны. Все блоки и нити можно считать невесомыми, нити и
верёвочку нерастяжимыми, а силы трения пренебрежимо малыми.
При вращении среднего блока первая и вторая нити не мешают друг
другу. Найдите модули ускорений грузов.
Модули ускорений грузов одинаковы и равны a = g/3
10
Задача 41. (МОШ, 2011, 10–11 ) В системе, изображённой на рисунке,
все блоки — невесомые и вращаются без трения, все нити — невесомые
и нерастяжимые (их жёсткость велика по сравнению с жёсткостью пружины). Пружина также невесома. Система находится в покое. При какой
массе груза M груз 1 сразу после пережигания нити в точке A будет иметь
ускорение большее, чем g?
M > 6m
Задача 42. (Всеросс., 2012, финал, 10 ) На платформе
с прямоугольным выступом высотой h лежит небольшое
тело массой m. К нему прикреплён один конец невесомой нерастяжимой нити, перекинутой через идеальный
блок, установленный на выступе платформы (рис.). Второй конец нити закреплён на вертикальной стене так,
что участок нити между блоком и стеной горизонтален.
Платформу перемещают от стены с постоянной скоростью v. С какой силой F нужно тянуть платформу в тот момент, когда участок нити над
платформой составляет угол α с горизонтом? Сила F горизонтальна и лежит в плоскости рисунка. Коэффициент трения между телом и платформой µ, между платформой и полом трения
нет. Считайте, что во время движения груз от платформы, а платформа от пола не отрываются.
F =
ma(1−cos α−µ sin α)+µmg
,
cos α+µ sin α
где a =
v2
h
tg3 α
Подвижный клин
Задача 43. (МОШ, 2017, 9 ) На горизонтальной плоскости находится клин массой M , наклонная поверхность которого образует угол α с горизонтом. На клине лежит маленький шарик массой m, который соединён невесомой нерастяжимой нитью длиной L с неподвижной осью O, расположенной вне клина. Клин
удерживают в таком положении, что нить параллельна наклонной поверхности клина. Трение в системе отсутствует. Клин отпускают, предоставляя системе возможность двигаться. Найдите
модули ускорений шарика и клина относительно горизонтальной плоскости в момент сразу
после отпускания клина. Нить можно считать очень длинной.
a=
mg sin2 α cos α
,
M +m sin2 α
A=
mg sin α cos α
M +m sin2 α
11
Задача 44. («Физтех», 2019, 11 ) На гладкой горизонтальной поверхности стола покоится клин. Гладкая наклонная поверхность
клина образует с горизонтом угол α такой, что cos α = 0,6. Если шайбе, находящейся у основания клина, сообщить начальную
скорость V0 вдоль поверхности клина (см. рис.), то к моменту
достижения шайбой высшей точки траектории скорость шайбы
уменьшается в n = 5 раз. В процессе движения шайба безотрывно скользит по клину, а клин по столу. Ускорение свободного падения g. Известными считать
V0 , n и α.
1. Найдите отношение m/M массы шайбы к массе клина.
2. На какую максимальную высоту H, отсчитанную от точки старта, поднимается шайба
в процессе движения по клину?
3. Через какое время T после старта шайба поднимается на максимальную высоту?
1)
m
M
=
1
;
2
2) H =
2
11 V0
;
25 g
3) T =
11 V0
10 g
Задача 45. Клин массой M находится на гладкой горизонтальной поверхности. По наклонной
поверхности клина, образующей угол α с горизонтом, соскальзывает без трения брусок массой m. Найти ускорение клина.
sin α cos α
A = gm
M +m sin2 α
Задача 46. (Савченко, 2.1.50 ) На гладкой горизонтальной плоскости находится клин с углом α при основании. Тело массы m,
положенное на клин, опускается с ускорением, направленным под
углом β > α к горизонтали. Определите массу клина.
tg α
M = m tg β−tg
α
Задача 47. (Савченко, 2.1.49 ) К свободному концу нити, прикрепленной к стенке и переброшенной через ролик, подвешен
груз. Ролик закреплен на бруске массы m0 , который может скользить по горизонтальной плоскости без трения. В начальный момент нить с грузом отклоняют от вертикали на угол α и затем
отпускают. Определите ускорение бруска, если угол, образованный нитью с вертикалью, не меняется при движении системы.
Чему равна масса груза?
sin α
a = g tg α; m = m0 (1−sin
α)2
Задача 48. (МОШ, 2017, 10 ) Какое расстояние S пройдёт нижняя призма, когда верхняя коснётся плоскости? Размеры и массы
тел указаны на рисунке. В начальный момент система покоилась.
Трения нет. Чему равен угол β между направлением вектора абсолютной скорости верхней призмы и горизонталью, если наклонная поверхность нижней призмы образует с горизонтом угол α?
S=
m(d−b)
;
M +m
β = arctg
M +m
M
12
tg α
Задача 49. (Всеросс., 1999, финал, 9 ) На гладком горизонтальном столе стоит клин массой M с углом наклона α при основании
(см. рисунок). На поверхности клина находится брусок массой m,
привязанный лёгкой нитью к стене. Нить перекинута через невесомый блок, укреплённый на вершине клина. Отрезок нити AB
параллелен горизонтальной поверхности стола. Вначале систему
удерживают, а затем отпускают. При этом брусок начинает скользить по наклонной поверхности клина. Силы трения отсутствуют.
1) Найдите ускорение клина в этом случае.
2) Полагая α заданным, найдите, при каком отношении масс клина и бруска такое скольжение возможно.
m sin α
; 2)
1) a = g M +2m(1−cos
α)
M
m
>
(1−cos α)2
cos α
Задача 50. (МОШ, 2012, 10 ) На гладкой горизонтальной
поверхности находится клин с высотой h = 30 см и шириной
основания d = 40 см. На его гладкой наклонной плоскости находится маленькая шайба, соединённая с клином при помощи
невесомой нерастяжимой нити, перекинутой через два блока (см. рисунок). Блоки невесомые и вращаются без трения,
масса клина в n = 8 раз больше массы шайбы. С каким ускорением начнёт двигаться клин после отпускания? Ускорение
свободного падения считайте равным g ≈ 9,8 м/с2 . Движение
клина — поступательное.
2 sin α
A = g n+5−4
=
cos α
6
g
49
≈ 1,2 м/с2
Разные системы
Задача 51. («Росатом», 2016, 9 ) Тело в форме куба массой 10m удерживают на гладкой горизонтальной поверхности. Второе тело массой m
подвешено к потолку на невесомой нити, составляющей угол α с вертикалью, и касается куба. Тела отпускают. Найти ускорения тел. Трением
пренебречь. Считать, что куб не переворачивается.
a=
g sin α
,
1+10 cos2 α
A=
g sin α cos α
1+10 cos2 α
Задача 52. (Всеросс., 2008, ОЭ, 9 ) Массивный шарик насажен на стержень, жёстко закреплённый под углом α к горизонту, и может без трения
скользить по нему. К шарику на лёгкой нерастяжимой нити подвешен точно такой же шарик. Другая нить удерживает верхний шарик на стержне
в равновесии (рис.).
1) С какими ускорениями начнут движение шарики сразу после пережигания верхней нити?
2) Пусть теперь шарики соединены не нитью, а лёгкой пружиной. С какими ускорениями шарики начнут движение в этом случае?
1) a =
2g sin α
,
1+sin2 α
b=
2g sin2 α
;
1+sin2 α
2) a = 2g sin α, b = 0
13
Задача 53. («Росатом», 2019, 10 ) Три одинаковых массивных шарика
связывают двумя невесомыми стержнями и удерживают в вертикальной
плоскости так, что шарики касаются внутренней поверхности закрепленной сферы (см. рисунок). В некоторый момент шарики отпускают. Найти
ускорения шариков сразу после их освобождения. Трением пренебречь.
a=
√
2+ 2
g
6
Задача 54. («Росатом», 2020, 11 ) Нерастяжимая нить
прикреплена к маленькой массивной бусинке в точке A,
затем переброшена через блоки B и C, затем пропущена через сквозной отверстие D в той же бусинке, а затем прикреплена к потолку в точке E. Первоначально бусинку удерживают так, что участок нити AB вертикален,
∠F DE = α (отмечен на рисунке одной дугой), ∠F DC = 3α (отмечен на рисунке двумя дугами).
Затем бусинку отпускают. Найти ускорение бусинки сразу после этого. Трения между нитью и
стенками отверстия в бусинке отсутствует.
α+cos 3α
a = g √3+2 sincos
α+2 sin 3α+2 cos 2α
Задача 55. (МОШ, 2011, 10 ) На горизонтальном столе
находятся два одинаковых грузика, связанные невесомой
и нерастяжимой нитью, образующей равнобедренный треугольник AOB (см. рисунок). Углы при основаниях треугольника равны α. В точке O к этой нити привязана другая нить, которую удерживают вертикально слегка натянутой. С каким минимальным ускорением нужно начать
поднимать точку O, чтобы грузы оторвались от стола в
момент начала своего движения?
amin = g ctg2 α
Задача 56. (МОШ, 2019, 11 ) Бруски равных масс m = 1 кг связаны нитью длины 2L = 50 см
и стоят на горизонтальном полу, коэффициент трения которого с брусками µ = 0,2. Нить за её
середину начинают тянуть с постоянной вертикальной силой F = 10 Н. Ускорение свободного
падения g = 10 м/с2 .
1. Каковы скорости брусков при столкновении? Выразите ответ в м/с и округлите до десятых.
2. При каком максимальном значении силы F бруски не столкнутся? Выразите ответ в Н и
округлите до десятых.
1) 1,4 м/с; 2) 3,3 Н
14
Задача 57. (МОШ, 2018, 11 ) На подставку в форме прямой четырёхугольной призмы (в основании ромб ABCD,
∠ABC = α, боковые грани — прямоугольники) кладут два
маленьких груза, связанных тонкой невесомой натянутой
нитью, и отпускают их. Трения нет. Массы грузов одинаковы. Середина нити (точка P ) движется по диагонали DB.
Грузы движутся по прямым линиям симметрично относительно плоскости BB 0 D0 D. Найдите модули ускорений грузов и модуль ускорения середины нити. Ускорение свободного падения g = 10 м/с2 .
a = A = g sin
α
2
Задача 58. (Всеросс., 2019, финал, 10 ) На гладком горизонтальном столе лежит гантель, состоящая из двух маленьких по размеру шайб, имеющих массы m1 и m2 , соединенных легким жестким (деформации стержня
малы по сравнению с его размерами) стержнем длины L. В момент времени t = 0 на шайбу с массой m1 начинает действовать постоянная по
величине горизонтальная сила F . Направление действия силы всегда составляет один и тот же острый угол α со стержнем (рис.). Считайте известным, что при таком
движении угловое ускорение стержня является постоянным.
В некоторый момент времени τ после начала действия силы стержень на мгновение оказался
не напряженным (то есть ни сжатым, ни растянутым).
1. Найдите угловую скорость ω вращения стержня в момент времени τ .
2. Найдите угловое ускорение стержня dω/dt.
3. Чему равен промежуток времени τ ?
4. Найдите угол поворота стержня к моменту времени τ .
ω=
q
F cos α dω
; dt
m1 L
=
F sin α
;
m1 L
τ =
q
m1 L cos α
;
F sin2 α
ϕ=
1
2
ctg α
15