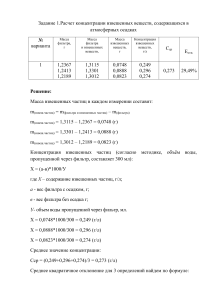
Само решение необходимо переделать под

ЗАДАЧА
Само решение необходимо переделать под нужный вариант:
при n=8, λ=4, tобс=1
Необходимо оценить работу автоматической телефонной станции
(АТС), которая имеет n=8 линий связи. Моменты поступления вызовов на
станцию являются случайными и независимыми друг от друга. Средняя
плотность потока равна λ=1 вызову в единицу времени. Продолжительность
каждого
разговора
является
величиной
случайной
и
подчинена
показательному закону распределения. Среднее время одного разговора
равно tобс = 2 единицы времени.
Автоматические телефонные станции относятся к типу систем
обслуживания с потерями (с отказами). Абонент получает отказ в случае,
если все линии заняты.
Для определения основных показателей работы АТС необходимо
рассчитать значение поступающей нагрузки в Эрлангах Ψ и вероятности, что
из n-линий k будет занято
Для расчета используются формулы:
Далее следует определить вероятность отказа Ротказа , среднее число
занятых и среднее число свободных линий, коэффициенты занятости и
простоя линий и сделать вывод о качестве обслуживания абонентов и
эффективности использования линий связи.
1. Определим значение поступающей нагрузки Ψ по формуле
    t обс = 1·2=2
2. Найдем вероятность того, что все линии связи свободны по формуле:
P0 
1
,
n
k

k  0 k!
где n количество линий связи, к=1,2,…,n
P0 
1

2
2
2
2
28
 

 ... 
0! 1 1  2 1  2  3
1 2  3  4  5  6  7  8
1
1

 0,135
1  2  2  1,33  0,67  0,27  0,09  0,025  0,0063 7,39
0
1
2
3
Вероятность того, что все линии связи будут свободны, составляет
13,5%
3. Рассчитаем вероятности занятости k-линий из n, по формуле
Pk 
k
k!
 P0
k=1, P1 
21
 0,135  0,27
1
k=2, P2 
22
 0,135  0,27
1 2
k=3, P3 
23
 0,135 =0,18
1 2  3
k=4, P4 
24
 0,135  0,09
1 2  3  4
25
 0,135  0,036
k=5, P5 
1  2  ...  5
26
 0,135  0,012
k=6, P6 
1  2  ...  6
27
k=7, P7 
 0,135  0,0034
1  2  ...  7
k=8, P8 
28
 0,135  0,00085
1  2  ...  8
4. Найдем вероятность того, что все линии связи заняты, т.е.
вероятность отказа, по формуле:
Pотказ
Pотказ
n
n
k


n! k 0 k!
28
  6,39  0,63  7,39  0,085
8!
Вероятность отказа равна 8,5%.
5. Найдем среднее число занятых линий по формуле:
 k P0

k 1 k  1!
n
n зан
24
28
 21 2 2 23

nзан    

 ... 
  0,135  1,99
1
1
1

2
1

2

3
1

2

3

4

5

6

7


Среднее число занятых линий равняется 1,99.
6. Коэффициент занятости линий
nзан 1,99
=
 0,25
n
8
7. Найдем среднее число свободных линий по формуле:
nсвоб   n  k Pk
n
k 0
nсвоб  8  0,135  7  0,27  6  0,27  5  0,18  4  0,09 
 3  0,036  2  0,012  1  0,0034  5,99
Среднее число свободных линий равно 5,99
8.Коэффициент простоя линий
nсвоб 5,99

 0,75
n
8
Коэффициент простоя можно было посчитать другим методом 10,25=0,75
k
k!
Pk
k  1P
0
1
0,135
1,08
1
2
0,27
1,89
0,27
2
2
0,27
1,62
0,54
3
1,33
0,18
0,9
0,54
4
0,67
0,09
0,36
0,36
5
0,27
0,036
0,108
0,18
6
0,09
0,012
0,024
0,072
7
0,025
0,0034
0,0034
0,024
8
0,0063
0,00085
0
0,0069
Итого
7,39
1
5,99
1,99
k
Вывод:
качество
k
 k  P0
k  1!
обслуживания
абонентов
неплохое
так
как
вероятность отказа составляет 8,5%, но эффективность использования линий
низкая потому что очень высокий процент простоя линий связи 75%.