Муниципальное бюджетное общеобразовательное учреждение «Побединская средняя общеобразовательная школа»
реклама

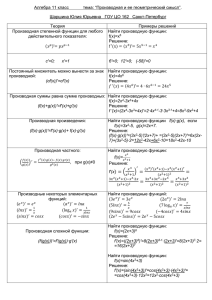
1 Муниципальное бюджетное общеобразовательное учреждение «Побединская средняя общеобразовательная школа» Томская область, Шегарский район п. Победа Модульно – блочная технология на уроках математики. Учитель математики Трубачева Светлана Владимировна. Высшая квалификационная категория 2 В «Концепции российского образования» подчеркивается: "Общеобразовательная школа должна формировать целостную систему универсальных знаний, умений, навыков, а также опыт самостоятельной деятельности и личной ответственности обучающихся, то есть ключевые компетентности, определяющие современное качество содержания образования". Компетенции по математике базовые математические приемы, алгоритмы измерений математический язык самостоятельная познавательная деятельность, основанная на усвоении способов приобретения математических знаний из различных источников информации математическая грамотность, т.е. необходимость вырабатывать у школьников способность определять и понимать роль математики в мире, в котором они живут; высказывать хорошо обоснованные математические суждения вырабатывать у учащихся умения применять математические знания и навыки в нестандартных ситуациях, умения, которые будут способствовать успешности выпускника во взрослой жизни Но для формирования данных компетенций необходимы особые дидактические условия. На первое место по значимости следует поставить разработку особой методической системы. Именно поэтому, значительное внимание уделяется внедрению новых педагогических технологий, одна из которых – модульное обучение. Задачи модульно - блочной технологии: - предоставление возможности самоопределения в выборе тем, методов, форм, направлений самостоятельной работы; - помощь в понятии личностной значимости конечного результата; - предоставление возможности самореализации в творчестве; - развитие навыка самоанализа и самооценки формируемой компетентности. -развитие у учащихся прочных, осознанных знаний и умений; -создание на уроках благоприятной психологической атмосферы, способствующей раскрытию личностного потенциала ребенка. Область применения: уроки математики Ожидаемые результаты: предполагается повышение познавательной активности, достижения прочности усвоения знаний, более высокий уровень сформированности основных математических компетенций. В 8 – 11 классах, вот уже несколько лет, я использую модульно - блочную технологию. Сущность модульно-блочного обучения состоит в том, что ученик полностью самостоятельно (или с определенной дозой помощи) достигает конкретных целей учения в процессе работы с модулем. Модульное обучение основано на следующей основной идее: ученик должен учиться сам, а учитель обязан осуществлять управление его учением: мотивировать, организовывать, 3 координировать, консультировать, контролировать. По мнению авторов данной технологии, оно интегрирует в себе все то - прогрессивное, что накоплено в педагогической теории и практике. Так, из программированного обучения заимствуется идея активности ученика в процессе его четких действий в определенной логике, постоянное подкрепление своих действий на основе самоконтроля, индивидуализированный темп учебнопознавательной деятельности. Из теории поэтапного формирования умственных действий используется самая ее суть - ориентировочная основа деятельности. Из психологии используется также рефлексивный подход. Накопленные обобщения теории и практики дифференциации, оптимизации обучения, проблемности - все это интегрируется в основах модульного обучения, в принципах и правилах его построения, отборе методов и форм осуществления процесса обучения. Средством модульного обучения выступает модуль, т.к. в него входит: целевой план действий, банк информации, методическое руководство по достижению дидактических целей. Именно модуль может выступать как программа обучения, индивидуализированная по содержанию, методам учения, уровню самостоятельности, темпу учебно-познавательной деятельности ученика. Ученик точно знает, что от него ожидается по завершении каждого этапа обучения, каким проверкам и экзаменам он будет подвергнут. Учебный материал должен быть хорошо иллюстрирован. Тестовая часть должна быть краткой, доступной. Набор учебных элементов предоставляет обучаемому сведения, необходимые для получения именно той профессиональной квалификации, которая соответствует его профессиональным целям. Учащийся может работать со своей собственной скоростью, постигая учебный материал в нужном ему объёме. На уроке ученик включен в процесс четких действий в определённой логике, подкреплённых самоконтролем, он самостоятельно или с помощью достигает конкретных целей учебно-познавательной деятельности в процессе работы с модулем. Высокая мотивация учащихся к процессу обучения за счёт того, что модуль гарантирует формирование именно той профессиональной подготовленности, которая потребуется впоследствии на рабочем месте. Меняется форма общения учителя и ученика, именно модули позволяют перевести обучение на субъект субъективную основу. Основные мотивы внедрения модульной технологии: - гарантированность достижения результатов обучения; - возможность выбора уровня обучения; - возможность обучения в индивидуальном темпе обучения; - возможность работы в парах, группах; - возможность самооценки, самокоррекции, самоконтроля, самообразования. При модульной технологии рекомендую использовать несколько правил: 1. Перед каждым модулем проводить входной контроль знаний и умений учащихся, чтобы иметь информацию об уровне готовности к работе по новому модулю. 4 2. При обнаружении пробелов в знаниях учащихся необходимо провести соответствующую коррекцию. 3. Обязательно осуществляется текущий и промежуточный контроль в конце каждого учебного элемента (чаще это мягкий контроль: самоконтроль, взаимоконтроль, сверка с образцом и т. д.). Текущий и промежуточный контроль имеют своей целью выявление пробелов в усвоении для их устранения непосредственно в ходе работы. 4. После завершения работы с модулем осуществляется выходной контроль, он должен показать уровень усвоения модуля. 5. Если итоговый контроль показал низкий уровень усвоения материала, необходимо проводить его доработку. 6. Введение модулей в учебный процесс нужно осуществлять постепенно. Необходимо сочетать традиционную систему обучения с модульной технологией. Очень хорошо вписываются в модульную систему обучения вся система методов, приемов и форм организации учебно-познавательной деятельности учащихся: работа индивидуальная, в паре, в группах. Модули можно вписывать в любую систему обучения и тем самым усиливать её качество и эффективность. Применение этой технологии позволяет мне излагать учебный материал крупными порциями и на этой основе высвободить время для повторения вопросов теории и решения задач. Дети заводят отдельно тетради для лекции (теории) по алгебре и геометрии. Это очень удобно при проведении повторения, подготовке к полугодовым и годовым контрольным работам и для подготовки к итоговой аттестации в 9 и 11 классах Весь учебный материал разбит на блоки, в которые включены несколько пунктов учебника. Материал этих пунктов можно изучать как единое целое, т. к. они опираются на одни свойства или математические формулы, либо законы. Можно пункты объединять, если одна тема является следствием другой темы В роли модуля конструкции блока уроков выступает здесь цикл уроков. Их расположение и количество в блоке может быть любым, но каждый цикл имеет жестко определенную структуру. 1 цикл: Урок - лекция. (Информационный модуль) Как правило, это один или два урока, на которых излагаю весь теоретический материал изучаемого блока. Изучение нового материала крупным массивом обязательно предваряется вводным повторением. На вводное повторение можно отвести время на лекции. Это объясняется большим разбросом среди учеников по мотивации, возможностям, уровням достижения. Чтобы процесс формирования и развития функциональной системы шел нормально, необходимо существующую функциональную систему актуализировать – загрузит в оперативную память учащихся те знания, умения и ценности, над которыми будут надстраиваться вновь изучаемые. 5 Учащимся выдается все содержание материала темы во всей системе внутренних и внешних связей, сопровождающихся примерами, историческими справками и образцами способов деятельности. Это делается в форме лекции и, следовательно, позволяет передать укрупненную дидактическую единицу. На основе фронтальной беседы с классом, привлекаю учащихся к объяснению отдельных этапов доказательства, изучению нового материала, тем самым выясняю, как воспринимаются вопросы теории. На протяжении всей лекции непрерывно слежу за процессом усвоения материала. С целью интенсификации учебного процесса на уроке использую технические средства обучения, различные таблицы, плакаты, ИКТ и др. В школе всегда есть значительный контингент учеников, которые по данной теме ограничиваются материалом, соответствующим образовательному стандарту, общеобразовательным минимумом. При изучении нового материала в начале блока внимание уделяется только общеобразовательному содержанию – основному объему. Достижению более эффективного конечного результата способствуют элементы первичного контроля: на следующем уроке провожу письменный или устный опрос по основным определениям и доказательствам. Если ученик не подготовился, или плохо подготовился к сдаче «теории», ее можно пересдать. Добиваюсь того, чтобы теорию сдал каждый ученик. 2 цикл: Уроки практических занятий. (Модуль систематизации) Затем следует объемная группа уроков, направленных на закрепление материала, отработку решения задач. Эти уроки называются уроки беседы или практикума. На уроках практических занятий провожу целенаправленную работу по выработке у учащихся умений и навыков решения задач. Образцы выполнения этих заданий учащиеся записывают обязательно в тетрадь. К доске вызываю слабых учеников, чтобы они лучше усвоили новый материал. К урокам в старших классах подбираю упражнения, которые позволяют параллельно с изучением нового, повторить некоторые общие подходы к решению задач из ранее изученного материала. Для более сильных ребят подбираю специальные задания повышенной трудности или увеличиваю объем решенных заданий. Таким образом, на уроках провожу дифференцированную работу с учащимися, с учетом интересов как сильных, так и более слабых из них. Этот элемент блока называется РДЗ – развивающее дифференцированное закрепление. На некоторых уроках провожу самостоятельные работы обучающего характера, с последующей проверкой. Уроки практикумы составляют 2/3 времени, отведенной на изучение этой темы. Обязательный материал немедленно отрабатываем на задачах и примерах, умение их решать должно быть отработано до автоматизма. Эта первая часть называется «тренинг – минимум». Успешность тренинга во многом определяется возможностью обеспечить каждому ученику: 6 - индивидуальный подбор задач - индивидуальный темп работы - полную самостоятельность выполнения работы - непрерывный контроль и управление. Прежде чем перейти к обучению на последующий уровень, требуется познакомить учеников с необходимой информацией дополнительного объема, обеспечивающей работу на общем и тем более продвинутом уровнях. В модульно – блочной технологии наличие достаточного времени для закрепления позволяет включить в систему проблемные задачи. Возможна даже проблемная лекция. В структуре блока уроков появляется еще один элемент изучения нового материала, предусматривающий активную познавательную деятельность школьников, в значительной мере самостоятельную. Изучение нового материала дополнительного объема: одни разбираются во всем, овладевают на уровне применения, другим полезно разобраться и понять идеи, третьим достаточно познакомиться. Кроме семинарских занятий, провожу уроки обобщения и систематизации, виде турниров, КВН, конференций, путешествий и т.д. 3 Цикл: Урок самостоятельной работы. (Модуль промежуточного контроля) На этом уроке провожу самостоятельную работу по карточкам, или дидактическим материалам, или тестирование. Цель самостоятельной работы – получение информации об успешности блока уроков. Вся эта информация используется на уроке коррекции и при доработке учебно-методического материала. Многие дети выполняют задания медленно, в силу сложившихся психотипов. Должны быть защитные механизмы, позволяющие в условиях действия жестких правил все-таки чувствовать себя комфортно и «медленным» ученикам. Защитный механизм заключается в том, что каждый ученик вправе пересдать (с целью повышения оценки) любую из ранее сданных тем, в физических границах учебного года. Количество попыток ограничено обычно ученик имеет право на одну такую попытку. Реализация этого права фиксируется в классном журнале или в моей собственной документации. 4 цикл: Уроки консультаций и коррекции знаний. (Модуль коррекции знаний) Когда блок уроков подходит к концу, возникает необходимость обобщающего повторения, которое позволило бы ученикам увидеть всю тему целиком, получить некое системное знание ее, понять свое собственное место в предметном поле. Консультация является одной из наиболее эффективных форм организации урока обобщающего повторения в преддверии тематического или итогового контроля. На этом уроке использую информацию проведенной самостоятельной работы. На уроке коррекции ученики могут объединиться в группы и сообща анализировать свои работы. Ученики, которые получили высший балл, могут на этом уроке работать с учителем, или решать нестандартные задачи, или помогать товарищам. 7 На уроках данного типа провожу целенаправленную работу по ликвидации пробелов в знаниях учащихся, концентрируя их внимание на главных и существенных моментах изучаемой темы. 5 Цикл: Контрольная работа. (Модуль контроля) На этом уроке осуществляется проверка знаний, умений и навыков учащихся, приобретенных ими в процессе изучения данной темы, а также связанных с ней предыдущих тем. Структура контрольного задания: 2 - 3 задания минимального уровня, 1 - 2 задания первого уровня, одно задание второго уровня. Все уровни явно выделены. Ученики обычно быстро понимают, что гарантировать себе нужную оценку можно, если потрудиться над домашним заданием после урока коррекции. Используемые методы обучения: - объяснительно – иллюстративный -эвристический - программированный Преобладающие организационные формы обучения: - беседа -практикум Основные средства диагностики: - текущие письменные опросы (тесты) -контрольные работы или зачеты по окончании изучения темы Эта технология мне очень нравится, удобна она и детям. Они уже знают всю последовательность проведения уроков, и это во многом облегчает мою работу. Список литературы: 1. Гареев В.М., Куликов С.И., Дурко Е.М. Принципы модульного обучения. — Вест.высш.шк., 1987. Н8, с. 35-38. 2. Полякова Н.В. Перспективные школьные технологии. — ЗАВУЧ, научно-практический журнал, 5, 2005. — с. 38-50. 3. Селевко Г.К. Современные образовательные технологии: Учебное пособие. — М.: Народное образование, 1998. —256 с. 4. Скоробогатова Г.Г. Проблемная, проектная, модульная и модульноблочная технология в работе учителя. М.: МИОО, 2002. — 69 с. 5. Третьяков П.И., Сенновский И.Б. Технология модульного обучения в школе. — М.: Новая школа, 1997. 6. Учителю о педагогической технологии. М., 1989. 7. Цявичене П.Ю. Теория и практика модульного обучения. Каунас. 1989. 8. Чошанов М.А. Гибкая технология проблемно-модульного обучения. -М.: Народное образование, 1996. 8 9 Тематическое планирование блока «Уравнения и неравенства», 10класс. № Содержание модулей. Блок № 3 Уравнения и неравенства Количество часов 46часов Информационный модуль 25 часов 1. Понятие уравнения и неравенства. Равносильные уравнения. 1 час 2. Показательные уравнения и неравенства. 4 часа 3. Логарифмические уравнения и неравенства. 4 часа 4. Иррациональные уравнения и неравенства. 4 часа 5. Тригонометрические уравнения и неравенства. 8 часов 6. Системы уравнений и неравенств. 4 часа Модуль систематизации 4 часа 1. Общие способы решения основных типов уравнений. 2 часа 2. Общие способы решения основных типов неравенств. 2 часа Модуль промежуточного контроля 5часов Самостоятельные работы 1) Показательные уравнения и неравенства. 1час 2) Логарифмические уравнения и неравенства. 1час 3) Иррациональные уравнения и неравенства. 1час 4) Тригонометрические уравнения и неравенства. 1час 5) Системы уравнений и неравенств. 1час Модуль коррекции знаний 4 часа 1. Работа над пробелами в знаниях и умениях при решения основных типов уравнений и неравенств. 2 часа 2. Решение нестандартных уравнений и неравенств. 2 часа Модуль контроля 8 часов 10 1. 2. Контрольные работы. 6 часов 1) Показательные уравнения и неравенства. 1 час 2) Логарифмические уравнения и неравенства. 1 час 3) Иррациональные уравнения и неравенства. 1 час 4) Тригонометрические уравнения и неравенства. 1 час 5) Системы уравнений и неравенств. 1 час 6) Релейная контрольная работа. 1 час Тест « Уравнения и неравенства» 2 часа 11 Приложение № 2 Карточки 6класс. Блок «Дроби» Правило Умножь 1) числитель 2) на числитель и 3) знаменатель на знаменатель . · = Умножение дробей. Примеры Задания 1) 2 1 3)4 4)1 5)1 6) 7) 8) 9) 10) 11) 12) 13) 14)2 Основное свойство дроби Правило Примеры Приведение дроби к Привести дробь к новому знаменателю: новому знаменателю 15. 1. Умножь (раздели) Решение: знаменатель 1. 3·5=15 дроби на число 2. 2·5=10 2. Умножь (раздели) Ответ: числитель дроби Привести дробь к на то же число 3. Запишите в ответе новому знаменателю 7. получившуюся Решение: дробь. 1. 14:2 =7 2. 8:2=4 Ответ: Задания Привести дроби к новому знаменателю 24. ; ; Привести дроби к новому знаменателю 7. ; ; Разделите числитель и знаменатель дроби на 2. ; ; Умножить числитель и знаменатель на 5. ; ; Сократите дробь: ; ; 12 Сравнение, сложение и вычитание дробей с разными знаменателями. Правило Примеры Задания 1. Привести дроби к Сравнить и . Найти 1) 2) наименьшему их сумму и разность. 3) 4) общему Наименьший общий 5) 6) знаменателю знаменатель 12. 2. Сравнить, сложить 7) 8) = = или вычесть 10) 9< 10, значит < , т.е. 9) получившиеся дроби с 11) 12) < одинаковыми 13) 14) + = + = =1 знаменателями. 15) - = - = Приложение №3 Урок консультация и коррекция знаний. (Модуль коррекции знаний) 13 Урок алгебры в 11 классе. Обучающая цель: способствовать усвоению формул и правил дифференцирования, геометрического смысла производной. Развивающая цель: развитие творческих способностей учащихся, формирование способности учащихся к фиксированию собственных затруднений в деятельности, выяснению их причин, построению и реализации проекта выхода из затруднений. Воспитательная цель: формирование коммуникативных качеств, навыков самооценки. Ход урока: 1. Самоопределение к деятельности (1-2 мин) Французский писатель Анатоль Франц заметил: «Что учиться можно только весело… Чтобы переварить знания, надо поглощать их с аппетитом.» Последуем совету писателя: будем на уроке активны, внимательны, будем «поглощать» знания с большим желанием, ведь очень скоро они вам понадобятся. Впереди у вас Единый Государственный экзамен. 2. Актуализация знаний и фиксация затруднения в деятельности (10мин) Работаем устно. Повторяем правила дифференцирования. - как найти производную от произведения - как найти производную от суммы - как найти производную от частного - уравнение касательной - геометрический смысл производной - физический смысл производной. 1. Найти производную функции: f(х) = 2х – 3 f(х) = х2 – 3х +4 f(х) = (2х + 1)2 f(х) = f(х) = f(х) = 3х4 – 7х3 + 2х2 + f(х) = х-3 + f(х) = +1 2.Известно, что угловой коэффициент касательной к графику функции в точке с абсциссой х0 равен 0,72. Чему равно значение производной в этой точке? 3.Касательная к графику функции у = f(х) в точке с абсциссой х0 образует с положительным направлением оси х угол 450. Найти f’ (х0) 4.На рисунке изображен график функции у = f(х) и касательная, проведенная к нему в точке с абсциссой х0. Найти значение производной в точке х0. 5. Дана функция f(х) = 2х2. Найти f \(-1) f\ (2) 6.Найти значение производной функции у = 3. Презентация проекта (10мин) при х = ; х = 0; х = - 14 Когда мы начали изучать производную, я задала вам вопрос: какая история у дифференциального исчисления? Как часто производная используется при решении задач? Вы на этот вопрос не смогли ответить, и тогда вам было предложено провести самостоятельное исследование. Сегодня на уроке вы предоставите нашему вниманию результат вашей деятельности. Итак свой проект представляет Гильд Эльвира. Теперь слово Поповой Карине. Огромное спасибо девочкам. За работу вы получаете пятерки в журнал. 4. Самостоятельная работа с самопроверкой (20мин) Эталон Вариант 1 1. Найти производную функции у = ех 1) ех 2) ех + 3) хех-1 4)хех-1 + у’=(ex)’ – (cosx)’= ех + Ответ: 2 2. Найти производную функции у = 1) 2) 4 3) 4) - y’= y’(1) = = = в точке х0=1 = = =- Ответ: 4 3. Найти производную функции у = хlnх 1) 1+ lnх 2) -1 + lnх 3) 1 4) 1- lnх y’= x’·(lnx) + x·(lnx)’=1· lnx + x· = lnх + 1 Ответ: 1 4. Записать уравнение касательной к графику функции f(х) = х3 – 2х в точке с абсциссой 2. 1) у =24-10х 2)у = 4х + 2 3) у = 10х – 16 4)у = 18 – 10х f(2) = 23 - 2· 2=8-4=4 f’(x) = (x3)’ – (2x)’=3x2 -2 f’(2) = 3·22 – 2=12-2=10 y=4+10(x-2) = 4 + 10x – 20 = 10x – 16 Ответ: 3 5. Точка движется по закону s(t) = t2 +t. Найти скорость и ускорение в момент времени t = 7. 1) 7и3 2)15 и 2 3)15 и 7 4) 8 и 9 υ(t) = s’(t) = 2t + 1 15 υ(7) = 2·7 + 1=15 a(t) = υ’(t) = (2t+1)’ = 2 Ответ: 2 Вариант 2 1. Найти производную функции у = х4 1)4х - 2) 4х3 - 3) 4х3 + 4) 4х + y’=(x4)’ – (x-1)’=4x3 - (- 1)·(x-2)=4x3 + Ответ: 3 2. Найти производную функции у = 1) 2) -1 3)0 4) 1 y’= y’(0) = = = = =1 Ответ: 4 3. Найти производную функции у = ех 1)1 2) 2 в точке х0=0 при х0 = 3) 0 4) y’=(ex)’·sinx + ex(sinx)’ = ex·sinx + ex·cosx = ex(sinx + cosx) y’( = ·( + ) = Ответ: 4 4. Записать уравнение касательной к графику функции f(х) = 4х2 + 1 в точке с абсциссой -2. 1)у = -16х - 15 2)у = 16х + 49 3) у = 17х + 18 4)у = 18 – 10х f(-2) = 4·(-2)2 +1 = 4·4 +1= 17 f’(x) = (4x2 +1)’ = 4·2х = 8х f’(-2) = 8·(-2) = -16 y = 17 + (-16)(х-(-2)) = 17 - 16х - 32 = -16х – 15 Ответ: 1 5. Точка движется по закону s(t) = 3t2. Найти скорость и ускорение в момент времени t = 3. 1)7 и 3 2)15 и 2 3)15 и 7 4) 18 и 6 υ(t) =s’(t) = 3·2t = 6t υ(3) = 6·3 = 18 a(t) = υ’(t) = (6t)’ = 6 Ответ: 4 Вариант 3 1. Найти производную функции у = 12х3 - ех 1) 15х2 - хех-1 2)36х2 - хех-1 3)3х2 4)36х2 - ех 16 y’=(12x3)’ – (ex)’ = 12·3x2 – ex = 36x2 - ex Ответ: 4 2. Найти производную функции у = в точке х0 = 0 1)1 2) 0 3)16 4) y’= y’(0) = = = = =1 Ответ: 1 3. Найти производную функции у = (х2 +1)(х3 –х) при х0 = 1 1)0 2) 2 3) -2 4) 4 5 3 3 y= x + x – x –x = x5 - x y’=(x5 - x)’ = 5x4 – 1 y’(1) = 5·1 – 1 = 4 Ответ: 4 4. Записать уравнение касательной к графику функции f(х) = х2 +3х в точке с абсциссой 2. 1)у =7х – 4 2)у = 4х + 2 3) у = 10х – 16 4)у = 18 – 10х f(2) = (2)2 +3·2 = 4 + 6 = 10 f’(x) = (x2 +3x)’ = 2х + 3 f’(2) = 2·2 + 3 = 7 y = 10 + 7(x-2) = 10 + 7x – 14 = 7x - 4 Ответ: 1 5. Точка движется по закону s(t) = 0,1t2. Найти скорость и ускорение в момент времени t = 20. 1)7 и 0,3 2)15 и 0,2 3)15 и 0,7 4) 4 и 0,2 υ(t) =s’(t) = 0,1·2t = 0,2t υ(20) = 0,2·20 = 4 a(t) = υ’(t) = (0,2t)’ = 0,2 Ответ: 4 Вариант 4 1. Найти производную функции у = ех – 3х5 1) ех – 15х4 2) ех – 5х4 3)1 - 15х4 4)ех - х6 у’=(ex)’ – (3х5)’ = ех – 15х4 Ответ: 1 2. Найти производную функции у = 1) -1 2) 1 3)0 4) 2 y’= = в точке х0 = 0 = 17 y’(0)= = =1 Ответ: 2 3. Найти производную функции у = (t4 – 3)(t2 + 2) в точке t0 = 1 1) -8 2) 8 3) 6 4) -6 у = t6 - 3t2 + 2t4 – 6 y’ = 6t5 - 6t + 8t3 y’(1) = 6·1 - 6·1 + 8·1 = 8 Ответ: 2 4. Записать уравнение касательной к графику функции f(х) =2х3 – 5 в точке с абсциссой -2. 1) у = 27+ 24х 2)у = 4х + 2 3) у = 10х – 16 4)у = 18 – 10х f(-2) = 2·(-2)3 – 5= -16 – 5 = -21 f’(x) = (2x3 -5)’ = 2·3x2 = 6x2 f’(-2) = 6·(-2)2 = 24 y=-21 + 24(x+2) = -21 +24x + 48 = 24x + 27 Ответ: 1 5. Точка движется по закону s(t) = момент времени t = 5. 1) 7и3 2)5 и 1 3)15 и 7 . Найти скорость и ускорение в 4) 8 и 9 υ(t) = s’(t) = ( t2)’ = ·2t = t υ(5) = 5 a(t) = υ’(t) = (t)’ = 1 Ответ: 2 Дополнительное задание. С1 Найти абсциссы всех точек графика функции f(х) = 2х3 касательные в которых параллельны прямой у = 23х или совпадают с ней. 5.Рефлексия Проверяем, выставляем себе оценку. Находим ошибки, сверяя с эталоном. Берут карточки, где есть ошибки и прорешивают. «Дорогу осилит идущий» Домашнее задание: составить карточку для товарища и порешать ее самому. Карточки для самостоятельной работы. Вариант 1 1. Найти производную функции у = ех 1)ех 2) ех + 3) хех-1 4)хех-1 + 2. Найти производную функции у = в точке х0 = 1 1) 2) 4 3) 4) 3. Найти производную функции у = хlnх 1)1+ lnх 2) -1 + lnх 3) 1 4) 1- lnх 18 4. Записать уравнение касательной к графику функции f(х) = х3 – 2х в точке с абсциссой 2. 1)у =24-10х 2)у = 4х + 2 3) у = 10х – 16 4)у = 18 – 10х 5. Точка движется по закону s(t) = t2 +t. Найти скорость и ускорение в момент времени t = 7. 1)7 и 3 2)15 и 2 3)15 и 7 4) 8 и 9 Вариант 2 1. Найти производную функции у = х4 1)4х - 2) 4х3 - 3) 4х3 + 4) 4х + 2. Найти производную функции у = 1) 3. в точке х0 = 0 2) -1 3)0 4) 1 Найти производную функции у = ех при х0 = 1)1 2) 2 3) 0 4) 4. Записать уравнение касательной к графику функции f(х) = 4х2 + 1 в точке с абсциссой -2. 1)у =-16х - 15 2)у = 16х + 49 3) у = 17х + 18 4)у = 18 – 10х 5. Точка движется по закону s(t) = 3t2. Найти скорость и ускорение в момент времени t = 3. 1)7 и 3 2)15 и 2 3)15 и 7 4) 18 и 6 Вариант 3 1. Найти производную функции у = 12х3 - ех 1)15х2 - хех-1 2)36х2 - хех-1 3)3х2 4)36х2 - ех 2. Найти производную функции у = в точке х0 = 0 1)1 2) 0 3)16 4) 3. Найти производную функции у = (х2 +1)(х3 –х) при х0 = 1 1)0 2) 2 3) -2 4) 4 4. Записать уравнение касательной к графику функции f(х) = х2 +3х в точке с абсциссой 2. 1)у =7х – 4 2)у = 4х + 2 3) у = 10х – 16 4)у = 18 – 10х 5. Точка движется по закону s(t) = 0,1t2. Найти скорость и ускорение в момент времени t = 20. 1)7 и 0,3 2)15 и 0,2 3)15 и 0,7 4) 4 и 0,2 Вариант 4 1. Найти производную функции у = ех – 3х5 1)ех – 15х4 2) ех – 5х4 3)1- 15х4 4)ех - х6 2. Найти производную функции у = в точке х0 = 0 1)-1 2) 1 3)0 4) 2 3. Найти производную функции у = (t4 – 3)(t2 +2) в точке t0 = 1 1)-8 2) 8 3) 6 4) -6 19 4. Записать уравнение касательной к графику функции f(х) =2х3 – 5 в точке с абсциссой -2. 1)у =27+ 24х 2)у = 4х + 2 3) у = 10х – 16 4)у = 18 – 10х 5. Точка движется по закону s(t) = . Найти скорость и ускорение в момент времени t = 5. 1)7 и 3 2)5 и 1 3)15 и 7 4) 8 и 9 Карточки для дополнительного задания, в тех примерах, где есть ошибки. Карточка 1 1. Найти производную функции у = ех 1) ех 2) ех + 3) хех-1 4)хех-1 + 2. Найти производную функции у = х4 1)4х - 2) 4х3 3) 4х3 + 4) 4х + 3. Найти производную функции у = 12х3 - ех 1) 15х2 - хех-1 2)36х2 - хех-1 3)3х2 4)36х2 - ех 4. Найти производную функции у = ех – 3х5 1) ех – 15х4 2) ех – 5х4 3)1 - 15х4 4)ех - х6 Карточка 2 1. Найти производную функции у = в точке х0=1 1) 2) 4 3) 4) - 2. Найти производную функции у = 1) 2) -1 3)0 4) 1 3. Найти производную функции у = 1)1 в точке х0 = 0 в точке х0 = 0 2) 0 3)16 4) 4. Найти производную функции у = 1) -1 2) 1 3)0 4) 2 в точке х0 = 0 Карточка 3 1. Найти производную функции у = ех при х0 = 1)1 2) 2 3) 0 4) 2. Найти производную функции у = ех при х0 = 1)1 2) 2 3) 0 4) 3. Найти производную функции у = (х2 +1)(х3 –х) при х0 = 1 1)0 2) 2 3) -2 4) 4 4.Найти производную функции у = (t4 – 3)(t2 +2) в точке t0 = 1 1) -8 2) 8 3) 6 4) -6 Карточка 4 20 1. Записать уравнение касательной к графику функции f(х) = х3 – 2х в точке с абсциссой 2. 1)у =24 - 10х 2)у = 4х + 2 3) у = 10х – 16 4)у = 18 – 10х 2. Записать уравнение касательной к графику функции f(х) = 4х2 + 1 в точке с абсциссой -2. 1)у =-16х - 15 2)у = 16х + 49 3) у = 17х + 18 4)у = 18 – 10х 3. Записать уравнение касательной к графику функции f(х) = х2 + 3х в точке с абсциссой 2. 1)у =7х – 4 2)у = 4х + 2 3) у = 10х – 16 4)у = 18 – 10х 4. Записать уравнение касательной к графику функции f(х) =2х3 – 5 в точке с абсциссой -2. 1) у = 27 + 24х 2)у = 4х + 2 3) у = 10х – 16 4)у = 18 – 10х Карточка 5 1. Точка движется по закону s(t) = t2 + t. Найти скорость и ускорение в момент времени t = 7. 1)7 и 3 2)15 и 2 3)15 и 7 4) 8 и 9 2. Точка движется по закону s(t) = 3t2. Найти скорость и ускорение в момент времени t = 3. 1)7 и 3 2)15 и 2 3)15 и 7 4) 18 и 6 2 3. Точка движется по закону s(t) = 0,1t . Найти скорость и ускорение в момент времени t = 20. 1)7 и 0,3 2)15 и 0,2 3)15 и 0,7 4) 4 и 0,2 4.Точка движется по закону s(t) = . Найти скорость и ускорение в момент времени t = 5. 1) 7 и 3 2)5 и 1 3)15 и 7 4) 8 и 9