Введение в моделирование

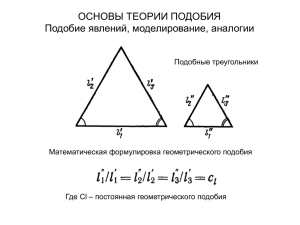
ЛЕКЦИЯ 1
Вопросы:
Краткая характеристика курса, история
его создания. Применение математических
методов и ЭВМ в народном хозяйстве. Значение моделирования в исследованиях, оптимизации и управлении технологическими
процессами. Краткий исторический очерк
развития моделирования как метода исследования механико-технологических процессов
текстильной промышленности. Цели и задачи
курса. Содержание понятий "модель" и "моделирование". Виды моделирования: физическое и математическое. Теория подобия - основа физического моделирования. Основные
теоремы теории подобия.
В этом году вы приступаете к изучению
новой технической дисциплины "Моделирование технологических процессов". История
ее начинается формально со 2-го апреля 1975
года, когда Учебно-методическим управлением по высшему образованию при министерстве высшего и среднего специального образования СССР была утверждена программа
этого курса для высших учебных заведений
по четырем специальностям к которым относятся и две ваши. Программу этого курса составил д.т.н. Севостьянов Алексей Григорьевич. Заслуга его в деле введения данного курса в группу дисциплин, преподаваемых в текстильных ВУЗах, состоит не только в том,
что он , будучи в возрасте 65 лет смог разработать качественно новый предмет, но
главным образом в том, что первым сумел
рассмотреть ту тенденцию в развитии и совершенствовании высшего образования, которая возникла благодаря созданию новых
технических средств исследования явлений и
объектов в сфере промышленной технологии.
В настоящее время ведущими специалистами
по "Моделированию технологических процессов текстильного производства" является
коллектив кафедры "Механической технологии волокнистых материалов" Московского
Ордена Трудового Красного Знамени текстильного института возглавляемого проф.
Севостьяновым А.Г. При кафедре создана лаборатория "Математических методов исследования механико-технических процессов",
оснащенная современными приборами и
средствами электронно-вычислительной техники. Работа по усовершенствованию курса
"Моделирование технологических процессов"
совершается в настоящее время максимальными темпами. Наши с вами усилия мы будем рассматривать как составную часть этой
большой работы.
При проектировании или совершенствовании технологических процессов и объектов
возникают многочисленные задачи, требующие исследования количественных и качественных закономерностей изменении их во
времени. Для решения этих задач используются как расчетные, так и экспериментальные методы. Однако применение натурального эксперимента, то есть эксперимента на реальном объекте, во многих случаях невозможно либо из-за его длительности, либо изза непреодолимых организационных и техни-
ческих трудностей. Эти обстоятельства требуют обогащения арсенала методов исследования, не связанных с проведением натуральных экспериментов. К таким методам относится метод моделирования.
Значительную роль метод моделирования играет при решении задач, связанных с
автоматизацией управления. Результаты моделирования позволяют вскрыть закономерности процесса, существенные с точки зрения
автоматизированного управления, обосновано выбрать алгоритм управления. По данным
моделирования может быть оценена эффективность различных принципов управления, вариантов построения управляющих систем, а также работоспособность и надежность управляющих устройств.
Большим преимуществом моделирования является то, что затраты рабочего времени и материальных средств на реализацию
моделей оказываются значительными по
сравнению с затратами, связанными с натуральным экспериментом. Вместе с тем результаты моделирования, как правило, близки
к результатам натурного эксперимента, что
превращает моделирование в эффективный
метод научного исследования. Изучение новой дисциплины начнем с выделения двух
ключевых моментов в картине общего технического прогресса цивилизации.
Технические достижения человечества
за последние полстолетия феноменальны.
Выделить среди них наиболее важные затруднительно, но все же два достижения мы
можем смело отнести к разряду выдающихся.
Первое заключается в изобретении техноло-
гического оборудования, на котором из сырья
под действием энергии вырабатываются
огромные количества специализированных
видов продукции. В ачестве примеров можно
назвать такие отрасли промышленности, как
электронная, машиностроительная, текстильная и многие, другие.
Другое выдающееся достижение - электронные вычислительные машины. Их изобретение часто сравнивают по воздействию на
технический прогресс о промышленной революцией. За период, немногим более десятилетия, ЭВМ усовершенствованы настолько,
что их арифметические и логические возможности могут быть использованы для
управления, обеспечивающего эффективное
проведение современных сложных процессов. Вычислительные машины, приспособленные для этой цели, служат основой вычислительных и автоматизированных систем
управления технологическими процессами.
Создание универсальных вычислительных машин привело к математизации целого
ряда наук, далеких в недавнем прошлом от
какого--либо влияния математических методов: экономики, медицины, педагогики,
лингвистики, теории искусства.
Вообще говоря, установление количественных связей между объектами является
главной и высшей задачей любого научного
исследования В этой связи нельзя не вспомнить знаменитое высказывание К. Маркса:
"Любая наука только тогда достигает совершенства, когда ей удается воспользоваться
математикой".
В настоящее время математизация
научного и практического знания является
господствующей тенденцией. Использование
больших возможностей конкретного количественного анализа изучаемых явлений - такова задача сейчас не только, исследователя, но
и инженера. Вот почему обучение методам
научного исследования с применением ЭВМ
технологических явлений ставится задачей
дня.
В курсе "Моделирование технологических процессов" (МТП), как подсказывает
само название, исследование рассматривается
как связанное с построением подходящей модели. Принципиальная особенность этих моделей состоит в том, что эти модели являются
динамическими, то есть описывающими изменение во времени исследуемого параметра.
Поясним это на примере. Возьмем рассматривавшуюся вами зависимость длины нити в
петле l от глубины кулирования hk и натяжения Т провязываемой нити в форме полинома
1-ой степени,
l = b 0 x 1+ b 1 + b 1 x 2
где
x1 
h k  h ko
T  T0
x

; 2
h
T
hk0; Т0 - глубина кулирования и натяжения нити на нулевом (основном) уровне
h; T - интервалы варьирования;
b0 , b1, b2 – постоянные коэффициенты,
определяемые теоретически или экспериментально.
Эта модель статическая. С ее помощью
невозможно исследовать такой, например,
вопрос, как влияние колебаний
входного натяжения провязываемой нити
на длину нити в петле. Очевидно, что статическая модель лишь в среднем описывает
данную зависимость. В общем случае:
l  Фhk ( t ); T ( t )
Это выражение, содержит параметр t - время
и характеризует уже временную связь между
l; hk и T.
В
курсе
"Моделирование
технологических процессов" изучаются статические и динамические модели.
Цели изучения дисциплины состоят
в изучении научных, технических, методических
основ моделирования и оптимизации
технологических процессов в текстильной и
легкой промышленности.
Задачи изучения дисциплины
Основными задачами дисциплины в области моделирования являются
изучение
его видов, их особенностей и методик построения соответствующих моделей; в области оптимизации – изучение методов решения однокритериальных и многокритериальных задач оптимизации.
В результате изучения дисциплины сту-
дент должен иметь представление:
 о моделировании как методе исследования
технологических процессов в текстильной
и легкой промышленности и его теоретических основах;
 о видах моделирования, их достоинствах и
недостатках;
 о методах построения математических моделей,
реализуемых
на
персональных
ЭВМ;
 о моделировании случайных процессов;
 о динамических характеристиках объектов
и методах их определения;
 о задачах оптимизации и их специфике;
 об однокритериальных задачах оптимизации;
 о многокритериальных задачах оптимизации;
 о подходах к решению однокритериальных
и многокритериальных задачах оптимизации;
должен знать:
 методику проведения анализа размерностей при исследовании технологических
процессов;
 алгоритмы
построения
математических
моделей случайных процессов;
 алгоритмы имитационного моделирования
технологических объектов;
 методы определения динамических характеристик объектов;
 методы решения однокритериальных и
многокритериальных задач оптимизации;
должен уметь использовать:
 методы математического моделирования
для исследования технологических процессов в текстильной и легкой промышленности;
 методы решения однокритериальных и
многокритериальных задач оптимизации;
должен владеть:
 методами построения и анализа математических моделей технологических процессов и объектов;
 методами решения однокритериальных и
многокритериальных задач оптимизации.
Моделирование
Обобщенно моделирование есть метод
опосредованного познания, при котором для
получения информации об изучаемом явления исследуется некоторый вспомогательный
искусственный или естественный объект (модель), имеющий определенное объективное
соответствие с изучаемым объектом (оригиналом) и заменяющий оригинал на некоторых
этапах исследования.
По существу моделирование есть особая форма эксперимента. В обычном эксперименте средства экспериментального исследования взаимодействуют непосредственно с самим объектом исследования.
При моделирований такого прямого контакта
нет. Здесь экспериментируют не с самим
объектом, а с его заменителем, который и
называют моделью.
Философский базис моделирования
Цель изучения мира - познание его законов. Закон есть прочное (остающееся) в явлении. Закон = спокойное отражение явлений. Закон существенное явление.
Закон и сущность - понятия однородные
и одностепенные, выражающие углубление
познания человеком явлений мира. Явление
богаче закона.
(В.И. Ленин, "Философские тетради",
Москва, 1973 г. стр. 133-148)
В настоящее время моделирование становится общим методом научных исследований.
При
исследование
механикотехнологических процессов текстильного
производства наибольшее распространение
имеют физическое и математическое моделирование.
Физическое моделирование
Характеризуется тем, что исследование
объектов проводится на стендах, установках,
макетах, сохраняющих в той или иной степени физическую природу изучаемых процессов и моделей. Физическое моделирование имеет следующие достоинства:
1. Более полное по сравнению с математическим моделированием воспроизведение
свойств исследуемого процесса или объекта.
2. Исследование процесса более простое
в сравнение с исследованием на реальном
объекте.
Недостатки:
1. Метод менее универсален, т.к. при
изменении параметров исследуемого объекта
или при воспроизведении нового объекта необходимо переделывать старую или создавать новую модель, что обусловливает большие затраты времени и средств.
2. Относительно высокая стоимость
модели сложных объектов.
Математическое моделирование
При математическом моделировании
исследование технологических процессов ведется на модели, имеющей физическую природу, отличную от природы объекта.
Метод математического моделирования
основан на идентичности математических
описаний процессов, протекающих в моделируемой системе и в моделирующей. На принципе аналогии уравнений основано использование ЭВМ, позволяющих моделировать раз-
личные процессы природы процессами в
электрических цепях.
Математическое моделирование включает два основных этапа:
1. Математическое описание процесса, т.е.
получение математической модели.
2. Исследование этой модели на аналоговой
или цифровой ЭВМ.
Известны три вида математического моделирования:
1. Моделирование с помощью моделей прямой
аналогии
В этом случае устанавливается непосредственная взаимосвязь между основными
параметрами, которые характеризуют процессы различной природы. Примеры прямой
аналогии:
перенос тепла вдоль проводника:
q
dT
dx
(1)
перенос электрических зарядов по проводнику:
i
1 dU
 dx
(2)
По форме уравнения (1) и (2) идентичны.
Другой пример прямой аналогии:
загрузка бункера  накопление зарядов в
электрическом конденсаторе
Такой вид моделирования является
наиболее простым. Модели прямой аналогии
строятся только для специализированных
применений и не могут решать любую задачу.
2. Моделирование с помощью моделей
непрямой аналогии
Используются для моделирования вычислительной машины и при исследовании уравнений математических операций сложения,
умножения, интегрирования различными
электронными решающими устройствами,
схемы соединения которых соответствуют,
структуре самих уравнений.
В связи с несовершенством применяемых решающих устройств в АВМ (дрейф нуля усилит, пост, тока УПТ), нестабильность
параметров деталей и т.п. а также погрешности измерений снижают точность решения
уравнений, т.е. точность результатов на АВМ
ниже, чем на НВМ.
Однако при исследовании многих механико-технологических процессов не требуется высокая точность решений (исходные данные имеют малую точность). Поэтому для
решения многих задач; выгодно применять
простые недорогие АВМ, которых отличает:
1. быстродействие;
2. наглядность;
3. удобство сопоставления;
4. интерпретация результатов
5. получение решений в реальном масштабе времени или в любом другом масштабе.
АВМ проще агрегировать с измеритель-
ными устройствами, которые устанавливаются непосредственно на реальном объекте или
на физической модели. При моделировании
на АВМ не требуется трудоемкого специального программирования.
3. Цифровое моделирование
Исследование моделей распадается на
ряд отдельных арифметических действий с
параметрами процесса, которые представляются в виде дискретных значений, изображаемых
числами. Это позволяет применять ЦВМ.
Действия с цифрами наряду с логическими операциями осуществляются на
ЭЦВМ. Точность ЭЦВМ значительно выше
АВМ. Они более надежны, имеют более широкие возможности.
Математическое моделирование в сочетании с современными вычислительными
машинами позволяют при относительно небольших материальных затратах исследовать
различные варианты технологических режимов объекта, конструктивного оформления
машин с целью оптимизации решения.
Математическое моделирование в сочетании с физическим ускоряет изучение
свойств процесса (объекта) и расширяет возможности установления адекватных закономерностей процесса.
Если полное математическое описание
процесса отсутствует, то этот случай типичен
для решения кибернетических задач, когда
при наличии неполной информации об объекте осуществляется параллельно создание
математической модели и ее исследование.
При кибернетическом моделировании используется модель черного ящика.
Теоретической основой моделирования является теория подобия, одной из задач
которой - установление зависимостей между
параметрами процессов, протекающих в объекте и модели, иными словами, выбор масштабов для модели, при которых эти процессы будут подобными. Если же объект и модель подобны, то информация о поведении
объекта в заданных условиях может быть получена при исследовании модели в подобных
условиях.
Теоремы теории подобия
Эксперимент - краеугольный камень познания, метод исследования, при помощи которого проверяется справедливость гипотез,
загадок, моделей, устанавливаются значения
ряда коэффициентов и показателей.
Теория подобия является “грамматикой”
эксперимента и моделирования. Она указывает, как нужно ставить опыт, обрабатывать
опытные данные, а также обобщать и распространять полученные результаты на другие
объекты.
Становление теории подобия в историческом аспекте характеризует ее теоремы:
1-я теорема: "Подобные системы имеют одинаковые критерии подобия. Критерии
подобия - это безразмерные выражения, составленные из параметров, характеризующих
процесс или объект.
Анализ размерностей - метод поиска
критериев.
2-я теорема: (π-теорема). Состоит в доказательстве возможности сведения уравнения, описывающего процесс или объект, к
критериальному виду. ( Э. Букингем, 1914
год).
3-я теорема: Подобны те явления, которые имеют одинаковые определяющие
критерии.
3-я теорема определяет пределы распространения результатов единичного опыта.
Теория подобия - связующее звено между теорией и экспериментом.
СУЩНОСТЬ ТЕХНИЧЕСКОГО МОДЕЛИРОВАНИЯ И
КОНСТРУИРОВАНИЯ
§ 1. МОДЕЛИ И МОДЕЛИРОВАНИЕ
Слово «модель» (от лат. modulus — мера, образец) имеет несколько смысловых оттенков и
используется во многих областях науки, техники, производства, обучения. В широком смысле
— это условный образ (изображение, схема,
описание и т. п.) какого-либо объекта (или системы объектов), процесса или явления.
В научных исследованиях под моделью понимают
такую мысленно представленную или материально
реализованную систему, которая, отображая или
воспроизводя объект исследования, способна замещать его так, что ее изучение дает нам новую
информацию об этом объекте'.
В обучении модели применяются как одно из
средств наглядности. Они могут быть объектами
трудовой деятельности (предметами изготовления) и способствовать воспитанию интереса у
школьников к определенному виду техники и развитию у них технических способностей.
Модели различных сооружений люди начали строить очень давно. Однако при этом они часто учитывали только геометрическое соотношение отдельных частей модели и реального объекта, не
принимая во внимание различных физических явлений, связанных, например, с использованием неодинаковых материалов для их постройки. Это
было причиной многих неудач, катастроф. Постепенно усилиями многих ученых была создана тео-
рия подобия, которая рассматривает подобие физических явлений.
Одним из первых применил теорию подобия при
постройке модели арочного моста русский изобретатель И. П. Кулибин. Он установил, что при
изменении масштаба деталей условия работы их
меняются непропорционально. Например, при изме1
Штофф В. А. Моделирование и философия. М.—Л., 1966.
нении линейных размеров модели в k раз собственный вес ее изменяется в k s раз, а площадь
поперечных сечений элементов— в k2 раз; модели
в l/k натуральной величины имеют напряжения от
собственного веса в k раз меньше, чем напряжения в оригиналах.
Теория подобия применяется при постройке моделей технических устройств и инженерных сооружений. При этом модель испытывается в условиях, близких к тем, в которых будет работать
спроектированный объект. Полученные результаты
используются при постройке объекта. Такой подход в технике получил широкое распространение и
стал называться моделированием. Мастерски делали модели отечественные изобретатели И. П. Кулибин, А. Н. Крылов, Д. И. Журавский, В.А.Дектярев и многие другие творцы техники.
Моделирование есть метод исследования сложных технических устройств, сооружений или процессов на их моделях одинаковой или различной
физической природы с применением теории подобия при постановке эксперимента и обработке его
результатов.
Потребность в моделировании возникает тогда,
когда непосредственное исследование самого объекта затруднительно, дорого или требует больших
затрат времени. В зависимости от характера замещаемого процесса или объекта различают прямое моделирование и метод аналогии.
П р я м о е м о д е л и р о в а н и е основано на замещении изучаемого физического процесса подобным ему процессом той же физической природы и
применяется при изучении сравнительно простых
систем, например гидравлических, тепловых в
случае движения однофазных сред и т. п. Все
крупные гидростанции, такие, как Асуанская,
Братская, Волгоградская, Сая-но-Щушенская, Нурекская и другие, при проектировании исследовались в искусственно созданных руслах и
водоемах на моделях, изображающих в уменьшенном масштабе эти грандиозные сооружения.
Метод а н а л о г и и используют при изучении
более сложных систем, например, электрических, живых организмов и других, а также производственных и технологических процессов. При
этом замещают изучаемые физические, химические,
психологические и другие процессы подобными им
процессами другой природы. Исследование проводят с помощью специальных моделей, построенных
на идентичности математического описания оригинала (объекта) и модели.
Следует отметить, однако, что теория подобия и основанное на ней моделирование не отражают с абсолютной полнотой все стороны и детали изучаемых явлений.
На практике применяют три способа моделирования: полное, неполное и приближенное. При
п о л н о м м о д е л и р о в а н и и процессы, характеризующие изучаемые явления, подобно
12
изменяются и во времени, и в пространстве. При
н е п о л н о м м о д е л и р о в а н и и процессы, характеризующие изучаемое явление, подобны частично. В
п р и б л и ж е н н о м м о д е л и р о в а н и и между некоторыми параметрами систем или некоторыми параметрами их режимов не существует соотношений
подобия.
С точки зрения соответствия физической природы подобных явлений различают два вида подобия:
физическое и математическое. Физическое подобие существует при одинаковой физической природе подобных явлений. Это значит, что механическим процессам в прототипе должны соответствовать механические процессы в подобной ему
модели, электрическим процессам— электрические и
т. д. Математическое подобие предполагает лишь
соответствие параметров технического устройства и модели.
В технических задачах обычно выделяют еще и
частные виды физического подобия. Так, о подобии движения тел говорят как о кинематическом
подобии,
подобие
масс
отдельных
частей
устройства называется материальным подобием, а
подобие сил — динамическим. Технические устройства, подобные кинематически, материально и динамически, называют м е х а н и ч е с к и
подобными.
Модели могут быть материальными (изготовленными из конструкционных материалов) и идеальными (существующими в воображении).
К последним можно отнести условно графические изображения: схемы, чертежи, технические
рисунки и т. п.
Материальные модели в зависимости от того,
как они отображают изучаемые объекты, делят
на группы.
Пространственно подобные модели характеризуются геометрическим подобием по отношению к
изучаемому объекту. Это макеты домов, застройки поселков и городов, инструментов и
приспособлений, географические макеты; биологические муляжи; модели кристаллов, молекул и т.
п.; компоновки (расположение оборудования в
кабинетах, мастерских, цехах).
Физически подобные модели — это модели плотин, кораблей, самолетов, ракет, механизмов и
узлов машин и т. п.; модели, замещающие один
вид
живых
организмов
другим,
более
распространенным в биологических исследованиях,
и др.
Математические подобные модели отличаются от
изучаемого объекта физической природой, а отношение между изучаемым объектом и моделью выражается аналогией. Это аналоговые модели — аналоговые вычислительные машины (АВМ), электрические модели механических, тепловых, биологических процессов и т. п.; цифровые вычислительные машины (ЦВМ), различные кибернетические
устройства.
Особую группу материальных моделей составляют
т р е н а жеры. Их применяют для формирования
навыков в управле4 ■>
нии сложными объектами и машинами. Физическая модель здесь сочетается
с реальными приборами. Воздействие на эти приборы преобразуется в импульсы, моделирующие поведение управляемого объекта. Так, тренажеры для летчиков, управляющих вертолетами, воспроизводят у обучаемого все физические ощущения, связанные с полетом в любом направлении, подъемом и спуском вертолета.
Термин
«моделирование»,
который
широко
применяется
во
внеклассной
работе
по
технике,
не
имеет
непосредственного
отношения
к
моделированию
как
ме^ду
научного
познания.
Изготовление
моделей
на
занятиях
является
одним
из
наиболее
распространенных
видов
приобщения
учащихся
различных>озрастных
групп
к
творческой
деятельности
в
области
техники.
А^для
многих
это
прикладной
технический
вид^
спорта.
Модели
технических
объектов,
изготавливаемые
учащимися
на
уроках
технического
труда,
вноклаоопых
эанптпях
или-дома,
обычно
называют
техническими.
По
назначению
они
делятся
на
модели—наглядные
пособия
и
спортивно-технические.
При
пост
ройке
моделей—
наглядных
пособий
основное
вниманиеобращают
на
принцип
действия
прототипа.
При
этом
не
так
важно
добиться
внешнего
сходства,
как
воспроизвести
внутреннее
уст
ройство.
Например,
модель
автомобиля
должна
иметь
двига
тель, сцепление, коробку передач, рулевое управление и т. п. При
постройке
спортивных
моделей
стремятся
к
тому,
чтобы
они
либо
развивали
максимальную
скорость,
либо
перемещались
на
большое
расстояние,
либо
поднимали
или
перемещали
определенный
груз
на
заданное
расстояние
и
т.
п.
Спортивные
модели
могут
быть
кордовыми
(авиа-,
судо-),
стендовыми
(автои
судо-),
с
Дистанционным
управлением
и
свободно
пе
ремещающимися.
<
Технические модели в зависимости от того, как они отображают объект,
можно разделить на модели-копии и обобщенные модели. Модели-копии отражают либо геометрическое подобие прототипа (образца), либо его физическую
сущность.Они имеют внешнее сходство (форму и цвет) с прототипом, содержат большинство узлов, органы управления, двигательную установку с источником питания и могут перемещаться. Обобщенные модели не обязательно
должны быть похожи по внешнему виду на прототип. Они отражают основные
признаки и свойства всего класса представляемых ими машин, механизмов,
сборочных единиц (узлов) и т. п. ^«Апример, модели винтовой передачи,
дифференциала и др.).
Модели могут быть динамическими (действующими) и статическими, (не действующими).
Учащиеся строят модели по имеющимся чертежам или прототипу, применяя
при этом прямое моделирование и основываясь на неполном или приближенном
подобии. Задавшись масштабным коэффициентом Я, по формулам пересчитывают па-
раметры прототипа на модель. Например, линейные размеры модели по
сравнению с прототипом уменьшают в К раз, т. е.
где LM — линейный размер детали модели или модели в целом; Ln — линейный
размер аналогичной детали или прототипа. Такие параметры модели, как
скорость движения, мощность двигательной установки, площадь конкретной детали и т. п., определяют по иным формулам. Об этом будет сказано
во втором разделе.