1 курс дисциплина «Математика

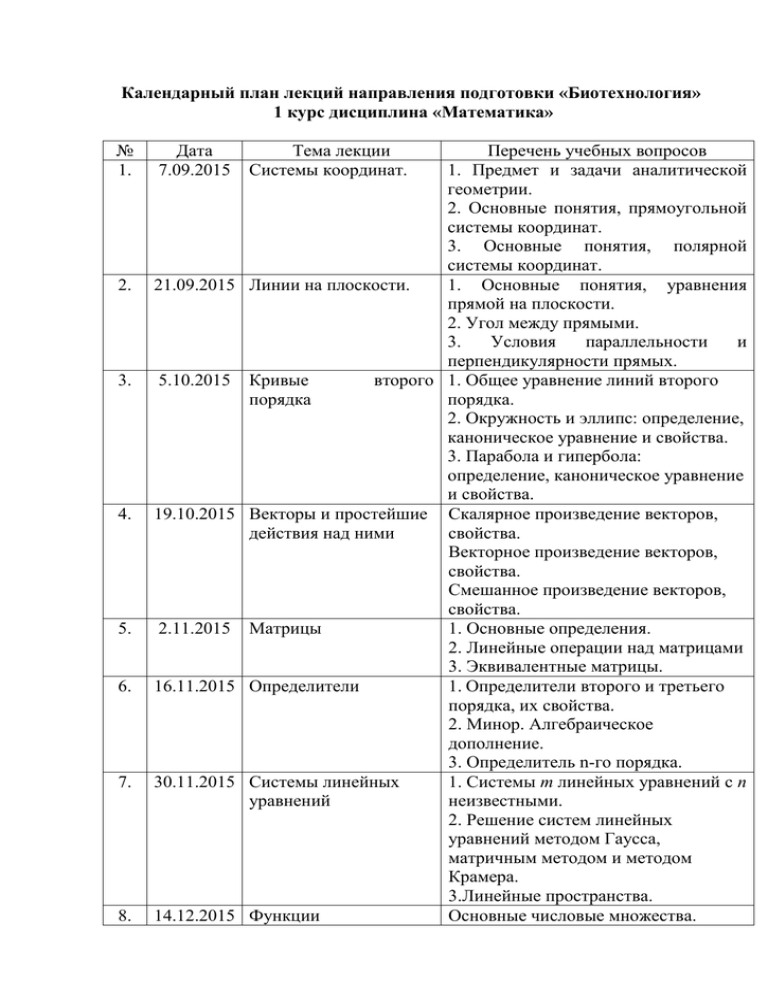
Календарный план лекций направления подготовки «Биотехнология»
1 курс дисциплина «Математика»
№
1.
Дата
7.09.2015
Тема лекции
Системы координат.
2.
21.09.2015 Линии на плоскости.
3.
5.10.2015
4.
19.10.2015 Векторы и простейшие1.
действия над ними
2.
Кривые
порядка
второго
3.
Матрицы
5.
2.11.2015
6.
16.11.2015 Определители
7.
30.11.2015 Системы линейных
уравнений
8.
14.12.2015 Функции
1.
Перечень учебных вопросов
1. Предмет и задачи аналитической
геометрии.
2. Основные понятия, прямоугольной
системы координат.
3. Основные понятия, полярной
системы координат.
1. Основные понятия, уравнения
прямой на плоскости.
2. Угол между прямыми.
3.
Условия
параллельности
и
перпендикулярности прямых.
1. Общее уравнение линий второго
порядка.
2. Окружность и эллипс: определение,
каноническое уравнение и свойства.
3. Парабола и гипербола:
определение, каноническое уравнение
и свойства.
Скалярное произведение векторов,
свойства.
Векторное произведение векторов,
свойства.
Смешанное произведение векторов,
свойства.
1. Основные определения.
2. Линейные операции над матрицами
3. Эквивалентные матрицы.
1. Определители второго и третьего
порядка, их свойства.
2. Минор. Алгебраическое
дополнение.
3. Определитель n-го порядка.
1. Системы m линейных уравнений с n
неизвестными.
2. Решение систем линейных
уравнений методом Гаусса,
матричным методом и методом
Крамера.
3.Линейные пространства.
Основные числовые множества.
9.
28.12.2015 Предел
последовательности
Функции одной переменной.
2. Основные элементарные функции, их
графики.
3. Сложная функция.
1. Последовательности, предел
числовой последовательности.
2. Теоремы о пределах.
3. Признаки существования пределов.
Календарный план лекций направления подготовки «Биотехнология»
2 курс дисциплина «Математика»
№
1.
Дата
2.09.2015
Тема лекции
Элементы
комбинаторики
2.
16.09.2015 Элементы теории
множеств
3.
30.09.2015 Элементы теории
вероятностей
4.
14.10.2015 Элементы теории
вероятностей
5.
28.10.2015 Случайные величины
6.
11.11.2015 Законы распределения
случайных величин
7.
25.11.2015 Элементы
математической
статистики
Перечень учебных вопросов
1. Основные задачи, решаемые
дискретной математикой.
2. Формулы комбинаторики.
3. Правила комбинаторики.
1. Основные определения теории
множеств.
2. Действия над множествами.
3. Отношения, свойства бинарных
отношений;
отношения
эквивалентности и порядка.
1.
Пространство
элементарных
событий.
2. Алгебра событий.
3. Классическое и статистическое
определение вероятности.
1. Условные вероятности,
независимые события.
2. Формулы полной вероятности и
Байеса.
3. Повторение испытаний, формула
Бернулли.
1. Непрерывные и дискретные
случайные величины.
2. Функции распределения случайных
величин, их свойства.
3. Основные характеристики
случайных величин.
1. Геометрическое и биномиальное
распределения.
2. Распределение Пуассона,
распределение Стьюдента.
3. Показательное и нормальное
распределения.
1. Основные задачи математической
статистики.
2. Точечные оценки параметров
распределения, их характеристики
(несмещенность,
эффективность,
состоятельность).
3. Интервальные оценки параметров.
8.
9.12.2015
Элементы
математической
статистики
1. Постановка и методы решения
задачи
проверки
статистических
гипотез.
2. Проверка гипотез о значениях
параметров
нормального
распределения.
Тематический план практических занятий направления подготовки
«Биотехнология» 1 курс дисциплина «Математика»
№
1.
2.
3.
4.
5.
6.
7.
Кол-во
Тема занятия
Перечень учебных вопросов
часов
2
Система координат на 1. Декартова прямоугольная и полярная
плоскости
системы координат на плоскости.
2. Простейшие задачи на плоскости.
3. Уравнение прямой на плоскости.
4
Плоскость и прямая в 1. Плоскость.
пространстве
2. Прямая в пространстве.
3. Основные задачи на плоскость и
прямую в пространстве.
4
Кривые
второго 1.
Окружность:
определение,
порядка
каноническое уравнение и свойства.
2. Эллипс: определение, каноническое
уравнение и свойства.
3.
Гипербола:
определение,
каноническое уравнение и свойства.
4.
Парабола:
определение,
каноническое уравнение и свойства.
4
Элементы
векторной 1. Понятие вектора.
алгебры
2. Линейные операции над векторами.
3.
Нелинейные
операции
над
векторами.
4
Матрицы
и 1. Матрицы и действия над ними.
определители
2. Нахождение обратной матрицы.
3. Определители.
4. Минор и алгебраические дополнения.
6
Системы
линейных 1. Матричная запись систем линейных
уравнений
уравнений.
2. Решение систем линейных уравнений
методом Гаусса.
3. Решение систем линейных уравнений
матричным методом.
4. Решение систем линейных уравнений
методом Крамера.
4
Нахождение пределов 1. Основные элементарные функции.
числовых
2. Теоремы о пределах. Признаки
последовательностей
существования пределов.
3. Нахождение пределов числовых
последовательностей.
8.
4
9.
4
Нахождение
функций
пределов 1. Бесконечно малые и бесконечно
большие величины.
2. Предел функции.
3. Сравнение бесконечно малых
величин.
4. Первый и второй замечательный
пределы.
5. Раскрытие неопределенностей.
Непрерывность
1. Понятие непрерывности функции.
функций
2. Точки
разрыва. Классификация
точек разрыва.
3. Теоремы о непрерывных функциях
на отрезке.
4.
Непрерывность
элементарных
функций.
Тематический план практических занятий направления подготовки
«Биотехнология» 2 курс дисциплина «Математика»
№
1.
Кол-во
Тема занятия
часов
4
Элементы дискретной
математики
2.
4
Элементы теории
множеств
3.
4
Основы теории
вероятностей
4.
4
Основные теоремы
теории вероятностей
5.
4
Дискретные случайные
величины
6.
4
Непрерывные
случайные величины
7.
2
Законы распределения
случайных величин
Перечень учебных вопросов
1. Основные задачи дискретной
математики.
2. Основные формулы комбинаторики.
3.
Сочетания,
перестановки
и
размещения с повторениями.
4. Правила комбинаторики.
1. Множества. Основные операции над
множествами.
2. Бинарные отношения.
3. Свойства бинарных отношений.
4. Отношения эквивалентности и
порядка.
1. Виды случайных событий.
2. Полная группа событий.
3. Статистическая и математическая
вероятности.
4. Границы изменения вероятностей.
1. Теоремы сложения вероятностей.
2. Условная вероятность.
3. Теоремы умножения вероятностей.
4. Формула полной вероятности.
5. Формула Бернулли
6. Теорема гипотез (формула Байеса).
1. Понятие дискретной случайной
величины.
2. Способы задания дискретных
случайных величин.
3.
Основные
характеристики
дискретных случайных величин.
1. Понятие непрерывной случайной
величины.
2. Интегральная и дифференциальная
функции распределения, их свойства.
3.
Основные
характеристики
непрерывных случайных величин.
1. Геометрическое и биномиальное
распределения.
8.
4
Основные понятия
математической
статистики
9.
2
Определение
доверительного
интервала
2.
Распределение
Пуассона,
распределение Стьюдента.
3.
Показательное
и
нормальное
распределения.
1. Задачи, решаемые математической
статистикой.
2. Выборочный
метод. Простой
статистический ряд.
3.
Статистическое
распределение
выборки, гистограмма, многоугольник
распределения.
4. Точечные оценки параметров
распределения, их характеристики
(несмещенность,
эффективность,
состоятельность). Метод наибольшего
правдоподобия.
1. Интервальные оценки параметров.
2. Доверительный интервалы для
математического
ожидания
нормального распределения.
3. Постановка и методы решения задачи
проверки статистических гипотез.