КОНТРОЛЬНАЯ РАБОТА работе (независимо от ее качества), признается неудовлетворительной.

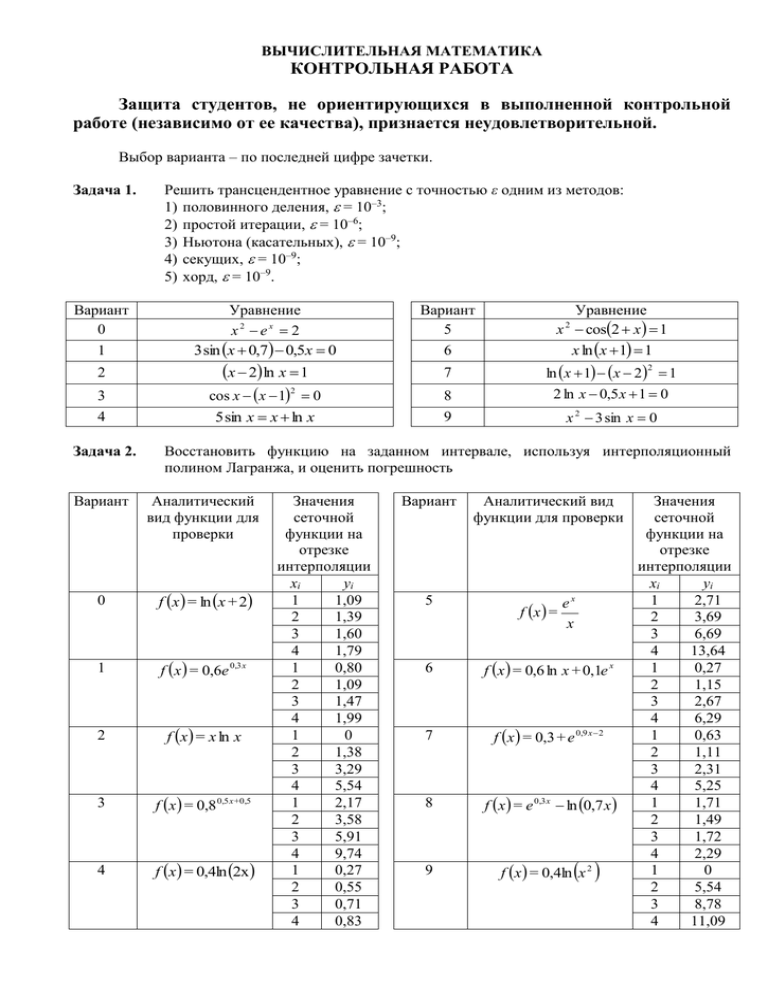
ВЫЧИСЛИТЕЛЬНАЯ МАТЕМАТИКА
КОНТРОЛЬНАЯ РАБОТА
Защита студентов, не ориентирующихся в выполненной контрольной
работе (независимо от ее качества), признается неудовлетворительной.
Выбор варианта – по последней цифре зачетки.
Задача 1.
Вариант
0
1
2
3
4
Задача 2.
Вариант
Решить трансцендентное уравнение с точностью ε одним из методов:
1) половинного деления,  = 10–3;
2) простой итерации,  = 10–6;
3) Ньютона (касательных),  = 10–9;
4) секущих,  = 10–9;
5) хорд,  = 10–9.
Уравнение
x2  ex  2
3 sin x  0,7  0,5x  0
x  2 ln x  1
2
cos x  x  1  0
Вариант
5
6
7
8
9
5 sin x  x  ln x
Уравнение
x  cos2  x   1
x ln x  1  1
2
ln  x  1  x  2  1
2
2 ln x  0,5 x  1  0
x 2  3 sin x  0
Восстановить функцию на заданном интервале, используя интерполяционный
полином Лагранжа, и оценить погрешность
Аналитический
вид функции для
проверки
0
f x  = ln x + 2
1
f x  = 0,6e 0,3 x
2
f x = x ln x
3
f x  = 0,8 0,5 x+0,5
4
f x = 0,4ln 2x 
Значения
сеточной
функции на
отрезке
интерполяции
xi
yi
1
1,09
2
1,39
3
1,60
4
1,79
1
0,80
2
1,09
3
1,47
4
1,99
1
0
2
1,38
3
3,29
4
5,54
1
2,17
2
3,58
3
5,91
4
9,74
1
0,27
2
0,55
3
0,71
4
0,83
Вариант
5
Аналитический вид
функции для проверки
f x  =
ex
x
6
f x  = 0,6 ln x + 0,1e x
7
f x  = 0,3 + e 0,9 x  2
8
f x  = e 0,3 x  ln 0,7 x 
9
f x  = 0,4ln x 2
 
Значения
сеточной
функции на
отрезке
интерполяции
xi
yi
1
2,71
2
3,69
3
6,69
4
13,64
1
0,27
2
1,15
3
2,67
4
6,29
1
0,63
2
1,11
3
2,31
4
5,25
1
1,71
2
1,49
3
1,72
4
2,29
1
0
2
5,54
3
8,78
4
11,09
ВЫЧИСЛИТЕЛЬНАЯ МАТЕМАТИКА
КОНТРОЛЬНАЯ РАБОТА
Задача 3.
С точностью ε = 0,0001 приблизиться к точке минимума (максимума) целевой
функции
F  Ax12  Bx 22  Cx1  Dx 2  M
методом Гаусса – Зейделя, начиная движение от точки x1( 0 ) = 0, x 2( 0 ) = 0
A
3
-4
4
-2
2
Вариант 0 min
Вариант 1 max
Вариант 2 min
Вариант 3 max
Вариант 4 min
Задача 4.
B
2
-3
3
-4
3
0
3
sin x
2 x dx
Вариант
5
1
интеграл
D
-12
24
6
16
-18
M
31
-50
42
-45
33
Вариант 5
Вариант 6
Вариант 7
Вариант 8
Вариант 9
A
-2
4
-3
3
-3
max
min
max
min
max
B
-3
2
-4
4
-2
C
12
-32
6
-12
16
D
12
-4
24
-32
4
M
-29
68
-36
90
-24
Вычислить приближенное значение интеграла с точностью ε = 0,0001 одним из
методов:
1) по формуле прямоугольников;
2) по формуле трапеций;
3) по формуле Симпсона.
Для проверки вычислить точное значение интеграла по формуле Ньютона-Лейбница.
Вариант
интеграл
C
-12
8
-24
16
-4
x
 cos xdx
0
1
2
1
 cos x
4
2
dx
2 ln x
dx
0
6
dx
0,5 sin x 2
1
3
2
e
dx
 1+ ln x
1
dx
0
7
2
 x2
4
3

1+ ln x dx
1
8
3
dx
 x+e
0
9
1,5
x

0
cos x
dx
x +1
ВЫЧИСЛИТЕЛЬНАЯ МАТЕМАТИКА
ВОПРОСЫ ДЛЯ ПОДГОТОВКИ К ЗАЧЕТУ/ЭКЗАМЕНУ
ТЕМА 1 Основы теории погрешностей
1.
2.
3.
4.
5.
Устранимая и неустранимая погрешности математического моделирования.
Приближенные числа, их абсолютные и относительные погрешности.
Погрешности арифметических операций.
Прямая задача теории погрешностей (погрешности вычисления значений функции).
Обратная задача теории погрешностей (определение допустимой погрешности аргументов по
допустимой погрешности функции).
ТЕМА 2 Численные методы нахождения корней нелинейных уравнений с одним неизвестным
1.
2.
Методы отделения корней уравнения: графический способ, аналитический способ.
Методы уточнения приближенных корней: метод дихотомии (половинного деления), метод
хорд, метод Ньютона (касательных), метод секущих, метод простых итераций.
ТЕМА 3 Численное решение систем уравнений
1.
2.
3.
Точные методы решения систем линейных уравнений: метод Гаусса, метод Холецкого, метод
прогонки.
Итерационные методы решения систем линейных уравнений: метод Якоби, метод Зейделя.
Численное решение систем нелинейных уравнений: метод Ньютона, метод простой итерации.
ТЕМА 4 Приближение функций
1.
2.
3.
4.
5.
6.
Постановка задачи интерполирования.
Полиномиальная интерполяция: интерполяционные формулы Ньютона, интерполяционный
многочлен Лагранжа. Оценка погрешности интерполяции.
Интерполирование функций сплайнами (кусочно-полиномиальная интерполяция). Оценка
погрешности интерполирования кубическими сплайнами.
Обратное интерполирование.
Аппроксимация функций методом наименьших квадратов.
Равномерное приближение функций.
ТЕМА 5 Численные методы оптимизации
1.
2.
3.
4.
5.
Методы одномерной безусловной оптимизации: метод половинного деления, метод золотого
сечения, метод Фибоначчи, метод Пауэлла, метод секущих, метод касательной. Метод
случайного поиска.
Методы многомерной безусловной оптимизации нулевого порядка: метод прямого поиска
(метод Хука-Дживса), метод деформируемого многогранника (метод Нелдера-Мида), метод
вращающихся координат (метод Розенброка), метод параллельных касательных (метод
Пауэлла).
Методы многомерной безусловной оптимизации первого порядка: метод градиентного спуска,
метод наискорейшего спуска, метод наискорейшего покоординатного спуска (метод ГауссаЗейделя), метод сопряженных градиентов.
Методы многомерной безусловной оптимизации второго порядка: метод Ньютона, метод
Ньютона-Рафсона.
Методы условной оптимизации: метод множителей Лагранжа (аналитический метод), методы
штрафных и барьерных функций (использование двойственности).
ТЕМА 6 Численное дифференцирование
1.
2.
Некорректность
операции
численного
дифференцирования.
Формулы
численного
дифференцирования.
Погрешности, возникающие при численном дифференцировании (погрешность усечения и
погрешность округления) и их оценка.
ВЫЧИСЛИТЕЛЬНАЯ МАТЕМАТИКА
ТЕМА 7 Численное интегрирование
1.
2.
3.
Численное интегрирование на основе формул Ньютона-Котеса: формула прямоугольников,
формула трапеций, формула Симпсона (формула парабол), формула Ньютона.
Методы статистических испытаний (методы Монте-Карло).
Численное интегрирование на основе метода Гаусса.
ТЕМА 8 Численное решение дифференциальных уравнений
1.
2.
3.
4.
Аналитические приближенные методы решения задачи Коши: метод последовательного
дифференцирования, метод неопределенных коэффициентов, метод последовательных
приближений.
Численные методы решения задачи Коши. Разностные схемы: метод Эйлера, симметричная
схема, метод Адамса.
Численные методы решения задачи Коши. Методы Рунге-Кутта.
Методы решения краевой задачи Коши: метод стрельбы, метод конечных разностей, метод
прогонки.
ЛИТЕРАТУРА
1. Копченова Н. В., Марон И. А. Вычислительная математика в примерах и задачах: Учебное
пособие – СПб.: Изд-во «Лань», 2008.
2. Бахвалов Н. С., Жидков Н. П., Кобельков Г. М. Численные методы. Лаборатория Базовых
Знаний, 2003.
3. Вержбицкий В. М. Основы численных методов. – М.: Высшая школа, 2002.
4. Вержбицкий В. М. Численные методы (линейная алгебра и нелинейные уравнения). – М.:
ОНИКС 21 век, 2005.
5. Вержбицкий В. М. Численные методы (математический анализ и обыкновенные
дифференциальные уравнения). – М.: Высшая школа, 2001.
6. Численные методы – http://solidbase.karelia.ru/edu/meth_calc/files/vved.shtm
7. Введение в вычислительную математику –
http://www.exponenta.ru/educat/class/courses/student/courses.asp
8. Основы численных методов –
http://www.tgspa.ru/info/education/faculties/ffi/ito/programm/osn_chm/index.htm
9. Численные методы – http://mathserfer.com/theory.php?tema=chmeth
10. Трифонов А. Г. Постановка задачи оптимизации и численные методы ее решения –
http://matlab.exponenta.ru/optimiz/book_2/index.php
11. Методы оптимизации систем автоматизированного проектирования – http://www.optimizaciyasapr.narod.ru/
12. Кафедра математической кибернетики МАИ: материалы по оптимизации и численным методам –
http://www.dep805.ru/education/sessia.php
13. Он-лайн
решение
обыкновенных
дифференциальных
уравнений
–
http://alexlarin.net/Chmethods/duint.html
14. Ахмеров Р. Р. Численные методы решения обыкновенных дифференциальных уравнений –
http://www.nsc.ru/rus/textbooks/akhmerov/index.html
15. Тарасевич Ю. Ю.
Численные
методы
на
Mathcad'е
–
http://www.exponenta.ru/educat/systemat/tarasevich/default.asp
16. Алексеева Е. В., Кутненко О. А., Плясунов А. В. Численные методы оптимизации: Учеб.
Пособие/Новосиб.
ун-т,
Новосибирск,
2008.
–
http://www.math.nsc.ru/LBRT/k5/Plyasunov/Posobie3.pdf
17.