Численные методы механики сплошных сред

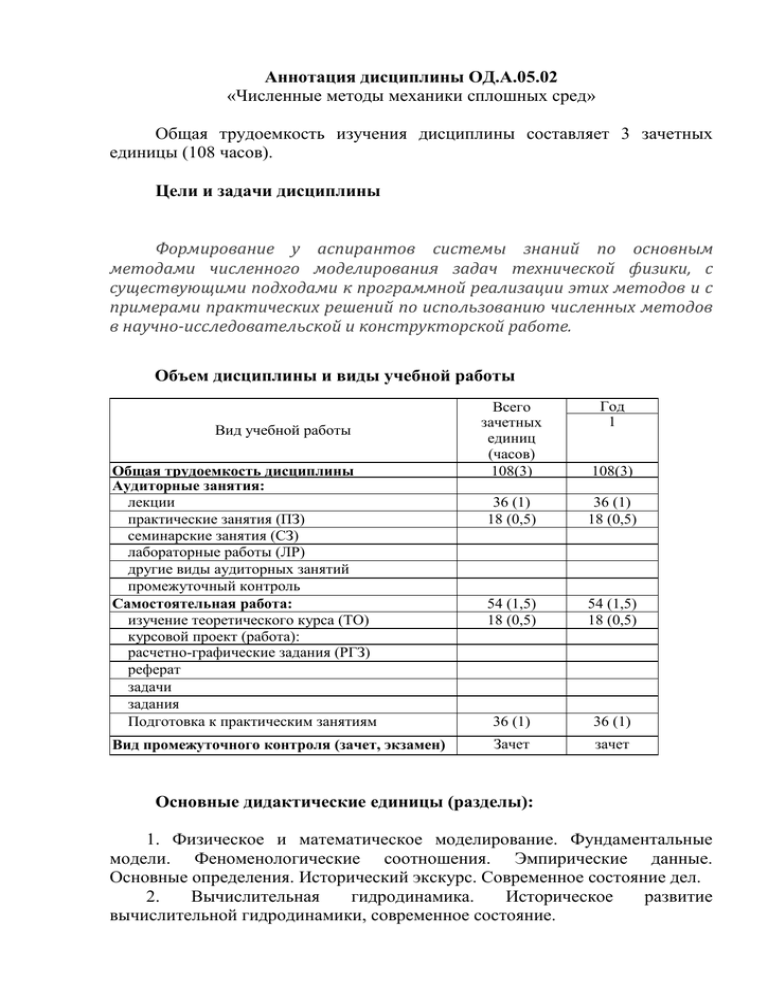
Аннотация дисциплины ОД.А.05.02
«Численные методы механики сплошных сред»
Общая трудоемкость изучения дисциплины составляет 3 зачетных
единицы (108 часов).
Цели и задачи дисциплины
Формирование у аспирантов системы знаний по основным
методами численного моделирования задач технической физики, с
существующими подходами к программной реализации этих методов и с
примерами практических решений по использованию численных методов
в научно-исследовательской и конструкторской работе.
Объем дисциплины и виды учебной работы
Вид учебной работы
Общая трудоемкость дисциплины
Аудиторные занятия:
лекции
практические занятия (ПЗ)
семинарские занятия (СЗ)
лабораторные работы (ЛР)
другие виды аудиторных занятий
промежуточный контроль
Самостоятельная работа:
изучение теоретического курса (ТО)
курсовой проект (работа):
расчетно-графические задания (РГЗ)
реферат
задачи
задания
Подготовка к практическим занятиям
Вид промежуточного контроля (зачет, экзамен)
Всего
зачетных
единиц
(часов)
108(3)
Год
1
обучения
36 (1)
18 (0,5)
36 (1)
18 (0,5)
54 (1,5)
18 (0,5)
54 (1,5)
18 (0,5)
36 (1)
36 (1)
Зачет
зачет
108(3)
Основные дидактические единицы (разделы):
1. Физическое и математическое моделирование. Фундаментальные
модели. Феноменологические соотношения. Эмпирические данные.
Основные определения. Исторический экскурс. Современное состояние дел.
2.
Вычислительная
гидродинамика.
Историческое
развитие
вычислительной гидродинамики, современное состояние.
3.Основные приближения, используемые при формулировании моделей
сплошной среды: идеальная среда, несжимаемая среда, изотермическая
среда, однокомпонентная среда, однофазная среда.
4. Обобщенное уравнение переноса. Конвективные и диффузионные
потоки. Описание физических процессов при помощи уравнений переноса.
Граничные условия уравнений переноса. Условия первого, второго рода,
смешанные условия. Физические границы и граничные условия на них.
Условия на твердой стенке, на плоскости симметрии, на входной и выходной
границе.
5.Моделирование течений с теплообменом. Моделирование течений со
свободной конвекцией. Основные подходы и приближения.
6. Моделирование задач с фазовым переходом (кристаллизацияплавление).
7. Методы моделирования течений жидкости со свободной
поверхностью. Лагранжевы методы. Эйлеровы методы. Level set и VOF
методы.
8. Методы моделирования течений жидкости с подвижными твердыми
телами. Immersed boundary method (IBM). Использование подвижной
системы
координат,
cкользящие
сетки,
динамические
сетки,
перекрывающиеся сетки.
9. Особенности турбулентных течений. Этапы развития моделирования
турбулентности. Методы описания структуры турбулентных течений.
Подход Рейнольдса. RANS модели турбулентности.
10. Однопараметрические модели турбулентности. Модель СпаллартаАлмареса.
Модели
с
двумя
дифференциальными
уравнениями
(двухпараметрические модели). Стандартная k-ε модель ее модификации.
Модели
с
двумя
дифференциальными
уравнениями
(двухпараметрические модели). SST модель.
11. Структура пристеночной области турбулентного течения. Метод
пристеночных функций. Законы стенки.
12. Прямое численное моделирование (DNS), его область применения,
ограничения применимости. Метод с выделением крупных вихрей (LES).
Метод моделирования отсоединенных вихрей (DES).
13. Моделирование задач аэроакустики. Основные методы расчета
акустических течений, их достоинства и недостатки. FHW – методика
расчета акустических течений. Описание методики, достоинства и
ограничения.
14. Моделирования задач с двухфазных сред. Лагранжев и эйлеров
метод расчета движения двухфазных сред.
15. Модели горения: кинетическая, гибридная и модель обрыва вихря
(EBU).Основные подходы их достоинства и ограничения.
16. Методы и подходы моделирования задач электродинамики
сплошных сред. Магнитная гидродинамика. Современные пакеты программ
для решения задач электродинамики.
17. Сетевые методы в гидродинамике. Область применения, достоинства
и ограничения.
18. Пакеты
теплообмена.
программ
для
вычислительной
гидродинамики
и
В результате изучения дисциплины аспирант должен:
Знать: формулировки основных фундаментальных физических законов
и их основные следствия применительно к задачам механики и
электродинамики сплошных сред, основные численные подходы, методы и
алгоритмы реализации моделей теплофизических процессов, существующие
программные комплексы для решения задач МСС.
Уметь: формулировать математические модели физических процессов
применительно к конкретных промышленным устройствам и технологиям,
проводить математическое моделирование этих процессов с помощью
соответствующих программ расчета на ЭВМ, корректно анализировать
результаты расчетов.
Владеть: навыками численного моделирования физических процессов,
протекающих в конкретных технических системах; разработки программ
расчета на ЭВМ на основе известных методов моделирования.