Расчет блока составной конструкции из ... круговой цилиндрической оболочки под действием ...
реклама
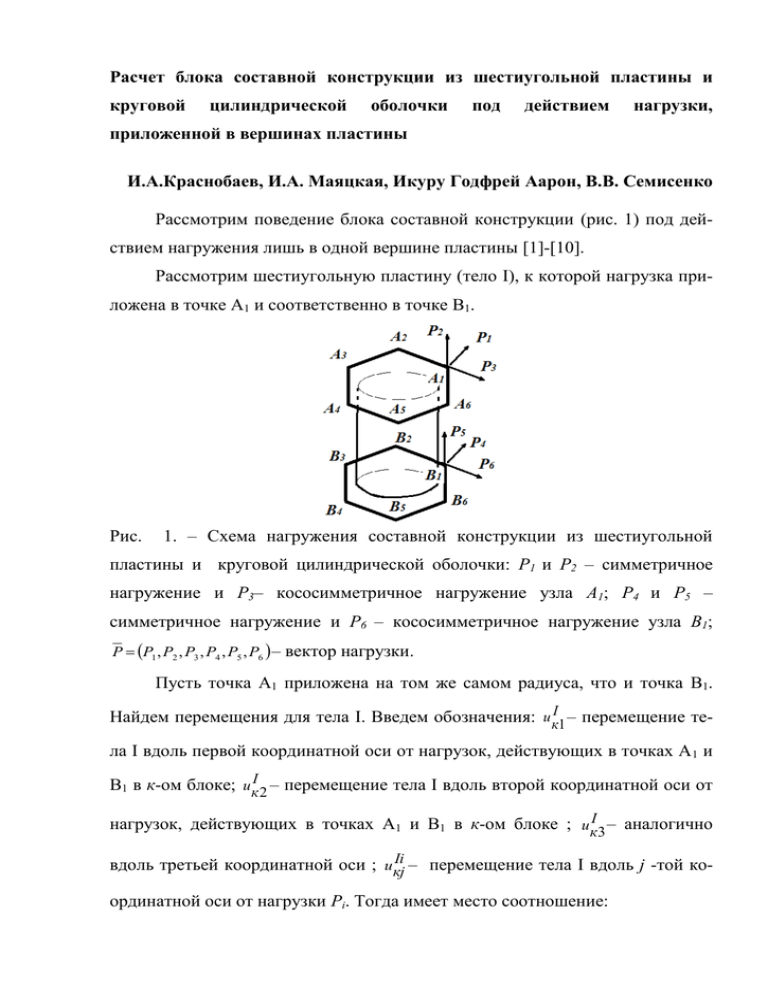
Расчет блока составной конструкции из шестиугольной пластины и круговой цилиндрической оболочки под действием нагрузки, приложенной в вершинах пластины И.А.Краснобаев, И.А. Маяцкая, Икуру Годфрей Аарон, В.В. Семисенко Рассмотрим поведение блока составной конструкции (рис. 1) под действием нагружения лишь в одной вершине пластины [1]-[10]. Рассмотрим шестиугольную пластину (тело I), к которой нагрузка приложена в точке А1 и соответственно в точке В1. Рис. 1. – Схема нагружения составной конструкции из шестиугольной пластины и круговой цилиндрической оболочки: Р1 и Р2 – симметричное нагружение и Р3– кососимметричное нагружение узла А1; Р4 и Р5 – симметричное нагружение и Р6 – кососимметричное нагружение узла В1; Р Р1 , Р2 , Р3 , Р4 , Р5 , Р6 – вектор нагрузки. Пусть точка А1 приложена на том же самом радиуса, что и точка В1. Найдем перемещения для тела I. Введем обозначения: u кI1 – перемещение тела I вдоль первой координатной оси от нагрузок, действующих в точках А 1 и В1 в к-ом блоке; u кI 2 – перемещение тела I вдоль второй координатной оси от нагрузок, действующих в точках А1 и В1 в к-ом блоке ; uкI 3 – аналогично Ii – перемещение тела I вдоль j -той ковдоль третьей координатной оси ; uкj ординатной оси от нагрузки Рi. Тогда имеет место соотношение: u кI1 u кI11 u кI12 u кI13 u кI14 u кI15 u кI16 ; I4 I5 I6 u кI 2 u кI12 u кI 22 u кI 3 2 uк 2 uк 2 uк 2 ; uкI 3 uкI13 uкI 32 uкI 33 uкI 34 uкI 35 uкI 36 ; ( i 1,2,...,6; j 1,2,3 ). (1) Ii и коэффициенты а Ii , полученные Введем аппроксимирующие функции Фкj kj после решения системы уравнений([8]–[9]): П l М ni l а ni l N ni l Pi 0 , kj kj kj k ni акj ,rs (2) где n I , II , III – номер тела; l 1– номер нагружения пары соответствующих вершин; i 1,2,...6 – номер нагружения; k 1,2,... – номер блока; j 1,2,3 – номер координатной оси. Ii и а Ii ([8]–[9]): Выразим перемещения через функции Фкj kj I1 Ф I1а I1 ; u кj кj kj I 3 Ф I 3а I 3 ; u кj кj kj I 5 Ф I 5а I 5 ; u кj кj kj I 2 Ф I 2а I 2 ; u кj кj kj I 4 Ф I 4а I 4 ; u кj кj kj I 6 Ф I 6а I 6 . u кj кj kj (3) В результате получаем: uкI1 ФкI11а I1 ФкI12а I 2 ФкI13а I 3 ФкI14а I 4 ФкI15а I 5 ФкI16а I 6 ; k1 k1 k1 k1 k1 k1 uкI 2 ФкI12а I1 ФкI 22а I 2 ФкI 23а I 3 ФкI 24а I 4 ФкI 25а I 5 ФкI 26а I 6 ; k2 k2 k2 k2 k2 k2 (4) uкI 3 ФкI13а I1 ФкI 32а I 2 ФкI 33а I 3 ФкI 34а I 4 ФкI 35а I 5 ФкI 36а I 6 . k3 k3 k3 k3 k3 k3 В матричном виде эти соотношения имеют следующий вид: u I Ф I 0 0 аkI1 к1 к1 I l uI u I 0 Ф I 0 к к2 аk 2 к2 I 0 ФкI 3 а I uк3 0 k 3 или l u I l Ф I l а I , к к k (5) I – матрица аппроксимирующих функций в где l Фк k блоке для тела I при нагружении пары соответствующих вершин тела III и тела I; l аkI – матрица коэффициентов в k блоке для тела I для всех нагрузок, полученных при решении системы уравнений (2). Аналогично получаем матричные уравнения для перемещений любой точки для тел II и III: цилиндрической оболочки и подкрепляющей окантовки: l u II l Ф II l а II к к k и l u III l Ф III l а III . к к k (6) Для окантовки новые аппроксимирующие функции не были введены, а перемещения ее выражались через перемещения цилиндрической оболочки (тела II): l Ф III l Ф II к к и l а kIII l а kII . z H В результате перемещение любой точки k блока от нагружения пары соответствующих вершин равно l uI l ФI к к l u l u II 0 к к III 0 l uк 0 l Ф II к 0 l а I k l II 0 а k l Ф III l III к а k 0 l u l Ф l а . к к k или (7) Из соотношения (2) коэффициенты равны: (8) После преобразований получаем l а ni М ni kj kj 1 N ni Pi , kj k P1 k 1 М n N n P 2 k k l aI k к 1 3 l a l a II М n N n Pk k к к k 4 l III Pk aк 1 М n N n 5 k Pk k 6 P k или 1 l а М N l P , k k k к (9) 1 М I N I k k 1 1 где М k N k М kII N kII и III 1 III М k N k Т l P P1 k к P2 k P3 k P4 k P5 k P 6 . k Перемещение любой точки k блока можно выразить через нагрузку, приложенную в соответствующей паре вершин: l u l Ф М к к k 1 Nk l Pк . (10) Можно рассмотреть деформированное состояние данного блока под действием нагрузки во всех вершинах шестиугольной пластины. Литература: 1. Амосов А.А. Техническая теория тонких упругих оболочек. [Текст]: Монография/ Амосов А.А. – М.:АСВ, 2009, – 332 с. 2. Филин А.П. Элементы теории оболочек[Текст]: Монография/ Филин А.П..– Л.:Стройиздат, 1975, – 256 с. 3. Огибалов П.М., Колтунов М.Л. Оболочки и пластины[Текст]: Монография/ Огибалов П.М., Колтунов М.Л.–М.:МГУ, 1969, – 696 с. 4. Calladine C.R. Theory of shell structures.[Text]: Monograph/ Calladine C.R. – N.Y.: Cambridge University Press, 1989, –788 p. 5. Zingoni A. Shell structures in civil and mechanical engineering.[Text]: Monograph/ Zingoni A. – N.Y.: Thomas Telford Publishing, 1997, –351 p. 6. Маяцкая И.А.,Краснобаев И.А.,Икуру Годфрей Аарон Прочностной расчет блока составной конструкции из шестиугольной пластины, круговой цилиндрической оболочки и отбортовки. [Электронный ресурс]// «Инженерный вестник Дона», 2013 №2. – Режим доступа: http://ivdon.ru/magazine/archive/n2y2013/1667 (доступ свободный) – Загл. с экрана. – Яз. рус. 7. Маяцкая И.А.,Краснобаев И.А.,Икуру Годфрей Аарон Определение потенциальной энергии шестиугольной отбортовки блока составной конструкции, состоящей из основания в форме шестиугольной пластины, жестко связанной с круговой цилиндрической оболочкой. [Электронный ресурс]// «Инженерный вестник Дона», 2013 №2. – Режим доступа: http://ivdon.ru/magazine/archive/n2y2013/1668 (доступ свободный) – Загл. с экрана. – Яз. рус. 8. Краснобаев И.А.,Маяцкая И.А., Икуру Годфрей Аарон Энергия деформации составной конструкции, состоящей из шестиугольной пластины и круговой цилиндрической оболочки. [Электронный ресурс]// «Науковедение», 2013 №3(16). – Режим доступа: http://www.naukovedenie.ru. /10ТРГСУ313 (доступ свободный) – Загл. с экрана. – Яз. рус. 9. Краснобаев И.А., Маяцкая И.А., Икуру Годфрей Аарон Нагружение блока составной конструкции из шестиугольной пластины и круговой цилиндрической оболочки. [Электронный ресурс]// «Науковедение», 2013 №3(16). – Режим доступа: http://www.naukovedenie.ru./11ТРГСУ313 (доступ свободный) – Загл. с экрана. – Яз. рус. 10. Тимошенко С.П., Войновский-Кригер С. Пластинки и оболочки. [Текст]: Монография/ Тимошенко С.П., Войновский-Кригер С. –М.:Наука, 1966, – 636 с.



