Образец по экономике №1

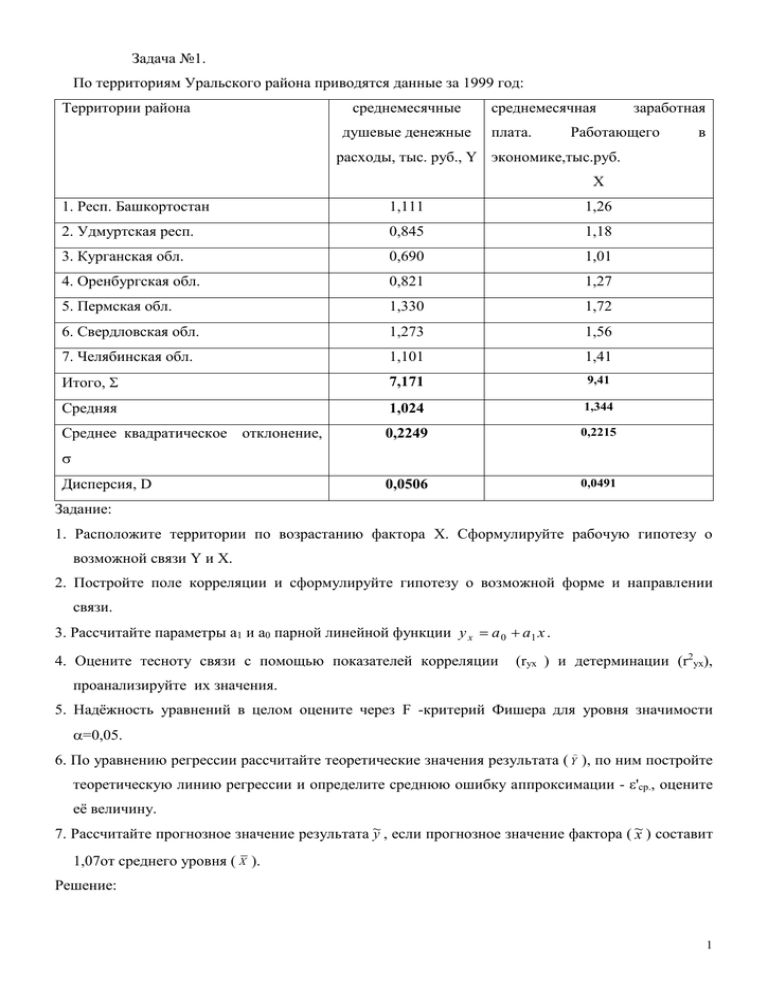
Задача №1.
По территориям Уральского района приводятся данные за 1999 год:
Территории района
среднемесячные
душевые денежные
среднемесячная
плата.
заработная
Работающего
в
расходы, тыс. руб., Y экономике,тыс.руб.
Х
1. Респ. Башкортостан
1,111
1,26
2. Удмуртская респ.
0,845
1,18
3. Курганская обл.
0,690
1,01
4. Оренбургская обл.
0,821
1,27
5. Пермская обл.
1,330
1,72
6. Свердловская обл.
1,273
1,56
7. Челябинская обл.
1,101
1,41
Итого, 
7,171
9,41
Средняя
1,024
1,344
Среднее квадратическое отклонение,
0,2249
0,2215
0,0506
0,0491

Дисперсия, D
Задание:
1. Расположите территории по возрастанию фактора X. Сформулируйте рабочую гипотезу о
возможной связи Y и X.
2. Постройте поле корреляции и сформулируйте гипотезу о возможной форме и направлении
связи.
3. Рассчитайте параметры а1 и а0 парной линейной функции y x  a 0  a1 x .
4. Оцените тесноту связи с помощью показателей корреляции
(ryx ) и детерминации (r2yx),
проанализируйте их значения.
5. Надёжность уравнений в целом оцените через F -критерий Фишера для уровня значимости
=0,05.

6. По уравнению регрессии рассчитайте теоретические значения результата ( Y ), по ним постройте
теоретическую линию регрессии и определите среднюю ошибку аппроксимации - ε'ср., оцените
её величину.
7. Рассчитайте прогнозное значение результата ~y , если прогнозное значение фактора ( ~
x ) составит
1,07от среднего уровня ( X ).
Решение:
1
1.Для построения графика расположим территории по возрастанию значений фактора X i . См.
табл.1.
Таблица 1
Исходные данные
Территории федерального округа
среднемесячная
заработная плата.
работающего в
среднемесячные
душевые
денежные расходы, тыс. руб.,
Y
экономике, тыс.руб.
Х
Курганская обл.
1,01
0,69
Удмуртская Респ.
1,18
0,845
Респ. Башкортостан
1,26
1,111
Оренбургская обл.
1,27
0,821
Челябинская обл.
1,41
1,101
Свердловская обл.
1,56
1,273
Итого, 
9,41
7,171
Средняя
1,344
1,024
Среднее квадратическое отклонение, 
0,2215
0,2249
Дисперсия, D
0,0491
0,0506
1,4
1,3
1,2
Y
1,1
1
0,9
0,8
0,7
0,6
0,5
1
1,1
1,2
1,3
1,4
1,5
1,6
1,7
1,8
X
Рис.1. Корреляционное поле
2. На основании корреляционного поля можно предположить, что связь между исследуемыми
факторами прямая и линейная, Будем искать уравнение прямой: Y  a 0  a1 * X , отражающей
линейную форму зависимости результата Y от фактора X.
2
3.Расчёт неизвестных параметров уравнения выполним методом наименьших квадратов (МНК),
построив систему нормальных уравнений и решая её, относительно неизвестных а 0 и а1. Для
расчёта используем значения определителей второго порядка Δ, Δа0 и Δа1. Расчётные
процедуры представим в разработочной таблице, в которую, кроме значений Y и X, войдут X2,
X*Y, а также их итоговые значения, средние, сигмы и дисперсии для Y и X. См. табл.3.
Таблица 2
Расчётная таблица
№
X
1
1,26
1,111
2
1,18
0,845
3
1,01
0,69
4
1,27
0,821
5
1,72
1,33
6
1,56
1,273
7
1,41
1,101
9,41
7,171
Итого
Средняя
X2
Yфакт .
1,3443
Y *X
Y расч.
'
1,59
1,40
0,945
0,150
1,39
1,00
0,870
0,029
1,02
0,70
0,710
0,030
1,61
1,04
0,954
0,162
2,96
2,29
1,376
0,035
2,43
1,99
1,226
0,037
1,99
1,55
1,086
0,014
12,993
9,962
7,168
0,456
1,0244
Сигма
—
—
Дисперсия, D
—
—
3.Расчёт определителя системы выполним по формуле:
  n * ( X 2 )   X *  X  7*12,993-9,41*9,41=2,4029 ;
Расчёт определителя свободного члена уравнения выполним по формуле:
a0  Y * ( X 2 )  (Y * X ) *  X  7,171*12,993-9,962*9,41 = -0,5696
Расчёт определителя коэффициента регрессии выполним по формуле:
a1  n * (Y * X )  Y *  X  7*9,962-9,41*7,171 = 2,2549.
Расчёт параметров уравнения регрессии даёт следующие результаты:
a0 
a 0  0,5696

 0.237 ;

2,4029
a1 
a1 2,2549

 0,938 .

2,4029
В конечном счёте, получаем теоретическое уравнение регрессии следующего вида:

Yx  0,938 * X  0.237
В уравнении коэффициент регрессии а1 = 0,938 означает, что при увеличении зарплаты на 1
тыс. руб. (от своей средней) денежные расходы вырастут на 0,938 тыс. руб. (от своей средней).
3
Свободный член уравнения а0 =-0,237 оценивает влияние прочих факторов, оказывающих
воздействие на рост денежных расходов.
4.Для оценки тесноты связи рассчитаем линейный коэффициент парной корреляции и
детерминации.:
rYX  a1 *
X
0,2215
 0,938 *
 0,924
Y
0,2249
rYX2  0,854
Коэффициент корреляции, равный 0,924 показывает, что выявлена весьма тесная зависимость
между денежными доходами и денежными расходами. Коэффициент детерминации, равный
0,54 устанавливает, что вариация денежных расходов на 85,4% из 100% предопределена
вариацией заработной платы; роль прочих факторов, влияющих на денежные расходы,
определяется в 14,6%.
5.Для оценки статистической надёжности выявленной зависимости
рассчитаем фактическое
значение F-критерия Фишера – Fфактич. и сравним его с табличным значением – Fтабл.
Fфакт . 
rYX2
0.854
* (n  2) 
* (7  2)  29,2 ;
2
1  0,854
1  rYX
n - число изучаемых объектов. Сравним
полученный результат с табличным значением критерия: Fтабл.  6,61 при степенях свободы
d.f.1=k=1 и d.f.2=n-k-1=7-1-1=5 и уровне значимости α=0,05.
В силу того, что Fфакт .  29,2  Fтабл.  6,61 , нулевую гипотезу о статистической незначимости
выявленной зависимости денежных расходов и средней заработной платы можно отклонить c
вероятностью допустить ошибку значительно меньшей, чем традиционные 5%.
6.Определим теоретические значения результата Yтеор. Для этого в полученное уравнение
последовательно подставим фактические значения фактора X и выполним расчёт.
По парам значений Yтеор. и Xфакт. строится теоретическая линия регрессии, которая пересечётся
с эмпирической регрессией в нескольких точках.
4
среднемесячные расходы. тыс. руб.
1,5
y = 0,938x - 0,237
1,4
1,3
1,2
1,1
1
0,9
0,8
0,7
0,6
0,5
1
1,1
1,2
1,3
1,4
1,5
1,6
1,7
1,8
средняя месячная заработная плата. тыс. руб.
График 1
9.Оценку качества модели дадим с помощью скорректированной средней ошибки аппроксимации:

Yфакт .  Y
1
'  *
*100%  0,456 / 7  6,51% .
n
Y
В нашем случае, скорректированная ошибка аппроксимации составляет 6,51%. Она указывает
на хорошее качество построенной линейной модели и позволяет её использование для
выполнения точных прогнозных расчётов.
~
10. X  Xпрогнозн.= 1,344*1,07=1,438, тогда
прогнозное
значение
~
равно: Y  Yпрогнозн.
=0,938*1,438-0.237=1,112 ( руб.).
5
Задача № 2.
Производится анализ значений социально-экономических показателей по территориям
Волго-Вятского, Черноземного и Поволжского районов РФ за 1999 год:
территории
валовой
объем
инвестиции
региональный
промышленной основной
в доля занятых в
экономике
от
продукт, млрд. продукции,
капитал, млрд. численности
руб.
млрд. руб.
руб.
населения, %.
Y
X1
X2
X3
1
Респ. Марий Эл
6,6
6,8
1,4
41,4
2
Респ. Мордовия
9,3
10,3
2,1
42,3
3
Чувашская респ.
12,1
14,3
3,3
40,8
4
Кировская обл.
16,9
23,0
3,5
42,9
5
Нижегородская
52,7
73,2
12,5
44,9
19,6
30,2
7,2
40,6
23,9
23,8
5,5
40,3
обл.*
6
Белгородская
обл.
7
Воронежская
обл.
8
Курская обл.
16,8
19,8
4,4
43,1
9
Липецкая обл.
17,0
39,4
3,7
41,5
10
Тамбовская обл.
10,5
9,1
1,9
37,5
11
Респ. Калмыкия
1,7
0,9
0,5
37,1
12
Респ. Татарстан*
67,7
100,5
19,8
42,2
13
Астраханская
10,8
10,6
5,4
39,2
30,9
41,3
6,1
40,4
обл.
14
Волгоградская
обл.
15
Пензенская обл.
11,1
13,4
2,6
41,4
16
Самарская обл.*
72,7
108,1
13,4
43,8
17
Саратовская обл.
28,7
30,4
7,3
43,0
18
Ульяновская обл. 16,5
20,7
2,7
40,6
Итого
232,4
294
57,6
612,1
Средняя
15,49
19,6
3,84
40,81
Среднее
7,710
11,49
2,017
1,744
6
квадратическое
отклонение
Дисперсия
59,45
132
4,069
3,042
Требуется изучить влияние указанных факторов на стоимость валового регионального
продукта.
При обработке исходных данных получены следующие значения:
А) - линейных коэффициентов парной корреляции
N=15.
Y
Y
X1
X2
X3
1
X1
X2
X3
0,874
1,000
0,837
0,721
1,000
0,409
0,416
0,329
1,000
Задание:
1.
По
значениям
линейных
коэффициентов
парной
и
частной
корреляции
выберите
неколлинеарные факторы и рассчитайте для них коэффициенты частной корреляции.
Произведите
окончательный
отбор
информативных
факторов
во
множественную
регрессионную модель.
2. Выполните расчёт бета коэффициентов () и постройте с их помощью уравнение
множественной регрессии в стандартизованном масштабе. Проанализируйте с помощью бета
коэффициентов () силу связи каждого фактора с результатом и выявите сильно и слабо
влияющие факторы.
3. По значениям -коэффициентов рассчитайте параметры уравнения в естественной форме (a1, a2
и a0). Проанализируйте их значения. Сравнительную оценку силы связи факторов дайте с
помощью общих (средних) коэффициентов эластичности - Э yx .
4. Оцените тесноту множественной связи с помощью R и R2, а статистическую значимость
уравнения и тесноту выявленной связи - через F -критерий Фишера (для уровня значимости
=0,05).
5. Рассчитайте прогнозное значение результата, предполагая, что прогнозные значения факторов
составят 102.8 процента от их среднего уровня.
6. Основные выводы оформите аналитической запиской.
7
Решение.
1. Представленные в условии задачи значения линейных коэффициентов парной корреляции
позволяют установить, что валовой региональный продукт -Y более тесно связан с объемом
промышленной продукции- x1 ( ryx1  0,874 ) и инвестициями – x 2 ( ryx2  0,837 ); наименее тесно
результат Y связан с долей занятых в экономике – x3 (ryx3=0.409). Чтобы проверить, какой
фактор менее информативен, выполним расчет серии коэффициентов частной корреляции.
Расчёты частных коэффициентов корреляции выполним по следующим формулам:
r
r
yx1*x3
yx3 *x1

r  r *r
yx1 yx3 x1 x3

r  r *r
yx3 yx1 x1 x3
(1 ryx2 )*(1 rx2 x )
3
1 3
(1 ryx2 )*(1 r 2
1
x1x3
r
 r *r
x1 x3 yx1 yx3

)
r

x1 x3 * y
(1 ryx2 )*(1 ryx2 )
1


0,874  0,409 * 0.416
(1  0,409 2 ) * (1  0.416 2 )
0,409  0,874 * 0,416
(1  0,874 2 ) * (1  0,416 2 )
0,416  0,874 * 0,409
(1  0,874 2 ) * (1  0,409 2 )
 0,848
 0,103
 0,132
3
.
Расчёт аналогичных показателей по следующей паре факторов : x 2 и x3
r
yx2 *x3

r  r *r
yx2 yx3 x2 x3
(1 r 2
yx3
)*(1 rx2 x
2 3

)
0,837  0,409 * 0,329
(1  0,409 2 ) * (1  (0.329 2 )
 0.815
8
r

yx3 *x2
r  r *r
yx3 yx2 x2 x3
(1 ryx2
)*(1 rx2 x
2
2 3
r
 r *r
x2 x3 yx2 yx3
r

x2 x3 * y
(1 ryx2 )*(1 ryx2 )
2

)

0,4237  0.8653 * 0,0179
(1  0,8653 2 ) * (1  (0.0179 2 )
0.329  0,837 * 0,409
(1  0,837 2 ) * (1  0,409 2 )
 0.258
114  0,027
3
Таким образом, первая из рассмотренных пар факторных признаков (X1 и X3) в большей мере
отвечает требованиям, предъявляемым
МНК к исходным, т..к. между ними более слабая
межфакторная связь, поэтому будем использовать X1 и X2 в качестве информативных факторов
уравнения множественной регрессии.
2. При построении двухфакторной регрессионной модели Y  a0  a1 * x1  a2 * x2 воспользуемся
для упрощения расчётов методом стандартизованных переменных. В этом случае, исходное
уравнение
приобретает
вид:
t y   yx *t x   yx *t x
1
1
2
.
Выполним
расчёт
-
2
коэффициентов, используя значения известных по условию линейных коэффициентов парной
корреляции.
 yx 
1
 yx 
2
ryx  ryx *rx
1
x
2
1 2  0,874  0.837 * 0,721  0.563 ;
1  0,7212
1 rx2 x2
1
ryx  ryx *rx
2
x
1
1 2  0.837  0,874 * 0.721  0.431 ;
1  0,7212
1 rx2 x
1 2
В результате получено уравнение в стандартизованном масштабе:

t  0.563 * t  0.431 * t
y
x
x2
1
Параметры данного уравнения представляют собой относительные оценки силы влияния
каждого из факторов на результат. При увеличении объема промышленной продукции на
сигму -  x1 (от своей средней) валовой региональный продукт увеличится на 0,563 своей сигмы
(  y ); с увеличением инвестиций на  x 2 результат увеличится на 0,431  y .Сравнивая -
9
коэффициенты, определяем, какой из признаков влияет на результат сильнее, а какой – слабее.
В данном случае, увеличение валового регионального продукта происходит, прежде всего, под
влиянием объема промышленной продукции и в меньшей степени – в результате инвестиций.
3. Используя значения -коэффициентов, можно рассчитать параметры уравнения в естественной
форме:
a1   yx *
1
y
 x1
 0.563 *
7,710
 0,378;
11,49
a2   yx *
2
y
 x2
 0.431 *
7,71
 1,647;
2,017
a0  y  a1 * x1  a2 * x2  15,49  0,378 *19,6  1,647 * 3,84  1,757 .

В конечном счёте, имеем уравнение: Y
 1,757  0,378 * x  1,647 * x . По значениям
x x2
1
2
1
коэффициентов регрессии можно судить о том, на какую абсолютную величину изменяется
результат при изменении каждого фактора на единицу (от своей средней).
С увеличением инвестиций
в основной капитал
валовой региональный продукт
увеличивается на 1,647 млрд. руб., с увеличением объема промышленной продукции валовой
региональный продукт увеличится на 0,378 млрд. руб.
Для сравнительной оценки силы связи выполним расчёт средних коэффициентов эластичности.
x
x
19,6
3,84
Э yx  a * 1  0,378 *
 0,478 ; Э yx 2  a 2 * 2  1,647 *
 0.408 .
1 y
1
15,49
15,49
y
Расчёт показывает, что влияние инвестиций оказалось более сильным по сравнению с объемом
продукции. Различия в силе влияния весьма незначительны
5. Тесноту выявленной зависимости валового регионального продукта от инвестиций 2000 года и
объема промышленной продукции
оценивает множественный коэффициент корреляции и
детерминации. Расчёт коэффициента корреляции выполним, используя известные значения
линейных коэффициентов парной корреляции и β – коэффициентов: R yx 
j
 ryx
j
*  yx j . В
нашем случае 2-х факторной зависимости расчёт строится следующим образом:
R
yx x3
1
 r
yx
1
*
yx
1
r
yx
*
2
yx
 0,923 .
2
R2
 0,852.
yx1 x3
10
Как показали расчёты, установлена весьма тесная зависимость валового регионального
продукта года от инвестиций и объема промышленной продукции. Это означает, что 85,2%
вариации валового продукта определены вариацией данных факторов.
7. Оценка статистической значимости или надёжности установленной формы зависимости, её
параметров, оценок её силы и тесноты является важным этапом анализа результатов. Для
выполнения оценки формулируется нулевая гипотеза, которая рассматривает предположение о
случайной природе полученных результатов.
Для проверки выдвинутой нулевой гипотезы используется F-критерия Фишера. Его
фактическое значение определяется, исходя из соотношения факторной и остаточной
дисперсий и их степеней свободы: d.f.1=k и d.f.2=n-k-1; где: n –число изучаемых единиц; k –
число ограничений, которые накладываются на исходные данные при расчёте данного
показателя. Здесь k равно числу факторов уравнения, то есть k=2.
R2
yx j
k
.
F

:
факт.
2
n

k

1
1 R
yx j
В нашем случае, когда рассматривается зависимость результата от двух факторов, расчёт
выглядит следующим образом:
R2
yx x
k
0,852
2
1 2 :
F


:
 34,5 .
факт.
2
n

k

1
1

0
,
852
15

2

1
1 R
yx x
1 2
Для принятия обоснованного решения Fфактич. сравнивается с Fтабличн., которое формируется
случайно и зависит
степеней свободы факторной (d.f.1
= k) и остаточной (d.f.2 = n-k-1)
дисперсий, а также от уровня значимости α=0,1. В нашем примере, где d.f.1=k= 2 и d.f.2=n-k-1 =
15-2-1=12 при α=0,01 Fтабл = 6,93. В силу того, что Fфактич =34,5> Fтабл. = 6,93, то можно c
высокой степенью надежности отклонить нулевую гипотезу, что проверяемые параметры
множественной регрессионной модели случайны, что коэффициенты уравнения и показатели
тесноты связи являются случайными величинами.
5.
~
x1  x1 *1,028  19,6 *1,028  20,15 .
~
x2  x2 *1,028  3,84 *1,028  3,95 .
После подстановки в уравнение получаем следующий результат:
~
y ~ ~  1,757  0,378 * 20,15  1,647 * 3,95  15,88 (млрд. руб.)
x x
1; 2
11
Если инвестиции возрастут до 3,95 млрд. руб., а объем продукции составят 20,15 млрд. руб.,
тогда следует ожидать, что валовой региональный продукт составит 15,88 млрд. руб.,(102,52%),
то есть увеличатся на 2,52% от своего среднего уровня.
Задача № 3.
Предлагается изучить взаимосвязи социально-экономических показателей региона за период.
Y1  среднемесячная начисленная заработная плата, тыс. руб.;
Y2
Среднемесячный душевой доход тыс. руб.;
Y3  число совершенных преступлений в среднем на 100 тыс. жителей;
X1  индекс потребительских цен на товары и услуги;
X 2  индекс физического объема промышленного производства;
X3 – численность безработных в процентах от экономически активного населения, %
X4 – среднемесячный прожиточный минимум 1-ого трудоспособного, тыс. руб.
X5- процент лиц с высшим образованием среди безработных
X  среднемесячный размер назначенной пенсии, тыс. руб.
6
Приводится система рабочих гипотез, справедливость которые необходимо проверить:
Y1  f (Y2 , X 1 , X 2 , X 3 , X 4 );

Y2  f (Y1 , Y3 , X 1 , X 4 , X 5 , X 6 );
Y  f (Y , Y , X , X , X , X , X ).
1
2
1
3
4
5
6
 3
Задание:
1.На основе рабочих гипотез постройте систему структурных уравнений и проведите их
идентификацию;
2.Укажите, при каких условиях может быть найдено решение каждого из уравнений и системы в
целом. Дайте обоснование возможных вариантов подобных решений и аргументируйте выбор
оптимального варианта рабочих гипотез;
3.Опишите методы, с помощью которых может быть найдено решение уравнений (косвенный
МНК, двухшаговый МНК).
Решение
В состав структурных уравнений входят: а) эндогенные переменные (Yj), значения которых
формируется в условиях данной системы признаков и их взаимозависимостей и б) экзогенные
переменные (xm), значения которых формируются вне данной системы признаков и условий, но
12
сами экзогенные переменные участвуют во взаимосвязях данной системы и оказывают влияние
на эндогенные переменные. Коэффициенты при эндогенных переменных обозначаются через
a m ,i , коэффициенты при экзогенных переменных обозначаются через b j ,i , где i-число
изучаемых объектов; m –число экзогенных переменных, которые обычно обозначают через x;
j - число эндогенных переменных, обычно обозначаемых через Y. Таким образом, в каждом
уравнении системы каждый коэффициент при переменной имеет двойную индексацию: 1) номер эндогенной переменной, расположенной в левой части уравнения и выступающей в
качестве результата; 2) – номер переменной, находящейся в правой части уравнения и
выступающей в качестве фактора.
В нашей задаче система уравнений для описания выдвигаемых рабочих гипотез будет иметь
следующий вид:
Y1  a12 * Y2  b11 * x1  b12 * x2  b13 x3  b14 x4

Y2  a 21 * Y1  a 22 * Y3  b21 * x1  b24 * x4  b25 * x5  b26 * x6
Y  a * Y  a * Y  b * x  b * x  b * x  b * x  b * x
31
1
32
2
31
1
33
3
34
4
35
5
36
6
 3
2.Выполним идентификацию каждого структурного уравнения и всей системы для ответа на
вопрос – имеют ли решения каждое из уравнений и система в целом. Воспользуемся счётным
правилом, по которому в каждом уравнении системы необходимо сравнить HY - число
эндогенных переменных в данном уравнении и Dx - число отсутствующих в уравнении
экзогенных переменных из общего для всей системы их перечня. Для удобства анализа
представим результаты в таблице.
Результаты идентификации структурных уравнений и всей системы.
Номер
Число
Число
уравне
эндогенных
переменных из общего их параметров
ния
переменных
1
в списка,
экзогенных Сравнение
отсутствующих
уравнении, HY
уравнении, Dx
2
2
в HY и Dx + 1
2 <2+1
Решение
об
идентификации
уравнения
сверх
идентифициров
ано
2
3
2
3 < 2+1
точно
идентифициров
ано
3
3
1
3 < 1+1
Сверх
идентифициров
ано
13
Вся система уравнений в целом
идентифициров
ана
4. Для поиска решений сверхидентифицированной системы уравнений применяются: а) косвенный
метод наименьших квадратов (КМНК) для решения точно идентифицированных уравнений и б)
двухшаговый МНК (ДМНК) для поиска решений сверхидентифицированных уравнений.
Задача № 5.
По 18 территориям Центрального федерального округа России имеются данные о следующих
показателях за 2000 год:
Y1 – розничный товарооборот, млрд. руб.
Y2 – сумма доходов населения за год, млрд.руб.
X1 – численность занятых в экономике, млн.чел.
X2 – основные фонды в экономике, млрд. руб.
X3- объем промышленной продукции, млрд. руб.
Для изучения связи социально-экономических показателей предполагается провести
проверку следующих рабочих гипотез:
Y  f (Y , X , X );
 1
2 1 2

Y  f (Y , X 2 , X ).
1
3
 2
Для их проверки выполнена обработка фактических данных и получена следующая система
приведённых уравнений:

2
 13.9.
Y  0.738  8.15 X  0.051X  0.933 X ; R  0,791; F
1
2
3
фактический
 1

Y  0.046  0.968 X  0.0074 X  0.0082 X ; R 2  0,897; F
 31.9.
 2
1
2
3
фактический

Задание:
1.Постройте систему структурных уравнений и проведите её идентификацию;
2.Проанализируйте результаты решения приведённых уравнений;
3.Используя результаты построения приведённых уравнений, рассчитайте параметры структурных
уравнений (косвенный МНК); проанализируйте результаты;
4.Укажите, каким образом можно применить полученные результаты для прогнозирования
эндогенных переменных Y1 и Y2 .
14
Решение
1. Построение системы структурных уравнений выполняется в соответствии с рабочими
гипотезами:
Y1  a12 * Y2  b11 * x1  b12 * x 2

Y2  a 21 * Y1  b22 * x 2  b23 * x 3
2. В соответствии со счётным правилом оба уравнения и система в целом являются точно
идентифицированными и это означает, что они имеют единственное решение, которое может
быть получено косвенным МНК (КМНК).
Номер
Число
Число экзогенных перемен- Сравнение
Решение
уравне
эндогенных
ных из общего их списка, параметров
идентификации
ния
переменных
в отсутствующих в уравнении, HY и Dx + 1
1
уравнении, HY
Dx
2
1
2 = 1+1
об
уравнения
точно идентифицировано
2
2
1
2 = 1+1
точно
идентифицирова
но
Система уравнений в целом
точно
идентифицирова
на
3. Процедура КМНК состоит в том, чтобы путём преобразования результатов решения
приведённых уравнений получить искомые структурные уравнения. Используемый приём
подстановок обеспечивает получение точных результатов только в том случае, если
выполняемые преобразования точны и безошибочны. Чтобы получить первое структурное
уравнение из первого приведённого необходимо отсутствующий в структурном уравнении
признак x3 выразить через Y2, используя результаты второго приведённого уравнения. То есть:
Y  0.046  0,968 * x1  0.0074 * x
2
x3  2
0.0082
После подстановки значения x1 в первое приведённое уравнение и преобразования подобных
членов, получаем следующий результат:
Y  0.046  0.968 * x  0.0074 * x

1
2 
Y1  0.738  8.15 * x1  0.051 * x 2  0.933 *  2

0.0082


15
 4.495  113.78 * Y  101.99 * x  0.791 * x .
2
1
2
Анализ показывает, что розничный товарооборот находится в прямой зависимости от суммы
доходов населения и от численности занятых в экономике и от основных фондов. Указанные
переменные объясняют 79,1% вариации результата, а характеристики установленной
зависимости являются статистически значимыми и надёжными, так как
Fфактич.  13.9  Fтабл.  3.59 для d . f .1  3; d . f .2  15  3  1  11;  0,05 .
Следовательно, есть основания для отклонения нулевой гипотезы о случайной природе
выявленной зависимости.
Аналогично выполняем преобразования для определения параметров второго структурного
уравнения. Выразим отсутствующий в уравнении x1 через Y1, используя результаты
построения первого приведённого уравнения. То есть:
Y  0.738  0,051 * x 2  0.933 * x
3.
x1  1
8.15
После подстановки значения x1 во второе приведённое уравнение и преобразования подобных
членов, получаем следующий результат:
 Y  0.738  0,051 * x 2  0.933 * x3  
Y  0.046  0.0074 * x 0.0082 * x 3  0.968 *  1

2
2
8.15


 0.418  0.009 * Y1  0,0013 * x2  0.0021 * x3 .
Уравнение описывает линейную зависимость суммы доходов населения за год от розничного
товарооборота, основных фондов в экономике, объема промышленной продукции.
Данный перечень переменных объясняет 89,7% вариации суммы доходов а соотношение
F
 31.9  F
 3.59 позволяет отклонить нулевую гипотезу о случайной природе
фактич.
табл.
выявленной зависимости.
~
~
4. Для выполнения прогнозных расчётов Y1 и Y 2 наиболее простым является вариант, по которому
x i , j ) подставляются в приведённые уравнения.
прогнозные значения экзогенных переменных ( ~
Точность и надёжность прогнозов в этом случае зависит от качества приведённых моделей и от
того, как сильно отличаются прогнозные значения экзогенных переменных от их средних
значений.
16
17