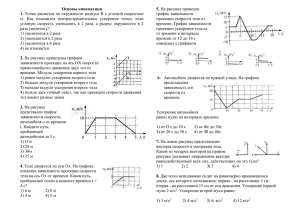
Указания к задачам 8 вариант

Вариант 8.
1.19. Начало системы координат выберите в точке, из которой тело
начало движение. Ось OX направьте горизонтально в сторону движения, а
ось OY - вертикально вверх. Начало отсчета времени соответствует началу
движения тела. В случае свободного падения a  g , где a - ускорения мяча,
g - ускорение свободного падения. При таком выборе системы отсчета
g  OX . Составьте зависимость координаты Y от времени. По условию
задачи, координата Y принимает одинаковые значения в известные, но
разные моменты времени. Это дает возможность составить уравнение для
определения значения проекции начальной скорости на ось OY и вычислить
модуль начальной скорости. Время подъема до максимальной высоты
определите из условия равенства нулю проекции скорости на ось OY .
Используйте это время для вычисления максимальной высоты по формуле
зависимости координаты Y от времени.
1.40. Нормальное ускорение выразите через скорость тела и радиус его
траектории (1.8). При движении с постоянным тангенциальным ускорением,
скорость тела равна произведению тангенциального ускорения на время.
Составьте соответствующее отношение и получите ответ.
2.19. Систему координат удобно выбрать так, чтобы ось OX была
направлена вдоль наклонной плоскости в сторону движения ящика, а ось OY
– перпендикулярно наклонной плоскости, вверх. Запишите П закон Ньютона
в проекциях на оси координат. Так как тело движется с постоянной
скоростью, то проекции ускорения на эти оси равны нулю. Решите
получившуюся систему уравнений.
2.34. В крайнем положении тело, подвешенное на нити неподвижно,
поэтому его ускорение равно нулю. В положении равновесия тело движется
по дуге окружности, поэтому его ускорение равно нормальному ускорению
(1.8). Запишите П закон Ньютона для каждого случая в проекции на
направление нити маятника. Выразите силы натяжения нити и
сформулируйте ответ на вопрос задачи.
3.19. Средняя мощность двигателя автомобиля равна отношению
работы силы тяги ко времени движения. Для определения силы тяги
выберите систему координат так, чтобы ось OX была направлена вдоль
наклонной плоскости в сторону движения автомобиля, а ось OY –
перпендикулярно наклонной плоскости, вверх. Запишите П закон Ньютона
для автомобиля в проекциях на оси координат. Проекцию ускорения на ось
OX и время движения найдите, используя формулы равноускоренного
движения (1.11, 1.12). Проекция ускорения на ось OY равна нулю.
Мгновенная мощность равна произведению силы тяги на скорость тела в
данный момент времени.
3.45. В соответствии с законом сохранения энергии, энергия упругой
деформации резинового шнура рогатки (2.9) переходит в кинетическую
энергию камня (2.8). Это уравнение позволит вам выразить скорость камня.
Для определения коэффициента упругости резины воспользуйтесь законом
Гука (2.2).
4.19. Выразите вращающийся момент из основного закона динамики
вращательного движения (3.1). Угловое ускорение стержня можно вычислить
по определению, как вторую производную зависимости угла поворота от
времени (1.15, 1.16).
4.44. Кинетическая энергия, катящегося без скольжения диска (3.13),
при подъеме вверх по наклонной плоскости переходит в потенциальную
энергию тела в поле тяжести Земли (En=mgh). Связь угловой скорости
вращения диска и линейной скорости точек на его поверхности определяется
формулой (1.20). Так как диск катится без проскальзывания, то линейная
скорость точек на поверхности диска равна скорости поступательного
движения его центра масс. Используя закон сохранения полной
механической энергии, определите, на какой высоте окажется диск в момент
остановки. Эта высота – противолежащий углу  катет, а путь – гипотенуза
соответствующего прямоугольного треугольника.
5.9. Для ответа на вопрос воспользуйтесь формулой периода малых
колебаний физического маятника (4.6). Момент инерции конструкции равен
сумме моментов инерции шариков относительно оси вращения (3.3) и
стержня относительно оси, проходящей через конец стержня (3.6).
Расстояние от оси до центра масс (центра тяжести) конструкции вычисляется
по определению центра масс (2.5).
5.34. Это время равно 1/4 периода колебаний. Величину периода
колебаний вычислите из уравнения свободных гармонических колебаний
точки (4.2).