Чупрей Д.Р. Формирование исследовательских компетенций при изучении алгебры в 7 классе.

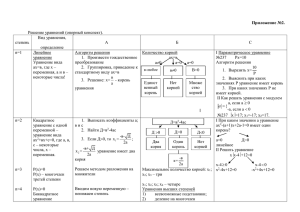
Чупрей Д.Р.
Формирование исследовательских компетенций
при изучении алгебры в 7 классе.
Основная задача учителя в соответствии с требованиями ФГОС –
организовать получение образования через деятельность и в деятельности.
Для этого требуется такая организация образовательной ситуации, при
которой происходит самостоятельное извлечение образовательного
содержания из практического опыта. Главным образовательным звеном в
учебном процессе является самостоятельная познавательная деятельность
ученика, обязательно практическая и продуктивная. Важное место в этой
деятельности занимает формирование исследовательских компетенций как
инструментов адаптации учащихся к жизни после окончания
общеобразовательного учреждения, поскольку в процессе их формирования
развивается способность самостоятельно принимать решение, находить
оптимальные варианты развития ситуаций, генерировать идеи и предлагать
проекты.
Под категорией «исследовательская компетенция» понимается
многокомпонентное образование, эффективность развития которого
происходит за счёт стимулирования познавательной деятельности учащихся,
насыщения учебно-воспитательного процесса исследовательскими формами
работы, использования и необходимого сочетания традиционных и
инновационных форм работы, проблемных и исследовательских методов
обучения.
Чтобы
добиться
результатов
в
процессе
формировании
исследовательских компетенций, педагог учит обучающегося самостоятельно
мыслить, находить пути решения проблемы, прогнозировать результаты и
возможные последствия разных вариантов решений, устанавливать
причинно-следственные связи, оценивать полученные результаты и выявлять
способы совершенствования действий, привлекая для этой цели знания из
разных предметных областей.
Формирование исследовательских компетенций происходит в процессе
учебной
работы.
Под
«учебно-исследовательской
деятельностью»
понимается особый вид деятельности, направленный на получение новых
объективных научных знаний, связанный с поиском заранее неизвестного
решения проблемы.
Задача педагога — создать развивающую среду, в которой задаются
формы и условия, способствующие формированию у учащегося внутренней
мотивации подходить к любой возникающей перед ним проблеме с
исследовательской позиции, научить уверенно действовать в ситуации
неопределённости.
Решение задач с параметрами
позволяет формировать
исследовательские компетенции учащихся в рамках предмета. Практически
каждое задание – это мини-исследование с неопределённым заранее
результатом, поскольку в них наряду с неизвестными фигурируют величины,
численные значения которых хотя и не указаны конкретно, но считаются
известными и заданными на некотором числовом множестве. Параметры,
входящие в условие, существенно влияют на логический и технический ход
решения и форму ответа. Важная часть решения задачи — выяснить, как зависит
ответ от параметра. И это исследование проводится каждый раз заново.
В курсе алгебры 7 класса учащиеся встречаются с параметрами, когда
вводятся понятия
• уравнения первой степени: ах + b = 0 (х - переменная, а и b — параметры,
a≠0);
• прямой пропорциональности: у = кх (х и у - переменные, к - параметр,
к ≠ 0;
• линейной функции: у = кх + b (х и у- переменные, к и b- параметры).
Далее предлагаются разработки занятий по теме «Линейные уравнения с
параметрами», которые можно использовать как
в урочной, так и
внеурочной
деятельности,
например,
при
проведении
занятий
математического кружка или подготовке уроков
для создания
индивидуальной траектории наиболее способным учащимся.
Приложение 1
Конспект занятия
Тема: «Линейные уравнения с параметрами».
Занятие №1.
Цель занятия: ввод определения линейного уравнения с параметром,
создание алгоритма решения линейного уравнения с параметром,
формирование исследовательской компетенции учащихся, их рефлексивных
навыков.
Ход занятия:
I.
Вводная часть.
1. Организационный момент.
2. Устно:
1) Выбрать из предложенных уравнений линейные:
𝑥
1
3
𝑥
а) 5x+3=0; б) 3x=0; в) (x-5)(x+3)=0; г) =8; д)
=8.
Ответ: а), б), г).
2) Определить, при каких значениях a число 5 является корнем
уравнения:
а) ax=7;
б) 2x=3a;
10
Ответ: a=1,4.
Ответ: a= .
3
Основная часть.
1. В тетрадях выполнить упражнение:
Определить, при каких значениях b число 3 является корнем уравнения
(4b+1)x=b-5 и (5+b)x=7+3b.
I вариант
II вариант
II.
(4b+1)x=b-5.
Решение: (4b+1)3=b-5,
12b+3=b-5,
b= Ответ: при b= -
8
11
8
11
.
.
(5+b)x=7+3b.
Решение: (5+b)3=7+3b,
15+3b=7+3b,
0b= - 8.
Ответ: таких значений b нет.
2. Опираясь на определение линейного уравнения, рассмотреть случаи
возможного количества корней.
Определение №1.
Уравнение вида ax=b, где x – переменная, a, b –некоторые числа,
называется линейным уравнением с одной переменной. Повторим, сколько
корней может иметь линейное уравнение.
1) При a ≠ 0, x=
𝑏
𝑎
- единственный корень.
2) При a = 0, b≠0 уравнение корней не имеет.
3) При a = 0, b = 0 уравнение имеет бесконечное множество
корней.
Решить линейное уравнение – это значит найти все его корни или показать,
что корней нет.
Чем же обычное линейное уравнение отличается от линейного уравнения с
параметром?
Определение №2.
Пусть дано равенство с переменными x, a: f(x, a)=0.
Если ставится задача: для каждого действительного значения a решить это
уравнение относительно x, то уравнение f(x, a)=0 называется уравнением с
переменной x и параметром a.
Решить уравнение с параметром a – это значит для каждого значения a
найти значения x, удовлетворяющие этому уравнению.
В качестве объяснения учитель решает уравнение относительно x:
a(a-1)x=(a-1)(a+2).
Решение: 1) При a ≠ 0 и a ≠ 1
x=
(𝑎−1`)(𝑎+2)
𝑎(𝑎−1)
, x=
𝑎+2
𝑎
– один корень.
2) При a=0
0x=-2 корней нет.
3) При a=1
0x=0 бесконечное множество корней.
По разобранному алгоритму совместно с учащимися создаётся алгоритм
решения линейного уравнения с параметрами:
1) Привести исходное уравнение к виду ax=b.
2) Выяснить, при каких значениях параметра коэффициент при х не равен
нулю (один корень).
3) Выяснить, при каких значениях параметра коэффициент при х равен
нулю, а свободный член не равен нулю (корней нет).
4) Выяснить, при каких значениях параметра коэффициент при х и
свободный член равны нулю (бесконечное множество корней).
5) Записать ответ.
3. Решить упражнения.
№1. При каких значениях параметра n уравнение (n2-4)х=n3-2n2- n+2
а) имеет единственный корень;
б) не имеет корней;
в) имеет бесконечное множество корней?
Решение: (n2-4)х=n3-2n2- n+2,
(n-2) (n+2)х= n2(n-2)-(n-2)
(n-2) (n+2)х=(n-2) (n2-1),
(n-2) (n+2)х=(n-2) (n-1) (n+1),
а) при n≠ -2 и n≠ 2
x=
𝑛2 −1
𝑛+2
– один корень
б) при n=-2 корней нет;
в) при n=2 бесконечное множество корней.
Ответ: при n≠ -2 и n≠ 2
x=
𝑛2 −1
𝑛+2
– один корень
при n=-2 корней нет;
при n=2 бесконечное множество корней.
№2.
Составьте уравнение с параметром а такое, чтобы оно имело решение при
любом а (например, х=а, 2х=1-а, (а2+3)х=а).
№3.
Составьте уравнение с параметром n такое, чтобы оно имело бесконечное
множество корней при n= 3 (например, (9- n2)х=3-n, (3- n)х= n2-6n+9).
№4.
Составьте уравнение с параметром а такое, чтобы оно не имело корней при
а=5 (например, (а-5)х=а).
№5.
Какие случаи следует выделить при решении уравнения:
а) nх=7;
б) (b2-4)x=3b +12?
Решение:
Решение:
nх=7
(b2-4)x=3b +12
7
1) при n ≠ 0 х= – один корень;
𝑏
2) при n =0 корней нет.
Ответ: следует выделить случаи
при n ≠ 0 и n =0.
III.
Заключение. Рефлексия.
1) при b≠ ±2 х=
3(𝑏+4)
(𝑏−2)(𝑏+2)
один корень;
2) при b=±2 корней нет.
Ответ: надо выделить случаи
b≠ ±2 и b=±2.
Приложение 2
Конспект занятия
Тема: «Линейные уравнения с параметрами».
Занятие №2.
Цель занятия: закрепление навыков решения линейных уравнений с
параметром, формирование способности действовать в условиях
неопределённости, анализировать имеющиеся данные, осуществлять
рефлексию собственной деятельности.
Ход занятия:
I.
Вводная часть.
1. Организационный момент.
2. Устно:
1) Решить уравнение относительно х:
а) ах=3.
Решение:
3
При а≠0 х= - один корень,
а
При а=0 корней нет.
б) (n-2)х=5.
Решение:
При n≠2 уравнение имеет 1 корень х=
5
,
𝑛−2
При n=2 уравнение корней не имеет.
в) 0х=а.
Решение:
При а=0 уравнение имеет бесконечное множество решений,
при а≠ 0 уравнение корней не имеет.
2) Определить, при каких значениях b число 4 является корнем
уравнения
bх= -8? (При b= -2).
3) Найти ошибку:
2
(а+1)х=а -1,
(а+1)х=(а+1)(а-1),
при а≠1 уравнение имеет 1 корень,
при а=-1 уравнение корней не имеет.
Ошибка: уравнение имеет 1 корень при а≠ −1 и при а=-1 бесконечное
множество корней.
II.
Основная часть.
№1. Вспомнить определение и алгоритм решения линейного уравнения с
параметрами на примере уравнения (а-2)х=10-5х.
Решение: (а-2)х=10-5х,
(а-2)х+-5х=10,
(а+3)х=10,
при а≠-3, х=
10
а+3
– 1 корень,
при а=-3 уравнение корней не имеет.
№2. При каких значениях а имеют общий корень уравнения
а) 8х - 1=0 и 3х+а=0; б) 3х+7=0 и 2х - а=0?
3
14
8
3
Ответ: а) при а=- ; б) при а=-
.
№3. Решить уравнения с параметрами:
а) b2x=b(x+1); б) bx(b+1)=5b-bх; в) (с2-9)х+4=2(х+6)-7х.
Решение:
а) b2x=b(x+1),
b2x- bx= b,
b(b-1)x= b,
при b ≠0, b ≠1, х=
1
𝑏−1
-1 корень,
при b=0 бесконечное множество корней,
при b=1 корней нет;
б) bx(b+1)=5b-bх,
b2x- bх+ bх =5b,
b2x =5b,
5
при b ≠0, х= -1 корень,
𝑏
при b=0 бесконечное множество корней;
в) (с2-9)х+4=2(х+6)-7х,
(с2-9)х+5х=12-4,
(с2-4)х=8,
(с-2)(с+2)х=8,
при с≠2, с≠-2
х=
8
с2 −4
-1корень,
при с=-2 и с=2 корней нет.
3
9
𝑏
𝑏2
№4.При каких значениях b уравнения = 8-х и х-10 =
3
а) = 8-х.
б) х-10 =
𝑏
Решение:
3
𝑏
х-10 =
3
(𝑏2 −9)
𝑏
𝑏2
х( +1)=8;
3+𝑏
𝑏
𝑏2
х;
Решение:
+ х= 8,
х(
9
х не имеют корней?
9
𝑏2
х;
x=10;
)=8.
Ответ:
уравнение
при b=0 и b = - 3.
III.
не
имеет
Ответ:
уравнение не
корней при b=0 и b = ±3.
Заключительная часть. Рефлексия.
имеет
Приложение 3
Конспект занятия
Тема: «Линейные уравнения с параметрами».
Занятие №3.
Цель занятия: закрепление навыков решения линейных уравнений с
параметрами,
формирование
навыков
деятельности
в
условиях
неопределённости, развитие навыков рефлексии собственной деятельности.
Ход занятия:
Вводная часть.
1. Организационный момент.
2. Устно:
1. Решить уравнение относительно х:
а) ах=а,
б) сх=6,
6
а≠ 0, х=1, 1 корень,
с≠0, х= , 1 корень,
с
а=0, х-любое.
с=0, корней нет.
2. При каком значении k уравнение 3х+ ky=15 имеет решение
х=-2, y=7? (При y=3).
3. Придумать линейное уравнение относительно х с параметром а, имеющее
бесконечное множество корней при а=1.
(Например, (а-1)х=(а-1)(а-2)).
II.
Основная часть.
1. Работа по вариантам.
(Два человека за доской, остальные в тетрадях с последующим разбором).
I.
а) При каких значениях а и b прямая y=ax+b проходит через точки
1 вариант
2 вариант
М(1; 5) и N(-5;-3)?
М(-1; 5) и N(1;-3)?
4
11
4
11
Ответ: при а= , b= .
Ответ: при а=- , b= .
3
3
3
3
б) Какие случаи следует выделить при решении уравнения
1 вариант
2 вариант
2
(b -1)х=4b+4?
(с2-9)х=2с+6?
Ответ:1) b≠ ±1;
Ответ:1) с≠ ±3;
2) b=1;
2) с=3;
3) b=-1.
3) с=-3.
2. Решить уравнения:
а) сх(с-2)+9=с(х+с),
с2х-2сх+9=сх+с2,
(с2-3)х=с2-9,
с(с-3)=(с-3)(с+3).
3
Ответ: 1) с≠0 и с≠3 х=с+ , 1 корень;
с
2)с=0 корней нет;
3) с=3 бесконечное множество корней.
б) При каких значениях a и b уравнение
(2х-а)(18х+1)=(6х-1)2 + b имеет не менее трёх различных корней?
Решение:
36х2 +2х-18ах-а=36х2-12х+1+ b,
14х-18ах=а+ b+1,
7
1
а) при а≠ х=а+b+ (7-9а) один корень;
б) при а=
9
7
9
7
2
-корней нет;
в) при а= и а+ b+1=0 -бесконечное множество корней,
9
7
7
9
9
если а= , b=1 .
7
7
Ответ: уравнение имеет не менее трёх корней при а= и b=1 .
9
9
3.Обучающая самостоятельная работа. Проверка осуществляется по
образцу через взаимопроверку.
1 вариант
2 вариант
Решить уравнения относительно х:
а) (а+1)(а-1)х=а+1;
а) (а-2)(а+2)х=а-2;
б) (b2-4)x+5=3(x+3).
б) (с2-3)х+8=4(х+3)+2х.
1
Ответы: а) а≠ ±1 х=
а−1
– 1 корень;
а=-1 беск. мн-во корней;
а=1 корней нет
б) b≠ ±3 х=
16
𝑏2 −9
а) а≠ ±2 х=
1
а+2
– 1 корень;
а=2 беск. мн-во корней;
а=-2 корней нет.
-1 корень,
б) с≠ ±3 х=
b=±3 корней нет.
4
с2 −9
-1 корень,
с=±3 корней нет.
4. Резервное упражнение.
Прямая y=kx+b проходит через точки М(2;-5) и К(0;-2). Написать уравнение
этой прямой.
3
Ответ: y= - x-2.
2
III.
Заключительная часть. Рефлексия.
Приложение 4
Конспект занятия
Тема: «Линейные уравнения с параметрами».
Занятие №4.
Цель занятия: контроль знаний учащихся, формирование навыков
деятельности в условиях неопределённости, развитие навыков рефлексии
собственной деятельности.
Ход занятия:
Мотивация, постановка цели, комментирование текста контрольной
работы.
II.
Выполнение контрольной работы.
Вариант 1
Вариант 2
I.
№1. Решить уравнение относительно х:
а) ах=4;
а) сх=2;
2
б) (с -9)х=с-3;
б) (а2 -25)х=а-5;
в) (с-5)(с+3)х=с2-25;
в) (с+3)(с+7)х=с2-49;
г) (а2-16)х=а3-4а2-а+4.
г) (а2-36)х=а3-6а2-а+6.
№2.
Составьте уравнение с параметром а
такое, чтобы оно имело бесконечное
множество корней при а=2.
№2.
Составьте уравнение с параметром а
такое, чтобы оно имело бесконечное
множество корней при а=4.
№3.
Постройте график уравнения
5х-y=a, если известно, что он проходит
через точку А(-1;-2).
№4.
При каком целом неотрицательном
значении n уравнение (х+n)2-(х-n)2=56
имеет только целые корни?
№3.
Постройте график уравнения
3х-y=a, если известно, что он проходит
через точку В(-1;-1).
№4.
При каком целом неотрицательном
значении n уравнение (х-n)2-(х+n)2=-48
имеет только целые корни?
III.
Заключительная часть. Рефлексия.