Расчет рамы испытывающей динамические
реклама
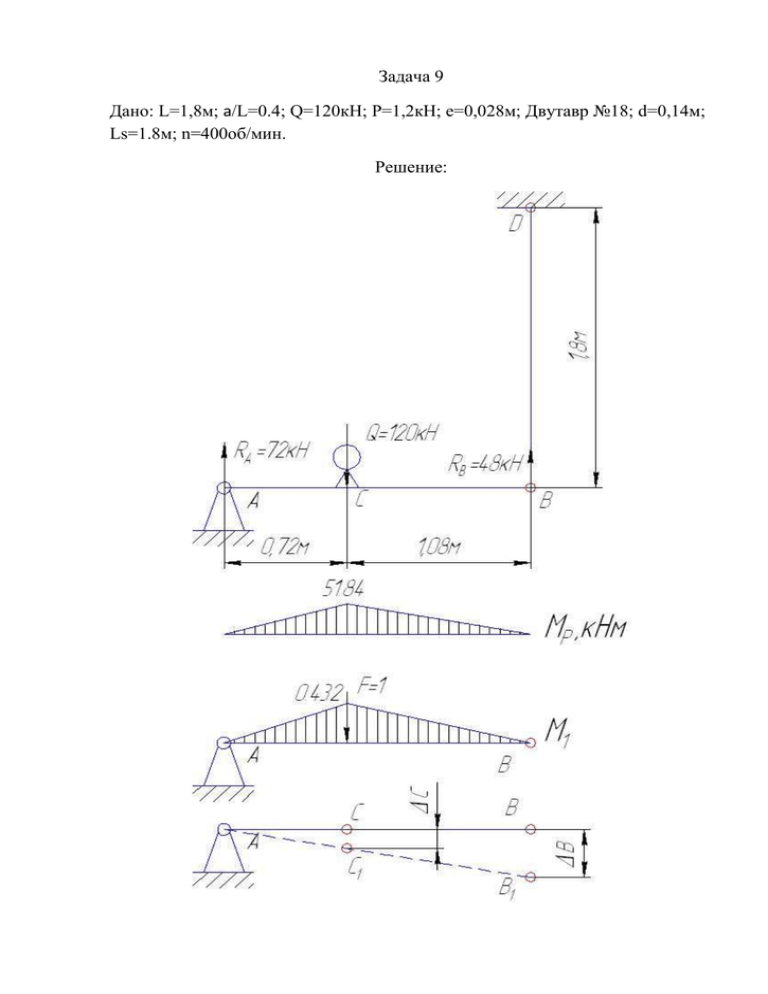
Задача 9 Дано: L=1,8м; а/L=0.4; Q=120кН; Р=1,2кН; е=0,028м; Двутавр №18; d=0,14м; Ls=1.8м; n=400об/мин. Решение: Вычислим реакции опор МА=0 RВ Q 0,72 48кН 1.8 МВ=0 RА Q 0,72 RВ 1.8 0 Q 1.08 RА 1.8 0 Q 1.08 72кН 1.8 Строим эпюру изгибающих моментов. Определим статическое перемещение точки приложения груза (прогиб балки). 0,72 2 0,432 51,84 1,08 2 0,432 51,84 13,436 6 EI EI 6 EI c Двутавр №18 Wx 143см 3 ; J x 1290см 4 Подставим значения: c 13,436 13,436 2604 10 9 м/н 11 8 EI 2 10 1290 2 10 На самом деле, точка В за счет удлинения стержня ВD переместится на величину В =ВВ1 Это удлинение происходит под влиянием опорной реакции в точке В. В 48 LS 4 48 1,8 4 28 10 9 м/н 2 11 2 Ed 2 10 3,14 0,14 Из подобия треугольников C 0,72 В 1110 9 м/н 1,8 Полное вертикальное перемещение точки С будет равно C C c 2615 10 9 м/н Частота свободных колебаний 0 g 9,8 55,88c 1 3 9 Q C 120 10 2615 10 Вертикальная составляющая центробежной силы S, представляет собой периодическую силу S (t ) S cos t вызывающая поперечные колебания балки в вертикальной плоскости. Частота силы S(t) n 30 3,14 400 41,86c 1 30 Динамический коэффициент K д 1 1 ( )2 2,28 Максимальное значение центробежной силы S P 2 e 1,2 41,86 2 0,028 58,87кН g 9,8 Наибольший динамический прогиб балки в сечении где расположен двигатель, в точке С д S C K д 58,87 103 2615 10 9 2,28 0,35 10 3 м Наибольший статический прогиб cт C Q 2615 10 9 120 10 3 0,314 10 3 м Наибольший полный прогиб max д cт 0.35 0.314 10 3 0.664 10 3 м Наибольшие динамические напряжения д M д S K д 0,432 58,87 103 2,28 0,432 202МПа W W 2 143 10 6 Наибольшие статические напряжения ст M ст Q 0,432 120 103 0,432 180МПа W W 2 143 10 6 Наибольшие полные напряжения п д ст 402МПа 280МПа условие прочности не выполняется, необходимо увеличить сечение балки Двутавр №20 Wx 184см 3 ; J x 1840см 4 c 13,436 13,436 1825,5 10 9 м/н 11 EI 2 10 1840 2 10 8 C C c 1836,5 10 9 м/н 0 g 9,8 66,68c 1 3 9 Q C 120 10 1836,5 10 Kд 1 1 ( )2 1,65 д S C K д 58,87 10 3 1836,5 10 9 1,65 0,18 10 3 м cт C Q 1836,5 10 9 120 10 3 0,15 10 3 м max д cт 0.18 0.15 10 3 0.33 10 3 м д M д S K д 0,432 58,87 10 3 1,65 0,432 114МПа W W 2 184 10 6 ст M ст Q 0,432 120 103 0,432 70МПа W W 2 184 10 6 Наибольшие полные напряжения п д ст 184МПа 280МПа условие прочности ыполняется, окончательно принимаем балку из двух двутавров №20 Прогибы балки изменяются по закону max f (t ) ст д 0.15 0.18 cos(41,86t) Напряжения изминяются по закону п д ст 70 114 cos(41,86t) Графики этих функций покажем на рисунке