МОДЕЛИРОВАНИЕ И АНАЛИЗ ТРЕХФАЗНОГО АСИНХРОННОГО

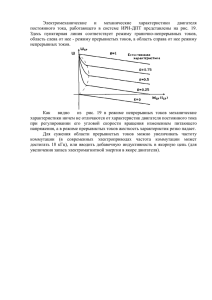
ІНФОРМАЦІЙНІ СИСТЕМИ І МОДЕЛЮВАННЯ
УДК 621.313.332
МОДЕЛИРОВАНИЕ И АНАЛИЗ ТРЕХФАЗНОГО АСИНХРОННОГО ГЕНЕРАТОРА С
ВЕНТИЛЬНО-ЕМКОСТНЫМ ВОЗБУЖДЕНИЕМ И АМПЛИТУДНО-ФАЗОВЫМ
РЕГУЛИРОВАНИЕМ РЕАКТИВНОГО ТОКА
Мазуренко Л. И., Лесник В. А., Джура А. В., Дынник Л.Н
Институт электродинамики НАН Украины
Введение. Электрификация отдаленных и
труднодоступных
населенных
пунктов
традиционным способом путем строительства
протяженных линий электропередач требует
больших капитальных затрат и связана, в
дальнейшем, с большими потерями в сетях. Более
экономически выгодно
для таких территорий
строить
малые
автономные
энергосистемы,
рассчитанные на потребности данной местности.
Электрооборудование малых сетей, прежде всего
генераторы, ввиду его изолированности должно
быть максимально надежным и отличаться
простотой в обслуживании [3].
Автономные асинхронные генераторы (АГ)
хорошо отвечают этим требованиям. Внимание
исследователей
[4]
в
последние
годы
сосредоточилось на разработке эффективных систем
возбуждения (СВ) АГ, позволяющих обеспечить
хорошее качество электроэнергии на стороне
потребителя. С изменением величины нагрузки для
поддержания требуемой величины напряжения
генератора СВ должна по определенному закону
регулировать ток намагничивания машины и
обладать симметрирующими свойствами для
снижения несимметрии напряжений и токов фаз АГ
при несимметричной нагрузке.
Системы возбуждения (источники реактивной
мощности) на основе конденсаторов постоянной
либо
дискретно
регулируемой
емкости,
индуктивностей с регулируемым насыщением,
компаундирующих
конденсаторов
не
могут
эффективно решать данные задачи. Наиболее
перспективными, ввиду больших успехов в области
развития полупроводниковой техники, считаются
вентильные и вентильно-емкостные источники
реактивной
мощности,
включающие
преобразователи на IGBT или MOSFET элементах.
Такие преобразователи обычно выполняются по
схеме одно- или трехфазного мостового инвертора
напряжения (ИН). Величину реактивной мощности
АГ изменяют с помощью частотного или фазового
регулирования преобразователя либо амплитуднофазового регулирования (АФР) тока [2,4].
Амплитудно-фазовое регулирование выходного тока
источника
реактивной
мощности
позволяет
контролировать токи ключей ИН и не допускать их
выхода за допустимые пределы.
В известных на настоящий момент публикациях
моделирование АГ с АФР реактивного тока
проводилось с помощью специализированных
пакетов программ SPEED [2], MATLAB [3] и
SABER [4] с использованием математической
модели машины в системе координат d, q.
Математические
модели
(ММ)
АГ
в
преобразованных системах координат не совсем
адекватно отображают электромагнитные процессы,
происходящие
в
машине,
особенно
при
выпрямительной и несимметричной нагрузках.
Одним из следствий использования таких моделей
является завышение расчетной мощности АГ [2].
Модель системы автоматического регулирования
(САР) в отмеченных работах [2-4] практически не
раскрыта, в результате чего нельзя установить вид
передаточных функций и оптимальные значения
постоянных времени в контурах обратных связей
САР.
Цель работы - разработка более эффективной,
чем известные, ММ АГ с вентильно-емкостным
возбуждением (ВЕВ) и АФР реактивного тока для
анализа возможных режимов работы генератора.
Материал и результаты исследований.
Расчетная схема генератора, представленная на
рис. 1 (рис. 1а – силовая часть, 1б – САР), содержит
асинхронную машину (АМ), обмотки которой
соединены в треугольник, трехфазную нагрузку,
батарею конденсаторов возбуждения, трехфазный
мостовой ИН, подключенный к АМ через
фильтрующие
дроссели
с
внутренним
сопротивлением rL и САР.
Модель электрической машины
АМ
описывается
системой
алгебродифференциальных уравнений в фазной системе
координат А, В, С, неподвижной относительно
статора с учетом насыщения магнитопровода [1].
Уравнения емкостной части СВ
Токи конденсаторов C A и C B на основании
законов Кирхгофа равны:
i KA  iC1  i KC ;
i KB  iC 2  i KA ,
откуда, выражая токи
через
i KA , i KB , i KC
напряжения, приходим к системе ДУ:
C B iC1  CC iC 2
dU A

,
dt
C A CC  C A C B  C B CC
C AiC1  C A  CC iC 2
dU B

,
dt
C A CC  C A C B  C B CC
где iC1  iC  i A  i HA  i HC  iCAИ ;
iC 2  i A  i B  i HA  i HB  i ABИ .
Уравнения нагрузки
Закономерность изменения токов трехфазной
активно-индуктивной нагрузки АГ определяется
системой ДУ
diHA
1
 u A  rHAi HA 
,
dt
LHA
diHB
1
 u B  rHB i HB 
,
dt
LHB
Вісник КДПУ. Випуск 3/2006 (39). Частина 1.
116
ІНФОРМАЦІЙНІ СИСТЕМИ І МОДЕЛЮВАННЯ
duСФ k1iСАИ  k 3i ABИ  k 5 i ABИ  iСАИ 
.

dt
CФ
Моделирование САР вентильной части СВ
Для стабилизации выходного напряжения АГ
САР содержит цепь отрицательной обратной связи
по амплитуде напряжения на нагрузке, величина
которой определяется через измеренные фазные
напряжения на каждом шаге интегрирования из
выражения
2 2
(1)
um 
u A  u B2  uC2 .
3
Величина
фактической
амплитуды
um
сравнивается с заданной амплитудой напряжения
U N . Их разность поступает на вход ПИ-регулятора
k у2
с передаточной функцией k у1 
. Если ИН
T1 p  1
рассматривать как эквивалентный симметричный
трехфазный источник реактивного тока, собранный
по схеме “треугольник” из трех источников
переменного тока, то полученное на выходе ПИрегулятора значение сигнала можно принять равным
diHC
1
.
  u A  u B  rHC i HC 
dt
LHC
Математическая модель вентильной части СВ
Вентильная часть СВ собрана по схеме
трехфазного мостового ИН и описывается
уравнениями:
 CA  k1uCФ ,  AB  k 3uCФ ,  BC  k 5uCФ ,
di
1   CA  L CAИ  rLiCAИ ,
dt
di ABИ
 2   AB  L
 rL i ABИ ,
dt
di
 3   BC  L BCИ  rLi BCИ ,
dt
i ABИ  iСAИ  i ВСИ  0 ,
du
iCФ  СФ CФ ,  2  u A  1 ,  3  u B   2 ,
dt
где
коммутационные
функции,
k1 , k 3 , k 5 принимающие значения 0 или 1 в зависимости от
того, закрыт либо открыт соответствующий ключ
( S1 , S 3 , S 5 ). Ключи S 2 , S 4 , S 6 переключаются в
2
d
3
Ур.№3
Ур.№1
S1
S2
S5
i САИ
iА
L
iС
1
k1
k3
k5
rL
3
i АВИ
L
rL
L
rL
AB
h
BC
S2
UN
Ур.№6
CA
Сф
UB UC
k 3H k 5H
k 1H
w

i АВИ i ВСИ i САИ UA
АМ
iВ
ИН

S6
S4
i ВСИ
Z HA
Z HC
i HА
Z HB
i HC
i HB
Н
3
Ур.№7
PI
Ур.№2
Ур.№4
i C1
i C2
i KА
i KC
Ур.№5
E
СA
Определение
dА , dB , dC
3
СC
i KB С
B
Определение
qА, qB , qС
3
САР
БК
б)
a)
Рисунок 1 - Схема силовой части АГ с ВЕВ (а) и САР реактивного тока ИН (б)
амплитуде заданных
преобразованных токов
i АИР , i ВИР , iСИР в каждой фазе этого источника:
противофазе
по
отношению
к
S1 , S 3 , S 5 .
Соответственно в каждой стойке всегда один из
ключей открыт, а другой заперт. Записанные
уравнения сводятся к системе ДУ в форме Коши:
di ABИ uСФ k 5  2k 3  k1   3rL i ABИ  u A  u B

,
dt
3L
diCAИ uСФ k 5  k 3  2k1   3rL iCAИ  2u A  u B

,
dt
3L
k у2 

U N  u m  .
im p   k у1 
T1 p  1 

Мгновенные расчетные значения заданных
преобразованных токов
зависят от величины и
знака im p , а также угла поворота  вектора
напряжения фазы A АГ:
Вісник КДПУ. Випуск 3/2006 (39). Частина 1.
117
ІНФОРМАЦІЙНІ СИСТЕМИ І МОДЕЛЮВАННЯ


i АИР  imp sin    ,
2



(2)
i ВИР  imp sin    ,
6

7 

iСИР  i mp sin  
.
6 

Величина угла  должна изменяться в пределах
  ,   и с учетом допущения о синусоидальности
напряжений u A , u B , uC может быть определена из
выражения:
2 sgnu B  uC 
u
,
(3)
  arcsin A 
1
um  
uA 
 sign u A  arcsin

u m 
2
где sgn x  1 для x  0 , и sgn x  0 для x  0 , x действительное число.
Таблица 1 Характер изменения токов i АИ , i ВИ , iСИ для
различных состояний вектора потенциалов
ИН на интервале для которого выполняется
условие u A  0, u B  0, uC  0
CA
AB
+
+
+
+
-
Текущие преобразованные токи ИН в 3 раз
меньше по амплитуде текущих выходных токов ИН
iАВИ , iВСИ , iСАИ и связаны с ними соотношениями:
+
+
+
+
BC
+
+
+
+
i АИ
i BИ
i CИ
И/НИ
H
H
B
И
H
H
B
НИ
H
B
B
И
H
H
B
НИ
H
H
B
НИ
H
B
H
И
B
H
B
И
B
H
H
И
обозначает
равенство
данного
потенциала
потенциалу  d , а "" - потенциалу  E . Под
характером изменения токов подразумевается их
возрастание (В), т. е. значение становится более
1
2
i АИ   i ВСИ  i АВИ ,
3
3
1
1
(4)
i ВИ   i ВСИ  i АВИ ,
3
3
2
1
iСИ  i ВСИ  i АВИ .
3
3
Сравнивая
значения
соответствующих
преобразованных заданных и преобразованных
текущих токов ИН, часть САР, обычно называемая
контроллером
тока,
должна
формировать
управляющие сигналы для ключей ИН таким
образом, чтобы разность фактических и расчетных
токов удерживалась в пределах гистерезисной
полосы  I h . Метод формирования управляющих
сигналов, при котором траектория изменения тока
ИН ограничена гистерезисной полосой (метод
гистерезисного контроля тока) прост в реализации и
обеспечивает
высокие
динамические
характеристики [5]. Одним из основных недостатков
этого метода является то, что регулирование
каждого из выходных токов ИН осуществляется
ключами соответствующих стоек независимо от
характера изменения других токов. В результате
отсутствует стратегия формирования нулевого
вектора коммутационного состояния ИН (когда
одновременно включены все ключи катодной или
анодной
групп)
и
частота
переключения
транзисторов оказывается завышенной.
Для осуществления взаимосвязанного контроля
токов i АИ , i ВИ , iСИ , рассмотрим, как характер
изменения этих токов зависит от вектора
потенциалов  АВ ,  ВС ,  СА  - на различных
интервалах времени, в пределах которых фазные
напряжения не изменяют знак. Возможные
состояния вектора потенциалов и его влияние на
токи i АИ , i ВИ , iСИ для интервалов работы АГ при
u A  0, u B  0, uC  0 отражены в табл.1. Здесь ""
[В]
500
uAИ
uA
0
-500
1.87
1.88
[А]
а)
1.89
t,с
iA
iAИ
5
1.9
0
-5
1.87
1.88
1.89
1.9
t,с
б)
Рисунок 2 - Фазное напряжение АГ и
напряжение ИН  AB   CA (а),
преобразованный ток ИН и ток АМ одной из
фаз (б)
положительным, или уменьшение, т. е. значение
становится более отрицательным (Н). Как видно из
табл. 1, существуют состояния вектора потенциалов,
приводящие к одинаковому характеру изменения
токов. Среди них нужно выбирать одно, отдавая
приоритет тому, которое (с целью снижения
Вісник КДПУ. Випуск 3/2006 (39). Частина 1.
118
ІНФОРМАЦІЙНІ СИСТЕМИ І МОДЕЛЮВАННЯ
iСАИР  i АИР  iСИР ;
(7)
i АВИР  i ВИР  i АИР ;
i ВСИР  iСИР  i ВИР .
В качестве примера, для АГ, выполненного на
базе асинхронного двигателя 4АМА100S2У3, на
рис.3а показаны результаты расчета фазного
напряжения u A и напряжения на зажимах ИН
 AB   CA  u АИ , а на рис.3б - тока в фазе А
машины и преобразованного тока ИН i АИ (ИН
работает в режиме генерирования реактивной
мощности).
Выводы. Разработанная математическая модель
позволяет точнее, чем в более ранних публикациях,
исследовать динамические и квазиустановившиеся
режимы АГ с ВЕВ и АФР реактивного тока. Для
снижения
частоты
переключения
в
САР
использованы логические выражения, позволяющие
эффективнее
использовать
нулевой
вектор
коммутационного
состояния
ИН.
Детальное
исследование переходных и установившихся
процессов как в симметричном, так и в
несимметричном режимах будет проведено в
дальнейших публикациях.
частоты коммутации) исключает конденсатор СФ
из контуров протекания тока. По этой причине
состояния вектора потенциалов с номерами 2 и 4 на
данном интервале постоянства знаков фазных
напряжений не будут
использованы (НИ) как
дублирующие по результату воздействия на токи
состояние 1, обеспечивающее
i АИ , i ВИ , iСИ
меньшую скорость изменения токов. Пятое и первое
состояния отвечают одинаковым схемам замещения
инвертора и для моделирования не имеет значения,
какому из них отдавать приоритет. Также можно
заметить, что ни одно из возможных состояний
вектора потенциалов не может обеспечить
одновременное повышение токов i АИ и i ВИ . На
других интервалах также невозможно обеспечить
увеличение (уменьшение) тех двух токов, для
которых соответствующие фазные напряжения
имеют одинаковый знак.
После
рассмотрения
оставшихся
пяти
интервалов
постоянства
знака
напряжений
генератора получаем логические выражения,
описывающие коммутационные функции ключей
S1 , S 3 , S 5 ИН для произвольного момента времени:
k1  g11  g12 , k3  g 31  g 32 , k5  g 51  g 52 , (5)
где
g11  d A d B q A  q B qC  d B  d C ,

 


где
ЛИТЕРАТУРА
1. Лесник В.А., Мазуренко Л.И., Джура А.В.,
Дынник Л.Н. Математическая модель и алгоритм
расчета режимов однофазного асинхронного
генератора с вентильно-емкостным возбуждением.
//Технічна електродинаміка-2005.-№3.- С.44-48.
2. M. Naidu, J. Walters, “ A 4-kW 42V inductionmachine-based automotive power generation system
with a diode brige rectifier and a PWM inverter”, IEEE
Transactions. on Industry Applications, Vol. 39,
Sept./Oct. 2003, pp. 1287-1293.
3. S. A. Daniel, N. A. Gounden, ”A novel hybrid
isoleted generating system based on PV fed inverterassisted wind-driven induction generators”, IEEE
Transactions on Energy Conversion, vol. 19, no. 2,
June 2004, pp. 416-421.
4. S. Wekhande, V. Agarval, ”Simple control for a
wind-driven induction generator”,
IEEE Industry
Applications Magazine, March/April 2001, pp. 45-54.
5. J. Holtz, “Pulsewidth modulation for electronic
power conversion”, Proceedings of the IEEE, Vol. 8,
August 1994, pp. 1194-1214.

g12  q A d A d C  q B qC d B   q B qC d B d C ,
g 31  d A d C  d B  q A  q B qC ,


 


g 51  d A d B q A q B  q AqC   q A q B   d B d C ,
g 52  d A d C q A q B  q AqC   q AqC  .
g32  q A q B qC d Ad C  qC d B d C  d A d B ,
Переменные d A , d B , d C , q A , q B , qC - дискретные
функции,
определяемые
из
выражений
d A  sgni АИР  i АИ  ,
d В  sgni ВИР  i ВИ  ,
d С  sgniСИР  iСИ  , q A  sgnu A  , q B  sgnu B  ,
Коммутационные
функции
qC  sgnuC  .
k1 , k 3 , k 5 , а также k CA , k AB , k BC - “гистерезисные”
функции, индицирующие о нахождении разности
соответствующих расчетных и фактических токов
ИН в пределах (сигнал равен нулю) или вне (сигнал
равен единице) гистерезисной полосы, поступают на
гистерезисные элементы, которые могут быть
выполнены на RS или D триггерах. Каждый
гистерезисный элемент передаёт сигнал ki , i  1,3,5
со своего входа на выход без изменения, когда
соответствующая
“гистерезисная”
функция
( k CA , k AB , k BC ) равна единице, либо сохраняет
предыдущее значение, когда она равна нулю.
“Гистерезисные”
функции
определяются
из
выражений:
kCA  sgn iCAИ  iСАИР  I h ,


k AB  sgni АВИ  i АВИР  I h  ,
k ВС  sgni ВСИ  i ВСИР  I h  ,
Стаття надійшла 18.04.2006 р.
Рекомендована до друку
д.т.н., проф. Родькіним Д.Й.
(6)
Вісник КДПУ. Випуск 3/2006 (39). Частина 1.
119