Документ 733405
реклама
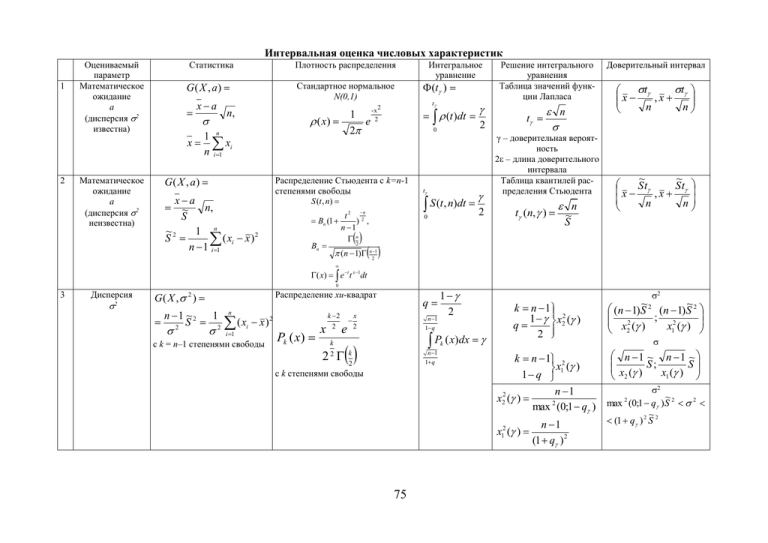
Интервальная оценка числовых характеристик 1 2 Оцениваемый параметр Математическое ожидание а (дисперсия 2 известна) Математическое ожидание а (дисперсия 2 неизвестна) Статистика Плотность распределения G ( X , a) xa Стандартное нормальное N(0,1) 2 1 n x xi n i 1 G ( X , a) xa n, ~ S 1 n ~ S2 ( xi x ) 2 n 1 i 1 S (t , n) n t2 2 Bn (1 ) , n 1 n2 Bn (n 1) n21 t 0 Распределение Стьюдента с k=n-1 степенями свободы (t ) (t )dt 1 - x2 ( x) e 2 n, Интегральное уравнение t 2 S (t , n)dt 2 0 Решение интегрального уравнения Таблица значений функции Лапласа t n γ – доверительная вероятность 2ε – длина доверительного интервала Таблица квантилей распределения Стьюдента n t (n, ) ~ S Доверительный интервал t t x , x n n ~ ~ S t S t x ,x n n ( x) e t t x 1dt 0 3 Дисперсия 2 Распределение хи-квадрат G( X , ) 2 n 1 ~ 1 2 S2 2 n (x x) i 1 i с k = n–1 степенями свободы 2 Pk ( x) x k 2 2 k 2 x 2 n 1 1 q n 1 1 q e 2 q 1 2 P ( x)dx k n 1 1 x22 ( ) q 2 k n 1 2 x1 ( ) 1 q n 1 x22 ( ) 2 max (0;1 q ) n 1 ~ n 1 ~ x ( ) S ; x ( ) S 2 1 k k 2 с k степенями свободы x12 ( ) 75 2 ~ ~ (n 1) S 2 (n 1) S 2 2 x ( ) ; x 2 ( ) 1 2 n 1 (1 q ) 2 2 ~ max 2 (0;1 q ) S 2 2 ~ (1 q ) 2 S 2 Интервальное оценивание нормально M a; T x 2 Дисперсия известна Оцениваемый параметр M a; T x Дисперсия 2 неизвестна 1 n s ( xi x ) 2 n 1 i 1 N (a; 2 ) или асимптотически нормально распределённого признака : P(T T ) при доверительной вероятности с точностью Табличные значения из приложений В.Е. Гмурмана t (t ) (t )dt 0 t D ; x t ( ) из приложения 2 2 2 S (t , n)dt 2 t ( 2 ; n 1) ; t ( , n) из приложе- ния 3 x22 ( 1 , n 1) ; 2 x12 ( 1 , n 1) из приложения 5 2 t (t ) (u )du 0 показательного распределения С.В. 1 1 M a ; D 2 (t ) (t )dt распределения Пуассона t P( x) x x! exp( ) t 0 (t ) (t )dt 0 t ( ) из приложения 2 2 2 t ( ) из приложения 2 2 2 где s t n 22 a x ax 2 t n s t n (n 1) s 2 12 max 2 (0;1 q ) s 2 2 (1 q )2 s 2 t ( ) из приложения 2 2 2 Замечание. При малом объёме выборки (n 30) и бесповторном отборе точность n (n 1) s 2 q ( , n) из приложения 4 p – вероятность успеха в n испытаниях Бернулли; m – доля n t x 0 2 2 Доверительный интервал n t2 (1 ) t t ( )2 2 t n 2n n 2n (1 ) n 100; 1, 2 t n xt xt t t 1 1 x a x ; (1 )1 (1 )1 n n x n x n t t t t 1 1 x exp( a x exp( ) ; exp( ) exp( ) n n x n x n t t x x 2 n 2 n n 100; 1, 2 следует умножить на поправку N – объём генеральной совокупности. 76 1 n , N Гипотеза о независимости 2-х признаков Гипотеза проверки однородности двух выборок Критерий Смирнова Эмпирические функции распределения: F1,n, и F2,m n, m – объёмы выборок Статистика критерия Dnm max F1, n ( x) F2, m ( x) x Наблюдаемое значение критерия λнабл nm Dnm nm набл. Критерий Вилкоксона ( n1 n2 ) Расположить выборки в виде одного вариационного ряда (n1 – объём первой выборки, n2 – объём второй выборки); ωнабл. – сумма порядковых номеров первой выборки в образованном вариационном ряду Альтернативные Основная гипотеза H 0 : F1 ( x) F2 ( x) гипотезы Кр.Вилкоксона n n 25 n 25 n 25 1 H1 : F1 ( x) F2 ( x) –двусторонняя критическая область 2 н.кр .т. (Q , n1 , n 2 ) 2 н.кр .т. из P( nm Dnm кр . ) K (кр . ) nm 1 2 (1) j e Гипотезы Смирнова H 0 : F1 ( x) F2 ( x) H1 : F1 ( x) F2 ( x) 2 j 2кр 2 1 j 1 набл. кр . Н 0 принимают набл. кр . Н 0 отвергают Критерий Кендалла А 1 2 … n Rk – число рангов, В y1 y2 … yn больших yk Статистика критерия R=R1+R2+…+Rn-1 Выборочный коэфф. ранговой корреляции Кендалла τв Критическая точка Ткр в 4R 1 n(n 1) H1 : F1 ( x) F2 ( x) - таблицы критических точек критерия Вилкоксона –левосторонняя критическая область правосторонняя критическая область А В Tкр z кр R1 S1 R2 S2 лицы критических точек критерия Вилкоксона в.кр .т. (n1 n 2 1)n 1 н.кр .т … … Rn Sn Статистика критерия Выборочный коэфф. ранговой корреляции Спирмена набл rв n2 1 rв2 Критическая точка t кр ( , n 2) 1 ( z кр ) 2 Гипотезы Кендалла H 0 : в 0; Н1 : в 0 из таб- (n1 n2 1)n1 1 n n (n n2 1) z кр . 1 2 1 ; 2 12 н.кр .т. 1 2 функция Лапласа; 2 (n1 n2 1)n1 н.кр .т ( z кр . ) в.кр .т Выборочный коэфф. ранговой корреляции Спирмена ρв n rв i i 1 n i n DR DS i 1 2 i i 1 Н0 принимают, если ωнабл. < ωв.кр.т. Т – ранги выборки по признаку В d i i Ti в 1 6 n(n 2 n d 1) i 1 2 i 2 i t кр ( , n 2) – из таблицы рас- пределения Стьюдента (двусторонняя критическая область) в Tкр Гипотезы Спирмена Н0 принимают, связь признаков незначимая H 0 : rв 0; Н0 принимают, связь признаков незна- Н 1 : rв 0 чимая Т набл tкр 77 Н0 принимают, если ωнабл. > ωн.кр.т. (n n 1)n1 1 n n (n n 1) 1 2 zкр . 1 2 1 2 ; 2 12 1 2 ( zкр . ) функция Лапласа; 2 Критерий Спирмена А 1 2 … n R, S – ранги выборки по приВ T1 T2 … Tn знакам А и В Статистика критерия DRi Ri R; DS i Si S DR DS Н0 принимают, если ωн.кр.т. < ωнабл. < < ωв.кр.т. н.кр .т. из таб- лицы критических точек критерия Вилкоксона H1 : F1 ( x) F2 ( x) -– н.кр .т. (Q , n1 , n2 ) rв Т 2(2n 5) 9n(n 1) н.кр .т. (Q , n1 , n2 ) 2 (n n2 1)n1 1 n n (n n2 1) 1 z кр . 1 2 1 ; 2 12 1 ( z кр . ) функция Лапласа; 2 в.кр .т (n1 n2 1)n1 н.кр .т в.кр .т. (n1 n 2 1)n 1 н.кр .т Критическая точка λкр.распределения Колмогорова К(λ), α – уровень значимости 1 Критическая точка 1 в2 Tкр t кр ( , n 2) n2 Гипотезы Спирмена H 0 : в 0; Н1 : в 0 t кр ( , n 2) – из таблицы распреде- ления Стьюдента (двусторонняя критическая область) в Tкр Н0 принимают, связь признаков незначимая Сравнение двух средних генеральных совокупностей. (независимые выборки) I I H0: mx=my α – уровень значимости Нормальное распределение. Dx,Dy известны Т набл Да xy Н1: mx> my /2 /2 -tкр 0 tкр двусторонняя критическая область Ф(tкр)= Тнабл<tкр – tкр 0 левосторонняя критическая область 1 2 2 Тнабл<tкр да H0-отвергают, принимают Н1 Н1: mx< my 0 tкр правосторонняя критическая область 1 2 нет Смотри II Конкурирующая гипотеза Н1 Dx D y nx n y Н1: mx my Ф(tкр)= Нет Нет n>30 нет Тнабл>─ tкр нет да да нет H0-принимается 78 H0-отвергают, принимают Н1 Сравнение двух средних генеральных совокупностей. (независимые выборки) II II H0: mx=my α – уровень значимости Распределение Стьюдента. Dx,Dy -неизвестны да нет Смотри I n>30 Распределение Фишера-Снедекора F набл = Н0D: Dx= Dy ~ S x2 ~ S y2 Конкурирующая гипотеза Н1D ~ S x max( S x , S y ) Fкр=F(,k1,k2) k1=nx–1, k2=ny–1 Н1D: Dx Dy Н1D: Dx> Dy Fкр=F( 2 ,k1= nx–1,k2= ny–1) Fнабл<Fкр да нет H0D-принимается Dx=Dy k=nx+ny – 2 ~2 ~ S x2 S y 2 ( ) nx n y k ~ ~ S y2 2 S x2 2 ( ) ( ) ny nx nx 1 n y 1 H0D-отклоняется, принимается H1D tkr (α, k) находят по распределению Стьюдента n x n y (n x n y 2) xy Tнабл= ~ ~ nx n y (n x 1) S x2 (n y 1) S y2 Tнабл= xy ~2 ~ S x2 S y nx n y Конкурирующая Н1 Н1: mx my двусторонняя область двусторонняя критическая область критическая Тнабл<tкр нет Н0-отвергается да Н1: mx> my односторонняя область Н1: mx< my односторонняя область односторонняя критическая область критическая нет односторонняя критическая область критическая нет Тнабл<tкр да да Тнабл>– tкр нет Н0-принимается 79 Н0-отвергается Проверка гипотезы о равенстве вероятностей событий в испытаниях по схеме Бернулли m m m m2 ; Нулевая гипотеза H 0 : p1 p 2 ; w1 1 ; w2 2 ; w 1 n1 n2 n1 n2 p1q1 pq ) w2 N ( p2 ; 2 2 ) (n1, n2 100) n1 n2 Очевидно, что если испытания независимы в пределах каждой выборки и между выборками, то величины m1 и m2 независимы, тогда w1 и w2 также независимы. Поэтому w1 N ( p1 ; p1q1 p2 q2 ) n1 n2 ( w1 w2 ) ( p1 p 2 ) N (0; 1) p1 q1 p 2 q 2 n1 n2 Следовательно, проверка нулевой гипотезы осуществляется при помощи критерия w1 w2 N ( p1 p2 ; w1 m1 m m m2 ; w2 2 ; w 1 ; u набл. n1 n2 n1 n2 Альтернативная гипотеза а H1 : p1 p2 в H1 : p1 p2 w(1 w)( Критические точки 1 (u крит ) 2 1 2 (u крит ) 2 1 2 (u крит ) 2 H1 : p1 p2 б w1 w2 1 1 ) n1 n2 Правило принятия решения: Н0 отклоняется, если u набл u двустор крит; u набл u 2 правостор крит; левостор u набл u крит ; Следствие. Проверка гипотезы о численном значении вероятности события в испытаниях по схеме Бернулли Нулевая гипотеза H 0 : p p0 w m ; u набл. n w p0 p0 (1 p0 ) Альтернативная гипотеза а H1 : p1 p0 б H1 : p1 p0 в H1 : p1 p0 1 n Критические точки 1 (u крит ) 2 1 2 (u крит ) 2 1 2 (u крит ) 2 80 Правило принятия решения: Н0 отклоняется, если u набл u двустор крит; u набл u 2 правостор крит; левостор u набл u крит ; H0 H0 : 1 2 Сравнение дисперсий сравнение двух дисперсий Тестирование параметрических гипотез Критические точки H Статистика 1 H1 : 1 2 Распределение Фишера F ( 1 2 ) 12 22 H1 : 1 2 H0 : 0 сравнение выборочной дисперсии с генеральной дисперсией (n 1) s 2 Сравнение с генеральной средней (сравнение двух средних см. ОК С. 78, 79). 2 2 , n 1) ďđŕâ. ęđ ( , n 1) 2 2 2 íŕáë . ëĺâ . ęđ (1 , n 1) 2 или 2 2 íŕáë . ďđŕâ. ęđ ( , n 1) 2 H1 : 0 ęđ2 ( , n1) 2 2 íŕáë . ęđ ( , n 1) H1 : 0 ęđ2 (1 , n1) 2 2 íŕáë . ęđ (1 , n1) H1 : a a0 t äâóńň. ęđ . ( , n 1) Tíŕáë t äâóńň. ęđ . ( , n 1) H 1 : a a0 t ďđŕâîńň . ęđ . ( , n 1) Tíŕáë t ďđŕâîńň . ęđ . ( , n 1) ная средняя) ( x a0 ) Tíŕáë . n s H 1 : a a0 t ďđŕâîńň . ęđ . ( , n 1) Tíŕáë t ďđŕâîńň . ęđ . ( , n 1) H 0 : a1 a0 N (0; 1) H1 : a1 a0 1 2 1 2 (u крит ) 2 1 2 (u крит ) 2 1 (uęđčň ) 2 1 2 (u крит ) 2 1 2 (u крит ) 2 1 (u крит ) 2 1 2 (u крит ) 2 1 2 (u крит ) 2 u набл u двустор H 0 : a a0 дисперсия неизвестна ( a 0 - генераль- дисперсия известна ( a 0 - генераль- Распределение Стьюдента u íŕáë . ная средняя) H 0 : p1 p2 Сравнение вероятностей 2 2 0 Мощность критерия Fíŕáë Fkp ( , n1 1, n2 1) Fkp ( , n1 1, n2 1) ëĺâ . ęđ (1 2 íŕáë . kp ( , n1 1, n 2 1) 2 Привести к случаю 2 H1 : 0 2 Fíŕáë F kp ( , n1 1, n 2 1) 2 H1 : 1 2 Распределение F Н0 отклоняется, если сравнение двух вероятностей в испытаниях по схеме Бернулли H 0 : p p0 (u крит ) H :a a ( x a0 ) n 1 1 0 H1 : a1 a0 w1 m1 ; n1 w2 H1 : p1 p2 m2 ; n2 m m2 w 1 ; n1 n2 u íŕáë . w(1 w)( w H1 : p1 p2 w1 w2 1 1 ) n1 n2 H1 : p1 p2 H 1 : p p0 m ; n сравнение вероятности в испытаниях по схеме Бернулли с гипотетической p 0 u íŕáë . H 0 : a1 a0 H 1 : a1 a 0 H 1 : p p0 w p0 p0 (1 p0 ) H 1 : a1 a0 1 n H 1 : p p0 M 1 0.5 (uęđ M 1 1 (u ęđ (u ęđ a1 a 0 n) 81 a1 a0 a1 a 0 n) n) крит; u набл u 2 правостор крит; левостор u набл u крит ; uíŕáë u äâóńňîđ ęđčň ; u набл u 2 правостор крит; левостор u набл u крит ; u набл u двустор крит; u набл u 2 правостор крит; левостор u набл u крит ; 1 2 2 1 (u ęđ ) 2 (u ęđ ) ( xi Проверка гипотезы о распределении генеральной совокупности по критерию Пирсона m Значения вариант xi x1 x2 …… x m n ni – объём вы– середины интервалов (ci ; ci 1 ); i 1, ..., s : i 1 борки; (ci 1 ci ) xi xi 1 xi h – шаг. 2 для непрерывных распределений) Выборочные частоты ni n1 Интервалы, содержащие малочисленные частоты …… n2 nm (ni 5) , объединяют с соседними интервалами, а частоты в этих интервалах складывают; s – число интервалов после сложения малочисленных частот; r – число параметров, вычисляемых по выборке; k s r 1 – число степеней свободы; npi – теоретические частоты. Наблюдаемое значение статистики критерия 2 íŕá ęđ2 ( , k ) при уровне значимости . Критическая точка – квантиль распределения Пирсона Нулевая гипотеза Распределение Нормальное H 0 : выборка принадлежит ……………. распределению. Теоретические частоты nh ( xi x) 2 npi exp( ) 2 2 2 (выборка задана вариантами xi ) 1 ni xi ; n i среднее квадратическое отклонение 1 xi2ni ( x)2 n i Показательное 1 x (x 1 ni xi ) n i Биномиальное P x m (x 1 ni xi ) n i Равномерное npi n( ( (x 1 ni xi ; n i x (x ci 1 x ) ( ci x )) (выборка задана интервалами (ci ; ci 1 ); i 1, ..., s , c1 ; c s 1 ) npi n(exp( ci ) exp( ci 1 )) (выборка задана интервалами (ci ; ci 1 ); i 1, ..., s ) npi nC si P i (1 P) s i (выборка задана вариантами 0, 1, …, a x 3 ; b x 3 Пуассона правосторонней критической области Параметры, вычисляемые по выборке Выборочное среднее x (ni n pi ) 2 . n pi 1 xi2 ni ( x) 2 ) n i m) b c s 1 c1 a ; np s n ; ba ba c ci 1 np 2 np3 ... np s 1 n i ba (выборка задана интервалами (ci ; ci 1 ); i 1, ..., s ) np1 n 1 ni xi ) n i npi n i exp( ) i! (выборка задана вариантами 0, 1, …, Гипотеза о виде распределения принимается, если 2 íŕá m) . 2 ęđ При расчётах вручную рекомендуется составить таблицу i ni npi ni n pi 82 ( ni n p i ) 2 ( ni n p i ) 2 n pi Алгоритм расчётов по проведению однофакторного дисперсионного анализа вручную 1. Показать возможность применения к экспериментальным данным дисперсионного анализа при уровне значимости применив критерий Бартлетта. H 0 : D1 D2 ... D p ; q1 , q2 , ..., q p – количество наблюдений на уровнях , 2 A1 , A2 , ..., Ap соответственно; s 21 , s 2 , ..., s 2 p – исправленные дисперсии на уровнях A1 , A2 , ..., Ap соответственно. p s02 (qi 1) si2 i 1 p (q i i 1 1) 1 p s02 p Q ( q 1 ) ln íŕáë 1 1 1 i si2 Q 1 p i 1 3( p 1) i 1 qi 1 ( q 1 ) i i 1 (Пирсона) с (p–1) степенями свободы. где F(x) – функция распределения Хи-квадрат , , 1 Приодинаковом числе F (1 ) наблюдений на всех уровнях применить критерий Кочрена. ęđ 2. Найти средние для каждого уровня фактора 3. Составить расчётную таблицу, обозначив x j и общее среднее x . yij xij x отклонения наблюдений xij от общего среднего x . T j , Q j , T j2 - суммы отклонений и квадратов отклонений по столбцам расчётной таблицы. Пусть уровней фактора p 3 , число наблюдений на каждом уровне одинаковое q 4 . y1 y12 y2 n q1 q2 q3 A3 A2 A1 y22 y3 y pq 2 3 1 2 3 4 Qj Tj T1 T2 T3 T j2 T12 T22 T32 1. Q Q j Q3 Q2 Q1 T Tj T 2 Tj2 Найти суммы факторную, общую, остаточную: Côŕęň T2 T 2 ; q n C îáů Q T2 ; n Ńîńň Ńîáů Ńôŕęň . 2 sôŕęň Côŕęň 2 sîńň 2. Найти дисперсии факторную и остаточную: 3. Вычислить наблюдаемое значение статистики критерия Фишера Fíŕáë p 1 ; Ńîńň . n p s 2 ôŕęň . s 2 îńň 4. Найти критическую точку по таблице критических точек распределения Фишера – Снедекора Fęđ ( , p 1, n p 1) или функцией qF (1 , p 1, n p 1) в системе Маткад. 5. Принять или отклонить нулевую гипотезу о незначимом отличии факторной и остаточной дисперсий, т.е. о незначимом влиянии фактора. Замечание. При разном количестве наблюдений на разных уровнях фактора по-другому вычисляется только факторная сумма 2 Côŕęň Tp T 2 T2 T2 . Все остальные вычисления проводятся так же, как и при одинаковом количестве 1 2 ... q1 q2 qp n наблюдений на всех уровнях фактора. 83
