Zadacha_4-Kruchenie_vala

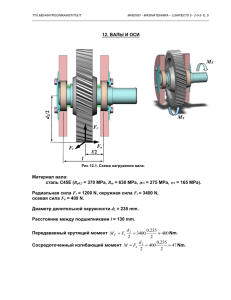
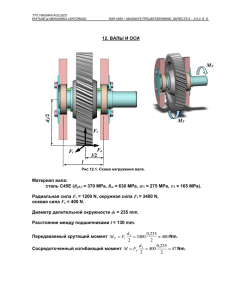
ЗАДАНИЕ 4
Кручение статически неопределимого вала
:
Ступенчатый вал круглого поперечного сечения (рис.3.1) имеет длину 6a.
Левая половина вала имеет диаметр d, правая - 2d . На расстоянии 2a от левой
заделки действует крутящий момент М, на расстоянии 2a от правой - момент
4M .
Рис.4.1. Ступенчатый статически неопределимый вал
M
100 kN m
Модуль сдвига:
a
G
1 m
5
10 MPa
Предел текучести при растяжении
T
250 MPa
Нормативный коэффициент запаса по касательному напряжению n
1.6
Принять, что предел текучести при сдвиге связан с пределом текучести при
растяжении как  T 0.6  T  T  150 MPa
Требуется:
1. Построить эпюры крутящих моментов.
2. Исходя из предела текучести по сдвигу и нормативного коэффициента запаса,
определить диаметр поперечного сечения d.
3. Построить эпюры углов закручивания для рассчитанного вала.
Решение
1. Сначала зададим некоторое значение диаметров вала. Например, d
По условию задачи D1 ( d ) 2 d D1 ( d )  20 cm
10 cm
1. Сначала запишем выражение для полярного момента инерции вала,
который изменяется по его длине при переходе от "тонкой" части к
"толстой".
 d
4
I( x  d )
32
if 0 x 3 a
 ( D1 ( d ) )
4
32
if 3 a x 6 a
Определим опорные реакции. Для этого зададим начальные приближения
1 kN m
R1
R2
1 kN m
Given
Уравнение равновесия:
R1
R2
M
4 M 0
Уравнение совместности деформаций (перемещение сечения А равно
нулю)
R1 3 L
GI ( a  d )
R1
R2
R1 3 L
GI ( 5 a  d )
ML
GI ( 2.5 a  d )
M3 L
GI ( 3.5 a  d )
4 M2 L
0
GI ( 5 a  d )
Find ( R1  R2 )
Опорные реакции определены:
Запишем по силовым участкам функцию, определяющую зависимость
крутящего момента от координаты сечения и построим эпюру крутящих
моментов (рис.4.2).
M x( x)
R1 if 0 x 2 a
R1
M if 2 a x 3 a
R1
M if 3 a x 4 a
R1
M
4 M if 4 a x 6 a
Введем ранжированную переменную х по длине вала
x
0 m 0.04 m 6 a
600
400
M x( x)
kN m
200
0
200
0
2
4
6
x
m
Рис.4.2. Эпюра крутящих моментов
2. Сформируем функцию для полярного момента сопротивления кручению
I( x  d )
if 0 x 3 a
0.5 d
W p( x d)
I( x  d )
if 3 a x 6 a
0.5 D1 ( d )
3. Запишем выражение для эпюры максимальных касательных
напряжений как зависимость от диаметра d (рис.4.3):
 max( x  d )
M x( x)
W p( x d)
500
 max( x d )
0
MPa
500
0
2
4
6
x
m
Рис.4.3. Вид эпюры максимальных касательных напряжений для
некоторого произвольного значения диаметра d
Максимальные напряжения имеют место при 4 a  x 6 a .
4. Найдем диаметр поперечного сечения D, при котором обеспечивается
назначенный коэффициент запаса по пределу текучести в этом диапазоне
изменения координаты х.
Для этого отыщем такие значения диаметра d 0 , при котором
соответствующее значение максимального касательного напряжения  max x  d 0
равно допускаемому напряжению  lim (по модулю).
 lim
T
n
Зададим начальное приближение:
d
Given
 max( 5 a  d )
D
10 cm
 lim
(Критериальное условие прочности)
Find ( d )
Найденное значения диаметра:
D  14.48 cm
Вновь задаем ранжированную переменную х по длине вала
x
0 m 0.09 m 6 a
и строим эпюру максимальных касательных напряжений уже для найденного
диаметра d0 (рис.4.4):
100
 max( x D )
50
MPa
 lim
MPa
0
 lim
MPa
50
100
0
2
4
6
x
m
Рис.4.4. Эпюра максимальных касательных напряжений
Из рис.4.4. следует, что максимальные касательные напряжения при d d 0
нигде не превышают  lim.
5. Переходим к построению эпюры углов закручивания. Для этого
предварительно вычислим относительные углы закручивания
отдельных силовых участков
2 a
1
M x( x)
1
I ( x  D)
G
dx
1  0.025
dx
2  0.011
0
3 a
2
M x( x)
1
G
2 a
I ( x  D)
4 a
3
M x( x)
1
G
3 a
I ( x  D)
dx
4
3  6.815 10
6 a
4
M x( x)
1
G
4 a
I ( x  D)
dx
4  0.013
Проверим правильность вычислений. Сумма углов закручивания на
отдельных участках должна быть равна нулю. И действительно
1
2
3
4  0 deg
Построим эпюру углов закручивания (рис.4.5):
x
 ( x)
M x( x)
1
I ( x  D)
G
d x if 0 x 2 a
0
x
1
M x( x )
1
G
2 a
I ( x  D)
d x if 2 a x 3 a
x
1
2
M x ( x)
1
G
3 a
I ( x  D)
d x if 3 a x 4 a
x
1
2
3
M x( x )
1
G
4 a
I ( x  D)
d x if 4 a x 6 a
0
( x)
deg
1
2
0
2
4
6
x
m
Рис.4.5. Эпюра углов закручивания; 1 rad  57.296 deg