«Геометрический смысл производной» УПРАЖНЕНИЯ ПО ТЕМЕ

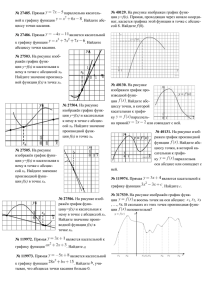
УПРАЖНЕНИЯ
ПО ТЕМЕ
«Геометрический смысл производной»
Составитель:
Горбаченко В.И.
учитель математики
МОУ СОШ№5
Г. Лермонтова
2012
Данная разработка по теме «Геометрический смысл производной»
состоит из двух разделов. В первом разделе рассмотрены подробные решения
простейших
примеров
и
задач,
предлагаемых
в
рамках
единого
государственного экзамена по выбранной тематике. Во втором разделе
приведены задания для самостоятельного решения различного уровня
сложности.
РАЗДЕЛ 1. ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
Прототип В8 первого типа.
Дан график касательной, необходимо
найти производную функции.
Решение задачи основано на геометрическом смысле производной и требует
нахождения углового коэффициента этой касательной, т.е. тангенса угла ее
наклона или отношение приращения функции к приращению аргумента на
удобном участке.
Задание 1.
На рисунке изображены график функции
точке с абсциссой
и касательная к нему в
. Найдите значение производной функции
в точке
.
Четко определены две точки с абсциссами -2 и 1 и ординатами
соответственно -4 и 2. Тогда y  
y2  y1 2  4

2
x2  x1 1  2
Ответ: 2.
Задание 2.
На рисунке изображены график функции
точке с абсциссой
и касательная к нему в
. Найдите значение производной функции
в точке
.
Задача решается так же, как и предыдущая. Только обратите внимание на
то, что угловой коэффициент касательной, а значит и производная должны
быть отрицательны.
Ответ: -2.
Задание 3.
На рисунке изображен график функции
. Прямая, проходящая
через начало координат, касается графика этой функции в точке с абсциссой 8.
Найдите значение производной функции в точке
.
Касательная не проведена, но обозначена точками. (0;0) и (8;10).
10:8 = 1,25
Ответ: 1,25.
Прототип задания B8 второго типа
Задание 1.
Прямая
является касательной к графику функции
.
Найдите a.
Здесь а является параметром, т.е. на самом деле задано семейство
функций одного вида. В этом семействе надо найти только одну,
удовлетворяющую условию задачи.
Прямая является касательной к графику функции, если выполняются 2
условия:
1. Производная функции равна угловому коэффициенту касательной. Но
при этом данная прямая и касательная могут оказаться параллельными.
Поэтому необходимо второе условие
2. Прямая и график функции пересекаются в предполагаемой точке
касания.
Найдем производную функции
угловому коэффициенту прямой:
y= ах² +2x+3 и приравняем ее к
2ах + 2 = 3; 2ах = 1.
Согласно второму условию 3х+1 = ах² +2x+3.
Получили систему двух уравнений с двумя переменными. Решая ее,
получим а = 0,125 и х = 4.
Ответ: 0,125.
Прототип задания B8 третьего типа
Задание 1.
Прямая
параллельна
функции
касательной
к
графику
. Найдите абсциссу точки касания.
Параллельные прямые имеют одинаковый угловой коэффициент. Найдем
производную функции и приравняем ее к угловому коэффициенту касательной:
Эта точка не является общей для графика функции и прямой, значит
прямая y=7x – 5 не совпадает с касательной.
Задание 2.
Прямая
функции
Найдем
является
касательной
к
графику
. Найдите абсциссу точки касания.
производную
функции
и
приравняем
ее
к
угловому
коэффициенту
Общей точкой является (проверяется подстановкой) только х = -1.
Прототип задания B8 четвертого типа
Задание 1.
На
рисунке
интервале
изображен
график функции
,
определенной
на
. Найдите количество точек, в которых касательная к
графику функции параллельна прямой
или совпадает с ней.
Прямая y=6 параллельна оси ОХ.
График данной функции имеет горизонтальную касательную в 4-х
точках:
Ответ: 4
РАЗДЕЛ 2. ЗАДАНИЯ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
1. Напишите уравнение касательной к графику функции y  f  x  в точке
графика с абсциссой x0 :
А) f  x   3x 2  x  1 , x0  1;
Б) f  x  
3x  1
, x0  1 ;
2x  1
В) f x   x  3 sin
x
 1 , x0  0 ;
3
4x  3
, x0  1.
3x  2
Г) f  x  
2. Напишите уравнения касательных к графику функции y  f  x  в
точках с ординатой y 0 :
А) y  x   x 2  4 x  11 , y0  7 ;
Б) y  x   x 2 , y0  4 ;
В) y  x  
3x  2
, y0  1 ;
5x  4
Г) y  x   tgx , y 0  0 .
3. Составьте уравнение касательной к линии y  sin x в точке с абсциссой
x0 

.
6
4. Найдите все общие точки графика функции y  f  x  и прямой
y  kx  b . В каких из этих точек данная прямая является касательной к графику
данной функции:
А) y  x   9 x 2  7 x  1, y 0   x ;
Б) y  x   x 3  3 x , y  2 ;
3
В) yx    x  3x , y  6 x  2 ;
Г) y  x 4  2 x 3  x 2  x , y  x ;
Д) y  cos x , y  1 ;
Е) y  sin x , y  x .
4. Напишите уравнения касательных к графику функции y  f  x  ,
параллельных данной прямой:
А) y  x   x 2  3x  1 , y  5x  11 ;
Б) y  x  
x2
, y  4 x  7 ;
x 1
Г) y  x  54 2 x  13 , y  0 ;
Д) y  x  sin 2 x , y  x .
5. На графике функции y  x 2  x  1 найдите абсциссу точки, в которой
касательная параллельна прямой y  3x  1.
6. На параболе y  x 2  7 x  3 найдите точку, касательная в которой
параллельна прямой 5 x  y  3  0 .
7. На графике функции
y  x 2 x  22 найдите точки, в которых
касательные перпендикулярны к оси ординат.
8. В каких точках линии y  x 3  x  2 касательная к ней параллельна
прямой y  2 x  1 .
9. Вычислите угол между касательными, проведенными к графику
функции y  f  x  в его точках с абсциссами x1 , x2 . Найдите общую точку этих
касательных:
А) y  x 2 , x1  2, x2  0 ;
Б) y  x 2  4 x  7 , x1  3, x2  1;
В) y 
Г) y 
1
x2
, x1  1, x2  1
3x  1
, x1  6, x2  0 .
x3
10. Найдите угол между касательными к графику функции y  x 3  x в
точках с абсциссами x1  1 и x2  1 .
11. На оси ОХ найдите такие точки, что две проведенные из них
касательные к графику функции y  f  x  образуют данный угол  :
А) f  x   x 2 ,   45 0 ;
Б) f  x   x 2  6 x  9 ,   arctg8 .
12. В каких точках касательная к графику функции y 
x2
образует с
x2
осью ОХ угол 135 0 ? В ответе записать сумму абсциссы и ординаты точки
касания при условии, что они больше 1.
13. На данной прямой найдите такую точку, что две касательные,
проведенные из нее к графику функции y  f  x  , взаимно перпендикулярны:
А) y  x 2  5 x  3 , y  x  6 ;
Б) y  0,25 x 4 , y  8 x  12 .
14. При каких значениях p данная прямая будет касательной к графику
данной функции:
А) y  3x 2  5 x  1 , y  2 x  p ;
Б) y  x 2  7 x , y   x  p ;
В) y  x 2  2 x , y  px  4 .
15. Найдите общие точки графиков двух данных функций и установите, в
каких из этих точек есть общие касательные к этим графикам:
А) y  x 3  2x 2 , y  x 2  5 x  3 ;
Б) y  x 4  x 3  3 x , y  x 3  x  3 .
16.
Имеют
ли
графики
данных
функций
общую
касательную,
проведенную через их общую точку:
А) y  5 x 2  2 x  3 , y  x 2  2 x  2 ;
Б) y  x 2  3x  20 , y   x 2  9 x  2 .
17. При каких значениях a данные параболы имеют общую точку, через
которую проходит их общая касательная:
А) y  x 2  4 x , y  2 x 2  a ;
Б) y  x 2  2ax , y  3x 2  1 .
18. Напишите уравнения всех касательных, проведенных из данной точки
к графику функции y  f  x  :
А) f  x   x 2 , M 0;4 ;
Б) f  x   x 2  2 x  1 , M 5;0 ;
В) f  x   3x 2 , M 0;2 ;
Г) f  x   x 3  3x  2 , M 1;0 .
19. Найдите уравнения общих касательных графиков данных функций:
А) y  x 2 , y  x 2  2 x ;
Б) y  x 2  3 x , y  x 2  x  1 ;
В) y  x 2  3x  7 , y   x 2  x  3 ;
Г) y   x 2 , y  x 2  4 .
20. Сколько касательных к графику функции y  x 3  3x проходит через
точки а) M  1;2 , б) N 2;2?
21. Найдите площадь фигуры, ограниченной графиком функции
y  x 2  4 x , осью ординат и касательной, проведенной к графику этой функции
в точке с абсциссой x0  5 .
22. Найдите площадь фигуры, ограниченной графиком функции
y  x 3  3x и касательной, проведенной к нему в точке с абсциссой x0  2 .