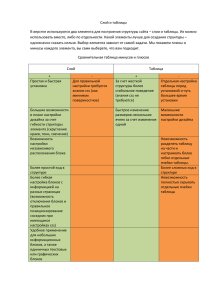
Методика синтеза помехоустойчивых детекторов границ

В работе описан метода синтеза помехоустойчивых детекторов краев, базирующихся на нейронных сетях, настраиваемых по методике «Обучение с учителем» с помощью одношаговой процедуры обучения. Предлагаемый метод синтеза помехоустойчивых детекторов краев и методология его использования универсальны по отношению к размерам и форме локальной области и достаточно легко обобщается на многослойные сети прямого распространения.
В качестве примера приводятся примеры синтеза ряда нейроноподобных детекторов границ с маской 5*5, реализованного на программируемой логики и его экспериментальной проверки при обработке реалтаймового видеопотока.
УДК 681.325.5
А. М. Астапкович (канд. техн. наук, доц.) – начальник СКБ ГУАП
С. А. Чернышев – магистрант кафедры вычислительных систем и сетей
МЕТОДИКА СИНТЕЗА ПОМЕХОУСТОЙЧИВЫХ ДЕТЕКТОРОВ ГРАНИЦ
В веден ие
Выделение границ изображений является ключевым элементов современных систем компьютерного зрения при решении ряда прикладных задач, связанных с распознаванием образов [1]. Границы представляют собой подмножество точек
исходного изображения, связанные с границами предметов или другими существенными элементами изображения.
Алгоритмы выделения границ и привязка их к существенным элементам изображения называют детекторами краев
(edge detector) [2]. Точки изображения, в которых яркость изменяется особенно сильно, называют краевыми точками, а их
совокупность формирует края областей изображения. Детекторы краев используют для анализа принадлежности рассматриваемой точки исходного изображения локальный фрагмент изображения, на основании анализа которого делается вывод о наличии краевой точки.
Как правило, детекторы краев дают большой выход при наличии резких локальных изменений яркости. Широкий
класс систем технического зрения эксплуатируется в условиях наличия шумов и помех. Шумы существенным образом искажают информацию о положении краевых точек, что приводит к появлению двух типов возможных ошибок. Первый тип связан с пропуском реально существующей краевой точки, а второй, с появлением ложной. Детектор краев CANNY считается
одним из лучших, но, как это следует из рис. 1, он не работоспособен при наличии шумов.
Улучшение качества детекторов краев требует увеличения площади фрагмента изображения, используемого для
принятия решения о наличии краевой точки, а также сложных алгоритмов обработки. С точки зрения реализации это означает необходимость выполнения большого объема вычислений. Естественно, что для видеосистем сложность реализации
помехоустойчивых фильтров границ существенно сложнее из-за необходимости обрабатывать 25 – 30 кадров в секунду.
Можно констатировать, что проблема разработки помехоустойчивых детекторов краев является актуальной, а способы ее решения во многом определяют параметры подсистем технического зрения. Как показывает анализ, решение задачи обработки видеоинформации невозможно без применения параллельных вычислений.
Одним из возможных вариантов реализации помехоустойчивых детекторов краев является использование методологии нейронных сетей. В этом направлении в настоящее время ведется интенсивная работа. Ряд результатов применения нейронных сетей для обработки изображений изложен в работах [1 – 3]. В работе излагается ряд результатов, связанных с разработкой метода синтеза помехоустойчивых детекторов краев, базирующихся на нейронных сетях, настраиваемых
по методике «Обучение с учителем» с помощью одношаговой процедуры обучения [4, 5]. Разработка методологии применения нейронных сетей в системах управления на протяжении ряда лет ведется в СКБ ГУАП. Настоящая работа содержит
изложение ряда результатов, связанных с применением этого подхода в системах обработки видеоинформации.
Предлагаемый метод синтеза помехоустойчивых детекторов краев и методология его использования универсальны
по отношению к размерам и форме локальной области и достаточно легко обобщается на многослойные сети прямого распространения.
a)
b)
c)
d)
Рис.1. Использование детектора краев CANNY для тестового изображения LENA
a – чистое изображение; с – зашумленное изображение b; d – обработанные изображения
Для экспериментов был синтезирован помехоустойчивый детектор границ с размерами локального фрагмента
5×5 пикселов. Синтезированные детекторы краев были реализованы на демонстрационной плате с чипом программируемой логики фирмы ALTERA.
Экспериментальное исследование для выделения границ показало высокую эффективность предлагаемого подхода, как в части реализации процедуры обучения, так и в части необходимых для реализации аппаратных ресурсов.
По результатам выполненной работы в заключении сформулированы перспективные направления дальнейших исследований с целью привлечения к этой области молодых ученых.
Ней роно под обн ы й д ете кт ор г ран иц
Предлагаемая структура фильтра ориентирована на использование в системах реального времени и предполагает
реализацию на параллельных вычислительных структурах.
Базовый компонент детектора, осуществляющий обработку изображения, представляет собой однослойный нейроноподобный детектор границ. Базовый цикл обработки изображения представлен на рис. 2.
Исходное изображение представляет собой матрицу значений яркости Is размером Ny×Nx. Результатом обработки
этой информации является матрица описания краев Ie обрабатываемого изображения также размером Ny×Nx. Для формирования значения элемента (i,j) матрицы краев используются N×N элемент матрицы исходного изображения, формирующих
маску фильтра границ. Из соображений симметрии маска фильтра квадратная, а N принимает нечетные значения.
Маска фильтра
границ
S1
S2
………
SN+1
S-векторное
представление маски
S2N
………
W-вектор Tmax /Tmin
весов
пороги
SN
SN*N
S1
S2
..
SNN
L =(W,S)
A
1
Is – МАТРИЦА
ИЗОБРАЖЕНИЯ
Ny×Nx
Ie – МАТРИЦА
КРАЕВ
Ny×Nx
i
i
j
j
Рис. 2. Обработка изображения однослойным нейроноподобным детектором границ
Таким образом, для принятия решения о принадлежности точки (i,j) к подмножеству краевых точек используется N×N
близлежащих элементов обрабатываемого изображения. Эти элементы упорядочиваются, и из них формируется вектор S
размерности Nsen=N×N+1, содержащий значения яркости в окрестности (i,j). Размерность вектора S на единицу больше,
чем количество используемых точек. Компонента N+1 вектора S имеет фиксированное значение 1, что обеспечивает возможность учета постоянной составляющей.
При обработке изображения вектор показаний сенсоров S подается на вход нейрона. Нейрон состоит из двух компонент: линейной (L) и нелинейной (A). Линейный компонент нейрона L имеет Nsen вход и использует для обработки вектор весов W размерностью Nsen. Линейная часть нейрона L выполняет скалярное умножение вектора S на вектор весов
W. Компоненты вектора W определяются на этапе синтеза. В терминах теории нейронных сетей эта процедура называется
обучением нейронной сети.
Нелинейная часть нейрона A представляет функцию специального вида [1, 2]. В рамках данной работы будут использоваться кусочно-линейные активационные функции. Универсальное описание кусочно-линейной активационной функции требует задания двух пар параметров (Tmin_in ,Tmin_out) и (Tmax_in, Tmax-out).
Активационная функция этого типа (рис. 3,a) описывается парой (Tmin ,Tmin) и (Tmax, Tmax). Для минимизации описания активационной функции такого вида будем использовать обозначение A(Tmax/Tmin). Функция (рис. 3,b) осуществляет
так называемую операцию бинаризации и описывается парами (Tmin ,0) и (Tmax,1). По аналогии для ее обозначения представляется естественным использовать обозначение B(Tmax/Tmin).
y(x)
y(x)
1
Tmax
Tmin
0
Tmin Tmax
x
x
Tmin Tmax
a)
b)
Рис. 3. Нелинейные компоненты нейрона
Нелинейный компонент нейрона может иметь сложную структуру, включающую в себя элемент, выполняющий последовательно несколько преобразований, описываемых линейно-кусочными преобразованиями разного типа.
Обработка изображения однослойным нейроноподобным фильтром границ со структурой, представленной на рис. 2,
состоит из Ny×Nx однотипных преобразований элементов исходного изображения. Для однослойных детекторов параметрами обработки являются: вектор весов W линейной части и параметры активационной функции нелинейной части. При
синтезе многослойных детекторов следует определить структуру связей между слоями. В простейшем варианте, она может
повторять структуру с рис. 2. В этом случае изображение, обработанное первым слоем детектора, подается на вход второго
слоя и т.д.
Предлагаемая структура фильтра идеально приспособлена для распараллеливания и в пределе обеспечивает возможность использования Ny×Nx нейроноподобных структур. В этом случае ее быстродействие будет максимальным, что,
однако, потребует запредельно большого количества аппаратных ресурсов. Минимального количества ресурсов потребует
последовательная поэлементная обработка матрицы описания исходного изображения.
С практической точки зрения интерес представляет комбинированный подход, базирующийся на параллельнопоследовательной реализации обработки. В этом случае реализуется нейронноподобная структура, состоящая из некоторого количества фильтров, параллельно осуществляющих описанное преобразование.
Об ща я с хе ма ме тод а
Синтез детектора подразумевает выбор структуры нейронной сети, выбор типов используемых активационных
функций, определение конкретных значений весов и порогов активационных функций.
Предлагаемый метод синтеза шумоустойчивых детекторов краев базируется на использовании нейросети прямого
распространения (персептрона) с кусочно-линейными активационными функциями. При этом сеть может иметь несколько
слоев нейронов.
Методологию синтеза нейроноподобного фильтра (обучения персептрона) рассмотрим на примере однослойной сети. Ее обучение содержит два ключевых этапа: определение весов и определение порогов активационной функции.
Наиболее популярный метод определения значений весов для персептрона является использование методики
«Обучение через показ». Применительно к рассматриваемой задаче это подразумевает использование набора обучающих
примеров, представляющих собой пары: матрица изображения – матрица краев. При этом могут использоваться как фрагментах одного изображения, так и несколько изображений. Для решения этой задачи представляется целесообразным использование одношаговой процедуры обучения, использование которой для ряда задач описано в работах [4, 5].
Общая схема применения этой процедуры не меняется, но ее применение для синтеза нейроноподобных алгоритмов обработки видеоизображений имеет ряд особенностей.
Рис.4. иллюстрирует процесс формирования исходной системы линейных уравнений, используемой для определения вектора весов W. Для этого требуется пара матриц (Is,Ie), представляющих собой обучающий пример. Для обозначения примеров в дальнейшем будем использовать обозначение L (от английского Lesson) c добавлением его порядкового
номера, например, L1, L2 и т.д.
С помощью матрицы изображений Is формируется матрица показаний сенсоров Ms. У этой матрицы количество
строк, равно количеству элементов матрицы описания исходного изображения или его фрагмента Ny×Nx. Количеством
столбцов N×N +1 зависит от размерности маски фильтра N и учитывает наличие постоянной составляющей. Порядок заполнения столбцов матрицы зависит от принятого способа упорядочения компонент матрицы фильтра. В дальнейшем изложении будет использована дисциплина упорядочивания, представленная на рис.2.
Для определения вектора весов W формируется вектор F, компоненты которого представляют собой желаемый результат работы детектора применительно к каждой конкретной точке исходного изображения. Этот вектор формируется из
матрицы Ie изображения краев. Его значения зависят от принятого способа представления краев изображения, т.е. от используемой методики обучения.
Таким образом, система линейных уравнений, определяющая вектор весов W нейродетектора, имеет вид
(1)
Размерность вектора W равна количеству столбцов в матрице Ms, а именно, Nsen. Матрица Ms прямоугольная и количество строк в ней зависит от количества элементов матрицы описания исходного изображения и матрицы описания
краев. Количество строк в ней существенно превышает количество столбцов, и соответственно, система (1) переопределена.
В этой ситуации задача определения вектора W формулируется в виде задачи минимизации евклидовой нормы
невязки
(2)
Обучающий пример
L= (Is,Ie)
Матрица значений сенсоров
Is – МАТРИЦА
ИЗОБРАЖЕНИЯ
Ny*Nx
Ms =
i
Ms11 Ms12
………
Ms1 Nsen-1 1
Ms21
Ms22
………
Ms2 Nsen -1 1
Msk1
Msk2
………
Msk Nsen -1 1
……
j
Вектор значений граничных точек
Ie- МАТРИЦА
КРАЕВ
Ny*Nx
F1
F2
F =
…
i
Fk
……
j
Рис. 4. Обработка обучающего примера
Универсальное решение, подразумевает необходимость использование регуляризации получающейся системы
…
уравнений [6, 7].
)
(3)
C математической точки зрения формулировка (3) означает устранение возможной сингулярности за счет поиска
решения с минимальной нормой вектора W за счет поиска согласованного минимума по W нормы невязки для системы
уравнений (1) и минимума нормы вектора W, который входит в результирующий функционал с весом γ, называемым регуляризирующим коэффициентом. Величина этого коэффициента для рассматриваемых приложений составляла 0.01 – 0.1.
Несколько забегая вперед, следует отметить, что с практической точки зрения, формулировка задачи обучения в
таком виде означает возможность использования одинаковых фрагментов изображений без риска получить вырожденную
систему уравнений.
С использованием скалярного произведения задача (3) записывается в виде
(4)
Решение задачи (4) представляет решение системы уравнений с квадратной матрицей размерности Nsen
(5),
где Ms’ представляет собой транспонированную матрицу S, E – единичная (квадратная) матрица размерности Nsen.
Соответственно, выражение для коэффициентов обученной по одной паре изображений нейронной сети выражается
в виде
(6)
Как следует из процедуры построения матрицы Ms и вектора F, возможно как разбиение исходного изображения на
фрагменты, так и использование нескольких пар обучающих примеров. В этом случае Ms и F представляют собой матрицу
и вектор, сформированные из матриц и векторов, соответствующих каждой паре обучающих примеров. Размерность матрицы линейных уравнений (5) от этого не увеличивается, но при этом соответствующим образом возрастает количество
строк в матрице Ms и, аналогично, размерность вектора F.
Представление (7) является иллюстрацией использования двух пар обучающих примеров L1 = (Is1, Ie1) и
L2=(Is2, Ie2) для формирования суммарной матрицы Ms и суммарного вектора F
Ms 
Ms1
Ms 2
(7)
Используя представление (7) рассмотрим особенности и перспективного подхода к обучению, связанный с последовательным использованием пар обучающих примеров.
Пусть нейронная сеть обучена с использованием примера L1, и в этом случае в соответствии с формулой (6) значение вектора весов будет равно
(8)
В случае использования двух пар обучающих образцов L1 и L2 с учетом представления (7) вектор весов в соответствии с формулой (6) записывается в виде
(9)
Представление (9) естественным образом обобщается на случай k обучающих пар. При этом возможно дальнейшее обобщение. Введем матрицу ME и вектор FE накопленного опыта, зависящий от количества примеров, использованных
для обучения
(10)
Представляется важным подчеркнуть, что размерность матрицы накопленного опыта будет равна Nsen×Nsen.
В этих обозначениях значение вектора весов при использовании k пар образцов для обучения принимает вид
(11)
(12)
С теоретической точки зрения это означает, что вся информация о (k-1) паре обучающих образцов сконцентрирована в матрице и векторе накопленного опыта. C практической точки зрения это означает, что при условии сохранения матрицы и вектора накопленного опыта, дообучение нейронной сети (нейрофильтра) может быть реализовано очень экономичным образом.
Син те з л ин е йн ой ча ст и
Стандартный подход к обучению нейронных сетей включает в себя выбор весов путем использования обучающих
примеров и оценки качества сети на тестовом изображении.
В качестве содержательного примера в дальнейшем изложении будет использован фильтр 5×5, соответственно
N=5, а количество коэффициентов линейной части фильтра составляет 26.
Для его обучения и тестирования использовались синтезированные изображения, представленные на рис 5 и
рис. 6, из которых формировались обучающие примеры L1 и L2.
Рис. 5. Обучающие примеры L1 и L2
а) исходное изображение; b) зашумленное изображение; с) края изображения
На рис 5 показаны использованные обучающие примеры L1 и L2, представляющие cобой искусственно сгенерированные изображения размерностью 100×100 (колонка a). Зашумленные изображения из колонки b получались путем наложения случайного шума заданной интенсивности на исходные изображения. Изображения краев из колонки с формировались путем обработки исходного изображения, алгоритмом, имитирующим формирования границы «вручную». Для этого в
исходном изображении оставлялись только краевые точки и отбрасывались остальные. При этом имелась возможность
управлять шириной формируемой границы – 1 или более элементов.
Размерность матриц Ms1 и Ms2 равна Nsam×Nsen. Количество строк Nsam зависит от размерности маски детектора N из-за необходимости учета особенностей граничных элементов. Для рассматриваемого случая N=5 величина Nsam
несколько меньше 10 000. Естественно, что вектора F1 и F2 будут иметь такую же размерность. Таким образом, для определения значения вектора W количество уравнений в (1.) было около 20 000.
В таблице 1 приведены параметры линейной части фильтров, обученные по образцам с рисунка 5. Идентификации
фильтров осуществляется следующим образом. Обозначение детектора H52 + A (255/30) означает, что для обучения использовался образец с ручным заданием границ с размерностью области N=5 и два обучающих примера L1 и L2. Активационная функция нелинейной части имела верхний порог 255 и нижний 30.
Таблица 1.
Линейная часть помехоустойчивого детектора краев
-0.0014
-0.069
0.137
-0.083
0.0042
0.0047
-0.045
0.03
-0.054
0.013
0.0064
-0.0435
0.0445
H51 – помехоустойчивый нейрофильтр краев
(маска 5*5 / обучение по образцу L1/ширина края 1)
-0.071
-0.073
0.134
-0.148
-0.143
0.09
0.091
0.094
0.371
-0.159
-0.164
0.076
-0.074
-0.066
0.151
Вес для 26 элемента
-1.543
H52 – помехоустойчивый нейродетектор краев
(маска 5*5 / обучение по образцам L1и L2/ширина края 1)
-0.046
-0.037
0.048
-0.112
-0.114
0.037
0.044
0.049
0.539
-0.12
-0.126
0.026
-0.038
-0.037
0.051
Вес для 26 элемента
-0.598
H52 – помехоустойчивый нейродетектор краев
(маска 5*5 / обучение по образцам L1и L2/ширина края 1)
-0.0435
-0.0435
0.0445
-0.1208
-0.1208
0.0382
0.0382
0.0382
0.5409
-0.0088
-0.071
0.145
-0.07
0.00037
0.0011
-0.046
0.039
-0.047
0.0055
0.0064
-0.0435
0.0445
-0.0435
0.0064
-0.1208
-0.0435
0.0382
0.0445
Вес для 26 элемента
-0.1208
-0.0435
-0.0435
0.0064
-0.598
Результаты тестирования однослойного нейрофильтра краев c использованием нейродетекторов H51 и H52 представлены на рис. 7 и 8. При этом использовалась активационная функция, представленная на рис. 3,а, для которой были
назначены пороги Tmax=255 и Tmin=30. Выбор значения верхнего порога 255 является естественным при использовании
яркостной компоненты для формирования изображения. Нижний порог на первом этапе выбирался путем визуального
сравнения качества фильтрации тестового изображения.
Следует отметить, что сравнение рис. 7,b и рис. 8,b демонстрирует эффект улучшения качества детектирования
краев, что выражается в наличии меньшего количества появления ложных границ на туловище собаки.
L1PP = 12.446
Рис. 6. Тестовое изображение
Выше была изложена общая схема синтеза нейроноподобных помехоустойчивых детекторов краев. Ее практическая
реализация требует введения нормы, позволяющей оценивать разницу между изображениями.
В теории защиты информации используется термин атака. Наложение шума на изображение следует трактовать, как
вариант атаки. Соответственно, наличие нормы, позволяющей оценивать разность между исходным и зашумленным изображением, позволяет количественно оценить «свирепость» атаки. Качество обучения и качество синтезированного фильтра
с помощью такой нормы оцениваются, как разность изображений краев, использованных при обучении, и изображений краев, получаемых с помощью синтезированного нейродетектора.
Как показал выполненный анализ, для этого хорошо подходит классическая норма L1, приведенная к одному элементу изображения
(13)
В таком варианте норма представляет собой средний уровень разницы для одного пиксела изображения, что отображается в обозначении этой нормы, являющейся сокращением L1 Per Pixel. На рис. 5 и рис.6 приведена оценка свирепости атаки, выполненная с помощью этой нормы.
a) H51 + A (255/30)
b) H51 + A (255/30)
Рис. 7 Детектирование краев чистого a) и зашумленного b) изображения однослойным нейродетектором H51 (инвертированное изображение)
a) H52 + A (255/30)
b) H52 + A (255/30)
Рис. 8. Детектирование краев чистого a) и зашумленного b) тестового изображения однослойным нейродетектором H52 (инвертированное изображение)
Вы бор по рог ов ак ти ва ци о н н ой фун к ц ии
Для фильтра краев изображений, использующих яркостную компоненту, естественным является выбор для максимального порога максимально возможного значения 255.
Анализ графика L1PP, как функции от нижнего порога, позволяет рациональным образом выбирать нижний порог.
Для каждой точки графика требуется обработать зашумленное изображение синтезируемым фильтром с задаваемыми
порогами и рассчитать для него норму L1PP по отношению к изображению краев, использованному при обучении. На рис. 9
приведены результаты оценки качества фильтрации с помощью нормы L1PP, как функции от значения нижнего порога активационной функции.
10
8
RF1k
RF2k
6
4
2
0
20
40
Tmk
60
80
Рис. 9. Оценка качества фильтрации с помощью нормы L1PP
Зашумленные изображения прямоугольников из обучающего примера S1 обрабатывались с помощью фильтров H51
(кривая RF1) и фильтра H52 (кривая RF2) с разными нижними порогами. На рис 5. представлены графики L1PP (Tmin) для
этих изображений и изображения краев прямоугольников, использованных при обучении линейной части детектора.
Анализ этих данных позволяет сделать ряд практически значимых выводов. Значение нижнего порога активационной функции существенным образом влияет на качество детектора краев. Эти графики имеют плато для значения L1PP ≈ 3
в диапазоне значений нижнего порога 30 – 50. При этом детектор краев H52, обученный с помощью примеров L1 и L2 при
обработке зашумленного изображения из примера L1 дает в этом интервале несколько худшие значение, чем детектор,
обученный только с помощью примера L1. В интервале 30 – 40 оба детектора обеспечивают приблизительно одинаковое
качество.
Следует, однако, обратить внимание, что использование нормы L1PP, не отменяет необходимости визуального анализа качества детектора с использованием тестового изображения.
Как следует из рис. 9, значения L1PP для значений нижнего порога 30 – 40 – 50 активационной функции отличаются
незначительно. С другой стороны, как это следует из рис. 8 и рис 6, детектор H52+A(255/50) работает значительно хуже по
сравнению с детекторами H52+A(255/30) и H52+A(255/40). В частности его применение приводит к существенному увеличению ошибок, связанных с пропуском реально существующих краевых точек, вплоть до пропуска существенных фрагментов. Например, на изображении с рис 10,b у собаки отсутствует глаз.
Для удобства восприятия, приведенные изображения инвертированы. Для этого матрица яркости пересчитывается
Iinv(i,j) = 255-Iorg (I,j).
а) H52 + A (255/40)
b) H52 + A (255/50)
Рис. 10. Детектирование краев зашумленного тестового изображения однослойным нейродетектором H52 (инвертированные изображения)
Улучшение качества детектора может потребовать введение дополнительных слоев. Представляется важным подчеркнуть, что с этой точки зрения предлагаемый метод синтеза универсален и применяется аналогичным образом к выбору параметров второго слоя.
Для синтеза может быть использован обучающий пример, состоящий из изображения краев, являющегося результатом обработки однослойным детектором краев, и изображением краев из обучающего примера, использованного на первом
этапе.
Возможен и более радикальный подход к использованию полученных на первом этапе результатов. В качестве обучающего примера для второго слоя можно использовать пару, состоящую из зашумленного тестового изображения и изображения краев, получаемые посредством применения однослойного детектора к чистому тестовому изображению. В качестве иллюстрации укажем, что может быть использована пара с рис. 7,a и с рис. 6,b.
Си мме тр и чн ы е де тек то р ы кра ев
Предлагаемый подход обучению линейной компоненты нейрона имеет универсальный характер. Этот подход использовался в численных экспериментах с виртуальным мобильным роботом SOFA-2009 [6]. Эти эксперименты позволили
обнаружить наличие эффекта асимметрии обучения нейронных сетей, описанного в работе [7].
Применительно к задаче синтеза детектора краев с локальной зоной, имеющей форму квадрата, естественным требованием является обеспечение симметрии коэффициентов, под которым понимается равенство весов для сенсоров,
расположенных симметрично относительно осей квадрата. Это требование обеспечивает эквивалентность процедуры обработки одного и того же изображения при его повороте.
С точки зрения реализации для обработки показаний сенсоров, формирующих соответствующие симметричные
подмножества, их значения следует просуммировать, и далее умножить на соответствующий вес. Соответственно, сенсоры детектора такого типа будут иметь сложную структуру. Их использование приводит к радикальному уменьшение числа
свободных параметров, которое можно использовать при синтезе детектора.
Рис. 11 иллюстрирует вариант формирования сенсоров детектора, обеспечивающего симметрию для квадратной
локальной зоны с размерностью 5×5. На этом рисунке приведена дисциплина упорядочения пикселов исходной локальной
зоны и их сборка в группы для сенсоров симметричного детектора. В несимметричном варианте детектор краев имеет 26
свободных параметров (5×5+1), в симметричном варианте это число уменьшается до 7 (6+1).
Для синтеза детектора краев с составными сенсорами процедура синтеза (обучения) линейной части, описанная
выше, не требует модификации. Естественно, что при этом меняется размерность (количество столбцов равно 7) и схема
формирования матрицы фильтра границ S с рис. 2.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
Ss1 =S1+S5+S21+S25
Ss2 =S2+S4+S10+S20+S24+S22+S16+S6
Ss3 =S3+S15+S23+S11
Ss4 =S7+S9+S19+S17
Ss5 = S8+S14+S18+S12
Ss6 = S13
Рис. 11. Структура сенсоров симметричного детектора 5×5
В работе [6] предложен метод определения коэффициентов (вектора весов W) c помощью одношаговой процедуры обучении решений обладающих свойствами симметрии. В основе этого метода лежит метод множителей Лагранжа и
явно учитывается линейный характер соотношений между весами.
Кратко рассмотрим этот способ применительно к задаче синтеза фильтра краев.
Коэффициенты симметричного нейродетектора должны удовлетворять соотношениям, представленным на рис. 5.1.
Например, первая строка дает три уравнения связей: S1=S5, S1=S21, S1=S25.
Эти соотношения между коэффициентами записываются в виде
(14)
Матрица L прямоугольная и для рассматриваемого случая детектора краев с маской 5×5 будет иметь 19 строк (по
числу соотношений между коэффициентами) и 26 столбцов (о числу коэффициентов). Метод множителей Лагранжа применительно к рассматриваемой задаче представляет поиск минимума функции R по компонентам вектора W и вектора, образованного множителями Лагранжа
,
(15)
где Dµ – диагональная матрица с коэффициентами µi на диагонали.
Размерность квадратной матрицы Dµ определяется количеством наложенных соотношений на веса W. Диагональные элементы Dµ образуют вектор множителей Лагранжа µ.
Для нахождения решения, удовлетворяющего системе линейных соотношений (14) ищется минимум функции F(W,µ)
по компонентам векторов W и µ. Для этого градиент функции F(W,µ) приравнивается нулю. Если ввести вектор Wµ, образованный объединением векторов W и µ, и вектор Fµ, образованный из вектора F, дополненного количеством нулей, равным количеству уравнений в (14), то решение (15) применительно к этим векторам записывается в виде, аналогичном 8).
W

 S  1 S  
F
0
(16)
При этом матрица этой расширенной системы имеет вид
Ms 
MsMs   E T 
T
0
(17)
В таблице 1 приведены коэффициенты симметричного детектора краев, полученные с помощью этого способа.
Следует указать, что асимметричность линейной части детектора может служить оценкой качества набора обучающих примеров. Из этого следует необходимость иметь в арсенале разработчика набор подходов, обеспечивающих синтез
как симметричных, так и несимметричных детекторов.
Ап пар атн ая реа ли за ция д ете кто ра кра ев
Предлагаемая методика синтеза изначально была ориентирована на реализацию на чипах программируемой логикой, так как этот тип элементной базы обеспечивает реальное распараллеливание обработки видеоизображений.
Синтез детекторов был реализован с помощью пакета MathCad 14. Параметры экспериментально исследованных
детекторов приведены в таблице 1. Детекторы аппаратно реализовывались на демонстрационной плате «University Development and Education Boards Altera DE2-115» с чипом программируемой логики Cyclone EP4CE115.
На рис. 6.1 представлен стенд для изучения свойств помехоустойчивого однослойного детектора краев. Источником
сигнала служила видеокамера SONY, подключенная к видеовходу платы DE2-115. Видео поток с камеры обрабатывался в
реальном времени. Для каждого выделяемого кадра производилось выделение краев. Для отображения полученной информации использовался VGA монитор ПК.
Проведенные эксперименты подтвердили хорошее качество выделения краев с помощью детекторов синтезированных с помощью предлагаемого метода. При этом следует отметить, что была использован однослойный детектор краев,
синтезированный с использованием искусственно сгенерированных изображений
Рис. 12. Аппаратная реализация нейроноподобного детектора краев
Закл ю чен ие
Приведенные результаты позволяют сделать вывод об эффективности предлагаемого подхода, связанные, в
первую очередь, с его универсальностью и эффективностью при аппаратной реализации средствами программируемой
логики.
Кратко рассмотрим перспективные направления развития предлагаемого подхода применительно к методам синтеза
нейродетекторов краев.
Во-первых, результаты обработки синтезированным нейродетектором исходного и зашумленного изображения могут быть использованы для его переобучения. Например, пара изображений 6,b и 7,a или 8,a могут быть использованы, как
пример L1. Эта же пара может быть использована для дообучения в виде нового примера L3.
Во-вторых, эта же пара или пары, образованные путем фильтрации зашумленных изображений 5,b и изображений
5,с могут быть использованы для обучения второго слоя нейродетектора. Для этих же целей могут быть использованы и
пара L3.По сути дела этот подход обеспечивает возможность синтеза многослойных нейродетекторов.
В-третьих, для генерации обучающих примеров возможно использование реальных изображений с искусственно
нанесенным шумом и этих же чистых изображений, обработанных эвристическими алгоритмами выделения краев, например, детектором CANNY. Представляется целесообразным особо выделить это направление исследований, назвав его
«Задачей копирования эвристик».
Авторы выражают искреннюю признательность Акатову А. за ряд замечаний, позволивших существенно улучшить
форму представления полученных результатов.
Библиографический список
1.
Лукьяница А.А., Шишкин А.Г. Цифровая обработка изображений. – М.: “Ай-Эс-Эс”, 2009. - 518с.
2.
Форсайт, Понс. Компьютерное зрение. Современный подход.: Пер. c англ. – М.: Издательский дом "Вильямс”, 2004.-928с.
3.
Хайкин С. Нейронные сети: полный курс, 2-е изд., испр.: Пер. с англ.- М.: ООО “И.Д. Вильямс”, 2006. - 1104 с.
4.
Astapkovich A. M. One step learning procedure for neural net control system. In proc. International forum “Information systems. Problems, perspectives, innovation approaches”, Vol. 2, p.3-9., SUAI, Saint-Petersburg, Russia, 2007.
5.
Astapkovich A. M . Virtual mobile robot SOFA-2009 for computational robotics research In proc. International forum “Information and communication technologies and higher education – priorities of modern society development”, p. 7-15, SUAI, Saint-Petersburg, Russia, 2009.
6.
Astapkovitch A.M. Learning Asymmetry Effect for the Neuron Net Control Systems. Proc. International forum “Modern information society formation – problems, perspectives, innovation approaches”, p.7-13, SUAI Saint-Petersburg, Russia, 2010.
7.
Тихонов А.Н.б Арсенюк В.Я. Методы решения некорректных задач - М.:Наука, Главная редакция физико-математической литературы, 1979, изд. 2-е,
с. 286.
8.
Бояринцев Ю.Е. Регулярные и сингулярные системы обыкновенных дифференциальных уравнений. Новосибирск: Наука, 1980, изд. 2-е, с. 223.