Баранова Олеся Васильевна
Baranova Olesya Vasilevna
Яицкова Анастасия Романовна
Iaitskova Anastasia Romanovna
Студенты
Students
Саратовский социально-экономический институт (филиал) РЭУ им. Г. В. Плеханова
Saratov Social and Economic Institute, (branch) GV Plekhanov
ПРИМЕНЕНИЕ МАТЕМАТИЧЕСКИХ МЕТОДОВ В ЛОГИСТИКЕ
APPLICATION OF MATHEMATICAL METHODS IN LOGISTICS
Аннотация на русском языке: Актуальность выбранной темы статьи связана с
растущей ролью логистики в сфере бизнеса и торговли, как на национальном, так и на
международном уровнях. При этом важно отметить, что логистика в прикладном своём
значении неразрывно связана с математической наукой, поскольку использует
математические методы с целью решения многих задач, таких как: принятие
краткосрочных решений, создание логических моделей реальных процессов логистики,
решение задач расчёта оптимального размера заказа, определение спроса на товар и так
далее. В данной статье мы проанализируем наиболее важные аспекты логистики в их
взаимосвязи с математической наукой, а также на практическом примере рассмотрим
применимость математических методов в решении задач логистики.
The summary in English: The relevance of the topic, which we have chosen is connected
with an increased role of logistic in the field of business and trading not only on the national
level, but also in the international relations. It is important to notice that the logistic in practical
use is connected with Mathematics, because it uses mathematical methods to solve such
problems as making short-term decisions, creating logical models of real processes in logistic,
solving the problems of calculating the optimal size of the order, determining the demand for
goods and so on. In this article we analyze the most important aspects of logistic with its
connections with Mathematics in addition on the practical example we consider the applicability
of mathematical methods in solving logistics problems.
Ключевые слова: логистика, математика, методы, математические методы в
логистике, задача, решение, расчёт показателей логистики.
Key words: logistic, Mathematics, methods, mathematical methods in logistic, a task, the
solution, calculation of logistics indicators.
Логистика – это наука, которая занимается планированием и
непосредственной
организацией
информационных потоков
перемещения
материальных
и
от первоначального источника до конечного
потребителя. Таким образом, можно сделать вывод о том, что логистика
выступает связующим звеном в области построения деловых отношений. В
современном мире, когда экономическая интеграция различных субъектов
достигла, фактически, своего пика, грамотное распределение ресурсов и их
Международный научный журнал «Синергия наук»
организация чрезвычайно важны, этим и объясняется важность самой науки
логистики, и специалистов, способных использовать её методы.
Методология любой науки, прежде всего, связана с системой задач и
целей, выполняемых данной наукой. Прежде чем обратиться к методам,
используемым логистикой, предлагаем рассмотреть основные задачи данной
науки. Итак, среди всего множества функций – задач, на решение которых
направлена
деятельность
науки
логистики,
принято
выделять
три
самостоятельные, но тесно взаимосвязанные группы: базисные, ключевые и
поддерживающие логистические функции.
К базисным функциям логистики относятся: снабжение (то есть
подготовка и организация сырья и других ресурсов в производстве продукта),
производство и сбыт конечного товара.
Ключевые
функции
включают
в
себя
управление
запросами
потребителей, транспортировка конечного продукта, управление закупками
и запасами, ценообразование, поддержание стандартов обслуживания
потребителей и другие.
Поддерживающие
функции:
складирование,
грузопереработка,
защитная упаковка конечного продукта, обеспечение возврата товаров, сбор
возвратных отходов, информационно-компьютерная поддержка, сервисное
обслуживание.
Логистика, по своей сущности, связана со многими науками, такими
как экономика, технология, техника и математика. Для осуществления
вышеизложенных функций логистами используются различные методы,
среди которых особое место занимают методы элементарной математики,
математической статистики и теории вероятностей.
Обосновывая ресурсные потребности, составляя отчёт затрат на
производство,
составляя
стратегию
работы
предприятия,
выполняя
балансовые расчёты, логисты обычно используют методы элементарной
математики. Следует отметить, что данные методы используются не только
Международный научный журнал «Синергия наук»
по отдельности, но и в сочетании с другими методами (например, в
сочетании
с
математического
изменения
методами
математической
программирования).
экономических
статистики,
Например,
показателей
может
методами
факторный
быть
анализ
осуществлен
с
использованием операций дифференцирования и интегрирования.
Ещё одной группой методов, широко используемых в экономическом
анализе, является группа методов математической статистики и теории
вероятностей. Как правило, применение данных методов имеет место в
ситуациях, когда анализируемые показатели могут быть представлены как
случайный процесс. Если связь между исследуемыми явлениями не
детерминированная, а стохастическая, то статистические и вероятностные
методы являются практически единственными инструментами исследования.
Наиболее используемым математически-статистическим методом логистики
является метод множественного и корреляционного анализа.
Для
применимы
исследования
одномерных
вариационные
ряды,
статистических
законы
совокупностей
распределения,
а
так
же
выборочный метод. Для многомерных статистических совокупностей
используются корреляции, регрессии, а так же дисперсионный и факторный
анализ.
Эконометрические методы, которые так же широко применяются в
логистике, основаны на единстве трёх наук: экономики, математики и
статистики. Здесь наиболее распространённым считается метод анализа
«затраты-выпуск», который представляет собой матричные (балансовые)
модели, которые строятся по схеме шахмат и позволяют наиболее
комплексно представить взаимосвязь данных экономических показателей.
Чем же удобны матричные модели? Прежде всего, это удобство расчётов и
понятность,
что
чрезвычайно
автоматизированной
обработки
важно
в
данных,
процессе
при
создания
построении
производства продукции.
Международный научный журнал «Синергия наук»
систем
стратегии
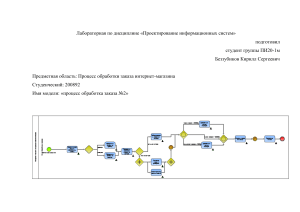
Более детально рассмотрим применение совокупности математических
методов в практической деятельности предприятия.
Рассмотрим бизнес-
процесс, связанный с деятельностью розничного предприятия, структура
работы которого, следующая:
1 этап. Формирование заказа на покупку, на основе анализа спроса на
рынке.
2 этап. Транспортировка готового продукта на склад.
3 этап. Оприходование и приём продукта на складе.
4 этап. Сортировка транспортированного на склад продукта.
5 этап. Поступление товара в сборку заказа для продажи.
6 этап. Подготовка продукта к транспортировке потребителю.
7 этап. Транспортировка заказа.
8 этап. Непосредственная доставка покупателя.
В ходе указанных выше этапов работы предприятия выполняются
соответствующие операции, математические расчёты с использованием
формул.
Первым шагом является анализ спроса на товар, который при заданных
данных ( n – некоторый товар, i – количество товара, а t-St – анализируемый
период времени). Основной задачей выступает создание прогноза на спрос
данной продукции в следующие 2-6 месяцев. Расчёт осуществляется при
помощи следующей формулы:
′
′
′
′
𝐷𝑖+1
= 𝑆𝑡+1
− 𝑆𝑡′ + 𝑄𝑡′ = ∆𝑆𝑡+1
+ 𝑄𝑡−1
,
′
где 𝑄𝑡−1
- объем заказа i-го товара в анализируемом периоде «t-1».
Однако, возвращаясь к условию того, что заказ на доставку товара в текущей
′
период “t” был сделан в предыдущем периоде, получим, что ∆𝑆𝑡+1
( спрос на
данный продукт в будущие месяцы), рассчитывается как разность уровней
временного ряда, значение которых в общем виде можно записать так:
𝑆 ′ (𝑡) = 𝑓 (𝑇, 𝑊, 𝐶, 𝜀),
Международный научный журнал «Синергия наук»
где T – трендовая компонента, W – сезонная компонента, C –
циклическая компонента, ε – случайное отклонение.
Однако, с целью
увеличения точности прогнозирования, нужно учесть фактор количества
точек сбыта, который должен оставаться. Чтобы рассмотреть аналогичный
показатель спроса, но при условии учёта количества точек сбыта данного
товара, воспользуемся дополнительными показателями:
K – количество точек сбыта в период времени t;
𝜌𝑖𝑘 - плотность населения в прилегающей к точке сбыта зоны - l метра;
𝜏𝑡𝑘 - часы работы точки сбыта «k» в период «t»;
и получим следующий прогноз спроса на данный товар в последующие
2-6 месяцев для фирм розничной сети:
𝐾 −𝐾𝑡−1
𝑆 ′ (𝑡) = [𝑓 (𝑇, 𝑊, 𝐶, 𝜀) + 𝑆 , (𝑡 − 1) ∗ 𝑡
𝐾𝑡−1
̅̅̅
𝜌
𝑡
] ∗ ̅̅̅̅̅̅̅
,
𝜌𝑡−1
где 𝐾𝑡 и 𝐾𝑡−1 – количество точек сбыта в текущий и предыдущий
периоды времени («t» и «t – 1» соответственно), а 𝜌̅𝑡 и ̅̅̅̅̅̅
𝜌𝑡−1 – средняя
плотность населения в обслуживаемых точками продаж областях.
2 шаг. Решение задачи оптимального запаса, то есть расчёт переменной
величины – количества хранимых запасов на складе предприятия в наиболее
эффективных
и
рациональных
для
предприятия
условиях.
Количество запасов на складе, с теоретической точки зрения, может
варьироваться в пределах от 0 до полной загрузки склада (назовём V), однако
каждый склад имеет определённый «страховой запас», который принято
обозначать как
𝐾стр. Таким образом, можно сделать вывод о том, что
объёмов хранимых на складе предприятия запасов зависит от двух основных
факторов:
1.
Потоков груза на склад (OF);
2.
Потоков грузов со склада (D), пользуясь которыми, мы сможем
разрешить поставленную задачу и рассчитать объём оптимального запаса:
Международный научный журнал «Синергия наук»
′
′
′
𝑆𝑡+1
= 𝑆𝑡′ + 𝑂𝐹𝑡+1
− 𝐷𝑡+1
- формула решения задачи оптимального
′
запаса, где 𝑆𝑡+1
и 𝑆𝑡′ – объемы запасов товара «i» на складе в текущем и
′
последующих временных периодах «t» и «t + 1», 𝐷𝑡+1
– поток грузов со
склада на магазины, который принимается равным спросу из-за наличия
страхового запаса.
Фактический объем товара «i», приходящего в период «t» –
′
𝑂𝐹𝑡+1
является стохастической величиной и зависит от объема заказа:
′
′
𝑂𝐹𝑡+1
= 𝑃 ∗ 𝑄𝑡+1
.
Важно
обозначение
следующего
условия:
страховой
запас,
представленный в следующей формуле, должен быть не меньше разности
между максимальной величиной спроса и минимальным объемом заказа:
𝐾 ′ = max{𝐷 ′ } − min{𝑂𝐹′ },
t – срок хранения грузов на складе;
T – время работы склада;
𝑇
h – оборачиваемость грузов на складе (ℎ = )
𝑡
V – вместимость склада.
3
метод.
Немаловажной
функцией
менеджера-логиста
на
предприятии является расчёт и последующий анализ оптимального размера
заказа, частота его осуществления. Через задачу поиска экономического
размера заказа Economic Order Quantity – EOQ можно получить ответ. В
традиционной модели общий объем годовых затрат 𝐶𝑟 равен
𝐷
𝑞
𝑞
2
𝐶𝑟 = 𝐶𝑟 (𝑞) = 𝐶0 + 𝐶𝑘 + 𝐶𝑘 𝐷.
Для максимизации q берется следующая производная
𝑑𝐶𝑟
𝑑𝑞
= 0.
Международный научный журнал «Синергия наук»
В результате решения получим формулу Харриса – Уилсона.
2𝐶0𝐷
𝑞∗ = √
𝐶ℎ
где 𝐶0 – накладные расходы на каждую поставку;
D – годовое потребление продукции;
𝐶ℎ – затраты на хранение единицы продукции в год.
С учетом поправок на неопределенность и процессы естественной
убыли рассчитываются следующим образом
𝑃𝑟 = 𝛼 [𝐶𝑟 − 𝐶𝑟 (𝜀𝑛 + ∆𝜀
𝑞
2𝐷
𝐷
𝑞
𝑞
2
)] 𝐷 − (𝐶0 + 𝐶𝑘 + 𝐶𝑛 𝐷).
При этом оптимальный размер заказа находится по следующей
формуле:
𝑞∗(𝐶𝑟(𝑚𝑜𝑑) ) = √
2𝐶0 𝐷
𝐶ℎ +𝛼𝐶𝑟 ∆𝜀
.
В то же время при условии наличия статистических данных с точки
зрения спроса задачу нельзя классифицировать как задачу в условиях
неопределенности. И, подставляя прогнозное значение величины спроса в
условие задачи, получим следующее выражение для оптимального объема
заказа, представленное в формуле:
𝑞∗(𝐶𝑟(𝑚𝑜𝑑) ) = √
2𝐶0 𝑓(𝑇,𝑊,𝐶,𝜀)
𝐶ℎ +𝛼𝐶𝑟 ∆𝜀
.
Периодичность заказа при этом исходя из классической задачи
определяется остатками товара на складах.
4. Задача формирования плана перевозок от группы поставщиков
группе покупателей. Поставщиками являются склады предприятия, а
потребителями – магазины. Критерий транспортной задачи следующий:
𝑐11𝑥11 + ⋯ + 𝑐𝑦 𝑥𝑔 → 𝑚𝑖𝑛,
𝑛
∑𝑚
𝑖=1 ∑𝑗=1 𝑐𝑦 𝑥𝑦 → 𝑚𝑖𝑛 ,
Где i = 1, 2,…, m, а j = 1, 2,…, n.
Международный научный журнал «Синергия наук»
Ограничения могут быть представлены системой:
𝑥𝑖1 + 𝑥𝑖2 + ⋯ + 𝑥𝑖𝑗 = 𝑎𝑖 или ∑𝑚
𝑗=1 𝑥𝑖𝑗 = 𝑎𝑖
{
.
𝑥1𝑗 + 𝑥1𝑗 + ⋯ + 𝑥𝑖𝑗 = 𝑏𝑗 или ∑𝑛𝑖=1 𝑥𝑖𝑗 = 𝑏𝑗
Кроме того, при решении классической задачи о назначениях
накладывается условие, что одну перевозку может совершать одно
транспортное средство. Эти условия имеют вид:
∑𝑛𝑖=1 𝑥𝑖𝑗 = ∑𝑛𝑗=1 𝑥𝑖𝑗 = 1.
Конечно,
охватить
все
функциональные
задачи
логистики
и
математические методы по их решению невозможно, однако, в нашей статье
были представлены основные задачи предприятия и математические методы
их решения: как прогнозировать спрос, рассчитать оптимальный объём
запасов, оптимальный объём заказа, а так же решение задачи по
формированию плана перевозок. Сейчас предлагаем вам на практическом
примере рассмотреть применение 3 метода и решить следующую задачу:
Условие задачи: в логистическую фирму “LogisticPlus2” обратилась
зарубежная компания по производству комплектующих для автомобилей
«MM» с вопросом: где заказ комплектующих будет наиболее оптимальным: в
Европе или в Юго-Восточной Азии? Исходные данные для решения задачи
представлены в Таблице №1 «Исходные данные»).
Таблица 1. Исходные данные
Стоимость товара
210
15
2
В ЮгоВосточной
Азии
(Са ),$
2000
В Европе
(Се ),$
Пошлина на импорт
товара из Европы
(ПИ ), %
(ЗС )
Транспортный
тариф
(ТТ ), $/м3
Страховые
Удельная
стоимость
поставляемого
товара
(У), $/м3
В пути (ЗП )
Ставка на
запасы,%
0.5
244
120
Рассчитав оптимальный размер заказа, ответьте на вопрос зарубежной
компании.
Международный научный журнал «Синергия наук»
Решение:
Первым шагом на пути к решению поставленной задачи станет расчет
доли
дополнительных
затрат,
которые
могут
возникнуть
при
транспортировке необходимых комплектующих из Юго-Восточной Азии.
Воспользуемся следующей математической формулой:
Д = 100 ∗
ТТ
+ ПИ + ЗП + ЗС (%)
У
Подставив исходные данные в формулу, получим следующее:
Д = 100 ∗
210
2000
+ 15 + 2 + 0,5 = 28%
-
процентное
соотношение
дополнительных затрат, возможных при транспортировке комплектующих от
поставщика из Юго-Восточной Азии.
Затем необходимо определить разницу между стоимостью комплектующих
Юго-Восточной Азии и в Европе. Предварительно обусловимся, что
стоимость импортируемого товара в
Европе равна 100%. Воспользуемся
формулой:
РС = (Се − Са ) ∗
100
, (%)
Са
РС = (244 − 120) ∗
100
= 103,3%
120
Финальным этапом решения нашей задачи будет
сравнение
показателя рассчитанного нами на первом этапе и на предпоследнем ( Д и
РС - соответственно). РС >Д, следовательно, наиболее оптимальным заказом
комплектующих будет заказ их в Европе.
Ответ: выгоднее закупать комплектующие в Европе.
Таким образом, можно сделать вывод о том, что вклад математики в
развитие логистики и прикладное её использование – огромен, в нашей
статье мы рассмотрели лишь некоторые элементарные методы решения
логистических задач с помощью построения математических моделей и
Международный научный журнал «Синергия наук»
составления формул, наилучшим образом иллюстрирующих взаимосвязь
этих двух, важных для современного общества наук.
Литература:
1.
анализа
Высочанская Е.Ю., Малышева Л.В.- «Применение факторного
при
анализе
сборнике: Современные
волатильности
инновационные
процентных
технологии
и
ставок//В
проблемы
устойчивого развития общества».- Материалы X международной научнопрактической
конференции.
Сборник
научных
статей
участников
конференции.- 2017.- С. 32-34.
2.
Савенкова Т.И.- «Логистика: учебное пособие для студентов,
обучающихся по специальностям «Финансы и кредит», «Бухгалтерский учёт,
анализ и аудит». – 5-е изд., стер. – М.: издательство «Омега-Л»,2010.
3.
Ольшевская Н. – «Экономический анализ. Шпаргалки». - ISBN
(EAN): 9785170616169. – 2009.
4.
Левкин Г.Г. – «Основы логистики». - ISBN: 978-5-9729-0070-1.,
изд.: «Инфа-инженерия», 2014.
5.
Малышева Л.В.- «Использование информационных технологий
при обработке результатов научных экспериментов» // В сборнике:
«Современные проблемы и тенденции развития внутренней и внешней
торговли».- 2013. - С. 246-251.
6.
[Электронный
ресурс]
статья:
«Задачи
логистической
эффективности розничной сети: модели и математические методы решения».
(автор:
Собко
Э.О.).
Режим
доступа:https://www.fundamental-
research.ru/ru/article/view?id=40995
Международный научный журнал «Синергия наук»