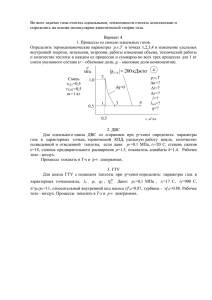
Теоретические основы теплотехники. Лекции. Горожанкин С.А., Дегтярёв В.И.

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ УКРАИНЫ
ДОНБАССКАЯ ГОСУДАРСТВЕННАЯ АКАДЕМИЯ СТРОИТЕЛЬСТВА И
АРХИТЕКТУРЫ
ДОЦЕНТ
ГОРОЖАНКИН С. А.
ПРОФЕССОР
ДЕГТЯРЕВ В. И.
ТЕОРЕТИЧЕСКИЕ ОСНОВЫ
ТЕПЛОТЕХНИКИ
КОНСПЕКТ ЛЕКЦИЙ
( ДЛЯ СПЕЦИАЛЬНОСТИ 7.090258 "АВТОМОБИЛИ И АВТОМОБИЛЬНОЕ ХОЗЯЙСТВО")
О Д О Б Р Е Н О:
Кафедрой "Автомобили и автомобильное хозяйство"
Протокол № от 27.04.2001г.
Советом
механического
факультета
Протокол №3 от 10.03.2001г.
МАКЕЕВКА
2001 г.
УДК 536.7 (075.8)
ГОРОЖАНКИН С. А., ДЕГТЯРЕВ В. И.
теплотехники (курс лекций). Макеевка: Донбасская
строительства и архитектуры, - 2001. - 110 с.: 76 илл.
Теоретические основы
государственная академия
Конспект лекций предназначен для студентов, изучающих курс
"Теоретические основы теплотехники"
Конспект лекций посвящен изложению теоретических основ
теплотехники в краткой и доходчивой форме с учетом изучения материала
студентами специальности автомобили и автомобильное хозяйство. Курс, кроме
обеспечения современной энергетической подготовки инженеров-автомобилистов,
имеет и свою особую методику обобщенного раскрытия материала, позволяющую
сосредоточить главное внимание на выявлении более широких закономерностей и
новых возможностей развития энергетики.
Изложены теоретические основы технической термодинамики, теории
тепломассообмена, особое внимание уделено термодинамическим циклам
тепловых машин. Приводятся общие сведения о теплоснабжении и использовании
вторичных энергоресурсов, имеющих целью максимально экономное
расходование энергетических ресурсов
Изучение этого курса необходимо для глубокого понимания физической
сущности термодинамических процессов тепловых двигателей, ясного
представления о закономерностях энергопревращений в двигателях внутреннего
сгорания.
Для
студентов
специальности
АВТОМОБИЛЬНОЕ ХОЗЯЙСТВО".
7.090258
2
"АВТОМОБИЛИ
И
ОГЛАВЛЕНИЕ
1. Введение. Уравнение состояния. Теплоемкость.
2. Первый закон термодинамики
3. Термодинамические процессы идеальных газов
4. Второй закон термодинамики
5. Водяной пар
6. Влажный воздух
7. Общая характеристика компрессоров
8. Двигатели внешнего сгорания
9. Циклы газотурбинных установок
10. Циклы двигателей внутреннего сгорания
11. Основы теплообмена
12. Конвективный теплообмен
13. Теплообмен при фазовых превращениях
14. Теплообмен излучением
15. Теплопередача
16. Теплообменные аппараты
17. Топливо и процессы горения
3
Стр.
4
11
15
21
29
33
36
43
47
53
59
67
81
86
91
97
103
1. ВВЕДЕНИЕ. УРАВНЕНИЕ СОСТОЯНИЯ. ТЕПЛОЕМКОСТЬ
1.1 Теплотехника, ее предмет и метод
Теплотехника - наука, изучающая теорию и средства превращения энергии
природных источников в тепловую механическую и электрическую энергии, а
также использования тепла для практических целей.
Теоретические основы теплотехники включают термодинамику и теорию
тепломассообмена.
Основным методом теплотехники является термодинамический метод.
Сущность его состоит в том, что на основе изучения энергоэнтропийных балансов
в макроскопических системах устанавливают условие максимальной
эффективности тепловых машин и установок. Затем определяют пути
приближения к этим условиям.
1.2. Основные понятия и определения термодинамики
Термодинамика - наука о закономерностях превращения энергии в
макроскопических физических системах.
Техническая термодинамика - раздел термодинамики, рассматривающий
закономерности превращения тепловой энергии в другие виды.
Название "термодинамика" впервые применил Сари Карно (1824 г.) в работе
"Размышления о движущей силе огня и о машинах, способных развивать эту
силу".
"Терме" - тепло, жар, огонь.
"Динамикос" - сила, движение.
"Термодинамика" - движущая сила огня - дословный перевод с греческого.
В основу термодинамики положены два основных закона (начала),
установленных опытным путем.
- закон характеризует количественную сторону процессов превращения
энергии.
закон
характеризует,
устанавливает
качественную
сторону
(направленность) процессов в физических системах.
1.3. Термодинамическая система. Термодинамический процесс.
Термодинамическая система - совокупность макроскопических тел,
обменивающихся энергией между собой и с окружающей средой.
Термодинамический процесс - совокупность изменений состояния
термодинамической системы при переходе из одного состояния в другое.
1.4. Обратимые и необратимые процессы.
Равновесное состояние тела - такое, при котором во всех точках объема
параметры состояния одинаковы.
Равновесный процесс - процесс перехода термодинамической системы из
одного состояния в другое через равновесные состояния тела в любой момент
времени.
Неравновесный процесс - процесс, включающий неравновесные состояния.
Обратимый процесс - процесс, который протекает в прямом и обратном
направлении через одни и те же равновесные состояния.
4
Условия обратимости:
1. Отсутствие химических реакций.
2. Отсутствие внутреннего и внешнего трения.
3. Бесконечно медленное изменение состояния рабочего тела.
Необратимый процесс - процесс, который самопроизвольно протекает
только в одном направлении.
1.5. Рабочее тело. Термодинамические параметры состояния
Взаимное преобразование теплоты в механическую энергию в тепловых
машинах осуществляются при помощи рабочего тела.
В качестве рабочего тела обычно используют пар или газ, т.к. они обладают
значительно большим коэффициентом объемного расширения по сравнению с
жидкостями и твердыми телами.
Для однозначного определения состояния вещества вводятся физические
характеристики состояния вещества - параметры состояния.
Параметры состояния могут быть интенсивными и экстенсивными.
Интенсивные параметры не зависят от количества вещества, экстенсивные зависят. Пример - объем и температура.
Экстенсивные параметры, отнесенные к единице количества вещества,
приобретают смысл интенсивных. Их называют удельными.
Термодинамические параметры состояния - интенсивные свойства,
определяющие состояние тела или группы тел.
Обычно состояние однородного тела может быть однозначно определено
тремя параметрами - давлением, температурой и удельным объемом.
При наличии силовых полей (гравитационного, электромагнитного и др.)
состояние определяется неоднозначно.
1.6. Давление.
Давление - сила, действующая на единицу поверхности тела по нормали к
этой поверхности.
H
[р] = Па = 2
м
1 Па величина сравнительно небольшая. Поэтому вводят кратные величины
H
кH
1 кПа = 103 Па = 103 2 ;
1 кПа = 1 2 .
м
м
1 МПа = 106 Па = 103 кПа
1 бар = 105 Па = 102 кПа
Внесистемные единицы
1 мм Нg  133.3 Пa.
1 мм вод. ст.  9.81 Па.
Виды давления
1. Абсолютное, т.е. полное давление, отсчитываемое от абсолютного
вакуума.
рабс
5
2. Атмосферное (барометрическое) - абсолютное давление атмосферы Земли
в данной точке
рабс = В.
3. Избыточное давление - разность между абсолютным и атмосферным.
Параметром состояния не является.
pизб = pабс – B.
Избыточное давление иногда называют манометрическим (т.к. измеряется
манометрами).
4. Вакууметрическое давление - разность между атмосферным и
абсолютным.
pвак = B - pабс.
1.7. Температура
Температура характеризует тепловое состояние тела - степень "нагретости"
тела.
Температура - осредненная величина кинетической энергии хаотического
движения молекул.
Температура, при которой полностью прекращается движение молекул,
принята за начало отсчета. Температура тройной точки воды принята равной 273,
16 К (0, 010С).
[T]=K - единица измерения абсолютной температуры.
Температуру часто измеряют по шкале Цельсия.
[t]=C - единицы измерения температуры в обеих шкалах численно равны.
Температура по шкале Цельсия термодинамическим параметром состояния
не является.
T=t+273,15
t =T-273,15
t=T
За рубежом иногда пользуются шкалами температур Фаренгейта, Реомюра и
Ренкина.
1.8. Удельный объем.
Удельный объем - объем единицы массы газа.
V
м3
v  
v
m
кг
Плотность - величина обратная удельному объему.
1 m
кг
   ;   3 .
v V
м
1.9. Уравнение состояния идеального газа Менделеева-Клапейрона
Идеальный газ - модель газа, в которой молекулы не имеют объема и не
взаимодействуют друг с другом.
Совместное рассмотрение законов Бойля-Мариотта и Гей-Люссака
позволило Клапейрону в 1834 г. вывести уравнение состояния идеального газа
pv=RT - уравнение для 1 кг. газа (уравнение Клапейрона)
R - газовая постоянная
6
R  p v  H м  H м  Дж .
T м  кг К кг К кг К
3
2
Бойль Роберт (1627-1691). Англия. Физика, химия. Совместно с Мариоттом
не работал.
Мариотт Эдм (1620-1684). Франция. Механика жидкости и газа. Оптика.
Гей-Люссак Жозеф-Луи (1778-1850). Франция. Физика, химия.
Клапейрон Бенуа Поль Эмиль (1799-1864). Франция. Вывел уравнение
Клапейрона-Клаузиуса для водяного пара. Первым обратил внимание на работы
С.Карко, в которых был установлен II закон термодинамики.
pV=mRT- уравнение для газа массой m.
pV=RT- уравнение для 1 киломоля(уравнение Менделеева).
V - объем киломоля газа
Дж
R=8315
- универсальная газовая постоянная.
кмоль  К
8315
- формула для вычисления газовой постоянной.
R

1.10. Особенности реальных газов. Уравнение состояния реальных
газов Ван-дер-Ваальса
Уравнение состояния идеального газа можно применять в расчетах для
реактивных газов при низких давлениях и высоких температурах. При
нормальных условиях оно применимо для:
H2, He, O2, N2.
Углекислый газ (СО2) и некоторые другие дают отклонение до 2-3%.
Уравнение состояния реальных газов, учитывающие размер молекул, силы
взаимодействия между ними, образование комплексов молекул (ассоциаций) и пр.
имеют сложный вид.
В практике обычно используются таблицы и номограммы, построенные на
основе этих уравнений.
В общей форме в 1937-46 г. в СССР (Н.Н.Богомолов) и США (Дж.Мейер)
были выведены уравнения состояния реальных газов.
Наиболее простым, качественно правильно отображающим поведение
реальных газов, является уравнение Ван-дер-Ваальса (1873 г.).
a
( p  2 )( v  b )  RT ,
v
где b - поправка на объем молекул газа;
a
v2
- поправка на давление газа, учитывающая силы взаимодействия
молекул.
Уравнение Ван-дер-Ваальса позволяет качественно
поведение газов вблизи границ фазовых переходов.
анализировать
1.11. Смеси идеальных газов. Законы Дальтона и Амага
Парциальное давление - давление отдельного компонента смеси газов.
7
n
p см   pi - закон Дальтона
i 1
Абсолютное давление смеси газов равно сумме парциальных давлений
компонентов смеси.
n
V см   V i - закон Амагá
i 1
Полный объем смеси газов равен сумме приведенных к давлению и
температуре смеси объемов компонентов (парциальных объемов).
Законы Дальтона и Амагá позволяют получить уравнение состояния смеси
газов.
pсмVсм=mсмRсмTсм ,
где R см 
8314
.
см
Кажущаяся молярная масса смеси определяется из уравнения
n
 с м    i r i , где ri - объемные доли компонентов
i1
смеси
Пример: Полагая, что в воздухе 80% N2 и 20% О2
возд = 0,828 + 0,232 = 28,8 кг/моль
Газовая постоянная смеси может быть установлена из уравнения
R см   g i R i , где gi - массовые доли компонентов смеси.
Соотношение между массовыми и объемными долями определяется
выражением
i
r
, где ri - объемные доли компонентов смеси.
 i
Следует отметить, что всегда
gi 
n
n
g  1; r  1.
i
i1
i
i 1
1.12. Теплоемкость газов и газовых смесей. Истинная, средняя и
удельная теплоемкость. Зависимость теплоемкости от температуры
Теплоемкость - количество тепла, необходимое для нагрева тела на 1 К.
Дж
 С 
К
8
Удельная теплоемкость - количество тепла, необходимое для нагрева
единицы количества вещества на 1К.
Обычно различают следующие удельные теплоемкости:
1. Массовая - c
[c] =
Дж
кг  К
2. Объемная - с'
[c'] =
Дж
м3  К
Объем газа при этом должен быть приведен к нормальным условиям.
3. Мольная - с, где  - молекулярная масса.
Дж
[c] =
.
кмоль  К
Истинная теплоемкость определяется следующим аналитическим
выражением
dq
.
dt
c
Средняя теплоемкость в интервале температур t1 - t2 определяется из
соотношения
Cm 
q
.
t 2 - t1
В общем случае теплоемкость является функцией температуры, причем
обычно она возрастает с ростом температуры.
На рис.1.1 показана линейная зависимость удельной теплоемкости от
температуры, на рис.1.2 - степенная.
Если зависимость теплоемкости от температуры имеет сложный
нелинейный характер (как это показано на рис.1.3), то средняя теплоемкость в
интервале температур t1-t2 определяется из выражения:
t2
 C(t)dt
t1
C m tt 
2
t2  t1
1
9
В справочной литературе обычно приводятся значения истинной
теплоемкости при различных температурах, либо средние значения теплоемкости
в интервале температур 00С до t0C.
Тогда среднее значение теплоемкости в интервале температур от t1 до t2
определяется выражением:
C
t2
m t1

Cm tt  t 2  Cm tt  t 1
2
1
0
0
t2  t1
Эта формула применяема к массовой, объемной и мольной теплоемкостям.
Нагрев газов или паров может осуществляться при различных условиях.
Среди них можно выделить: 1. Нагрев при постоянном объеме;
2. Нагрев при постоянном давлении.
В первом случае теплоемкость процесса называют изохорной, во втором изобарной.
V=Const
qv = CV . t
p=Const
qp = CP.t
Во втором случае требуется подвод большего количества тепла, чем в
первом, т.к. в процессе подвода теплоты при постоянном давлении совершается
работа против внешних сил.
qv < qp.
Тогда соответственно
Сv < Сp
Изобарная и изохорная теплоемкости связаны уравнениями:
Сp - Сv = R - Майера
СР
 K - Пуассона
СV
К - коэффициент Пуассона.
Для одноатомных
газов К=1,67
(5/3)
- '' - двухатомных
- '' - К=1,40
(7/5) Теоретические
''
трехатомных
и
значения
многооатомных - '' - К=1.33
(4/3)
Обычно принимают К=1,29.

Теплоемкость газовых смесей вычисляется на основе уравнения теплового
баланса, из которого следует:
n
1. Для массовой теплоемкости смеси: C см   C ii  g i .
i 1
n
/
2. Для объемной теплоемкости смеси: C см
  C /i  ri .
i 1
10
2. ПЕРВЫЙ ЗАКОН ТЕРМОДИНАМИКИ
2.1 Теплота и работа
Энергия - единая скалярная мера различных форм движения материи.
Характеризует способность систем совершать работу.
Теплота - энергия хаотического движения и взаимодействия частиц тел.
Теплота является микрофизической формой передачи энергии от однонго тела к
другому при наличии разности температур между ними, причем при этом имеет
место обмен кинетической энергией между молекулами соприкасающихся тел,
либо перенос тепла электромагнитными волнами.
Работа - макрофизическая форма передачи энергии, связанная с
преодолением внешних силовых полей, либо сил давления.
2.2. Внутренняя энергия
В технической термодинамике считают, что внутренняя энергия включает:
1.
Кинетическую
энергию
поступательного,
вращательного
и
колебательного движения молекул.
2. Потенциальную энергию взаимодействия молекул (для реальных газов).
В более широком смысле внутренняя энергия включает также
внутриатомную (например, энергию движения электронов), внутриядерную
энергию и др. В термодинамике эти виды энергии не рассматриваются.
Для идеальных газов силы взаимодействия между молекулами приняты
равными нулю, поэтому u = u(T) - внутренняя энергия является однозначной
функцией температуры.
дЖ
Размерность удельной внутренней энергии u 
.
кг
В технической термодинамике знания абсолютного значения внутренней
энергии не требуется.
Обычно в технической термодинамике внутреннюю энергию отсчитывают
от 0С, а в теоретической - от 0 К - абсолютного нуля температур.
Для бесконечно малых изменений температуры в каком-либо процессе
du=CV•dT.
После интегрирования получим
u=u2-u1=CV(T2-T1). 
Отсюда следует, что изменение внутренней энергии не зависит от пути
процесса, а полностью определяется начальным и конечным состояниями.
2.3. Работа расширения рабочего тела
При подводе тепла к рабочему телу в общем случае помимо изменения его
внутренней энергии может совершаться работа.
Элементарная работа, отнесенная к 1кг рабочего тела (удельная работа)
определяется из соотношения
dl = pdv - элементарная работа расширения.
На рис. 2.1 в качестве примера показан цилиндр с поршнем . При
перемещении поршня из положения А в положение В совершается работа
расширения газа, определяемая из соотношения
11
V2
l   pdv
l ~ пл. 12341
V1
H м 3 Дж
l  p  v  2   .
м кг
кг
Работа
расширения
принимается
положительной, сжатия - отрицательной.
Численно
работа
пропорциональна
площади под кривой процесса.
Для тела произвольной формы при
изменении его объема (см. рис. 2.2) работа
изменения объема составит
dL  p  dFdn  pdV
F
Соответственно, если масса тела m , то
dl 
pdV
 pdv.
m
Работа зависит от пути процесса. В
качестве примера можно рассмотреть работу
процессов 1а2 и 1в2, показанных на рис. 2.2. Из рисунка видно, что l1a2>l1в2 т.к. пл.
1а2341 > пл. 1в2341
Работа расширения (сжатия) является функцией процесса.
12
2.4. Первый закон термодинамики.
Первым законом термодинамики называют закон сохранения и превращения
энергии (применительно к термодинамическим процессам).
Тепло, подведенное к рабочему телу, распределяется на изменение его
внутренней энергии и на совершение работы против внешних сил.
dq=du+dl - 1-й закон термодинамики в дифференциальной форме
Каждый из членов этого уравнения может иметь любой знак.
Правило знаков для теплоты. Подведенное тепло – принимается
положительным, отведенное - отрицательным.
Увеличение внутренней энергии - положительная величина, уменьшение отрицательная.
dq=du+pdv - первая форма записи 1-го закона термодинамики
В интегральной форме
V2
q  u2  u1   pdv или q = u + l.
V1
2.5. Энтальпия и энтропия
Дж. У. Гиббс предложил ввести термодинамическую функцию, имеющую
смысл полной (внутренней и внешней) энергии системы в виде
i=u+pv - энтальпия (теплосодержание)
i  u  Дж .
кг
Рассмотрим выражение 1-го закона термодинамики
dq=du+pdv=du+pdv+vdp-vdp=du+d(pv)-vdp=d(u+pv)-vdp.
В результате получаем
dq=di-vdp - вторая форма записи 1-го закона термодинамики.
P2
В интегральной форме q  i 2  i 2   vdp - для конечных изменений
P1
состояния рабочего тела.
Если давление в процессе p=Const, то qp=i2-i1. С другой стороны qp=Cp(T2T1). Следовательно, i=CpT и, соответственно, di=CpdT.
Изменение энтальпии газа равно равно количеству тепла, подведенному к
газу при постоянном давлении.
Энтальпия складывается из внутренней энергии рабочего тела (u) и работы
введения рабочего тела объемом v в среду с давлением p.
Название "энтальпия" введено в 1909 г. Каммерлинг-Онессом.
Энтропия. В 1852 г. Р. Клаузиус предложил ввести параметр, зависящий от
количества подведенной теплоты, и характеризующий изменение состояние
рабочего тела.
Для удобства рассмотрения многих термодинамических процессов вводится
понятие энтропии - приведенной теплоты.
13
dq
- формально энтропию можно рассматривать как
T
дифференциал которой определяется приведенным
dq  TdS, т.е. dS =
функцию, полный
выражением.
Очевидно, что если тепло подводится (dq>0), то энтропия возрастает, если
отводится - то энтропия убывает. Энтропия не может быть измерена
непосредственно, либо косвенным путем. Ее величину определяют в результате
расчета
S2
q   TdS - теплота процесса.
S1
2
dq
- изменение энтропии в процессе. Последнее выражение
T
1
непосредственно применяется для вычислений изменений энтропии в
термодинамических процессах.
Ts-диаграмма
В термодинамике для анализа работы тепловых машин весьма широко
используются энтропийные диаграммы (TS, iS и др.).
Наиболее распространена Ts-диаграмма (тепловая диаграмма). В этой
диаграмме площадь под кривой процесса пропорциональна количеству
подведенного тепла, как это показано на рис. 2.4
S  
S2
q   TdS .
dq=TdS;
S1
14
3. ТЕРМОДИНАМИЧЕСКИЕ ПРОЦЕССЫ ИДЕАЛЬНЫХ ГАЗОВ.
К частным термодинамическим процессам относят:
1. изохорный (V=Const);
2. изобарный (p= Const);
3. изотермический (T= Const);
4. адиабатический (изоэнтропный) (dq=0; S= Const);
Для всех частных процессов необходимо рассмотреть:
1. Математическое выражение (уравнение состояния).
2. Связь между параметрами состояния в начале и конце процесса.
3. Графическое изображение процесса в pv и TS координатах.
4. Количество теплоты, необходимое в процессе.
5. Изменение внутренней теплоты в процессе.
6. Изменение энтальпии в процессе.
7. Работу процесса.
8. Изменение энтропии в процессе.
Для этого следует воспользоваться следующими уравнениями.
1. pv=RT
2. du=CVdT
3. di=CpdT
4. dq=du+pdv; dq=di-vdp
5. dS =
dq
; TdS = du + pdv
dT
3.1. Изохорный процесс.
Изохорный процесс - процесс, происходящий при постоянном объеме.
1. v= Const
pv=RT;
2.
P R
  Const
T V
P1 P2

T1 T2
Давление газа пропорционально его температуре.
3.
4. dq=du+pdv=du=CvdT=TdS
dq=cvdt q=Cv(T2-T1)
15
Вся подведенная теплота расходуется на изменение внутренней энергии
рабочего
тела
5. du=CvdT u=Cv(T2-T1)
6. di=CpdT i=Cp(T2-T1)
7. dl=pdv=0; l=0
dq CV dT
8. dS = 
T
T
2
CV dT
T2
T2
S = S2  S1  
 CV ln ; S = CV ln
T
T1
T1
1
В TS - координатах график процесса - логарифмическая кривая.
Учитывая, что CV dT=TdS получим
dT
T

dS C V
3.2. Изобарный процесс.
Изобарный процесс - процесс, происходящий при постоянном давлении.
1. p=Const
pv=RT;
2.
V R
  Const
T P
V1 V2

T1 T2
Удельный объем газа пропорционален его температуре
3.
4. dq=di-vdp=di=CPdT=TdS
dq=di=cvdt q=CP(T2-T1)
Вся подведенная теплота расходуется на изменение энтальпии рабочего тела
5. du=CvdT u=Cv(T2-T1)
6. di=CpdT i=Cp(T2-T1)
7. dl=pdv=0; l=p(v2-v1)
Работа процесса равна произведению давления на изменение объема.
16
dq CpdT

T
T
2
CpdT
T2
T2
S = S2 - S1 = 
 Cp ln
S = Cv ln
T
T1
T1
1
8. dS 
В TS - координатах график процесса - логарифмическая кривая, которая
располагается более полого, чем изохора.
Учитывая, что CP=dT=TdS получим
dT T

dS CP
Следовательно, касательная, проведенная к кривой процесса в TS координатах, отсекает на оси S отрезок, численно равный изобаррной
теплоемкости CР.
3.3. Изотермический процесс.
Изотермический процесс - процесс, происходящий при постоянной
температуре.
1. T=Const
pv=RT; pV=Const
2.
p1 V2

p 2 V1
Удельный объем газа обратно пропорционален его давлению.
3.
RT
dv
v
p1
q = RTln
p2
4. dq=du+pdv=CvdT+pdv=
2
v2
RT
 RTln
v
v1
1
q=
5. du=CvdT=0
6. di=CPdT=0
7. dl  pdv 
RT
dv
v
2
RT
v2
dv = RTln
v
v1
1
l=
l = q = RTln
v2
p1
 RT ln
v1
p2
17
dq RTdv R

 dv
T
vT
v
2
R
v2
v2
p1
S = S2 -S1 =  dv  Rln
S = R ln = R ln
v
v1
v1
p2
1
8. dS 
Теплоемкость изотермического процесса бесконечно велика
q
 при T 0
T0 T
C = lim
3.4. Адиабатический (изоэнтропный) процесс.
Адиабатный процесс - процесс, совершающийся при отсутствии
теплообмена рабочего тела с окружающей средой.
1. dq=0
dq  di  vdp CpdT = vdp


dq

du

pdv
CvdT  pdv

Сp
Делим первое уравнение на второе
vdp
 K;
CV
pdv
dv dp
K

 0; после интегрирования получим
v
p

Klnv+lnp=Const
pvK=Const
2. p1v1K  p2v2 K
p1  v2 
 
p2  v1 
K
p1v1џv1K1  p2 v2 џv2K1
p1v1  RT1 ; p2 v2  RT2
Отсюда T1v1K1  T2 v2K1
T1  v2 
 
T2  v1 
K-1
Обе части возводим в степень
К1
и приравниваем левые части двух уравнений.
К
K-1
Тогда
T1  p 1  K
 
T2  p 2 
18
3.
4. dq=0
q=0
5. du=Cvdt u=Cv(T2-T1)
6. di=CpdT i=Cp(T2-T1)
l= - u= - Cv(T2-T1)= -
7. dl= - du
R
(T  T1 )
K1 2
1
(p v - p v ) l = -u
1- K 2 2 1 1
Работа совершается только за счет внутренней энергии.
dq
 0; S = Const
8. dS =
T
Адиабатный процесс является изоэнтропным.
Теплоемкость адиабатного процесса равна нулю
dq
C  0 т. к. С =
 0
dT
l=
3.5. Политропный процесс.
Политропный процесс - процесс, в котором изменяются все параметры
состояния, а теплоемкость остается постоянной.
1. С=Const
 CdT  C P dT  vdp
 dq  di  vdp
 


dq  du  pdv
CdT  CV dT  pdv
(C  C P )dT  vdp
Делим первое уравнение на второе

 (C  CV )dT  pdv
C  CP
vdp

n
C  CV
pdv
ndv dp

0
v
p
n ln v+ ln p=Const
pv n  Const
n=
C  CP
C  CV
C=CV
nK
n  1V
19
p 1 v 1n  p 2 v 2n
2.
v 
p1
  2
p2
 v1 
n
p 1 v 1 v 1n  1  p 2 v 2 v 2n  1
p 1 v 1  R T1 ;
p 2 v 2  R T2
О т с ю д а T1 v 1n  1  T 2 v 2n  1
v 
T1
  2
T2
 v1 
n 1
Обе части первого уравнения возводим в степень
части двух уравнений
n 1
T1  p1  n
 
T2  p 2 
3.
4. q=CdT;
q=C(T2-T1)
5. du=CVdT; u=CV(T2-T1)
6. i=CPdT;
i=CP(T2-T1)
7. dq=du+dl;
nK


dl  dq  du  CdT  CV dT   CV
 CV  dT 


n1
CV n  CV K  CV n  CV
CV ( K  1)
R
dT 
dT 
dT
n1
1 n
1 n
R
1
l
(T2  T1 ) 
( p v  p1v1 )
1 n
1 n 2 2
dq CdT
8. dS 

;
T
T
T2
n  K T2
S = Cln  C V
ln
T1
n  1 T1
n  K T2
S = C V
ln
n  1 T1

20
n1
и приравниваем левые
n
4. ВТОРОЙ ЗАКОН ТЕРМОДИНАМИКИ.
Первый закон термодинамики является частным случаем общего закона
сохранения и превращения энергии. Он устанавливает, что одна из форм энергии теплота может превращаться в другую работу и наоборот.
Первый закон термодинамики не определяет условий, при которых возможны
взаимные превращения этих форм энергии, т.е. не определяет направления
превращений.
Известно, что работу можно легко и полностью превратить в теплоту
(примеры - трение, удар, перемешивание в жидкостях и т.п.). Аналогично электрическую, как упорядоченную форму энергии.
Теплота сама по себе может переходить от нагретых тел к холодным, в то
время
как обратный процесс может быть осуществлен только при и определенных
условиях - затрате дополнительной энергии.
Теплоту можно превратить в работу только при наличии разности температур
между источником теплоты (теплоотдатчиком) и теплоприемником, причем
превратить всю теплоту полностью в работу нельзя.
Методологическое значение второго закона термодинамики в том, что на его
основе базируется теория тепловых двигателей, устанавливается максимальное
значение их КПД, определяется эффективность.
Второй закон термодинамики устанавливает критерий необратимости
процессов, позволяет находить наиболее эффективные пути осуществления
рабочего процесса.
Второй закон термодинамики раскрывает термодинамическую сущность
понятия температуры. Термодинамическая температура представляет собой
температуру тела по температурной шкале, основанной на использовании
двигателя Карно в качестве термометрического устройства.
Первые формулировки второго закона термодинамики были фактически даны
С.Карно (1824), который писал: "Нельзя надеяться, хотя бы когда-нибудь,
практически использовать всю движущую силу топлива". Под "движущей силой"
в те времена понимали энергию.
Теплота сама собой переходит лишь от тела с более высокой температурой к
телу с более низкой температурой, но никогда наоборот; некомпенсированный
переход тепла от тела с меньшей температурой к телу с большей температурой
невозможен (Клаузиус).
Нельзя осуществить тепловой двигатель, единственным результатом действия
которого было бы превращение теплоты какого-либо тела в работу без того, чтобы
часть этой теплоты передавалась другим телам (Томпсон).
Вечный двигатель второго рода невозможен (Освальд).
21
4.1. Термодинамические циклы.
Цикл
замкнутый
(круговой)
термодинамический процесс. Ранее уже
рассматривались
термодинамические
процессы, в которых внешняя работа
осуществлялась вследствие подвода тепла.
или изменения внутренней энергии рабочего
тела. При однократном расширении можно
получить ограниченное количество работы.
Далее температура и давление рабочего тела и
окружающей среды выравниваются.
Рабочее тело нужно возвратить в
первоначальное состояние для повторного
получения работы.
231 - lсж>lрасш - компрессоры и
холодильники
241 - lсж=lрасш
251 - lсж<lрасш - двигатели
Теперь рассмотрим цикл двигателя:
q1= l1+u
Внутренняя энергия определяется только параметрами
-q2= - l2-u
состояния в точках 1 и 2.
q1-q2=l1-l2=l4
lц - поезная работа цикла;
q1-q2 - использованное тепло.
4.2. Термический КПД.
Термический КПД (ТКПД) определяется как отношение полезной работы
цикла к подведенному теплу.
lц q  q
характеризует эффективность использования
t   1 2 тепла в цикле двигателя
q1
q1
t  1
Для циклов холодильных машин:
q
q2
 2 
- холодильный коэффициент цикла  < > 1
lц q1  q2
Для циклов тепловых насосов:

q1
q1

lц q1  q12
- отопительный коэффициент  > 1
22
4.3. Цикл Карно.
С. Карно исследовал циклы двигателей с целью нахождения оптимального с
точки зрения максимума ТКПД.
1. При подводе тепла по изотерме все тепло переходит в работу. Тело
сообщается с теплоотдатчиком.
2. При расширении по адиабате работа совершается только за счет энергии.
3. При сжатии по изотерме (изотермическом сжатии) тело сообщается с
теплоприемником. Вся работа сжатия переходит в отдаваемое тепло q2.
4. Cжатие по адиабате. Работа сжатия равна приращению внутренней энергии
тела. Рабочее тело возвращается с исходное состояние.
t 
q1  q 2

q1
v2
v
 RT2 ln 3
v1
v 4 T1  T2

v2
T1
RT1 ln
v1
RT1 ln
Теплоотдатчик и теплоприемник имеют постоянную температуру (Т1 и Т2).
t  1 
T2
T1
В термодинамике доказывается, что ТКПД цикла Карно не зависит от
природы рабочего тела (теорема Карно).
Сравнение ТКПД любого цикла с ТКПД цикла Карно позволяет судить о
степени совершенства данной машины. Цикл Карно служит эталоном при оценке
тепловых двигателей, хотя он реально неосуществим из-за ряда сложностей
технического характера.
4.4. Обратный цикл Карно.
Из постулата Клаузиуса следует, что передача теплоты от источника с
низкой температурой к источнику с высокой температурой обязательно требует
затрат энергии.
 
q2
q2
T2


lц
q1  q 2
T1  T2
23
4.5. Эквивалентный цикл Карно.
2
q1  q1a 2  T1cp ( S 2  S 1 )   Tds
1a
1
q 2  q 2b1  T2 cp ( S 2  S1 )   Tds
2b
t  1 
T2cp
T1cp
В качестве температур Т1 и Т2
подставляют
среднеинтегральные
значения температур в процессах подвода
и отвода тепла.
4.6. Обобщенный (регенеративный) цикл Карно.
С нагревателем и холодильником рабочее тело обменивается теплом только
в изотермических процессах 1-2 и 3-4.
t обобщ  t Ка р но  1 
T2
T1
В настоящее время созданы двигатели
Стирлинга, работающие по циклу, близкому
к регенеративному циклу Карно (две
изотермы, две изохоры).
4.7. Аналитическое выражение
второго закона термодинамики.
Изменение энтропии в необратимых процессах.
1. Алгебраическая сумма приведенных теплот для любого обратимого цикла
равна нулю.
dq
 T 0
1й интеграл Клаузиуса
Обратимый цикл содержит только обратимые процессы.
2. Алгебраическая сумма приведенных теплот для любого необратимого цикла
меньше нуля.
24
dq
 T 0
2й интеграл Клаузиуса
Цикл является необратимым, если он содержит хотя бы один необратимый
процесс.
Иногда оба интеграла Клаузиуса объединяют
dq
 T 0
Этот интеграл
термодинамики.
T1
обобщенный интеграл Клаузиуса
является
аналитическим
выражением
второго
закона
T1  T2 ; q 1  q 2
dq
dS 
T
 q1 q 2
S сист 

 0 т.к. T1 > T2
T1
T2
T2
Если в изолированной системе происходят необратимые процессы, то
энтропия системы возрастает.
Отсюда вывод Клаузиуса - энтропия мира непрерывно возрастает - тепловая
смерть ожидает вселенную. Критику этому дал Ф.Энгельс (Диалектика природы).
4.8. Физический смысл энтропии.
Энтропию нельзя измерить непосредственно. Ее смысл можно понять по
следующим интерпретациям.
1. Энтропия - мера ценности тепла - его работоспособности и технологической
эффективности.
Если рабочее тело совершает работу при температуре окружающей среды Т0 ,
то
l=q1-q0=q1-T0·S0
Для обратимого процесса в изолированной системе S0 = S1
l  q 1  T0 
Тогда
q1
T1
Отсюда видно, что чем больше Т1, тем больше работа, совершаемая системой.
Максимальное значение энтропии соответствует температуре окружающей
среды
S 0 max 
q
T0
Эту теплоту нельзя использовать.
2. Энтропия - мера потери работы вследствие необратимости реальных
процессов.
Чем более необратим процесс, тем больше возрастает энтропия
S2
dq  TdS ;
q =  Tds - для энергии, рассеянной в окружающей среде.
S1
25
3. Энтропия - мера беспорядка.
При подводе теплоты увеличивается хаотичность теплового движения, при
отводе - возрастает упорядоченность. При Т  0 в системе устанавливается
максимальный порядок.
lim S  0 Практически это проверить нельзя из-за недостижимости абсолютного
T0
нуля температур.
4.9. Эксергия теплоты.
Эксергия теплоты - максимально возможная работа, которую можно
получить из теплоты при условии, что теплоприемником является окружающая
среда

T0 
eq  q 1  1   ,
T1 

где q - подведенная теплота.
Если рабочее тело имеет температуру Т1* < Т1 вследствие необратимости
подвода тепла, то работа необратимого цикла Карно составит

T 
lH  q1  1  0*  ,
 T1 
Тогда потеря работоспособности вследствие необходимости подвода тепла от
теплоотдатчика к рабочему телу составит
T
q
T 
q 
l  eq  l H  q1  0*  0  = T0  1*  1   T0(Sрабочего тела - Sист.тепла)
T1 
T1 
 T1
 T1
l=T0·Sсист. - уравнение Гюи - Стодолы
Потери эксергии (работоспособности) теплоты характеризует совершенство
термодинамической системы.
При эксергетическом анализе часто применяют понятие эксергетического
КПД.
tек 
lH
eq
Гюи М. - французский физик, вывел уравнение Гюи-Стодолы в 1889 г.
Стодола Аурель (1859-1942) - словацкий теплотехник. Работы посвящены
созданию научных основ расчета турбин, ТАП. Одним из первых начал
заниматься газовыми турбинами, создал теорию инерционного регулятора.
Применил уравнение Гюи-Стодолы для решения теплотехнических задач, при
анализе эффективности работы силовых установок.
Термин "Эксергия" предложен в 1956 г. Ранее для обозначения этой величины
использовались термины "техническая работоспособность", "максимальная
техническая работа".
26
4.10. Теоретический цикл универсальной тепловой машины
Стирлинга.
В 1816 г. (до Карно!) шотландский священник Р.Стирлинг предложил цикл и
конструкцию универсальной тепловой машины. Ее можно использовать в качестве
двигателя, холодильника или теплового насоса.
Конструкция "Стирлинга" довольно сложна. Развитие техники только в 50-е
годы нашего столетия позволила создать машины, пригодные для практических
целей.
Цикл Стирлинга является по существу регенеративным циклом Карно,
состоящим из двух изотерм и двух изохор.
1-2 - изотермическое расширение газа
за счет подвода теплоты от нагревателя.
2-3 - изохорный отвод теплоты в
регенератор большой емкости с развитой
поверхностью теплообмена и малым
гидравлическим сопротивлением.
В качестве регенератора может
быть использована тонкая медная сетка.
3-4 - изотермическое сжатие газа с
отводом теплоты в холодильник
4-1 - изохорный подвод теплоты от
регенератора.
Если допустить, что в цикле Стирлинга осуществляется полная регенерация,
то его КПД равен КПД цикла Карно, т.е.
T
t  1  2
T1
Холодильный
и
отопительный
коэффициенты
Стирлинга
равны
соответствующим коэффициентам цикла Карно.
Возрождение интереса к машине Стирлинга объясняется повышением общего
уровня технической культуры, тенденцией к развитию многотопливных
двигателей, развитием холодильной техники, ядерных установок.
В последние десятилетия разрабатывались стирлинги с замкнутым рабочим
циклом. В качестве рабочего тела используют гелий или водород, обладающие
высокими теплопередаточными свойствами.
В действительном цикле протекают
процессы, приводящие к скруглению углов
цикла.
Примерные параметры цикла:
1. Максимальная температура 900-1000 к
2. Максимальное давление
100- 200 бар
3. t Kарно  0.7
4. Эффективный КПД
0,35...0,45
5. КПД регенератора
до 0,98
27
Во внешней камере сгорания можно сжигать различные топлива. К
преимуществам относят также малую токсичность отработанных газов,
малошумность и др.
Недостатки - сложность конструкции, худшие по сравнению с ДВС массовые
характеристики.
28
5. ВОДЯНОЙ ПАР.
Паром называется газ, находящийся в состоянии, близком к кипящей жидкости.
Парообразование – процесс превращения жидкого вещества в парообразное
Испарение – парообразование, происходящее при любой температуре с
поверхности жидкости.
Кипение - парообразование во всей массе жидкости приподводе к этой
жидкости теплоты.
Конденсация – обратный процесс.
Сублимация (возгонка) – переход твердого вещества непосредственно в пар.
Десублимация – обратный процесс.
5.1. Фазовая p – t диаграмма и тройная точка.
В p – v диаграмме изображены кривые
фазовых переходов.
ав – нагрев твердого тела
вс – нагрев жидкости
cd – перегрев пара
АВ, АК, AD – кривые равновесных состояний
А – тройная точка вещества.
Соответствует равновесию твердой, жидкой и газообразной фаз.
Для воды ta = 0.01 0C, жидкая фаза ?а = 0.001 м3 / кг ра = 610 Па
Температура кипения возрастает с повышением давления.
Температура, при которой жидкость закипает при заданном давлении, называется
температурой насыщения. Тн, tн
Соответствующее ей давление называется давлением насыщения Рн
Пар находящийся в динамическом равновесии с кипящей жидкостью,
называется влажным насыщенным паром. Т. о. Влажный насыщенный пар
является смесью мелкодисперсных частиц жидкости и сухого насыщенного пара.
Паросодержание (степень сухости пара) – массовое количество жидкости,
перешедшей в пар.
X 
m с . п.
m с . п.  m ж
Если Х = 1, то пар сухой
Степень влажности пара у = 1- х
Перегретый пар – пар с температурой, большей, чем температура насыщения.
Рассмотрим процесс порообразования при постоянном давлении и его
изображение в р – v координатах.
Ркр = 22.13 МПа
29
Ткр = 647.3 К
υкр = 0.00326 м3 / кг
а-в – нагрев жидкости
в-с – парообразование при Рн = const, Tн = const
c-d – перегрев пара
АК – нижняя пограничная кривая (Х = 0) – зависимость ?1 от р
КВ – верхняя пограничная кривая (Х = 1) – зависимость ?4 от р
Между ними обычно проводят линии равной сухости пара (Х = const).
Процесс парообразования (в – е) является изобарно – изотермическим.
Все параметры состояния на нижней пограничной кривой обозначают с
одним штрихом, на верхней – двумя штрихами.
Для удобства и упрощения расчетов полагают, что в тройной точке воды.
S 0  0

i0  0  Тогда u0 = i0 – p0υ0 = - 0.6 Дж / кг  0
Тогда удельная теплота жидкости на нижней пограничной кривой
определится так
q` = cp  tн = 4.19 tн ; q`  u` т.к.  υ  0
При дальнейшем подводе теплоты к жидкости начнется ее превращение в
пар.
Удельная теплота парообразования – количество теплоты, необходимое для
преобразования 1кг воды при температуре насыщения в сухой насыщенный пар.
Складывается из двух составляющих
r=ρ+ψ;
r = i`` – i`
ρ = u`` – u` – работа дисгрегации (разъединения) молекул жидкости.
Ψ = рн (υ`` – υ`) – внешняя пеплота парообразования (работа расширения).
5.2. Удельный объем влажного пара.
υх = υ` (1 - х) + ?`` х  υ`` х
при
х > 0.7
Очевидно, что в критической точке r = 0.В этой точке исчезает различие
между жидкостью и паром.
5.3. Энтропия жидкости определяется так
Тн
Тн
T
q
4.19T
S  S ` S 0  
 
 4.19l п н
T 273 T
273
273
0
30
5.4. Парообразование в TS – координатах.
r = S  Tн
S 
r
Тн
Теплота сухого пара
?`` = q` + r
Теплота влажного пара ?х = q` + r x
Теплота перегретого пара ?пер = q` + r +qпер
5.5. Уравнение Кланейрона – Клазиуса.
Элементарная работа в процессе парообразования
dl = (υ`` – υ`) dp
Затраченное на эту работу количество теплоты составит
dq = (S`` – S`) dT
Т. к. в этих элементарных циклах dl = dq, то получим уравнение Кланейрона
– Клаузиуса
dp S `` S `
r


dT  `` `` Т н ( `` `)
5.6. Таблицы водяного пара
Для расчетов термодинамичческих процессов водяного пара используются
таблицы водяного пара. В этих таблицах даются для различных значений
температуры и давление величины ?; υ; i; i; r; s; s;.Остальные параметры
вычисляют.
Для инженерных расчетов вместо таблиц часто используют i – s – диаграмму
водяного пара.
5.7. i – S диаграмма водяного пара.
Предложена Молье в 1904 г. Основное преимущество – работа и теплота,
участвующее в процессе изображаются отрезками линий, а не площадями. Не
нужен планиметр, как для подсчета по TS иPυ диаграммам.
dS 
T (
dq p di
T T
i
) p - изоборы прямые линии
s
При низких давлениях изотермы весьма близки к горизонтальным прямым.
Для идеального газа изотермы в i – s диаграмме являются горизонтальными
отрезками.
31
Обычно на i –s диаграммы наносят также изохоры, которые идут круче
изобар i – s диаграммы позволяют давать грубую оценку теплоты и работы в
различных процессах. Для более точных расчетов пользуются таблицами М. П.
Вукаловича.
С i – s диаграммой более подробно можно познакомится на практических
занятиях.
32
6. ВЛАЖНЫЙ ВОЗДУХ
6.1. Основные определения и характеристики.
В атмосферном воздухе всегда содержится влага в виде водяного пара, т. е.
Атмосферный воздух представляет собой их смесь.
Влажный воздух – смесь сухого воздуха с водяным паром.
Давление водяного пара в атмосферном воздухе невелико, причем пар
находится в перегретом состоянии, поэтому влажный воздух можно считать
смесью идеальных газов.
По закону Дальтона давление влажного воздуха равно сумме парциальных
давлений сухого воздуха и водяного пара
pбар = p + pп
На р - ? диаграмме водяного пара точка А
соответствует состоянию перегретого пара,
точка В – состоянию сухого насыщенного пара.
Очевидно,
что
при
постоянном
парциальном давлении перегретый водяной
пар, содержащийся во влажном воздухе, может
стать насыщенным только при понижении
температуры воздуха, т. к. tВ < tА.
Смесь сухого воздуха и насыщенного водяного пара называется
насыщенным влажным воздухом.
Смесь сухого воздуха и перегретого пара – ненасыщенный влажный воздух.
Температура, до которой необходимо охлаждать ненасыщенный влажный
воздух, чтобы он стал насыщенным, называется температурой точки росы. При
дальнейшем охлаждении воздуха образуется туман (часть пара переходит в
капельно – жидкое состояние).
Обычно влажный воздух имеет низкое давление (близкое к атмосферному),
а парциальное давление водяного пара в нём невелико. Поэтому его свойства
близки к свойствам идеального газа.
Все удельные величины, характеризующие влажный воздух, относят к 1 кг
сухого воздуха (а не смеси!).
1.
6.2. Основные параметры влажного воздуха.
Абсолютная влажность – количество водяного пара, содержащегосяв 1м3
влажного воздуха
п =
2.
mп
;
Vп
Vп = 1м3
[ρ] = кг / м3
Относительная влажность – отношение абсолютной влажности к
максимально возможной при той же температуре

п
p
= п
 п max p п max
обычно [φ] = %
33
3.
т. к. соотношение плотностей равно соотношению давления для
идеальных газов.
Влагосодержание – отношение массы пара к массе сухого воздуха
d
4.
mп Rв  Tв  Pп  Vп 287 Pп
Pп
  Pн
=


 0.622
 0.622
;
mcв Rп  Tп  Pв  Vв 462 Pв
P  Pп
P    Pн
[d] = г / кг с. в.
Парциальное давление водяного пара .
Выражение можно получить из предыдущего уравнения
d  p – d  pп = 0.622 pп
pп ( 0.622 + d ) = d  p
pп =
5.
dp
0.622  d
[pп] = Па
Энтальпия влажного воздуха
J=Jв + Jп = Ср t + (2500 + 1.97 t)  d
r – теплота парообразования
J   кДж
кг
6.
Температура мокрого термометра – температура, при которой воздух
находится в состоянии насыщения после изоэнтальпического
охлаждения
i – d диаграмма
Предложена в 1918 г. Л. К. Рамзиным. i – d диаграмма построена в
косоугольной системе координат.
7. Точка росы – температура, при которой влажный воздух становится
насыщенным, а водяной пар – сухим насыщенным (? = 100 %).Образуется туман.
6.3. Определение влажности.
Существует несколько способов и приборов для определения влажности.
Среди них наиболее часто применяют следующие приборы.
1. Волосяной гигрометр. Применяются в бытовых приборах. Точность
невелика.
2. Психрометр. Применяются в метеорологии, устанавливаются в музеях,
картинных галереях и т. п. Состоит из двух идентичных термометров – “сухого” и
“влажного”. Шарик “влажного” термометра обернут мокрой лентой,
обеспечивающей подвод воды к шарику.
Если относительная влажность воздуха меньше 100%, то температура,
“мокрого” термометра всегда меньше, чем “сухого”. Оба термометра заключены
в заградительные кожухи и обдуваются в процессе измерений воздухом от
вентилятора.
34
По показаниям двух термометров с помощью психрометрических таблиц
или i – d диаграммы можно определить абсолютную и относительную влажности
воздуха.
С i – d диаграммой и устройством психрометра можно познакомится на
практических занятиях.
Рис. 6.2.
35
7. ОБЩАЯ ХАРАКТЕРИСТИКА КОМПРЕССОРОВ.
7.1 Одноступенчатый поршневой компрессор, его устройство, цикл и
КПД.
Компрессор – машина, предназначенная для сжатия и перемещения газов и
паров.
Компрессоры классифицируют по следующим признакам.
1. По роду сжимаемой среды: воздушные, газовые, паровые.
2. По принципу действия:
объемные – поршневые, ротационные;
лопастные – осевые, центробежные;
Иногда встречаются струйные компрессоры (точнее насосы).
3. По степени повышения давления (  k 
p2
p1 ):
компрессоры низкого, среднего и высокого давления;
или вентиляторы, нагнетатели и собственно компрессоры.
Кроме того, компрессоры классифицируют по конструктивным признакам
(число и расположение цилиндров, число ступеней сжатия), наличию системы
охлаждения и т. д.
К объемным компрессорам относят поршневые,
ротационные и шестеренчатые.
Одноступенчатый
поршневой
компрессор,
схематическое устройство которого изображено на рис.
15.1, состоит из следующих элементов:
1 – цилиндр; 2 – поршень; 3 – впускной клапан; 4 –
выпускной клапан;
5 – система охлаждения цилиндра;
6 – кривошипно шатунный механизм.
Ротационный компрессор (см. рис. 15.2)
включает корпус 1, в котором эксцентрично
установлен ротор 3 с подвижными пластинами
2. При вращении ротора объем газа между
двумя соседними пластинами уменьшается,
поэтому повышается давление газа.
Цикл идеального компрессора представлен на рис. 15.3 в рν – координатах.
Он состоит из следующих процессов:
4-1 – заполнение цилиндра при давлении р1; 1-2
– сжатие газа до требуемого давления р2; 2-3–
выталкивание сжатого газа через выпускной клапан
Клапаны в компрессорах обычно открываются
автоматически при достижении заданного давления.
Линия всасывания 4-1 и нагнетания 2-3 не
являются термодинамическими процессами, т. к.
состояние рабочего тела на этих линиях остается
36
постоянным, а изменяется лишь количество рабочего тела.
Общая работа сжатия составит
k  p11  p22 
1
( p11  p22 ) ,
n 1
где n – показатель политропы сжатия.
После преобразований получим
k 
n
( p11  p22 )
n 1
Если сжатие осуществляется по изотерме, то p11  p22 , следовательно
 k   p11  n
p2
p1
При сжатии по изотерме работа сжатия меньше, чем при сжатии по
политроне или адиабате.
На рис. 15.4а показаны циклы идеального компрессора со сжатием по этим
трем процессам. При сжатии по изотерме работа цикла минимальна. На рис. 15.4б
представлены процессы сжатия в TS – координатах.
Для приближения процесса сжатия к изотермическому применяют
охлаждение компрессоров (обычно водяные).
Для охлаждаемых компрессоров вводятся понятие изотермического КПД
из 
 из
 пол
обычно ηиз  0.65…0.75
Для неохлажденных компрессоров введено понятие адиабатного КПД
 ад 
 ад
 пол
Значение ηад составляют 0.7…0.9
Потери на трение в механизмах учитываются механическим КПД
Обычно для поршневых компрессоров
 м  0 . 85
37
Тогда эффективный КПД составит
  из м
к  ад  м
или
В реальных поршневых компрессорах всегда имеется вредное пространство,
определяемое объемом между крышкой цилиндра и поршнем, находящимся в
верхней мертвой точке.
Часть газа, оставшаяся в вредном пространстве, при движении поршня от
верхней мертвой точки вниз, расширяется. Поэтому полезный рабочий объем
цилиндра уменьшается.
Если Vh – рабочий объем цилиндра;
V0 – объем вредного пространства,
то
V1-V4 – действительный объем всасывания.
Vh – V1 – всегда
При повышений давления величина действительного объема всасывания
уменьшается и в пределе может достигнуть нуля.
Объемный КПД компрессора учитывает влияние вредного пространства
 
V1  V4
Vh
обычно   0.75...0.90
7.2. Многоступенчатый поршневой компрессор.
При увеличении степени повышения давления объемный КПД поршневого
компрессора уменьшается. Кроме того, несмотря на охлаждение, температура газа
или воздуха в конце процесса сжатия достигает  2000С, что может привести (и
приводит) к вспышкам масла, смазывающего стенки цилиндра, вследствие его
разжижения и повышения температуры.
В силу указанных причин для одноступенчатых поршневых компрессоров
величина степени повышения давления
k 
p2
p1
обычно не превышает 10
Для достижения больших давлений
применяют многоступенчатые компрессоры с
промежуточным охлаждением газа после
каждой ступени сжатия.
Схематическое
устройство
двухступенчатого поршневого компрессора с
промежуточным охлаждением приведено на
рис. 15.5а
Рис. 15.5. (а)
38
Оба цилиндра компрессора охлаждаются водой. Кроме того, после сжатия в
ступени I газ поступает в промежуточный холодильник, также охлажденный
водой.
Цикл этого компрессора изображен на рис.
15.5б. заштрихованная площадка пропорциональна
по площади работе, на которую уменьшилась
суммарная работа цикла.
Промежуточное охлаждение позволяет
приблизить процесс сжатия к изотермическому.
На рис. 15.5в показаны процессы сжатия и
промежуточного охлаждения в TS – координатах.
Обычно степень повышения давления во
всех ступенях принимают одинаковой, т. е.
k 
ст
p
p2 p3

 .....  i 1
p1 p1
pi
7. 3. Лопаточные компрессоры.
Лопаточные (лопастные) компрессоры иногда называют турбокомпрессорами.
В лопаточных компрессорах газу сообщается кинетическая энергия, которая
затем преобразуется в потенциальную. Оба этих процесса происходят в
непрерывном режиме.
Лопаточные машины обратимы (турбины и компрессоры).
По направлению потока рабочего тела лопаточные машины делятся на
осевые и центробежные. Иногда встречаются диагональные машины.
7.4. Осевой компрессор.
39
Планы скоростей осевых
ступеней
обычно
строят
методом наложения окружных
скоростей.
Энергообмен в ступени
определяется
  u  Wu
Дж м 2
[ ] 
 2
кг
с
Рис. 15.6.
Мощность на привод компрессора
Ni    G ;
[N] = Вт, т.к. [G] = кг/с
В осевых компрессорах процесс сжатия воздуха происходит как в рабочем
колесе, так и в спрямляющем аппарате.
Степень повышения давления в одной ступени обычно невелика, поэтому
для достижения больших давлений приходится устанавливать целый ряд рабочих
колес и спрямляющих аппаратов.
Число ступеней в некоторых многоступенчатых компрессорах достигает 14 в
одном каскаде
Степень повышения давления в одной степени до 1.35. для сверхзвуковох
ступеней до 2.
7.5. Центробежный компрессор
  u2C2u  u1C1u
Центробежные компрессоры обеспечивают повешение
давления до 4 – 4.5 раз в одной ступени.
40
7.6. Изображение процесса сжатия в лопаточном компрессоре.
1-2 – реальный процесс
1-2 – идеальный процесс
Внутренний кпд ступени осевого компрессора составляет 0.8 – 0.92, а
ступени центробежного – 0.8 – 0.86.
Вентиляторы часто не имеют спрямляющего аппарата. Выпускается серийно
с диаметроми рабочих калес от 200 мм до 2000 мм.
Давление, развиваемое вентиляторами, лежит в пределах 30 – 12000 Па.
7.7. Вентиляторы. Назначение и принцип действия осевых и
центробежных вентиляторов. Классификация и подбор вентиляторов.
Вентилятор – устройство с рабочим органом в виде лопаточного колеса.
Предназначены для сжатия воздуха со степень повышения давления до 1.15 и
его перемещения.
Наиболее распространены радиальные (центробежные) и осевые
вентиляторы.
Принцип действия и тех и других вентиляторов не отличается от работы
ступеней лопаточных компрессоров. Спрямляющий аппарат у вентиляторов
обычно отсутствует.
КПД вентиляторов осевых несколько больше, чем центробежных.
7.8. Классификация и подбор вентиляторов
Вентиляторы обычно проектирует сериями. Номер вентилятора соответствует
диаметру рабочего колеса в дециметрах.
По величине создаваемого давления вентиляторы подразделяют на
вентиляторы:
низкого давления – до 1000 Па;
среднего давления – до 3000 Па;
высокого давления – до 15000 Па.
Вентиляторы общего назначения и целый ряд специально стандартизованы,
поэтому всегда следует по мере возможности применять серийно выпускаемое
оборудование.
7.9. Характеристики вентиляторов.
Характеристика вентилятора – зависимость давления, потребляемой
мощности и КПД от его объемной
производительности.
Работу вентилятора всегда стараются обеспечить на правой ветви напорной
характеристики вблизи максимума КПД.
7.10. Применение вентиляторов
Вентиляторы используются во многих областях. Примеры:
1. Системы вентиляции и кондиционирования воздуха;
2. Тягодутьевые вентиляторы в тепло энергетике;
3. Вентиляторы систем охлаждения машин и механизмов;
41
4. Специальные вентиляторы (шахтные, карьерные, метрополитен);
5. Вентиляторы систем пневмотранспорта.
Подбор вентиляторов осуществляют с учетом требуемого давления,
производительности по каталогам и справочникам, в которых приведены основные
характеристики.
Иногда проектируют и изготавливают вентиляторы по требованиям
конкретной установки, машины или механизма, причем при создании новой
техники этот вопрос приходится решать довольно часто.
42
8. ДВИГАТЕЛИ ВНЕШНЕГО СГОРАНИЯ
Предлагаемый Вашему вниманию доклад посвящен поискам путей
оптимизации рабочих процессов и параметров автомобильных двигателей
Стирлинга. Такие двигатели привлекают внимание специалистов своим высоким
КПД, способностью работать от любых источников тепла, в том числе низкого
потенциала. Одним из важнейших условий, предъявляемых в настоящее время к
любым энергетическим установкам, помимо КПД, является экологическая
чистота. Двигатели Стирлинга, являются одними из наиболее совершенных
устройств, в комплексе удовлетворяющих указанным требованиям. Поэтому
весьма перспективным представляется использование двигателей Стирлинга для
силовых установок автомобилей, особенно для внутригородского транспорта.
Двигатели Стирлинга, основные модификации которых представлены
схематически на плакате 1, являются одними из наиболее эффективных
преобразователей энергии. В настоящее время тепловые машины Стирлинга в
основном находятся в стадии опытно-конструкторских разработок. Накоплен (к
сожалению, в основном за границами СНГ) некоторый опыт их расчетов,
проектирования, изготовления и эксплуатации. Теоретически и экспериментально
характеристики таких машин исследованы в значительно меньшей степени, чем
ДВС, ГТУ, ПСУ. Поиски и новые разработки в этом направлении постоянно
продолжаются.
Широкому применению двигателей этого типа препятствует наличие ряда
нерешенных проблем, в числе которых - правильный выбор параметров. К другим
следует отнести необходимость создания рациональных методов расчета
характеристик двигателей. До настоящего времени не создана универсальная и
достаточно надежная методика оптимизации, хотя проведены многочисленные
теоретические и опытные исследования как отдельных узлов, так и двигателей в
целом.
Цель работы
Исходя из вышеприведенного определились цели проводимых исследований,
а именно:
1. Сравнительный анализ параметров известных схем и моделей машин
Стирлинга.
2. Создание методики теплового, гидравлического расчета параметров
двигателей.
3. Исследование соотношений видов потерь энергии в машинах с целью с
целью дальнейшей оптимизации их параметров.
4. Разработка методов расчета характеристик двигателей.
В предлагаемой Вашему вниманию работе рассматривается метод расчета
рабочих процессов и оптимизации параметров тепловых машин Стирлинга,
позволяющий повысить их мощность и КПД. Эта оптимизация может проводиться
уже на стадии предварительной проработки вариантов построения машин.
Предлагаемая методика не претендует на полную завершенность, поскольку
исследования в данном направлении продолжаются, однако ее основные
положения и принципы уже дают обнадеживающие результаты. Конечной целью
является определение основных параметров двигателей на основе замкнутой
43
оптимизации, позволяющей наилучшим образом выбирать основные соотношения
его узлов и деталей на стадии конструирования.
8.1. Расчет параметров действительных циклов
Известные методы расчета параметров действительных циклов двигателей
проводятся обычно по ступенчатой схеме. На первом этапе определяются и
выбираются параметры идеального цикла, чаще всего на основе теории Шмидта,
на втором - вычисляются параметры действительного цикла с учетом тепловых,
гидравлических и др. потерь во внутреннем контуре двигателя. Последующие
этапы предполагают определение основных характеристики двигателя с учетом
механических, внешних тепловых и др. потерь.
Однако ступенчатая схема расчетов параметров двигателей может быть
применена далеко не всегда. Ее нельзя использовать, например, при оптимизации
по внутреннему или эффективному КПД двигателя, поскольку для любых
соотношений его параметров КПД идеального цикла определяется только
температурами источников теплоты. Аналогичным образом обстоит дело при
оптимизации по ряду других параметров, в частности, литровой мощности и др.
Поэтому в общем случае всегда следует отдавать предпочтение полной
оптимизации параметров двигателя по какому-либо из них, либо комплексу из
этих параметров. Так, для транспортных двигателей, оптимизацию обычно осуществляют по какому-либо из параметров мощности, т.е. в какой-то мере по
удельной массе, для стационарных силовых установок - по удельному расходу
топлива, т.е. по эффективному КПД. Возможны и другие критерии оптимизации в
зависимости от назначения двигателя и условий его работы.
Оптимизация предполагает получение для двигателя максимального
значения такого параметра, который в данном варианте его практического
применения следует считать наиболее важным (этот параметр в дальнейшем
называется оптимизируемым), и вычисление остальных характеристик машины и
соотношений между ними, которые именуются оптимальными. В процессе
оптимизации на начальном этапе производится расчет идеального цикла, а затем
действительного, причем в ходе вычислений корректируются параметры как
исходного, так и действительного циклов с учетом геометрических характеристик
двигателя, различного рода потерь, рода рабочего тела, действительных
температур и др.
Предлагаемый порядок вычислений параметров действительных циклов и
двигателей путем замкнутой оптимизации представлен на плакатах 2,3.
Варьируемыми параметрами помимо тех, традиционно используются при
оптимизации идеальных циклов, являются длина и диаметр трубок нагревателя и
охладителя, а также параметры насадки регенератора. Методика позволяет учесть
конечную разность температур на внутренних поверхностях теплообменников,
гидравлические потери в теплообменниках и регенераторе, неполноту
регенерации, процессы теплообмена непосредственно в цилиндрах двигателя,
механические потери на трение. В процессе вычислений учитывается изменение
вязкости и теплопроводности рабочего тела в зависимости от его температуры.
Модель и методика расчета позволяют находить оптимальные геометрические
соотношения двигателей, определять их внутренний и эффективный КПД,
оценивать влияние отдельных величин на параметры двигателя.
44
8.3. Результаты исследований
В качестве примера, подтверждающего достоинства замкнутой
оптимизации, в верхней части на плакате 4 в виде таблицы представлены
результаты расчетов двигателей -модификации с эффективной мощностью 32
кВт. Опытные образцы двигателей этой модификации испытывались за рубежом
на автомобилях, поэтому исследованы параметры подобного двигателя. Из
таблицы видно, что при оптимизации идеальных циклов по параметру работы
wmax параметры действительного цикла практически совпадают с параметрами
двигателя, оптимизированного по параметру мощности Z. Однако оптимизация
по параметру Z2 уже дает существенные отличия, как это и предполагалось
Д.Киркли. Оптимизация по параметру Z3 приводит к уменьшению габаритов
двигателя за счет сокращения объемов нагревателя, охладителя и регенератора,
однако при этом, как и при оптимизации по Z2, значения внутреннего и
эффективного КПД невелики.
Интерес представляют результаты оптимизации по значениям внутреннего и
эффективного КПД двигателя. В первом случае получена достаточно высокая
величина i, как это видно из таблицы, однако достигается это за счет роста
объемов теплообменников, цилиндров и регенератора, что способствует
уменьшению гидравлических потерь, улучшению процессов теплообмена и
регенерации. В то же время увеличение размеров цилиндров приводит к резкому
уменьшению механического КПД и, соответственно, эффективного КПД.
Оптимизация по эффективному КПД дает вполне удовлетворительные результаты
и ее можно рекомендовать для расчетов высокоэкономичных двигателей.
Оптимизация по литровой мощности двигателя дает примерно такие же
результаты, как и оптимизация по параметру Z. Оптимизацию по удельной работе
действительного цикла нельзя признать удачной вследствие крайне низких
значений внутреннего и эффективного КПД.
Предлагаемые Вашему вниманию модель и методику расчета не следует
считать окончательными и завершенными. Они обладают просматриваемыми
потенциальными возможностями с точки зрения углубления качественных
характеристик и расширения количественных параметров.
Так, например, допускается практически неограниченное введение
корректирующих и дополняющих зависимостей. Имеется возможность выявить
влияние отдельных элементов и параметров двигателей на их характеристики.
Становится возможным исследование программ регулирования двигателей,
переходных режимов и др. Так, например, сейчас расчетные уравнения уточнены с
учетом значений "мертвых объемов" цилиндров и "мертвых объемов" между
нагревателем и регенератором, между охладителем и регенератором. Проводятся
расчеты для других рабочих тел (H2, Ar, воздух). Оцениваются количественно
различного рода потери в двигателе и др.
Среди качественных характеристик следует выделить возможность перехода
на расчеты параметров двигателей иных схем. В качестве примера на плакате 5
приведены идентичные по форме представления результаты оптимизации
проектируемого 8-цилиндрового автомобильного двигателя двойного действия
мощностью 160 кВт.
45
Заключение
Проведенные и выполняемые в настоящее время исследования двигателей
Стирлинга позволяют сделать следующие выводы:
1. Предложена изотермическая модель идеального цикла машин Стирлинга на
базе цикла Шмидта, позволяющая более полно отобразить соотношения
параметров и процессы в двигателе.
2. Обоснована методика замкнутой оптимизации параметров действительных
циклов двигателей, учитывающая их геометрические характеристики, кинематику,
процессы теплообмена и регенерации, гидравлические и механические потери.
3. Разработаны методика, программы расчетов и оптимизации параметров
двигателей -, - и -модификаций, с ромбическим механизмом, двойного
действия, позволяющие определять их основные характеристики на этапе
конструирования.
4. Предложены новые схемы двигателей Стирлинга, позволяющие повысить их
мощность и экономичность.
5. Выявлены возможности двигателей новых схем, проанализированы их
некоторые качественные и количественные характеристики.
6. Проведены предварительные проработки конструкции транспортного двигателя
Стирлинга для грузового автомобиля.
В дальнейшем предполагается проведение исследований в следующих
направлениях:
1. Выявление критериев оптимизации параметров двигателей исходя из
особенностей их конструкции, практического применения и условий
эксплуатации.
2. Эксергетический анализ двигателей и энергетических установок с целью поиска
путей повышения их эффективности.
3. Разработка методов определения характеристик двигателей на нерасчетных
режимах и программ их регулирования.
4. Создание расширенных моделей транспортных силовых установок, тепловых
насосов, комплексных систем теплоснабжения, вентиляции и кондиционирования
зданий и сооружений, позволяющих оптимизировать их параметры на этапах
проектирования.
5. Анализ качественных и количественных характеристик двигателей новых схем.
46
9. ЦИКЛЫ ГАЗОТУРБИННЫХ УСТАНОВОК
9.1. Общая характеристика газотурбинных установок
Газотурбинные установки - тепловые машины, у которых для получения
полезной работы используется газовые турбины.
Газовая турбина - тепловой турбинный двигатель, в лопаточном аппарате
которого энергия газового потока превращается в механическую энергию
вращающегося вала.
9.2. Основные преимущества ГТУ
1. Возможность адиабатного расширения рабочего тела до атмосферного
давления, что повышает т.к. п.д. цикла.
2. Большая единичная мощность установок . В настоящее время мощность
стационарных ГТУ достигает 100 тыс. КВт
(100МВт). Основными направлениями развития нашей страны на 1986-90 годы и
на период до 2000 года предусмотрено строительство газовых энергетических
турбин единичной мощностью до 150тыс.кВт
3. Небольшие габариты и масса. Удельная масса транспортных ГТУ
примерно на порядок ниже чем удельная масса поршневых д.в.с.
4. Отсутствие деталей с возвратно-поступательным движением и, как
следствие этого, высокий механический и.н.д.
м0,99
Помимо этих преимуществ ГТУ имеют ряд недостатков, роль которых
постепенно снижается по мере совершенствования ГТУ. О них мы упомянем
позже.
9.3. Краткая история развития газотурбинных установок
Первые газовые турбины в России были созданы в 1897г. инженером
Кузьминским П.Д. Он построил радиальную центробежную турбину со сгоранием
топлива при постоянном давлении .
В 1906 - 1908гг. инженер Караводин В.В. создал ГТУ со сжиганием топлива
при постоянном объеме.
В 1939г. профессор Харьковского политехнического института В.М.
Маковский разработал ГТУ мощностью 400 кВт, которая была построена на ХТГЗ
им. С.М. Кирова (ныне объединение Турбоатом) и установлена в г. Горловке
(Донбасс). В качестве топлива использовался подземный газ.
Промышленное использование ГТУ началось в 1939г. в СССР и Швейцарии.
Наибольшее развитие и внедрение ГТУ получили в авиации с конца 40х годов.
Позже их стали применять также на судах и локомотивах.
В настоящее время к. п. д. ГТУ достигает ~ 35%, а отдельные
экспериментальные агрегаты и уникальные авиационные двигатели имеют
термический к. п. д. , достигающий 50% .
9.4. Требования к конструкционным материалам.
Материалы, применяющееся в турбостроении, должны отвечать следующим
требованиям:
47
1. Высокая механическая прочность.
2. Жаропрочность и жаростойкость.
3. Химическая и коррозионная стойкость.
4. По возможности низкая стоимость.
Материалы должны обеспечивать срок службы ГТУ до капитальной
переборки не менее 100 тыс. часов. В настоящее время срок службы для
транспортных установок достигает 20-50 тыс. часов
Авиационные ГТД имеют, как правило, срок службы в несколько тысяч, а
иногда и сот часов.
В настоящее время температура газов перед турбиной достигает 1300К. Для
обеспечения таких высоких параметров цикла применяют охлаждение лопаток
рабочего колеса и соплового аппарата. Начинают использоваться керамические и
другие специальные материалы.
В отдельных образцах авиационных ГТД достигнута температура газов
перед турбиной 1640К. (фирма Rolls-Roys)
9.5. Схема и цикл ГТУ с подводом тепла при постоянном давлении
1-2 - адиабатное сжатие воздуха в компрессоре;
2-3 - изобарный подвод тепла;
3-4 - адиабатное расширение рабочего тела в турбине;
4-1 - изобарный отвод теплоты с продуктами
сгорания в атмосферу.
9.6. К. п. д. ГТУ
t = 1 - q2/q1 ;
q1 = Cp(T3-T2) ;
q2 = Cp(T4-T1) - тело подводится и отводится в изобарных
процессах.
t = 1 - (T4-T1)/(T3-T2)
 = U3/U2 ;
 = P2/P1 = P3/P4 - обозначения
k-1/k
T4 = T3/
;
T3 = T2 ;
T2 = T1k-1/k
t = 1 - T1-T1/(k-1/k - k-1/k)T1 = 1-1/k-1/k
t = 1 - 1/ k-1/k
48
Термический к. п. д. ГТУ непрерывно возрастает с увеличением степени
повышения давления  (часто эту величину обозначают  ) и показателя адиабаты
К
9.7. Схема и цикл ГТУ с подводом тепла при постоянном объеме.
Отличается от предыдущей ГТУ тем, что камера сгорания содержит
клапаны, позволяющие периодически изолировать камеру сгорания от
компрессора, топливного насоса и турбины и обеспечивать воспламенение и
сгорание топлива при практически постоянном объеме.
1-2 - адиабатное сжатие воздуха в компрессоре;
2-3 - изохорный подвод тепла;
3-4 - адиабатное расширение продуктов сгорания в турбине;
4-1 - изобарный отвод тепла в атмосферу.
9.8. К. п. д. ГТУ с подводом теплоты при постоянном объеме.
t = 1-q2/q1
q1 = Cu(T3-T2) ;
q2 = Cp(T4-T1)
t = 1 - K(T4-T1)/(T3-T2)
 = p2/p1 ;
 = p3/p2 - степень повышения
давления
k-1/k
T4 = T3(1/() ) ;
T3 = T2 ;
T2 = T1k-1/k
t = 1- K(T11/k-T1/T1k-1/k-T1k-1/k) = 1-K(1/k-1/(-1)k-1/k)
t = 1- k(1/k-1)/ k-1/k(-1)
Т. к. п. д. возрастает с ростом К,  и .
ГТУ с подводом тепла при постоянном объеме в настоящее время находятся
в опытных образцов установок ввиду устройства камеры сгорания и низкой
жаропрочности материалов клапанов.
49
Кроме того, для снижения пульсаций давления в трактах компрессора и
турбины необходимо устанавливать ресиверы (большие емкости), снижающие
уровень этих пульсаций.
При равных степенях повышения давления  и равных максимальны
температурах цикла T3 к. п. д. цикла с подводом тепла при постоянном объеме
выше, чем к. п. д. цикла с подводом тепла при постоянном давлении т.к. T2cp изохорн.
< T2cp изобарн.
t изохорн.  t изобарн.
При разных степенях повышение давления  и равных максимальных
температурах цикла T3 к. п. д. цикла с подводом тепла при постоянном давлении
выше, чем к. п. д. цикла с подводом тепла при постоянном объеме вследствие
более высокой средне интегральной температуре подвода тепла, т.е. T1cp изобарн.T1ср
изохорн.
t изобарн.  t изохорн.
9.9. Способы повышения экономичности ГТУ
1. Увеличение степени повышения давления  () целесообразно
осуществлять до разумных пределов, т.к. увеличивается число ступеней
компрессора, а суммарный к. п. д. компрессора падает. Для реальных ГТУ
существует оптимальная степень повышения давления.
В реальных термодинамических циклах, учитывающих к. п. д. компрессора
и к. п. д. турбины термический к. п. д. цикла имеют максимум при определенном
значении степени повышения давления.
Обычно компр. = 0,84 - 0,86 для осевых компрессоров
компр. = 0,8 - 0,82 для центробежных компрессоров
турб. = 0,85 - 0,82
В современных ГТУ используется многоступенчатые, зачастую
многокаскадные (двух - трехкаскадные) осевые компрессоры, имеющие степень
повышения давления до 40-50.
Осевой компрессор является наиболее сложным узлом ГТУ как с точки зрения его
расчета и проектирования, так и с точки зрения сложности производства. Он
потребляет до 80% мощности, развиваемой газовой турбиной. Существует
поговорка среди специалистов ГТУ “Хороший компрессор - хороший двигатель”.
2. Увеличение температуры газа перед турбиной T3 повышает т.к. п.д. ГТУ,
но требует применение специальных дорогостоящих материалов, сложный
системы охлаждения лопаток турбины. Ресурс ГТУ при этом существенно
снижается. В настоящее время для стационарных ГТУ температура T3 не
превышает обычно 1150С.
3. Регенерация теплоты
50
Регенератор представляет собой теплообменный аппарат, в котором тепло
уходящих продуктов сгорания передается воздуху, сжатому в компрессоре.
Регенерация возможна лишь при T4  T2
Для идеального цикла при полной регенерации
t рег. = 1 - T1/T4
q1 = Cp(T3-T5) = Cp(T3-T4) ;
T3 = T4k-1/k
q2 = Cp(T6-T1) = Cp(T2-T1) ;
T2 = T1k-1/k
t = 1 - q2/q1 = 1- (T1k-1/k-T1)/(T4k-1/k-T4) = 1 - T1/T4
Для реального цикла т.к. п.д. всегда меньше, т.к. полную регенерацию
осуществить нельзя вследствие конечной разности температур продуктов
сгорания и подогреваемого воздуха в теплообменнике, а также ограниченных
размеров самого теплообменника.
4. Многоступенчатые сжатие воздуха с промежуточным его охлаждением и
многоступенчатые сгорания топлива.
Сжатый воздух охлаждается в промежуточных холодильниках. Обычно
осуществляют трехкаскадное сжатие воздуха.
При сгорании топлива в камерах сгорания ГТУ коэффициент избытка
воздуха обычно составляет 3 - 5. Поэтому продукты сгорания содержат большое
количество свободного кислорода, который можно использовать для дожигания
топлива в промежуточной камере сгорания.
5. Применение ГТУ замкнутой схемы. В качестве рабочего тела
целесообразно использовать одноатомные газы (К=1,66). Тогда т.к. п.д. выше при
тех же степенях сжатия (повышения давления). Такие схемы представляются
перспективными для ядерных ГТУ.
6. Утилизация тепла уходящих газов ГТУ. Теплоту уходящих газов можно
не пользовать для получения пара и горячей воды.
ГТ25-700 ЛМЗ снабжена сетевым подогревателем, позволяющим получать воду
температурой 150-160С.
7. Использование тепла уходящих газов ГТУ для подогрева воды и
парообразования в паросиловых установках (парогазовый цикл).
Парогазовая установка является бинарной установкой. Пример - эсминец
США “Орли Берх”. Подобные установки используются как в энергетике, так и на
51
транспорте (судовые ГТУ с утилизационными паровыми котлами. Паровая и
газовая турбины работают на общий редуктор)
9.10. Недостатки ГТУ
1. Низкая температура газа перед турбиной, т.е. низкая максимальная
температура цикла ГТУ.
2. Отсутствие компактных теплообменников для регенерации тепла в ГТУ.
3. Определенная сложность регулирования транспортных ГТУ.
4. Малый срок службы по сравнению с паровыми турбинами.
9.11. Газотурбинные
теплогазоснабжения.
установки
в
строительстве,
системах
1. ГТУ применяются в качестве пиковых приводов на электростанциях.
2. Используются на временных электростанциях.
3. ГТУ применяются в качестве приводов компрессоров магистральных
газопроводов. В качестве топлива используется перекачиваемый природный газ. В
качестве привода используются авиационные ГТД, выработавшие свой ресурс.
52
10. ЦИКЛЫ ДВИГАТЕЛЕЙ ВНУТРЕННЕГО СГОРАНИЯ
ПРИНЦИПИАЛЬНАЯ СХЕМА ДВС.
Клапанный механизм связан c кривошипно-шатунным.
Двигатели внутреннего сгорания отличаются от паровых тем, что сгорание
происходит внутри рабочего органа машины.
Первые попытки принадлежали механику Ленуару (Франция). В 1860 г. был
построен двигатель, работавший на светильном газе. К. п. д. был низок – не выше
паровой машины.
В 1862 г. Бо – де – Роша (Франция) запатентовал, а в 1877 г. Отто (Германия)
построил бензиновый двигатель.
Цикл Отто (υ = const)
В термодинамике исследуют не реальные необратимые процессы в ДВС, а
идеальные обратимые циклы. В качестве рабочего тела принимают идеальный газ
с постоянной теплоемкостью. Полагают, что подвод теплоты осуществляется не за
счет сжигания топлива, а от внешних источников теплоты.
0 - 1 – так всасывание (наполнения).
Термодинамическим процессом не является.
Смесеобразование – в карбюраторе.
1 – 2 адиабатное сжатие горючей смеси
 - зажигание смеси от свечи
2 – 3 – изохорный подвод тепла
q1
3 – 4 – адиабатное расширение
4 – 1 – изохорный отвод тепла q2
4 – 0 – такт выпуска (выхлопа)Рис. 17.2а
Нетермодинамический процесс
Т2 = Т1  εк-1
υh – рабочий объем
Т3 = Т1  λ  εк-1
υh = υ1 – υ2
Т4 = Т1  λ

1
 2 - степень сжатия;

3
- степень повышения давления.
2
При анализе циклов считают параметры рабочего тела 1 известными. Тогда
можно определить параметры в точках 2, 3, 4 и выразить их через параметры
точки 1.
53
Т. к. п. д. цикла Отто
q
C (T  T )
T T
1
t  1 2  1 v 4 1  1 4 1  1 k1
q1
Cv (T3  T2 )
T3  T2

1
t  1 k1

Ε
Т. к .п. д. цикла Отто зависит только от рода рабочего тела и степени сжатия.
2
4
6
8
10

ηt
0.25
0.43
0.52
0.57
0.61

К = 1.4
С увеличением степени сжатия темп нарастания ткпд падает, но рост
продолжается, хотя и очень медленно. Рабочее топливо – бензин (легкие моторные
топлива), газ.
1. При повышении степени сжатия возникает преждевременное воспламенение в
цилиндре, что вызывает отрицательную работу и снижение ткпд.
2. Детонация. Скорость сгорания при этом  2000 м/с. При нормальном горении –
20 – 30 м/с. Антидетонаторы дорогие и вредные добавки.
10.1. Цикл Дизеля (р = const)
Разработан в 1897 г. Первый двигатель работал на керосине. Распыления
топлива – компрессором воздушным.
1 – 2 сжатие воздуха (ε – до 20)

3
2
-
степень
предварительного
расширения
3 – 4 – адиабатное расширение
Рис.17.3а
Если провести подсчет ткпд цикла Дизеля по аналогии с подсчетом ткпд
цикла Отто, то получим
 k 1
t  1 k 1 
k( 1)

1
K = 1.41
При одинаковых степенях сжатия ткпд цикла Отто выше ткпд цикла Дизеля.
Для работы дизелей используются тяжелые моторные топлива (соляровое
масло, нефть). Они значительно дешевле, менее опасны в пожарном отношении.
54
Недостатки дизельных двигателей – больший вес, большая стоимость,
шумность, сложность регулирования. Экономичность дизельных двигателей
высокая.
Пока это самые экономичные двигатели
Удельный расход доходит (ве) до 0.18 – 0.2 кг/ кВт  час, ηе – до 40%.
Компрессор требует больших затрат мощности (до 10%).
10.2. Цикл Тринклера (цикл со смешенным подводом тепла)
Запатентован Сабатэ. Первый двигатель в 1893 построил Мамин.

1
4
p3




2 ;
3
p2 ;
Тринклер в 1904 г. построил бес
компрессорный двигатель, работавший по
такому циклу.
Рис. 17.4.а
Топливо распыляется механически при помощи плунжерного насоса и
форсунки при давлениях до 70 мПа
k  1
t  1  k 1 

(  1)  k (   1)
1
Цикл Отто (ρ = 1) и цикла Дизеля (λ = 1) – частные случаи цикла Тринклера.
По этому циклу работают большинство современных двигателей.
10.3. Изображение циклов двигателей внутреннего сгорания в Т – S
координатах.
10.3.1. Цикл Отто, цикл Дизеля
Рис. 17.2б
Рис.17.3б
55
При равных степенях сжатия и равенстве максимальных температур циклов
Т3 цикл Дизеля имеет более низкий к. п. д., чем цикл Отто
ηtизоб < ηtизох
Этот вывод можно получить, сравнивая среднеинтегральные температуры
подвода и отвода тепла в этих циклах
ηtизоб < ηtизох
При разных степенях сжатия и одинаковых максимальных температурах
циклов Т3 цикл Дизеля имеет больший к. п. д. по сравнению с циклом Отто.
10.4. Двухтактные д. в. с.
Основное отличие от четырехтактных состоит в том, что наполнение
цилиндра горючей смесью или чистым воздухом осуществляется в наличии хода
сжатия, а выпуск продуктов сгорания – в конце рабочего хода
Эффективный к. п. д. двухтактных д. в. с. невысок, удельный расход топлива
у них существенно выше, чем у четырехтактных.
Применяются двухтактные д. в. с. в основном при необходимости
достижения малой удельной массы двигателя (мотопилы, мотоциклы, модели и т.
п.)
10.5. Классификация
1. По рабочему циклу – двухтактные и четырехтактные.
2. По способу смесеобразованию – с внешнем и внутренним смесеобразованием.
3. По способу воспламенения – с самовоспламенением от сжатия;
с воспламенением от электрической искры;
с воспламенением от калоризатора;
4. По роду топлива – газовые;
двигатели легкого топлива (бензиновые)
двигатели тяжелого топлива (дизельные)
5. По назначению – стационарные
передвижные
транспортные (авто, авиа, судо, тепловозные)
6. По конструктивному исполнению. Классификация еще более
обширна.
10.6. Применение ДВС в строительстве.
Главным образом 4-х тактные дизели, 4-х тактные карбюраторные
двигатели.
Применение:
1. Привод компрессоров
2. Строительные машины (экскаваторы, бульдозеры, монтажные краны).
3. Временные электростанции – для привода электрогенераторов.
Иногда используется дизель – электрические или дизель – гидравлические
передачи.
На газоперекачивающих станциях применяются ДВС и ГТУ в качестве
приводов на компрессорных станциях перекачки газа. В последние годы
56
используются авиационные ТРД, выработавшие свой летный ресурс. Топливом
служит газ из газопровода.
10.7. Индикаторная диаграмма.
Индикаторная диаграмма – кривая зависимость давления в цилиндре
двигателя от объема рабочего тела.
Среднее индикаторное давление – условное постоянное избыточное
давление, которое, действия на поршень, совершает за один цикл.
Индикаторная мощность двигателя – мощность, развиваемая внутри
цилиндра.
Lу = pi  Vh,
где Vh – рабочий объем цилиндра;
Ni 
pi Vh  i  n
, где i – число цилиндров;
30
n – скорость вращения, об/мин;
i – число цилиндров;
τ = 4 для четырехтактных двигателей;
τ=2 для двухтактных двигателей;
piD 2  H  i  n
Ni 
, где D – диаметр цилиндра;
120 i
H – ход поршня.
Эффективная мощность – мощность отдаваемая потребителю, мощность на
выходном валу двигателя
Ne = Ni  ηм
где
ηм – механическая к. п. д.,
учитывающий потери
на трение и привод
вспомогательных
механизмов.
ηм = 0.7…0.92
10.8. Эффективный КПД и расход топлива.
e 
Ne
mT QHP ,
где
QHP - низшая рабочая теплота
сгорания топлива;
mT – расход топлива, кг/с
Для карбюраторных двигателей ηе = 0.22…0.32
Для дизельных двигателей ηе = 0.32…0.50
ge 
mT
1

Ne eQHP - эффективный расход топлива
[g] = кг/квт  час
QHP  40000 кДж/кг
для нефтяных топлив
Для карбюраторных двигателей ge = 0.27…0.4 кг/кВт  час
Для дизельных двигателей ge = 0.16…0.27 кг/кВт  час
57
10.9. Перспективные направления в развитии д.в.с.
Суммарная мощность всех д.в.с. значительно превышает суммарную
мощность всех электростанций. Они являются одними из главных загрязнителей
окружающей среды.
Карбюраторные д.в.с. выбрасывают в атмосферу окись углерода (СО),
тетроэтилсвинец Рв(С2Н5)4, применяющийся в качестве антидетонатора.
Дизельные двигатели дают выбросы сажи, углеводородов.
И карбюраторные, и дизельные дают выбросы в атмосферу альдегиды,
окислы азота.
В настоящее время проводятся большое количество исследований и работ по
переводу д.в.с. на другие топлива:
1. Газообразные топливо, сжиженные газы;
2. Спирты (особенно в тропических странах);
3. Водород в качестве топлива. Такие исследования ведутся, в частности в
содружестве с институтом проблем машиностроения АН УССР.
58
11. ОСНОВЫ ТЕПЛООБМЕНА.
Теория теплообмена - наука о процессах распространения теплоты в
твердых, жидких и газообразных телах.
Согласно 2 закону термодинамики самопроизвольный процесс переноса
теплоты в пространстве возникает под действием разности температур и
направлен в сторону уменьшения температуры. Закономерности переноса теплоты
и количественные характеристики этого процесса являются предметом
исследования теории теплообмена.
Различают три основных вида (способа) передачи тепла:
теплопроводность; (нагрев стержня)
конвекция; (калориферы)
тепловое излучение; (солнечная энергия)
Теплопроводность - молекулярный перенос теплоты в сплошной среде. Этот
процесс возникает при неравномерном распределении температур в среде.
Перенос теплоты происходит между непосредственно соприкасающимися телами
или частицами тел с различной температурой.
Конвекция - перенос теплоты при перемещении объемов жидкости или
газа в пространстве. Происходит только в газах или жидкостях. При этом перенос
теплоты неразрывно связан с самим переносом среды.
В теории теплообмена, как и в гидромеханике, термином “жидкость”
обозначается любая сплошная среда, обладающая свойством текучести.
Подразделение на “ капельную жидкость” и “газ” осуществляется только в том
случае, когда агрегатное состояние вещества играет в рассматриваемом процессе
существенную роль.
Тепловое
излучение
процесс
распространения
теплоты
с
электромагнитными волнами. При этом внутренняя энергия тела переходит в
энергию излучения, электромагнитные волны распространяются в пространстве,
энергия излучения поглощается другими телами.
Элементарные процессы распространения тепла - теплопроводность,
конвекция и тепловое излучение обычно происходят совместно.
Виды переноса тепла.
Теплопроводность в чистом виде большей частью имеет место лишь в
твердых телах.
Конвекция теплоты всегда сопровождается теплопроводностью. Одновременный
перенос теплоты конвекцией и теплопроводностью называют конвективным
теплообменом.
Теплоотдача (конвективная теплоотдача) - обмен теплом между твердой
поверхностью и жидкостью путем теплопроводности и конвекции.
Радиационно - кондуктивный теплообмен - обмен теплом при передачи его
теплопроводностью и излучением.
Радиационно - конвективный (сложный) теплообмен - передача теплоты
конвекцией, теплопроводностью и излучением - совокупность всех трех видов
переноса теплоты.
59
Теплопередача - процесс теплообмена
теплоносителями, разделенными твердой стенкой.
между
двумя
жидкими
11.1. Теплопроводность.
Металлах основной передатчик теплоты - свободные электроны. В
диэлектриках и жидкостях тепло передается путем упругих волн. В металлах
влияние колебаний является второстепенным по сравнению с переносом энергии
путем диффузии свободных электронов.
В газах перенос энергии обусловлен диффузией молекул и атомов.
Т.о. теплопроводность обусловлена движением микрочастиц вещества.
В жидкостях и газах чистая теплопроводность может быть реализована
только при отсутствии переноса тепла конвекцией.
Температурное поле.
Температурное поле - совокупность температур всех точек исследуемого
пространства в каждый момент времени.
t = t (x,y,z,) - этим уравнением описывается
температурное поле в общем виде.
Температура изменяется как от одной точки к другой, так и во времени.
Такое поле называется нестационарным.
Если температура в каждой точке поля не изменяется во времени, то такое
поле называется стационарным.
Поля могут быть трех-, двух- и однокамерными, причем как стационарными,
так и нестационарными.
Двухмерные
t = t(x,y,); t/z=0
t = t(x,y); t/z=0
Одномерное
t = t(x,); t/z=0
t = t(x); t/z=0;
Этими уравнениями описываются двухмерные и одномерные поля.
Температурный градиент.
Изотермическая поверхность - геометрическое место точек с равными
температурами.
Т.к. одна точка не может иметь двух температур, то изотермические
поверхности никогда не пересекаются друг с другом. Замыкаются сами на себя
или обрываются на границах тела.
Изотерма - линия пересечения изометрической
поверхности с плоскостью. Изотермы также никогда
не пересекаются друг с другом.
На рисунке изображены две изотермы,
температуры которых отличаются на t
t/n t/x т.к. nx
60
Т.к. температура вдоль изотермической поверхности или изотермы не
изменяется, то для ее изменения следует двигаться в направлениях, пересекающих
изотермические поверхности.
Наибольший перепад на единицу длины происходит по направлению
нормали к изотерме.
Градиент температуры - вектор, направленный по нормали к
изотермической поверхности в сторону возрастания температуры и равный
производной температуры по направлению
grad t = nt/n ; n - единичный вектор
В проекциях
(grad t)x = t/x
(grad t)y = t/y
(grad t)z = t/z
Поскольку n = 1, то t/n
также называют температурным
[grad t] = K/M = C/M
градиентом.
Тепловой поток
Тепловой поток - количество тепла, переносимое через какую-либо
поверхность в единицу времени.
Удельный тепловой поток* (плотность теплового
потока) - количество тепла, переносимое через единицу
площади изотермической поверхности в единицу
времени
Удельный тепловой поток также является
векторной величиной* , направлен по нормали к
изотермической поверхности в сторону убывания
температуры
Закон Фурье.*
Основной закон теплопроводности (закон Фурье) гласит, что количество
теплоты,
проходящее
через
элемент
изотермической
поверхности,
пропорционально градиенту температуры и продолжительности промежутка
времени.
Коэффициент теплопроводности.
Является теплофизической характеристикой материала.
[  ] = [q]/[grad t] = Вт/м2 к/м = Вт/мК
Коэффициент теплопроводности численно равен количеству теплоты,
проходящей через единицу изотермической поверхности в единицу времени при
единичном градиенте температуры.
В общем случае  = (t).
61
Для многих материалов его зависимость от температуры определяется по
формуле
 = [ 1+b(t-t) ]
1. Металлы.
= 3 ÷ 458 Вт/м· К
С увеличением температуры  убывает. Коэффициент тепло- и
электропроводности у металлов пропорциональны, т.к. носители тепловой энергии
и заряда одни и те же - электроны.
Для сплавов коэффициент теплопроводности ниже, чем для чистых
металлов. С увеличением температуры  растет.
2. Неметаллы.
 = 0,02  3 Вт/мК
Обычно с увеличением температуры  растет.
Многие строительные и теплоизоляционные материалы имеют пористую
структуру. Для них  - условная величина, которая имеет смысл коэффициента
теплопроводности “эквивалентного сплошного материала”.
Материалы с   0,25 Вт/мК называются теплоизоляционными.
Жидкости.
 = 0,08  0,65 Вт/мК
С увеличением температуры  убывает (за исключением воды).
4. Газы.
 = 0,005  0,6 Вт/мК
С увеличением температуры растет (и довольно существенно)
Краевые условия.
Дифференциальное уравнение Фурье описывает явление теплопроводности
в самом общем виде. Применение его в конкретных случаях требует знания
распределения температур в теле в начальный момент времени (начальные
условия). Кроме того, должны быть известны физические параметры среды и тела
и распределение температур на поверхности тела (граничные условия).
Граничные условия могут быть заданы тремя способами.
1.Граничные условия 1 рода.
Задается распределение температуры на поверхности тела для каждого
момента времени.
tc = tc(x,y,z,).
2. Граничные условия 2 рода.
Задается поверхностная плотность теплового потока в каждой точке
поверхности тела в любой момент времени.
qn = qn (x,y,z,).
3. Граничные условия 3 рода.
Задается температура среды, окружающей тело, и закон теплообмена между
поверхностью тела и окружающей средой.
При конвективном теплообмене используется закон Ньютона -Рихмана.
q = ( tc - tж ), где  - коэффициент теплоотдачи
Количество теплоты, отдаваемой единицей поверхности тела в единицу
времени, пропорционально разности температур поверхности тела и окружающей
среды.
[] = Вт/м2к
62
Коэффициент теплоотдачи численно равен количеству теплоты,
отдаваемому (или воспринимаемому) единицей поверхности в единицу времени
при разности температур поверхности и окружающей среды в 1 К.
Теплопроводность через однослойную плоскую стенку
Процесс рассматривается при стационарном режиме, при отсутствии
внутренних источников тепла.
1.
t/ = 0 ;
 = Const - однородный изотропный
qu = 0 ;
t/y = 0 ; t/z = 0
материал
Тогда дифференциальное уравнение принимает вид :
2t/x2 = 0 ;
d2t/dx2 = 0 ;
dt/dx = C1 ;
t = C1x+C2
t = t1 ;
x=0
t = t2.
x=
граничные условия 1 рода.
Отсюда
C2 = t1 ; C1 = t2 - t1/
Тогда
t = t1 - t1 - t2/  x
Температура в однородной плоской стенке изменяется по линейному закону.
(grad t) = t/t = - t1 - t2/;
q = - grad t = /(t1 - t2) - получено из уравнения Фурье.
Отсюда :
Q = qF = /(t1 - t2)F - общее количество теплоты, переданной через
поверхность F за время .
Т.к. q/ = t1 - t2/, то
t = t1 - q/x
2. Теперь рассмотрим случай, когда  = (t)
Если  = (1 + bt), то закон Фурье принимает вид
q = -dt/dx = -(1 + bt)dt/dx.
Разделяем переменные
qdx = -(1 + bt)dt ;
qx = -(t + bt2/2) + C.
t = t1
x=0
t = t2 Граничные условия 1 рода. О = -(1+bt12/2)+C
(1)
2
x=
q=-(1+bt2 /2)+C
(2)
63
Отсюда вычитая из (2) уравнение (1)
q = o/1+bt1+t2/2](t1-t2)
Величина [1+bt1+t2/2] = ср - среднеинтегральный коэффициент
теплопроводности.
Тогда q = ср/(t1-t2)
Тепловой поток определяется разностью температур, которую называют
температурным напором.
t = t1 -t2
Теплопроводность многослойной плоской стенки
Считаем, что все слои плотно прилегают
друг к другу
1 = Const
2 = Const
3 = Const
Тепловые потоки для каждого из слоев равны т.к. q/x = 0
Q = 1/1F(t1-t2)
t1- t2 = Q/F1/1
Q = 2/2F(t2-t3)
t2- t3 = Q/F2/2 +
Q = 3/3F(t3-t4)
t3- t4 = Q/F3/3
t1 - t4 = Q/F(1/1+2/2+3/3)
q - Q/F = t1 - t4/(1/1+2/2+3/3)
Для n слоев
q = t1-tn+1/(ni=1i/i)
Отношение / называется тепловой проводимостью стенки
[/] = Вт/м2К.
Отношение / называется термическим сопротивлением стенки
[/] = м2К/Вт.
Rc = / - термическое сопротивление теплопроводности.
Температура в каждом слое стенки изменяется по линейному закону.
Температурный график для многослойной плоской стенки - ломаная линия.
Иногда выражение Q = Ft/(ni=1i/i) называют законом Ома для тепловой
цепи.
Сравнение : І = U/(ni=1Ri) = SU/(ni=1L/)
Иногда вводится понятие эквивалентной теплопроводности. При этом
полагают
ni=1i =  ;
ni=1i/i = /жв.
64
Отсюда жв. = ni=1i/ni=1 (i/i) - эквивалентный коэффициент
теплопроводности.
Теплопроводность цилиндрической стенки.
Считаем, что температура изменяется только в радиальном направлении, т.е.
t = t(r) ;  = Const
Тогда тепловой поток через участок кольцевого слоя трубы длиной L
составит
Q = -2rL  dt/dr.
Разделяя переменные получим
dt = - Q/2L  dr/r
t = -Q/2L Lnr+C
- уже отсюда видно, что температура
внутри стенки изменяется по
логарифмическому закону.
Полагая
t/r=r1 = t1i
t/r=r2 = t2i Граничные условия 1 рода.
Получим t1-t2 =Q/2LLnr2/r1
Q = (t1-t2)/Lnr2/r12L; qL= Q/L
Тепловой поток на единицу длины цилиндра
qL = (t1-t2)/(1/2Lnr2/r1)
Температура внутри стенки изменяется по логарифмической кривой. Это
объясняется тем, что плотность теплового потока изменяется с изменением
радиуса.
Многослойная цилиндрическая стенка.
Стенка состоит из плотно прилегающих цилиндрических слоев. i = Const
Для каждого слоя
qL = (t1-t2)/(1/21Lnr2/r1);t1- t2=qL/21Lnr2/r1
qL = (t2-t3)/(1/22Lnr3/r2);t2- t3=qL/22Lnr3/r2
qL = (t4-t3)/(1/22Lnr4/r3);t4-t3=qL/23Lnr4/r3
Тогда
65
t1-t4=(qL/2)(1/1Lnr2/r1+1/2Lnr3/r2+1/3Lnr4/r3
qL=(2(t1-t4))/(1/1Lnr2/r1+1/2Lnr3/r2+1/3Lnr4/r3
В общем случае
Q = (2L(t1-tn+1))/(ni=11/iLnri+1/r1
Теплопроводность тел произвольной формы.
Количество теплоты, проходящее через стенки тел неправильной формы,
можно определить по уравнению
Q = /Fcp(t1-t2),
где Аср - поверхность, которую находят в зависимости от формы тела.
1.
Плоская стенка
Fcp = (F1+F2)/2.
цилиндрическая (F2/F12)
2.
Цилиндрическая стенка
Fср = (F2-F1)/(LnA2/A1).
3.
Сферическая стенка
Fср = F1F2.
Если температура стенки в отдельных местах различна, то среднюю
расчетную температуру определяют по формуле
tср = 1/FtdF  (ni=1tiFi)/(ni=1Fi), где F = ni=1Fi.
66
12. КОНВЕКТИВНЫЙ ТЕПЛООБМЕН
Основные понятия и определения.
Конвекция теплоты - перенос тепла перемещением в пространстве жидкости
или газа из области с одной температурой в область с другой температурой.
Перенос теплоты при конвекции сопровождается переносом среды, т.е.
массообменом.
Теплоотдача - конвективный перенос теплоты между твердой стенкой и
омывающей ее жидкостью.
Согласно закону Ньютона - Рихмана удельный тепловой поток от стенки к
жидкости пропорционален разности температур между стенкой и жидкостью:
q=(tСТ-tСЖ)
Соответственно для стенки площадью F:
Q=F(tСТ-tСЖ)
Уравнение Ньютона - Рихмана весьма удобно для расчетов, однако основная
сложность заключается в трудности определения коэффициента теплоотдачи .
Коэффициент
теплоотдачи
численно
равен
количеству
теплоты,
переносимому через единицу поверхности стенки в единицу времени при
разности температур между стенкой и жидкостью 1 К.
  
вт
м К
2
Коэффициент теплоотдачи в общем случае зависит от многих факторов и
параметров движения.
=(, , , , tЖ, tСТ, l1, l 2, l 3, Ф...)
l 3 - характерные размеры тел;
Ф - форма тела.
Дифференциальные уравнения конвективного теплообмена.
В общем случае задачи конвективного теплообмена сводятся к решению
следующих дифференциальных уравнений:
1. Дифференциальное уравнение теплопроводности
t
   2 t  2 t  2t 





 c  x 2 y 2 z 2 
или
t
 a 2 t

2. Уравнение Навье-Стокса
67
WX WX
W X
WX
1 p

WX 
WY 
WZ  g 
  2WX

x
y
z
 x
WX
- характеризует нестационарность процесса;

g - массовая сила;
WX
W X
WX
WX 
WY 
W - сила инерции;
x
y
z Z
- для WX
 2WX - сила вязкости;
1 p
- сила давления.
 x
Для идеальной жидкости силы вязкости отсутствуют. Уравнение Навье-Стакса
упрощается уравнениями Эйлера.
3. Уравнение неразрывности.


 div    0

Для несжимаемой жидкости в стационарном процессе
Wx Wy Wz


x
y
z
4. Уравнение конвективного теплообмена
t
t
t
t

 Wx
 Wy
 Wz

 2t
c


x
y
z
Это уравнение называют уравнением Фурье-Кирхгофа.
Если W= 0, то уравнение принимает вид дифференциального уравнения
теплопроводности.
5. Уравнение теплоотдачи.

q
tст - tж
Для тонкого слоя жидкости вблизи стенки
 t 
q    
 n  n 0 - по закону Фурье
Отсюда :
  t 

 
- уравнение теплоотдачи
tст  tж  n  n0
Помимо этих уравнений необходимо ввести определенные краевые условия.
Аналитическое
решение
системы
дифференциальных
уравнений
конвективного теплообмена получено лишь два ряда ограниченного числа задач.
68
Для расчета сложных процессов используют результаты экспериментальных
исследований и теорию подобия.
12.2 Факторы, влияющие на интенсивность конвективного
теплообмена.
1. Свободная и вынужденная конвекция.
По природе возникновения различают два вида движения - свободное и
вынужденное. Свободное движение происходит вследствие разности плотностей
нагретых и холодных частиц жидкости, находящихся в поле действия сил тяжести;
оно называется также естественной конвекцией и зависит от рода жидкости,
разности температур, объема пространства, в котором протекает процесс.
Вынужденное движение возникает под действием посторонних побудителей
(насоса, вентилятора, ветра). В общем случае наряду с вынужденным движением
одновременно может развиваться и свободное.
2. Ламинарное и турбулентное движение.
Движение жидкости может быть ламинарным или турбулентным. При
ламинарном режиме частицы жидкости движутся послойно, не перемешиваясь.
Турбулентный режим характеризуется непрерывным перемешиванием всех слоев
жидкости. Переход ламинарного режима в турбулентный п\определяется
критическим значением безразмерного комплекса, называемого числом
Райнольдса:
l
Re к р
,

где w - скорость движения жидкости; v - коэффициент кинематической вязкости; l
- характерный размер канала или обтекаемой стенки.
12.3. Основы теории подобия.
С понятием подобия исследователи сталкиваются не только в математике, но
и в других областях наук.
Геометрически подобные фигуры обладают тем свойством, что их
соответственные углы равны, а сходственные стороны пропорциональны.
l1'
l1
''
l1/ /
 Cl - коэффициент пропорциональности
l1/
(постоянная геометрического
подобия)
На основании свойств подобия можно решить ряд задач (определение
расстояния до цели, до небесных тел и т.п.)
Понятие подобия можно распространить на любые физические явления.
69
При этом следует руководствоваться следующими положениями:
1. Понятие подобия применимо только к физическим явлениям одного и того
же рода. Эти явления должны описываться одинаковыми уравнениями как по
форме, так и по содержанию.
Емкость
Теплопроводность
Электропроводность
Диффузия
Эти явления аналогичные,
а не подобные!
2. Обязательным условием является геометрическое подобие.
3. При анализе можно сопоставлять только однородные величины в
сходственных точках в сходственные моменты времени.
Однородные величины имеют одинаковый физический смысл и одну и ту же
размерность.
4. Подобие явлений означает подобие всех величин, характеризующих эти
явления.
'' = С'
C - постоянная подобия.
12.4. Теоремы подобия.
Постоянные подобия для различных величин в подобных явлениях нельзя
выбирать произвольно. Соотношения между ними выводятся из уравнений,
описывающих процессы.
Соотношения постоянных подобия устанавливают существующие критериев
подобия, которые для всех подобных явлений сохраняют одни и те же числовые
значения.
Критерии подобия - безразмерные комплексы, составленные из величин,
характеризующих явление.
Основные положения теории подобия формулируются в виде трех теорем:
. Подобные между собой процессы имеют одинаковые критерии подобия.
. Решение дифференциального уравнения может быть представлено в виде
связи между критериями, вытекающими из этого уравнения.
Такое уравнение называется критериальным.
. Подобны те процессы, условия однозначности которых подобны, и критерии,
составленные из величин, входящих в условия однозначности, одинаковы.
Третья теорема фактически определяет условия, необходимые и достаточные
для подобия процессов.
Критерии, состоящие только из величин, входящих в условия однозначности,
называются определяющими.
Переменные, имеющие вид критериев подобия, вычисляемые в процессе
решения задачи, называются определяющими.
70
12.5. Числа подобия, их физический смысл.
1.
Eu 
p
- число Эйлера
W 2
Выражает соотношение между силой давления и силой инерции в
рассматриваемо явлении.
Wl
W 2
2. R e   
W - число Рейнольдса

l
Выражает соотношение между силой инерции и силой внутреннего трения.
3. Nu 
l T    l



T  
qст
T 

l

qст
qст 
Характеризует соотношение между конвективным переносом тепла и
переносом тепла теплопроводностью через слой толщиной l.
4. Pz 
C P
 
 CP  
a 

- число Прандтля.
Теплофизическая характеристика теплоносителя.
5. P e  R e  P z
Wl
- число Пекле.
a
Выражает соотношение между интенсивностью процесса теплоты конвекцией
и интенсивностью переноса теплоты теплопроводностью.
6.
l3
Gr  g t 2

- число Грасгофа. Для газов  
1
T
Выражает относительную эффективность подъемной силы.
gl 3 
7. Ar  2 


- число Архимеда.
Характеризует отношение подъемных сил к силам вязкости.
При свободной конвекции уравнение подобия для процессов теплообмена
имеет вид:
Nu=f(Gr,Pr)
При совместном свободно-вынужденном движении теплоносителя уравнение
подобия приобретает вид:
Nu=f(Re,Gr,Pr)
71
Если влияние свободной конвекции невелико, то уравнение подобия имеет
вид:
Nu=f(Re,Pr)
Теплоотдача при вынужденном движении жидкости в трубах.
Характер движения жидкости в трубах может быть ламинарным и
турбулентным. О режиме течения судят по величине числа Рейнольдса
(характерный размер - диаметр трубы).
Если Re < 2000, то режим движения считают ламинарным.
Обычно полагают, что при движении жидкости в трубах критическое число
Рейнольдса составляет 2000 (по некоторым книгам - 2320).
В диапазоне 2000 < Re > 104 течение называют переход1ным. Развитое
турбулентное течение в трубах устанавливается при Re > 104.
Формирование характера потока происходит в начальном участке. При входе
в трубу скорости распределяются равномерно.
В дальнейшем вдоль стенок трубы образуется пограничный слой, который
становится в конце концов равным радиусу трубы. В трубе устанавливается
постоянное распределение скоростей по радиусу. Наступает стабилизированное
течение.
Длина участка стабилизации равна ~ 50d.
Коэффициент теплоотдачи имеет максимальное значение у входа в трубу,
затем резко убывает, далее стремится к неизменному значению.

лок

l
Длина участка
тепловой
стабилизации
72
Температурный напор вдоль трубы изменяется
t
t'm
t'
t'm
tc
t
t /  t / /
t лог 
t /
ln / /
t
''
l
12.7. Расчетные уравнения.
1. Для ламинарного движения (вязкостный режим).
Nu ж  0,15 Re
0 , 33
ж
Pr
0 , 43
ж
 Prж 


 Prст 
0 , 25
Nu ж  0,13 Re 0ж,33
- для воздуха
Для коротких труб (l<50d) вводится поправочный коэффициент к .
1
5
10
20
1,9 1,44 1,28 1,13
l
2. Для вязкостно-гравитационного режима:
ld
 Pr 
Nu ж  0,15 Re 0ж,33 Prж0,43  ж 
 Prст 
40
1,02
0 , 25
 Grж0,1
Nu ж  0,13 Re 0ж, 33 Grж0,1 - для воздуха
Grж0,1 - учитывает естественную конвекцию.
3. Для турбулентного режима:
Nu ж  0,21 Re
0 ,8
ж
Pr
0 , 43
ж
 Prж 


 Prст 
0 , 25
при Re ж  10 4
0,6 < Prж  2500
Для воздуха (Pr=0,71)
Nu ж  0,018 Re 0ж,8
При движении в изогнутых каналах вводится поправка в значение
полученного коэффициента теплоотдачи:
d
 R  1  1,77 , где R - радиус змеевика
R
d - диаметр трубы
73
12.8. Теплоотдача при поперечном омывании труб и пучков труб.
Обтекание одиночной трубы.
Опытным путем установлено, что при поперечном обтекании цилиндра
ламинарное безотрывное течение возможно лишь при малых числах Рейнольдса.
Такое имеет место только при Re<5; Re 
w0 d

При Re < 5 цилиндр представляет собой плохообтекаемое тело. На передней
части образуется пограничный слой, в кормовой части отрываются от поверхности
цилиндра симметричные вихри. С увеличением скорости вихри начинают
вытягиваться по потоку, затем происходит отрыв . Образуется вихревая дорожка
(дорожка Кармана).
Давление в кормовой части цилиндра
увеличивается с уменьшением местной
скорости. Это приводит к образованию
возвратного движения вблизи поверх-
Возвратное течение оттесняет
пограничный слой от поверхности тела и вызывает отрыв потока
74
Отрыв ламинарного пограничного слоя имеет место при малых числах
Реейнольдса и малой степени турбулентности набегающего потока. Отрыв
происходит при величине угла 82 (см.рис.19.4).
Отрыв турбулентного пограничного слоя происходит при величине угла
140. Это приводит к уменьшению вихревой зоны срыва за цилиндром.
Экспериментально установлено, что при Re = (1÷4)105 течение в значительной
части периметра в пограничном слое становится турбулентным. Турбулентный
пограничный слой более устойчив.
Своеобразная картина обтекания трубы отражается на теплоотдаче.
Интенсивность теплоотдачи по окружности трубы неодинакова.


0.5
 1,6 при =0
 0,35 при =95
 1
при =180
1.0
0.5
Коэффициент теплоотдачи максимален в передней критической точке,
убывает по мере утолщения пограничного слоя. В кормовой части он возрастает за
счет увеличения интенсивности перемешивания.
Полный теоретический расчет распределения теплоотдачи по окружности
трубы, включая зону отрыва, в настоящее время отсутствует.
12.9. Расчетные уравнения.
Позволяют определять средний по периметру коэффициент теплоотдачи для
трубы.
При Reдж < 103
Для воздуха:
Nu ж  0,56 Re
0 , 50
ж
Pr
0 , 36
ж
 Prж 


 Prст 
0 , 25
Nu ж = 0,49Re 0,50
ж
При Reдж > 103
Для воздуха:
 Pr 
Nu ж  0,28 Re 0ж,60 Prж0 ,36  ж 
 Prст 
0 , 25
Nu ж = 0,245Re 0,60
ж
Эти соотношения справедливы лишь для расчета обтекания труб,
установленных перпендикулярно потоку. Если трубы установлены под углом, то в
расчетных коэффициент теплоотдачи вводится поправка .
75
Тогда
=·=90

1
0.5
90
70
50
30
 , град
10
Существует приближенная формула:
1-0,54cos2
(30°<<90°)
Если =0, то имеет место продольное омывание трубы.
При прочих равных условиях поперечное омываание трубы дает ьолее
высокую теплоотдачу.
12.10. Поперечное омывание пучков труб.
В технике встречаются обычно два вида пучков - шахматный и коридорный.
d
х2
d
х1
Ряды 1 2
3 4
5
х1
Ряды
1
2
3
4
5
Рис.19.5.
x1 - поперечный шаг;
x1 x 2
;
- относительные шаги.
d
d
х2 - продольный шаг;
Характер движения жидкости в пучке и омывания трубок зависит от скорости
жидкости и компоновки пучка.
В коридорных пучках все трубки второго и более рядов находятся в вихревой
зоне впереди стоящих труб. Меду трубками образуются застойные зоны. Лобовая
и кормовая части трубы омываются с меньшей интенсивностью, чем те же части
для одиночной трубы (или первого ряда).
В шахматных пучках практически все трубки омываются одинаково.
На основании опытных результатов установлено:
1. Теплоотдача труб первого ряда определяется начальной турбулентностью
потока.
2. В глубинных рядах (начиная с третьего) теплоотдача определяется
компоновкой пучка и на зависит от степени турбулентности.
3. При малой степени турбулентности набегающего потока теплоотдача двух
первых рядов труб меньше, чем теплоотдача глубинных рядов.
Эмпирические критериальные уравнения получены для трубок глубинных
рядов, полагая, что
76
3=4=5=...=n
12.11. Расчетные уравнения для 3.
Коридорный пучок
Re<103
Nu ж  0,56 Re
0 ,50
ж
0 , 36
ж
Pr
 Prж 


 Prст 
Шахматный пучок.
0 , 25
Для воздуха Nu ж = 0,49Re 0,50
ж
;
Уравнение является единым для обоих типов пучков
Re>103
Nuж  0,22 Re
0 , 65
ж
0 , 36
ж
Pr
 Prж 


 Prст 
0 , 25
Nu ж  0,40 Re
Для воздуха Nu ж = 0,194Re 0,65
ж
0 , 60
ж
Pr
0 , 36
ж
 Prж 


 Prст 
0 , 25
Для воздуха Nu ж = 0,35Re 0,60
ж
1=0,63
2=0,93
1=0,63
2=0,73
Re>2·103
 Pr 
Nuж  0,21Re 0ж,84 Prж0,36  ж 
 Prст 
0 , 25
В ламинарной области теплоотдача шахматных пучков в 1.5 раза выше, чем
коридорных. При числах Райнольдса выше 105 эта разница практически исчезает.
Для n рядов средний коэффициент теплоотдачи определяется по формуле (при
равных площадях теплоотдачи в каждом ряду):

 1   2  ( n  2 ) 3
n
1

Угол наклона пучка труб к направлению потока учитывается коэффициентом .
       90
90
70
77
50
30 20

12.12. Естественная конвекция у горизонтальных труб.
Для труб малого диаметра восходящий
поток сохраняет ламинарный режим
даже вдали от трубы.
Для труб большого диаметра переход
турбулентный режим может происходить в пределах поверхности самой тру
бы.
Средний коэффициент теплоотдачи при свободном ламинарном движении
определяется из уравнения.
Nu dж  0,50( Grdж Prж )
0 , 25
 Pr ж 


 Prс 
0 , 25
Эта же формула применяется для определения коэффициента теплоотдачи
горизонтальных поверхностей.
12.13. Особенности.
1. Если нагретая поверхность обращена кверху, то коэффициент теплоотдачи
увеличивают на 30%, если книзу, то уменьшают на 30%!
2. За определяющий размер принимается меньшая сторона плиты.
Для воздуха Nu dж  0,46Gr 0,25
dж
12.14. Теплоотдача в ограниченном пространстве.
В ограниченном пространстве явления нагрева и охлаждения протекают
вблизи друг друга, разделить их невлзможно, поэтому процесс необходимо
рассматривать в целом.
1. Горизонтальные щели
tc
tc  tc
1
1

tc
1
Слоистая структура.
Устойчивая стратификация.
tc
2
tc
2
tc tc 
1
2
2
t c1  t c2
tc1  tc2
78
2. Вертикальные щели.
Если толщина мала, то вследствие
взаимных помех возникают внутренние
циркуляционные контуры высотой h.
Для тонких щелей перенос тепла вычисляется по уравнениям
теплопроводности.
tc
tc
1
2
12.15. Теплоотдача у вертикальных поверхностей.
Возникающее свободное движение у вертикальных поверхностей может быть
как ламинарным, так и турбулентным. Вначале толщина нагретого слоя мала и
течение жидкости имеет струйный, ламинарный характер. Толщина слоя по
направлению движения увеличивается и при некотором ее значении движение
становится локонообразным, а затем турбулентным.
Особенности:

1. При малых значениях температурного
напора вдоль всей поверхности наблюдается лишь ламинарное движение.
2. При ламинарном движении коэффициент теплоотдачи убывает по мере
увеличения толщины слоя, а при турбулентном - сначала возрастает, а затем
остается постоянным по высоте.
3. В режиме свободного движения
форма играет второстепенную роль.
Основное значение приобретает
протяженность поверхности, вдоль
которой происходит движение.
Рис.19.1
79
Эмпирические уравнения подобия были получены на основании
многочисленных экспериментов с пластинами, трубами и т.п.
Средний коэффициент теплоотдачи для вертикальных труб, пластин,
определяется из уравнений.
 Pr 
Nu жl  0,75( Grжl Pr ж ) 0,25  ж 
 Prст 
0 , 25
- ламинарный режим
при
 Pr 
Nu жl  0,15( Grжl Prж ) 0, 33  ж 
 Prст 
103<GrжlPrж<109
0 , 25
- турбулентный режим
при GrжlPrж>109
В качестве определяющей температуры принята температура окружающей
среды, в качестве определяющего размера - высота трубы или пластины.
Для воздуха Nu жl  0,695Cr 0, 25 и Nu жl  0,133Gr 0,25
жl
жl
12.16. Теплоотдача при свободном движении жидкости.
Свободное движение жидкости возникает за счет неоднородностей массовых
(объемных) сил в этой жидкости. К таким силам относят силы гравитации,
центробежные, электростатические и т.п. Наиболее хорошо исследовано движение
жидкости в поле сил гравитации.
При изменении температуры жидкости неизбежно происходит изменение ее
плотности, что вызывает появление разности гравитационных сил (архимедовых
сил). Т.к. при нагреве жидкости ее плотность обычно уменьшается, то нагретая
жидкость движется вверх в поле сил тяжести, и наоборот.
Т.к. в подобных случаях движение воздуха возникает без внешнего
побуждения, т.е. в результате самого процесса теплообмена, то оно называется
естественной конвекцией.
Свободная конвекция имеет место у нагретых стен, печей, радиаторов систем
отопления, в холодильных установках и т.п.
80
13. ТЕПЛООБМЕН ПРИ ФАЗОВЫХ ПРЕВРАЩЕНИЯХ
13.1. Пленочная и капельная конденсация
Конденсация представляет собой процесс перехода пара или газа в жидкое
(твердое) состояние. Процесс конденсации возможен только при докритическом
состоянии пара или газа. Этот процесс может быть осуществлен либо сжатием,
либо охлаждением пара. Он всегда связан с отводом теплоты.
Конденсация может происходить как в объеме пара, так и на охлаждаемой
поверхности теплообмена.
На практике процесс конденсации встречается в:
1) конденсаторах паровых турбин;
2) теплообменниках холодильных установок;
3) пароводяных теплообменных аппаратах;
4) опреснителях, устройствах для перегонки жидкостей в
химической промышленности и т.п.
Число факторов, влияющих на процесс передачи тепла при конденсации,
значительно больше, чем в случаях теплообмена без измерения агрегатного
состояния. Так, например, при конденсации важное значение имеют физикохимические свойства поверхности тела, причем в сочетании с физикохимическими свойствами самой среды. Учет всех этих факторов является очень
трудным, как в теоретическом, так и экспериментальном плане.
В энергетике, других областях техники чаще встречается конденсация пара
на охлаждаемых поверхностях теплообмена. Конденсация пара на твердой
поверхности теплообмена происходит в том случае, когда температура этой
поверхности меньше температуры насыщения при данном давлении, т.е.
tст  tн
На поверхности стенки при конденсации, образуется либо пленка, либо
капли конденсатора, т.е. в данном случае мы имеем дело не только с
теплообменом, но и массообменом.
Если жидкая конденсированная фаза образуется на поверхности в виде
устойчивой пленки, то такая конденсация называется - пленочной, если в виде
отдельных капель - капельной.
Пленочная конденсация имеет место в случае смачивания поверхности
конденсатом, капельная - в случае не смачивания. Капельная конденсация явление более предпочтительное. Для водяного пара, например, капельная
конденсация может быть в том случае, если поверхность теплообмена покрыта
каким-либо жиром, маслом, топливом.
Коэффициент теплоотдачи при капельной конденсации примерно на
порядок выше, чем при пленочной. Однако для водяного пара капельная
конденсация
- неустойчивое явление, т.к. жировая или масляная пленка
смывается. Для ртути, например, капельная конденсация является основным
видом (в бинарных установках).
При капельной конденсации пар соприкасается непосредственно со стенкой,
в то время как при пленочной образуется пленка конденсата является
дополнительным термическим сопротивлением. Для организации капельной
81
конденсации на стенку наносят специальные вещества (Иногда их вводят в пар).
Коэффициенты теплоотдачи при капельной и пленочной конденсации
весьма велики. Сравнение по .
Порядок
Естественная конвекция в газах 5-30
101
в воде 100-1000
102,5
Вытриденная конвекция в газе
10-500
102
в воде 500-10000
103,5
Пленочная конденсация водяного 4000-15000
104
пара
Капельная
40000-120000 105
В практике в основном встречается пленочная конденсация.
13.2. Основы теплоотдачи при пленочной конденсации.
При пленочной конденсации все тепло, выделяющееся на внешней границе
пленки, отводится к поверхности охлаждения.
На рис. 9.3 представлена схема
пленочной конденсации на вертикальной
стене при ламинарном движении пленки
конденсата.
Впервые коэффициент теплоотдачи
при таком режиме течения пленки
теоретически был определен Нуссельтом
в 1916г. При этом были выдвинуты
следующие предложения:
1. Течение в пленке ламинарное;
2. Сила тяжести уравновешивается силой вязкости;
3. Температура поверхности пленки равна температуре насыщения пара;
4. Тепло передается только поперек пленки и только теплопроводностью;
5. Физические параметры конденсата постоянны по толщине пленки.
Рассмотрев силы, действующие на элементарный объем, тепло,
передаваемое через этот объем, Нуссельт получил среднее значение для
коэффициента теплоотдачи
 = 0,943 4gk3kr/kx(tн - tcт)
если   
x - высота стенки
  4x Изменение этих параметров
показано на рис. 9.4.
  41/x несколько утрировано (не в
масштабе). Выражение справедливо также для
вертикальных труб.
Эти решения являются приближенными,
однако основные закономерности отражены
правильно.
82
Уменьшение коэффициента теплоотдачи объясняется увеличением толщины
пленки.
В конце 40х годов академик Капица П. Л. показал, что более устойчивым
является волновое течение конденсатных пленок, которое одновременно
несколько повышает коэффициент теплоотдачи. Поэтому для практических
расчетов применяют следующую формулу
верт. = 1,14 4gк3кr/к h(tн - tст) , где h - высота стенки,
высота трубы.
Для наклонных труб и стенок в расчетное значение коэффициента
теплоотдачи вводится поправка
=верт4lin
С увеличением температурного напора и высоты стены может возникнуть
турбулентный режим течения пленки. Коэффициент теплоотдачи при
турбулентном движении, естественно, возрастает. Существует ряд формул и для
турбулентного движения (для водного пара-помограммы).
Для горизонтальных труб Нуссельтом получено соотношение
гор. = 0,728 4g к 3к r / к d (tн - tст) ,
где d - диаметр трубы.
Приведенные формулы справедливы для случая конденсации чистого пара
на чистой поверхности. При расчетах и проектировании необходимо учитывать
ряд факторов, влияющих на теплоотдачу.
При расчетах капельной конденсации водяного пара также пользуются
помограммами (Михеев, Исаченко)
13.3. Факторы, влияющие на теплоотдачу при конденсации.
1. Перегрев пара.
Учитывается теплотой перегрева qп. В формулы вместо r подставляют r +
qп.
2. Шероховатость поверхности.
Шероховатость увеличивает толщину пленки и, соответственно, снижает
теплоотдачу.
3. Примеси не конденсирующихся газов.
1% воздуха снижает теплоотдачу на 60%, 2% - на 70%. У пленки концентрация
воздуха максимальна, т.к. пар конденсируется.
4. Влияние скорости пара относительно пленки.
 - теплоотдача возрастает, т.к. пленка становится тоньше.
 - теплоотдача ухудшается, т.к. пленка утолщается. При дальнейшем
увеличении скорости частицы конденсата уносятся вверх и теплоотдача снова
может возрастать.
5. Компоновка поверхности.
а) теплоотдача на горизонтальных трубах выше, т.к. пленка
83
тоньше. Конденсат обычно стекает каплями или струйками.
б) на вертикальных трубах рекомендуется устанавливать
конденсатоотводные колпачки в виде “зонтиков” с
шагом  0,1м
в) пар лучше подавать на поверхность конденсации в виде
струй, что способствует разрушению пленок конденсата.
13.4. Теплоотдача при пузырьковом и пленочном кипении жидкости.
Кипение - процесс образования пара во всем объеме жидкости.
Для возникновения кипения всегда необходим некоторый перегрев
жидкости по отношению к температуре насыщения, т.е.
tж  tн
Обычно процесс кипячения начинается почти сразу после достижения
жидкостью температуры насыщения. При этом кипение носит спокойный
характер, что объясняется наличием в жидкости зародышей парообразования,
каковыми являются твердые микрочастицы и небольшие газовые пузырьки,
выделяющиеся при нагревании.
Градиент температуры у стенки весьма велик, хотя температура жидкости
 на 0,4К превышает температуру насыщения.
В особо чистых жидкостях при медленном их нагреве удается значительно
перегревать жидкость по отношению к температуре насыщения. Кипение при этом
носит взрывной характер в начале процесса и до тех пор, пока температура
жидкости не снизится до температуры насыщения за счет отвода тепла с паром.
При кипении жидкости на поверхности нагрева в зависимости от величины
температурного напора могут существовать несколько режимов кипения.
t = tст - tн
1. При t  5К образующиеся пузырьки пара после отрыва от поверхности
конденсируются. Теплоотдача определяется свободной конвекцией.
2. При увеличении температурного напора пузырьки пара уже достигают
свободной поверхности жидкости. При отрыве пузырьков значительно
увеличивается перемешивание в пограничном слое, что резко повышает
интенсивность теплоотдачи. Кроме того, увеличивается количество самих
пузырьков. Т.о. растет их тепловой поток, и коэффициент теплоотдачи.
Такой режим кипения называется пузырьковым.
3. При дальнейшем увеличении теплового напора отдельные пузырьки пара
на поверхности сливаются в сплошной паровой слой. Образуются паровые
полости.
Для пара
  0,02Вт/мК
Для жидкости вода  0,68Вт/мК
Теплопроводность паровых полостей сравнительно невелика, конвекция в
них незначительна, поэтому и тепловой поток и коэффициент теплоотдачи
падают. Режим называется переходным.
84
4. Пленка пара обволакивает всю стенку. Тепло от стенки к жидкости
передается за счет теплопроводности парового слоя и конвекции в нем.
Коэффициент теплоотдачи практически не изменяется.
q = (tст - tн)
Плотность теплового потока можно повысить только путем увеличения
температуры стенки. Режим называется пленочным. Однако существует опасность
пережога стенки.
Для воды
qкр1 = 1,2106 Вт/м2 ; qкр2 = 2104 Вт/м2
tкр1  30К ;
tкр2 = 150К
3
2
кр1 = 5810 Вт/м К
В условиях фиксированного потока тепла переходы от пузырькового
режима к пленочному и обратно носят кризисный характер. Переходный режим
кипения стационарно существовать не может в таких условиях.
Если тепловой поток по каким-либо причинам превысит qкр1, то количество
отводимого тепла кипящей жидкостью резко уменьшится. Это вызовет быстрый
разогрев поверхности до такой температуры, чтобы разность tст - tн обеспечивала
требуемый тепловой поток q >qкр1.
Произойдет “перескок” с кривой пузырькового кипения на линию
пленочного кипения. При этом резко повысится температура стенки.
Обратный переход к пузырьковому режиму возможен тоже только
“перескоком”. Это произойдет тогда, когда паровая пленка разрушится в какойлибо области поверхности и жидкость достигнет поверхности. В этой области
установится пузырьковый режим кипения, который повысит  и приведет к
переходу к пузырьковому режиму кипения на всей поверхности.
Вообще, применение режима кипения в зависимости от температурного
напора при кипении - яркое проявление второго закона диалектики.
1.Пузырьковый режим кипения воды.
 = 4,45 p0,15 q0,7
при 0,02 ≤ p ≤ 8 МПа
2,33 0,5
 = 146,1 t p ,
где t = tст - tн
2. Пленочный режим кипения воды.
Если использовать физическую модель, аналогичную принятой в теории
пленочной конденсации пара, то для вертикальной стенки получим:
 = 0,943 (gжп3r*/пh(tст - tн)) - при ж >>п
- при ламинарном движении
Для горизонтальных труб
 = 0,728 (gжп3r*/пd(tст - tн)) - где r*= r+0,5Ср(tст-tн)
- при ламинарном движении
Для вертикальных труб
 = 0,25 (gж Срп п2/п) при турбулентном движении.
Срп - для пара.
Пузырьковый режим кипения часто используется в технике для отвода тепла
от тепнапряженных деталей двигателей (камеры сгорания ЖРД), поршневых
двигателей рекордных автомобилей и т.п.
85
14. ТЕПЛООБМЕН ИЗЛУЧЕНИЕМ
Носителями лучистой энергии являются электромагнитные волны ,
т.е.перенос энергии вне среды .
0.40.8мкм – световые волны, видимое излучение
0,4 – ультрафиолетовые волны, ультрафиолетовое излучение
0,8800мкм – тепловые (инфракрасные волны).
Резкой границы по длинам волн не существует
Природа тепловых и световых лучей одна и та же .Законы геометрической
оптики , установленные для световых лучей, справедливы и для тепловых .
Тепловое излучение свойственно всем телам. Каждое из них излучает
энергию в окружающее пространство.
Часть лучистой энергии, поглощенная телом превращается в тепловую.
Отраженная и прошедшая части лучистой энергии распределяются между
окружающими телами.
Каждое тело непрерывно излучает и поглощает лучистую энергию.
Твердые тела излучают и поглощают энергию поверхности, газы – объемом.
Различные тела пропускают излучения различных частот по-разному
QR + QД + QА =Q0 – падающее излучение
Q A QR Q Д


1
Q0 Q0 Q0
А+Д+R=1

QA – поглощенная энергия; Q
 0
QR – отраженная энергия; 
тело
- количество энергии, падающее на

QД – прошедшая часть энергия.
A – поглощающая способность;
R – отражающая способность;
Д – пропускная способность тела (прозрачность).
1) А=1; R=0; Д=0 – абсолютно черное тело. Отверстие обладает его
свойствами
2) А=0; R=1; Д=0 – абсолютно белое тело, если отражение диффузное.
86
3) А=0; R=1; Д=0 – Зеркальное тело, если отражение по законам
геометрической
оптики
4) А=0; R=0; Д=1 – абсолютно прозрачное тело (диатермичное)
Наиболее диатермичные одноатомные газы.
Всех этих тел в природе нет.
Практически считают A + R = 1
Если тела прозрачные для видимых лучей (кварц), то это еще не значит, что
они прозрачны для тепловых.
Для поглощения и отражения значение имеет не цвет, а состояние
поверхности.
Плотность потока излучения.
Плотность потока излучения – лучистый поток, излучаемый с единицы
поверхности по всем направлениям полусферического пространства.
E
dQ
dF
; E  
Вт
м2
Е – для всех длин волн от =0 до 
Спектральная плотность измерения.
E 
dE
- для длин волн от  до 
d
E   Вт3
Е - монохроматическое излучение;
м
Превращение части внутренней энергии тела в энергию электромагнитных
волн – эмиссия.
Поглощение электромагнитных волн телом – адсорбция.
14.1. Законы теплового излучения. Закон ПЛАНКА
Устанавливает закон распределения энергии излучения по длинам волн для
абсолютно черного тела E 0 
где С1=3,74*10-6 Вт*м2
С2=1,44*10-2 м*К
если Ev 
C15
C2
e   1
dE
c
, то v 
dv

87
2hv 3
E0 v 
2
C (e
hv
kT
 1)
С увеличением температуры максимум излучение смещается в сторону
более коротких волн.
14.2. Закон ВИНА.
Т*max=2.9 [мм*К] - устанавливает соотношение между температурой и
длинной волны максимума излучения.
14.3. Закон Стефана-Больцмана
Устанавливает зависимость плотности потока излучения от температуры
4

 T 
E0   E 0  d  C 0 
 - для абсолютно черного тела
 100 
0
Вт
C 0  5.7 2
м  к2
Для других тел при этой же температуре
 T 
E  C *

 100 
4
Отношение E 
C
- степень черноты тела.
C0
Всегда Е < 1
14.4. Закон Кирхгоффа.
88
При термодинамическом равновесии отношение излучающей способности к
поглощающей не зависит от природы тела и равно энергии излучения абсолютно
черного тела при той же температуре
E
 T 
 E0  C 0 

A
 100 
4
отсюда следует, что поглощающая способность тела численно равна степени
его черноты А=Е
Спектры излучения реальных тел лежат не выше спектра излучения
абсолютно черного тела.
Если для любой длинны волны
E
 E , то тело называют серым.
E 0
14.5. Закон Ламберта.
Количество энергии, излучаемой элементом поверхности, пропорционально
количеству энергии, излучаемой по нормали, умноженному на величину
пространственного угла и направляющий косинус.
 2 Q   E n d  Cos  dF 1
Можно доказать, что E n 
E E
 E0
 
1
T 
Тогда E n  E0 C0 


 100 
4
т.е. плотность излучения по нормали в II раза
меньше полной плотности излучения тела
Теплообмен в замкнутой системе
4
4
 T   T  
q   n C 0  1    2  
 100   100  
1
n 
- приведенная степень черноты системы тел.
1
1

1
1  2
 T1  4  T2  4 
Q12  F1 n C 0 
 
 ,
 100   100  
где n 
1
, F1 – площадь меньшей поверхности

1 F1  1


 1
1 F2  E 2

14.6. Экранирование
Применяется для защиты от излучения
 T1  4  Tэ  4 
 
 
Если материал экрана и стенок одинаков, то Qiэ   n C 0 
100

  100  

89
 Tэ  4  T2  4 
Qэ 2   n C 0 
 
 
 100   100  
T14  T24
q
T 
; q1э  q э 2  12
2
2
4
э
Если взять 2 экрана, то поток уменьшится в 3 раза, для n экранов – в n+1
раз.
Общее выражение для теплового потока.
qэ

q12
1
2  Eэ E
1 n
2  E Eэ
Если E=0.8; Eэ=0,1; n=1, то
qэ
 14 !
q12
Для экранирования широко применяется алюминиевая фольга (альфоль).
14.7. Тепловое излучение газов
Газы как, и всякие тела, обладают способностью испускать и поглощать
лучистую энергию, но эта способность для различных газов неодинакова.
Одно- и двухатомные газы для тепловых лучей практически прозрачны –
(диатермичны).
Многоатомные газы обладают значительной способностью излучать и
поглощать лучистую энергию. Для теплотехники особо важное значение имеет
тепловое излучение углекислого газа и водяного пара – основных продуктов
сгорания топлива.
14.8. Особенности теплового излучения газов.
1. Газы излучают и поглощают энергию лишь в определенных интервалах
длин волн (полосах), расположенных в различных частях спектра. Для
лучей других длин волн, вне этих полос, газы прозрачны и их энергия
излучения равна нулю.
2. В газах излучение и поглощение всегда протекает в объеме
Результирующей перенос энергии определяется совместимым влиянием
обоих эффектов: поглощения и собственного испускания фотонов газовым
объемом.
90
15. ТЕПЛОПЕРЕДАЧА
Теплопередача – передача теплоты от одной подвижной среды (жидкости или
газа) к другой через разделяющую их твердую стенку (любой формы).
В общем случае количественной характеристикой процесса переноса тепла
является коэффициент теплопередачи, определяющий количество тепла,
переданного от одной жидкости к другой через единицу поверхности при разности
температур между жидкостями в один градус.
Q  kF (t Ж1  t Ж 2 )
Разность tЖ1 – tЖ2 называется температурным напором.
Сложный теплообмен.
Сочетание различных видов теплообмена может весьма разнообразным, их
весовой вклад в общем процессе теплообмена – различным.
При сложном теплообмене пользуются суммарным коэффициентом
теплоотдачи.
q  (    )(t ж  t с )   0 (t ж  t с ) если …….
а)
4
 Т Ж   Т С  4 
С 0 
 
 
 100   100  
где   
- лучистая составляющая коэффициента
t Ж tС
теплоотдачи
б)
 T Ж  4  Т С  4 
q  ( E K  E )C 0 
 
  , если главный лучистый теплообмен
 100   100  
где E K 
 t Ж  t С 
 Т Ж  4  Т С  4 
С 0 
 
 
 100   100  
- конвективная составляющая приведенной
степени черноты системы
Теплопередача включает в себе теплоотдачу от более горячей жидкости к
стенке, теплопроводность в стенке, теплоотдачу от стенки к более холодной
подвижной среде.
Заданы: ; tЖ1; tЖ2; 1; 2.
При стационарном режиме тепловой поток, проходящий через плоскую стенку
составит
t t
q 1 2


91
Этот тепловой поток при передаче от горячей жидкости к стенке составляет
q  1 t Ж1  t1 
Этот же тепловой поток при передаче
Граничные


условия III рода 
от стенки к холодной жидкости составит
q   2 t 2  t Ж 2 
q

t Ж1  t1  
1

q

t1  t 2 


q

t 2  t Ж 2  
2

 1 
1 
,
t Ж1  t Ж 2  q  
 1   2 
q 
K
K  

1
 1
tЖ 1  t Ж 2
1

1


 1

 2
1
- коэффициент теплопередачи

1



 2
ВТ
- такая же, как и у коэффициента теплопередачи
м K
Тогда
2
q  K (t Ж 1  t Ж 2 )
Q  K (t Ж 1  t Ж 2 ) F
Коэффициент теплопередачи численно равен количеству теплоты, которое
передается через единицу поверхности разделительной стенки при разности
температур теплоносителей 1К.
1
1 
1

 
- термическое сопротивление теплопередачи
K 1   2
1 1
;
- термическое сопротивление теплоотдачи
1  2
R
Очевидно, что для многослойной стенки термическое сопротивление равно
сумме термических сопротивлений слоев.
R
n

1
1
1
  i 
K 1 i1 i  2
92
Плотность теплового потока через многослойную стенку составит:
q 
1
 1
tЖ 1  tЖ 2
n
 i
1
 

 2
i1  i
Уравнение подобно уравнению теплопроводности для многослойной плоской
стенки
Тепловой поток составит
Q  qF  kF (t Ж 1  t Ж 2 )  kF t
Температуры поверхностей стенки составят
t1  t Ж 1  q
1
1
t 2  t Ж1  q
 1  

1
 q 1  t Ж 1  q  1 
1
1
  1 1 
t3  t Ж1  q
 1 


 
1
 q 1  q 2  t Ж1  q  1  2 
1
1
2
  1 1  2 
n
 1
 
t i 1  t Ж1  q   i  - в общем виде
  1 i 1 i 
Это уравнение пригодно для расчета граничных температур любых слоев.
15.1. Теплопередача через цилиндрическую стенку.
Заданы: ; tЖ1; tЖ2; 1 и 2.
Если l  , то потерями с торцов трубы
можно пренебречь
При установившемся режиме через стенку будет
проходить и отдаваться жидкости одно и тоже
количество теплоты

q   2 r t  t 
1
1 Ж1
1
 e

2 (t1  t 2 )
q e 
r
1

 ln 2


r1

qe   2 * 2 r2 (t 2  t Ж 2 )

qe
t Ж1  t1 
2 r1 1


qe
r
 ln 2
t1  t 2 
2 
r1


qe
t 2  t Ж 2 
2 r2 2

отсюда
93
qe 
2 П (t Ж 1  t Ж 2 )
1
1
r2
1

ln

 1 r1

r1
 2 r2
Если обозначить
Ke
2

1
 1 r1
1

ln

r2
1

r1
 2 r2
- линейный коэффициент теплопередачи
q e  k e (t Ж 1  t Ж 2 )
Q  k el  t
Для тонких труб можно воспользоваться выражением (если r2/r1 < 1.8)
Q  k 2 rx l  t , где
rx = r2 если 1>>2
rx = r1 если 1<<2
rx = r cp если 1
В случае теплопередачи через многослойную цилиндрическую стенку
выражение для плотности теплового потока приобретает
вид qе 
2 П (t ж1  t ж 2 )
r j 1
1
n
1
1
  j 1 ln

1 r1
j
r j  2 r2
Граничные условия 1 рода можно рассматривать как частный случай
граничных
условий 3 рода, когда  1  
и  2  ,а
соответственно t ж1 t 1 и t ж 2 t 2
15.2. Критический диаметр тепловой изоляции.
Тепловая изоляция – покрытие горячей поверхности, которое способствует
снижению потерь теплоты в окружающую среду.
Для тепловой изоляции используют материалы с низким коэффициентом
теплопроводности (опилки, асбест, шлаковая вата и др.).
Общее термическое сопротивление двухслойной цилиндрической стенки
определяется по формуле (труба в изоляции):
Rцил 
Если d3
d
d
1
1
1
1
1


ln 2 
ln 3 
K цил 1 d1 21 d1 2 2 d 2  2 d 3
d
1
ln 3
2 2 d 2
1
2 d 3
dR4
1
1


 0 - при этом Rцик
dd 3 2 2 d 3  2 d 3 2
d кр  d из 
2 2 2из

2
2
d кр 
min
2из
2
94
Выводы: 1) dкр не зависит от d1, d2, 1, 1
2) dкр соответствует минимуму теплового сопротивления,
максимуму теплового потока
Для того чтобы изоляция вызывала уменьшение теплопотерь
цилиндрической стенки по сравнению с оголенным трубопроводом, необходимо
чтобы выполнялось условие
из 
 2d3
2
15.3. Пути интенсификации теплопередачи.
Из уравнения теплопередачи Q=kFt следует, что при фиксированных
размерах стены и температурном напоре величиной, определяющей
теплопередачу, является коэффициент теплопередачи К.
Для плоской, тонкостенной цилиндрической стенок
K
Если
1
1 
1
 
1   2
1
1

1

1

и

, то можно полагать, что K `

1
1


2

1

1 1
1  2
2
1) Если 2  , то K` 1
2) Всегда K`<
3) Если 2 >> 1, то K`  1
Следовательно, увеличение K` возможно только при увеличении меньшего
из двух коэффициентов теплоотдачи.
15.4. Оребрение стенок
Q  kF t 
F t
t
t


1 
1
1

1
1
 



 1   2  1 F F  2 F  1 F  2 F
Если увеличить поверхность стенки с меньшим коэффициентом
теплоотдачи таким образом , что оба члена в знаменателе будут равными , то
коэффициент теплопередачи как бы увеличится .
Поэтому широко применяется оребрение поверхностей .
Q
F1 t
, где F2>F1
F1
1 
 
 1   2 F2
Помимо оребрения применяется обдув поверхностей вдоль плоскостей ребер.
95
15.5. Сложный теплообмен
Сочетание различных видов теплообмена может быть весьма
разрушительным, а их весовой вклад в общем процессе теплообмена – различным.
Обычно учитывают тот вид теплообмена, который в данном явлении или
процессе является превалирующим, а влияние остальных видов теплообмена
учитывают соответствующими корректировками.
Процесс переноса теплоты между потоком излучающего газа и стенкой
является результатом действия как конвективного теплообмена, так и теплового
излучения. Такой теплообмен называют сложным.
Количество переданного тепла при этом определяют по формуле
q   0 t Ж  t Ж 
где 0 = К + Л – суммарный коэффициент теплоотдачи
Л – лучистая составляющая коэффициента теплоотдачи.
 Т Ж  4  Т С  4 
 
 

 100   100  
   ЕС0
t Ж  tС
T
 100 
  0,04 ЕС0  CP 
3
Если в теплообмене преобладает тепловое излучение, то
 T Ж  4  Tc  4 
q  ( E k  E )C 0 
 
 
 100   100  
Участие в процессе конвективного теплообмена здесь учитывается
увеличением приведенной степени черноты системы путем введения ЕК
EK 
 K t Ж  t С 
4
4
 Т   Т  
С 0  Ж    С  
 100   100  

K
T 
C 0 0.04 C 
 100 
3
96
16. ТЕПЛООБМЕННЫЕ АППАРАТЫ.
16.1. Типы теплообменных аппаратов.
Теплообменный аппарат - устройство для передачи тепла от одного
теплоносителя к другому.
Теплообмен между теплоносителя широко используется в технике.
Теплообменные аппараты многочисленны и весьма разнообразны по назначению,
оформлению. По принципу действия они разделяются на :
1. Рекуперативные
2. Регенеративные  поверхностные
3. Смесительные
1. Рекуперативные ТА - устройства, в которых две жидкости с различными
температурами разделены твердой стенкой.
Теплообмен происходит за счет теплоотдачи и теплопроводности стенки.
Если одна из жидкостей  измеряющий газ (например - топки паровых котлов), то
имеет место также тепловое излучение.
2. Регенеративная ТА - устройства, в которых одна и та же поверхность
омывается то горячим, то холодным теплоносителям. Тепло воспринимается
стенками
аппарата
и
аккумулируется
в
них.
Пример:
кауперы,
воздухоподогреватели котлоагрегатов.
97
3. Смесительные ТА - процесс теплопередачи происходит путем
непосредственного контакта и смешения горячей и холодной жидкостей.
Пример : 1) градарил - вода охлаждается атмосферным воздухом. Вода при
этом частично испаряется, т.е. имеет место массообмен.
2) ртутно-водяные теплообменники в бинарных установках.
3) скрубберы (химическая промышленность)
Для увеличения поверхности теплообмена в смесительных теплообменниках
применяются различной формы насадки.
16.2. Тепловой расчет теплообменных аппаратов.
Тепловой расчет ТА может быть :
1. Проектный (конструкторский)
Известны : t1 ; t1 ; t2 ; t2 ; G2 .
Определить : F - поверхность теплообмена.
2. Поверочный
Известны : F и др. параметры
Определить : t1 ; t2
Основными уравнениями при расчете являются уравнение теплового
баланса и уравнение теплопередачи.
1. Q1 = Q2 + Q, где Q - потери тепла в окружающую среду
Q = Q1 = Q2 - тепловая мощность теплообменника
Q = пm1  i1 = m2 i2
Если пренебречь потерями, то
Q = G1 Cp1 (t1 - t2) = G2 Cp2 (t2 - t1), где
G1,G2 - массовые расходы теплоносителей;
Cp1,Cp2 - средние теплоемкости в соответствующих интервалах
температур.
W1 = G1 Cp1
W2 = G2 Cp2
- водяные эквиваленты.


W1/W2 = (t2 - t2 )/(t1- t1);
[W] = Вт/К
Водяной эквивалент численно равен теплоемкости секундной массы
теплоносителя.
Отношение водяных эквивалентов обратно пропорционально отношению
изменений температур теплоносителей.
2. Уравнение теплопередачи.
Q = KF(t1 - t2) = KFt
Но температурный напор может изменяться по длине поверхности
теплообмена.
Характер изменения температуры жидкостей вдоль поверхности
теплообмена зависит от схемы их движения и соотношения значений водяных
эквивалентов.
98
Если направления движения теплоносителей совпадают, то такая схема
называется прямоточной.


Если направление движения горячего теплоносителя противоположно
направлению движения холодного, то такая схема называется противоточной.


Иногда
организовывают
также
перекрестные
схемы
движения
теплоносителей.

16.3. Средний температурный напор.
tср = (t1+t1)/2 - (t2-t2)/2
Это уравнение может применяться при небольших изменениях температуры
теплоносителей и температурного напора.
dQ = KdFt
т.к. t = t1 - t2
dQ = -G1Cp1dt1 = G2Cp2dt2
dt1 = - dQ/G1Сp1; dt2 = -dQ/G2Cp2
d(t) = dt1 - dt2 = - dQ/G1Cp1 - dQ/G2Cp2
dQ = -d(t)/(1/G1Cp1+1/G2Cp2)
1/G1Cp1+1/G2Cp = n
dQ =-d(t)/n
-d(t)/n= KdFt;
-d(t)/t = KndF
t2
F
t1 d(t)/t = 0 KndF; Ln(t1/t2) = KnF
n = (Ln(t1/t2))/KF (1)
Интегрируем dQ = -d(t)/n; Q = -t1t2(d(t)/n)
Получим:
Q = (t1 - t2)/n.
(2)
Тогда из (1) и (2) получим
Q = (t1 - t2)/(Ln(t1/t2))KF
Q = tcpKF
tcp = (tб-tм)/(Ln(tб/tм))
Уравнение (при tб = tм) для среднелогарифмического температурного
напора является вырожденным. В этом случае следует применять уравнение для
среднеарифметического температурного напора.
Среднеарифметическое значение температурного напора всегда больше
среднелогарифмического.
При t/t > 0,6 отличие меньше 3%.
Температурный напор при прямотоке изменяется сильнее, чем при
противопотоке. Среднее значение температурного напора при противопотоке
больше, чем при прямотоке. Поэтому при портивопотоке теплообменники
получаются компактнее.
Если температура одной из рабочих жидкостей постоянна, то среднее
значение температурного напора не зависит от схемы движения. Именно это
происходит при кипении жидкости или конденсации пара.
99
Коэффициент теплопередачи изменяется вдоль поверхности теплообмена. В
первую очередь это определяется тем, что изменяются коэффициенты
теплоотдачи, входящие в общую формулу.
Коэффициенты теплоотдачи обычно определяют для средних температур
рабочих жидкостей.
Иногда определяют коэффициенты теплопередачи в начале и в конце
поверхности теплообмена (К и К) и затем находят средний коэффициент
теплопередачи
К=(К+ К) /2
16.4. Расчет конечной температуры рабочих жидкостей.
Цель проверочного расчета - определение конечных температур
теплоносителей.
Ранее было определено, что температурный напор изменяется по
экспоненциальному закону (см. формулу 1 на рис. 34)
n = Ln (t1/t2)/ kF , где n =1/W1 + 1/W2
Тогда
n = Ln (t/t)/kF
nkF = Ln (t/t) ; Ln (t/t) = - nkF
t = t  e-nkF
В конце поверхности нагрева
t = t1 - t2 ;
Тогда
t1 - t2 / t1 - t2 = e-nkF
1 - (t1 - t2 / t1 - t2) = 1 - e-nkF
(t1 - t2) - (t1 - t2) = (t1 - t2)(1 - e-nkF)
(t1 - t1) + (t2 - t2) = (t1 - t2)(1 - e-nkF)
(t1 - t1) + (t2 - t2)W1/W2 = (t1 - t2)(1 - e-nkF)
t1 - t1 = (t1 - t2) [(1 - e-nkF)/1 + (W1/W2)]
t1 - t1 = (t1 - t2) 
 = (W1/W2 ; kF/W1)
t2 - t2 = (t1 - t2)W1 W2 
Значение функции  даются в литературе (Михеев М.А.)
Для противоточных теплообменных аппаратов рассуждая аналогично
получим :
t1 - t1 = (t1 - t2)Z
t2 - t2 = (t1 - t2)W1/W2Z
Z = (W1/W2 ; kF/W1)
Функция Z и  позволяют вычислить промежуточные значения температуры
рабочих жидкостей.
Прямоток может быть применен, если :
1. W1/W2 < 0,05 или W1/W2 > 10
100
Изменение температуры одной жидкости незначительно по сравнению с
изменением температуры другой жидкости.
2. Если kF/W2 или kF/W1 малая величина.
Тогда средний температурный напор значительно превышает изменение
температуры жидкости.
16.5. Гидравлический расчет теплообменных аппаратов.
Целью
гидравлического
(гидромеханического)
расчета
является
определение величины потери давления теплоносителя при прохождении его
через аппарат.
При движении жидкости всегда имеют место сопротивления,
препятствующие движению. На преодоление этих сопротивлений необходимо
затрачивать механическую энергию. Энергия эта пропорциональна перепаду
давления p.
Гидравлические сопротивления разделяют на сопротивление трения
(сопротивление по длине) и местные сопротивления.
1. Сопротивление трения обусловлено вязкостью жидкости и проявляется
при безотрывном движении жидкости вдоль твердой стенки. При равномерном
движении сила трения равна силе давления.
В общем случае потери на трение определяются по формуле
pтр = ( l/d + 0) w2/2
где l - длина,
d - гидравлический диаметр канала.
0 - поправка на начальный участок.
Практически применяется формула Дарси
pтр = l/d  w2/2 , где
 - коэффициент сопротивления трения.
2. Местные сопротивления обусловлены вихреобразованием в местных
сопротивлениях (выход, вход, сужение, расширение, поворот и т.п.). Их величина
определяется по формуле Вейсбаха.
pм = (w2/2), где
 - коэффициент местного сопротивления.
 - его значения определяются по справочной литературе.
3. Дополнительные сопротивления возникают вследствии применения
плотности газа при изменении его температуры.
py = 2(2 w22/2 - 2 w22/2) = 2w22 - 1w21
Если w2 > w1 , то газ ускоряется и py - положительная величина.
4. Сопротивление “самотяги” возникает вследствии изменения плотности
жидкости с температурой.
pc = g( - ) h
где h - высота вертикального канала (газохода),
 - плотность холодной жидкости.
Если газы движутся вниз, то сопротивление самотяги увеличивает общее
сопротивление канала, если вверх - то уменьшает.
101
Полное сопротивление определяется по формуле
р = ртр + рм + рy + рс
Расчетные формулы для .
 = 64/Re - формула Пуазейля
Re < 2300
-0,25
 = 0,3164 Re
- формула Блазиуса
3103 < Re < 105
 = 0,0032 + 0,221/Re0,237 - формула Никурадзе 105 < Re < 108
 = 1/(1,82 LgRe - 1,64)2 - единая формула.
16.6. Расчет мощности на перемещение теплоносителей.
Nгидр. = р  F  W = p  (G/) - мощность на перемещение теплоносителя.
Nнас. = Nгидр./ = pG/ - мощность насоса для перемещения теплоносителя.
Для реализации регенеративных циклов необходимо теплообменные
аппараты. Если мощность, потребная на перемещение теплоносителей превышает
сэкономленную мощность (благодаря применению регенерации тепла), то
теплообменный аппарат устанавливать нецелесообразно.
102
17. ТОПЛИВО И ПРОЦЕССЫ ГОРЕНИЯ
В данной лекции рассматриваются следующие вопросы:
1. Химический состав и теплота сгорания топлива. Понятие об условном топливе.
2. Краткая характеристика естественных и искусственных топлив.
3. Расчеты процессов горения топлива.
4. Кинетика гомогенных реакций горения.
5. Самовоспламенение и зажигание горючей смеси.
6. Массо- и теплообмен в пламени. Горение газообразных топлив. Детонация.
Топливо – горючее вещество, сжигаемое для получения тепла.
По своему агрегатному состоянию топлива делятся на твердые, жидкие и
газообразные. По происхождению топлива делятся на естественные и
искусственные. И те, и другие могут быть в любом агрегатном состоянии.
17.1. Химический состав и теплота сгорания топлива. Понятия об
условном топливе.
Свойства топлива как горючего материала определяются его горючей массой,
которую характеризуют массовым содержанием следующих элементов. Она
приводится в таблицах
C Г  Н Г  О Г  N Г  S Г  100%
S   летучая сера, входящая в состав органических и колчеданных соединений.
Сухая масса топлива включает в себя также золу.
C c  H c  O c  N c  S c  Ac  100% ,
где Ас – зола.
Рабочая масса топлива содержит также влагу
p
p
C p  H p  O p  N p  Sp  
A
W


  100% ,
Б баласт
p
где W – влага.
Состав рабочей массы можно получить по формуле:
100  Б 

100

100  А р  W p
p
 100  Б 
р
г
H H
Э =Э
100
100

.............. 
C p  C
Состав газообразных топлив обычно задается в объемных долях.
Важнейшей энергетической характеристикой топлива является теплота сгорания.
Другими характеристиками являются: содержание золы и влаги выход летучих
веществ, свойства нелетучего остатка (кокса).
Теплота сгорания топлива – количество теплоты, выделяющееся при полном
сгорания единицы массы топлива.
Различают высшую и низшую теплоту сгорания топлива.
103
Высшая теплота сгорания учитывает теплоту конденсации водяных паров при
охлаждении продуктов сгорания до начальной температуры топлива. Низшая
теплота сгорания меньше высшей на величину теплоты парообразования влаги
топлива (WP) или образующейся при сгорании водорода, входящего в состав
топлива.
Низшая теплота сгорания определяется по формуле Д. И. Менделеева.
QHP  338C P  1025H P  108(O P  S P )  25W P ,кДж/кг.
Высшая теплота сгорания топлива определяется из выражения:
QBP  QHP  226 H P  25W p  QHP  r (9 H P  W P ) ,
кДж
- скрытая теплота парообразования при давлении паров 10
кг
кПа, характерном для большинства энергетических установок.
Условное топливо – топливо, имеющее принятую теплоту сгорания 29350 кДж/кг.
Понятие условного топлива используется для сравнительных и экономических
расчетов. Для пересчета действительного количества топлива в условное
используют коэффициент эквивалентности.
QHP
Э
29350
кДж
P
Пример: Для дров QH  10000 кг тогда эквивалент 1 кг дров составит (по
10000
 0.34кг ).
условному топливу Э 
29350
где r  25.11
17.2. Краткая характеристика естественных и искусственных топлив
Твердое топливо
МДж
кг
Используется как местное топливо. Влажность торфа до 50%.
МДж
QHP  10...17
Бурые угли.
кг
Имеют высокую зольность, относятся к низкосортным углям.
МДж
P
Каменные угли. Q H  23...27
кг
Их классифицируют по выходу летучих и характеру коксового остатка.
P
Древесина, торф. Q H  10...15
МДж
P
Антрацит – уголь с высоким содержанием углерода QH  30...35 кг
Жидкое топливо.
Нефть. В качестве топлива обычно не применяют.
Бензин, керосин, соляровое масло получают перегонкой нефти. Используются
как топлива для ДВС, ГТУ
МДж
QHP  38...43
кг
104
Мазут. Широко используется в теплоэнергетике.
МДж
QHP  40...42
кг
Газообразное топливо.
Природный газ. Содержит 90 – 98 % метана. Используется как топливо для ГТУ
на газоперекачивающих станциях.
QHP  35...37
МДж
м3
Генераторный газ. Получают газификацией твердых топлив.
QHP  5...7
Доменный газ.
Q HP  3...4
МДж
м3
МДж
м3
P
Жидкие газы (этан, пропан, бутан) QH  95
МДж
. Применяются в качестве
м3
топлива для ДВС, ГТУ.
17.3. Расчет процессов горения топлива.
Горение – химический процесс соединения топлива с окислителем,
сопровождающийся интенсивным выделением тепла и повышением
температуры продуктов сгорания.
В расчетах процессов горения важным является определение количества
окислителя, необходимого для сжигания топлива. Оно определяется на основе
стехиометрических уравнений
Н2 + ½О2 = Н2О
1кг Н2 + 8кг О2  9кг Н2О 1:8
С + О2 = СО2
12кг С + 32кг О2  44кг СО2 1:2,67
S + O2 =SO2
32кг S + 32кг О2  64кг SO2 1:1
Количество воздуха, необходимое для сжигания 1кг топлива определяется из
соотношения
8
1
кг
L0  ( C P  8H P  SP  O P ) 
,
3
100 0.232 кг
где 0.232 – весовая доля кислорода в воздухе.
Объемный расход воздуха при нормальных условиях составит (при p =
1.293 кг/м3)
м3
0
p
P
P
P
V  0.033(2.67C  8H  S   O ),
кг
В реальных процессах горения воздух подают в несколько больших
количествах. Vg > V0 – обычно имеет место такое неравенство.
V
Отношение   V 0
называют коэффициентом избытка воздуха.
Коэффициент избытка воздуха – отношение действительного количества
воздуха, подаваемого камеру сгорания, к теоретически необходимому количеству
105
воздуха. Обычно в хороших топочных устройствах  = 1.05 – 1.2, в ДВС – до 1.8, в
ГТУ – 3 - 5.
Состав и объем продуктов сгорания
При организации процессов горения стремятся обеспечить по возможности
полное сгорание топлива.
Основные компоненты продуктов сгорания:
СО2, SO2 – RO2
H2O
N2
O2 – “избыточный” кислород воздуха
CO
H2
NO



 их доля обычно невелика

прочие 
VCO  VSO  0.0168(C P  0.375S opP  k )
2
2
VH O  0.111H P  0.0124W P
2
VГ  VCO  VSO  0.79 BV 0  0.21( B  1)V 0
2
2
Для топлив в справочной и нормативной литературе приводят значение
V 0 ,VRO иVH O .
Эти формулы позволяют рассчитать, теплоемкость, энтальпию продуктов
сгорания.
2
2
Энтальпия продуктов сгорания
Энтальпию принято относить к 1кг топлива, из которого получились
продукты сгорания.
Дж
[J  ] 
I   V  C   t .
кг
Объем продуктов сгорания на единицу количества топлива увеличивается с
увеличением коэффициента избытка воздуха.
I   I O  ( B  1) I BO
O
O
Для всех топлив величины I  (иI B ) даются в справочниках. Для расчетов
используются I – t диаграммы.
Адибатная температура – температура, которую имели бы продукты
сгорания при отсутствии теплопотерь в окружающую среду в процессе сгорания.
Адиабатная температура максимальна для стехиометрической смеси (В=1).
С увеличением коэффициента избытка воздуха на нагрев “избыточного” воздуха
затрачивается лишняя теплота, поэтому температура продуктов сгорания
уменьшается.
Теоретические температуры горения.
Н2 – 2370 0С
СО – 2230 0С
106
СН4 – 2030 0С
Доменный – 1410 0С
При нагреве воздуха, подаваемого в топку, или обогащении его кислородом
температура горения увеличивается.
Кинетика гомогенных реакций горения газа.
Гомогенной называется реакция, протекающая между компонентами,
находящимися в одной фазе.
W1  K1  C Aa  CBb    C Nn - скорость прямой реакции
а, b, …, n – стехиометрические коэффициенты;
К – константа скорости реакции.

E
RT
k  k0е
- уравнение Аррениуса
Е – энергия активации; [E]=Дж/моль
Скорость гомогенной реакции – количество данного компонента,
прореагировавшего в единице объема в единицу времени.
Установлено, что вероятность реакции по схеме 2Н2 + О2 = 2Н2О ничтожно
мала. Теории цепных реакций (Н. Н. Семенов) допускают существование
свободных атомов водорода и кислорода.
НО + Н2 = Н2О + Н
Н + О2 = НО + О
О + Н2 = ОН + Н
По мере накопления молекул воды количество свободных радикалов и
атомов уменьшается и реакция замедляется.
В горении СО, по-видимому, большое значение имеет наличие атомов
водорода. Сухая СО горит очень медленно.
Самовоспламенение и зажигание горючей смеси.
Самовоспламенение – инициирование горения во всем объеме смеси.
Самовоспламенение смеси происходит лишь в том случае, когда тепловыделение в
реакции превышает теплопотери. Скорость реакции экспоненциально растет с
температурой, теплопотери вследствие теплоотдачи зависят от температуры
линейно.
Температуры самовоспламенения в смеси с воздухом
Н2 – 580-590 0С
~585 0С
СО – 644-638 0С
~651 0С
СН4 – 650-750 0С
~700 0С
С2Н2 – 406-440 0С
~423 0С
Обычно горение инициируется с помощью зажигания вспомогательными
устройствами (факел, раскаленный предмет, электрическая искра). Возникает
фронт пламени, распространяющейся в объеме смеси.
Тв – температура самовоспламенения.
107
17.4. Массо- и теплообмен в пламени.
Горение газообразных топлив. Детонация.
Принудительное воспламенение горючей смеси возможно лишь в
определенных пределах по концентрации. Горючая смесь может подаваться в зону
горения в готовом виде. В этом случае скорость распространения фронта пламени
определяется только кинетикой химических реакций. Такое горение называется
кинетическим, а пламя – нормальным.
Если топливо и окислитель подаются в зону горения раздельно, то в этом
случае имеет место диффузионное горение.
Горение жидких топлив протекает в парогазовой фазе. Интенсивность
испарения топлива определяется тонкостью его распыливания. Для повышения
тонкости распыливания необходимо снимать вязкость топлива.
Мазут перед подачей в форсунки подогревают до 350 – 400 К.
Твердое топливо подается в зону горения в виде твердых частиц. В процессе
прогрева испаряется влага и происходит выделение летучих веществ. Эти летучие
вещества воспламеняются первыми. Они прогревают твердый остаток, который
сгорает в последнюю очередь. Образующаяся при этом зола препятствует
горению. Плавление золы приводит к ошлаковыванию твердых частиц и еще
более ухудшает доступ кислорода к топливу.
Нормальное пламя.
Нормальное пламя – пламя, распространяющееся путем передачи тепла
теплопроводностью из зоны горения, в свежую смесь.
Тщательно перемешанная смесь горючего и окислителя сгорают обычно в
виде пламени определяется только кинетикой реакций (а не скоростью смешения
реагентов).
Процесс горения (химического взаимодействия молекул горючего и
окислителя) протекает в зоне толщиной порядка 0.01 – 0.1 мм. зона догорания
составляет порядка 10 мм.
Чем выше температура в зоне пламени, тем выше скорость химической
реакции и, соответственно скорость распространения пламени.
Существуют концентрационные пределы распространения пламени. Водород
< 4.1 % и > 75 % в смеси с воздухом невозможно зажечь. Обычно скорости
распространения пламени лежат в пределах порядка долей м/с (0.3 – 0.5 м/с).
Наибольшие получены для водорода (13 м/с) и ацетилена (15.4 м/с).
В узких щелях толщиной менее ~1 мм пламя распространяться не может
вследствие интенсивного охлаждения (Лампа Г. Дэви).
Турбулентное пламя.
При переходе от ламинарного режима движения газа к турбулентному
турбулентные пульсации скорости потока искривляют фронт пламени,
увеличивают его поверхность. Соответственно увеличивается количество
сгорающей смеси без удлинения факела.
Вследствие турбулентного перемешивания происходит смешение свежей
смеси с продуктами сгорания в большом объеме. Чем интенсивнее
108
перемешивание, тем интенсивнее сгорание. В результате длина турбулентного
факела мало зависит от скорости истечения смеси.
Величина скорости турбулентного сгорания смеси в цилиндрах ДВС
составляет порядка 25 – 40 м/с.
Детонация
Детонация – поджигание смеси топлива ударной волной и распространение
фронта пламени с ударной волной.
Толщина фронта ударной волны порядка 0.1 мкм. Смесь сгорает значительно
быстрее, чем в нормальном пламени. Скорость распространения фронта пламени
составляет порядка 2000 м/с. В определенных условиях в детонацию способно
переходить и нормальное пламя.
Для предотвращения детонации в карбюраторных ДВС в топливо добавляют
антидетонаторы. Тетраэтил свинца Рb(С2Н5)4 – наиболее распространенный
антидетонатор. Очень токсичное вещество.
Склонность топлива к детонации оценивается октановым числом.

Гептан С 7 Н 16  О
 условные числа
Изооктан С 8 Н 18  100 

Диффузионное пламя.
Диффузионное пламя образуется при диффузионном горении, которое
осуществляется при раздельной подаче горючего и окислителя. Фронт
диффузионного пламени разделяет потоки топлива и окислителя. Положение
фронта пламени и скорость сгорания в нем (и соответственно длина факела)
определяются интенсивностью диффузии горючего и окислителя и продуктов
сгорания.
Диффузионный факел длиннее, чем факел подготовленной смеси, но в
технике часто применяют сжигание топлива при разделенной подаче его с
окислителем причины этого:
1. Безопасность с точки зрения возможности взрыва и пожара.
2. Удлинения зоны нагрева поверхности (в печах, котельных агрегатах и т. п.).
Примером диффузионного пламени может служить пламя спички, свечи.
109
Литература и методические указания:
Основаная:
1. Теплотехника / А.И.Басков, Б.В.Берг, О.К.Витт и др.; Под ред. А.П.Баскова. –
М.: Энергоатомиздат, 1991. –224 с.
2. Алабовский А.Н., Недужий И.А. Техническая термодинамика и теплопередача.
– Киев: Вища школа, 1990. –255 с.
3. Теплотехника / А.М.Архипов, С.И.Исаев, И.А.Кожинов и др.; Под ред.
В.И.Крутова. – М.: Машиностроение, 1986. –432 с.
4. Теплотехника / Алабовский А.И., Константинов С.М., Недужий И.А.: Под ред.
С.М.Константинова. Киев: Вища школа, 1986. –255с.
Вспомогательные:
1. Техническая термодинамика В.И.Крутов, С.И.Исаев, И.А.Кожинов и др.: Под
ред. В.И.Крутова. –М.:Высш.шк., 1991. –384 с.
2. Алексеев Г.И. Общая теплотехника. –М.:Высшая школа, 1980. –552с.
3. Михеев М.А., Михеева И.М. Основы теплопередачи. –М.:Энергия, 1977. –320с.
Методические указания:
Методические указания к использованию ТСО в курсе «Теплотехника» (для
студентов специальности ПТСМО) /Сост. С.А.Горожанкин. –Макеевка: МакИСИ,
1988. –43с.
110