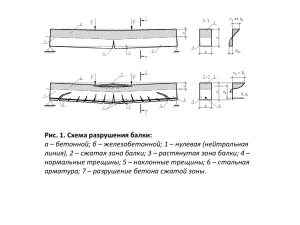
Тема 2 Что такое железобетон и для чего он нужен? Железобетон представляет собой комплексный строительный материал, состоящий из рационально соединенных для работы в конструкции бетона и стальных стержней. Преимущества железобетона: • • • • • • • • • Более высокие, по сравнению с другими материалами, прочность и долговечность; Высокая огнестойкость, радиационная стойкость; Способность сопротивляться динамическим нагрузкам; Минимальное изъятие природных ресурсов при производстве и максимальное использование отходов из других отраслей. Сочетаемость с другими материалами; Возможность переработки для строительных или иных нужд; Экономичность; Высокие эстетические и архитектурные качества, легкая формуемость; Экологическая безопасность при производстве и эксплуатации. Недостатки железобетона: • Большая плотность (собственный вес); • Высокая тепло- и звукопроводность; • Трудоемкость усиления; • Необходимость выдержки для набора прочности; • Возникновение трещин даже при небольших растягивающих напряжениях Перспективы развития железобетона: • Повышение прочности бетона до 60-200 МПа, применение легких конструктивных элементов; • Повышение прочности арматуры и использование предварительного напряжения; • Применение эффективных конструкций (например, оболочек); • Улучшение технологии изготовления железобетона; • Использование современной аппаратуры для контроля качества ЖБК. Области применения железобетона Железобетонные типовые крупноблочные и панельные здания Крупнопанельный жилой дом серии И-155, с 2001-н.в. Крупноблочный жилой дом cерии II-18, 1962- 1972, в Москве их 981 Панельное железобетонное здание серии К-7, 1958-1970, в Москве в программу сноса пятиэтажек включено 1722 здания Монтаж панельного здания серии К-7 Панельные дома КОПЭ-80 (с 1980 г.) и КОПЭ-85 (с 1985 г.), 12-25 этажа, Очаковский завод ЖБИ в составе ДСК-2, Москва (1980-2017) (Каталожный Объемный Планировочный Элемент) Панельные дома серии П-44Т (9-25 этажа), Москва и МО, (1997-2019), возведено около 800 домов Панельные дома серии П-44ТМ/25 (ТМ-25), 25 этажей, Москва и МО, ДСК-1, с 2005 г. Монтаж панельного здания серии ПИК-1, с 2016 г. Панельное здание серии ПИК-1, секции 16 и 25 этажей Железобетонные монолитные здания: • • • • • • • • Жилые здания; Административные здания; Торговые комплексы; Выставочные залы; Учебные заведения; Театры; Библиотеки; Гостиницы Промышленные здания Мосты Коммунальный мост через Енисей (г. Красноярск, 1961 г.), общая длина 2300 м, высота 23.4 м, ширина 26 м, судоходный пролет – 158 м. Инженерные сооружения Тоннели Дымовые трубы Плотины Резервуары Эстакады Высотные сооружения из железобетона Останкинская телебашня (537 м) Телебашня в Торонто (555 м) Высотные здания из железобетона «Петронас» в Куала-Лумпуре (Малайзия), 582 м, 1999г. Высотные здания из железобетона «Бурдж-Хали́фа», Дюбай, 828 м, 2010 г. Высотные сооружения из железобетона Платформа «Тролль» для добычи нефти в Норвегии высотой 472 м, платформа установлена на глубине 300 м и рассчитана на действие шторма с высотой волны 31,5 м, вес 683 600 тонн Железобетонные оболочки Защитная оболочка АЭС Куданкулам в Индии (2002 г.) Оболочка в виде правильного треугольника, перекрывающая Дворец техники (CNIT) в Париже Рис. Здание оперного театра в Сиднее, 1959-1973 Монолитный железобетон Достоинства монолитного железобетона: • • • • Возможность придать любую форму; Большая жесткость монолитных конструкций; Герметичность (для резервуаров и подземных сооружений) Экономичность по расходу металла. Недостатки монолитного железобетона: • • • Сезонность работ; Большая трудоемкость (по сравнению со сборным); Большой расход материалов на опалубку; Сборный железобетон Достоинства сборного железобетона: • • • • • Изготовление в заводских условиях позволяет существенно улучшить качество конструкций; Уменьшается трудоемкость монтажа; Снижается расход материалов на производство подмостей и опалубки; Возможность использования бетона и арматуры высоких марок; Сокращение сроков строительства. Недостатки сборного железобетона: • • • • Необходимость производства дополнительных работ (и затрат) на обеспечение герметичности (в подземных сооружениях); Меньшая жесткость конструктивного решения из-за того, что требуется омоноличивать выпуски арматуры в узлах Дополнительные расходы на транспортировку; Большая материалоёмкость стыков (закладные детали и бетон омоноличивания); Стык колонны с ригелем до омоноличивания Сборные ЖБ конструкции одноэтажного промышленного здания Сборно-монолитный железобетон Достоинства: • Сохранение всех достоинств монолитной конструкции; • Сокращение арматурных и, особенно, опалубочных работ, снижение трудоемкости, сокращение сроков строительства; • Сокращение затрат на опалубку; Недостатки: • Необходимость выполнения дополнительных мероприятий, обеспечивающих монолитность конструкции (соединение старого бетона с новым за счет выпусков, механической и химической обработки); • Ограниченность использования данного конструктивного решения в сооружении (в основном, только в покрытиях). Сборно-монолитное перекрытие Сущность работы железобетона 1. Укрепление растянутой зоны бетонной конструкции Рис. Характер работы под нагрузкой чисто бетонной и армированной бетонной балок Основная идея применения железобетона в изгибаемых конструцкциях заключается в том, чтобы использовать бетон в работе на сжатие, а стальные стержни – при работе на растяжение. 2. Укрепление сжатых бетонных конструкций Пример разрушения бетонной балки Факторы, позволяющие существовать железобетону как материалу 1. При твердении происходит прочное сцепление арматуры с бетоном, и оба материала под нагрузкой деформируются совместно; 2. Сталь и бетон имеют почти одинаковые коэффициенты линейного температурного расширения (бетон – 1 10-5 – 1.5 10-5, сталь – 1.2 105). При нагреве и охлаждении не возникает опасных напряжений и не происходит проскальзывание арматуры относительно бетона; 3. Бетон защищает арматуру от коррозии и высоких температур (при пожарах), обеспечивая необходимую долговечность и огнестойкость. Прочность бетона со временем увеличивается; Понятие предварительно напряженного железобетона Недостаточную прочность бетона на растяжение также было предложено устранить созданием на стадии изготовления конструкции сжимающих усилий в той её зоне, которая от внешней нагрузки будет испытывать растяжение. Предварительное сжатие бетона осуществляет предварительно растянутая высокопрочная арматура, которая, пытаясь укоротиться (восстановиться в своей прежней длине) в условиях сцепления с бетоном, обжимает его. Растяжение в бетоне появится только тогда, когда под действием нагрузки будут погашены созданные искусственным путём сжимающие напряжения. Изгибаемая конструкция с предварительно растянутой арматурой, расположенной в нижней зоне сечения, при укорочении арматуры предварительно выгнется. При нагружении конструкции сначала возникнет так называемое «нулевое» положение, когда растягивающие напряжения от нагрузки в нижней части сечения погасятся сжимающие напряжения от предварительного обжатия, а лишь затем конструкция начнёт прогибаться, при достижении уровня R bt в бетоне появятся первые трещины. Поэтому такая конструкция по сравнению с аналогичной ненапряжённой конструкцией имеет повышенную трещиностойкость (работает без трещин или с ограниченным по ширине их раскрытием) и меньшие прогибы. Прочность же обеих конструкций практически одинакова, поскольку предельные напряжения в арматуре и бетоне в момент разрушения равны их прочностям (временным сопротивлениям) растяжения а арматуре и сжатия в бетоне. В 1886 г. американец П.Х. Джексон испытал две железобетонные балки - обычную армированную и с предварительно натянутой арматурой . Опыты оказались неудачными. Все предполагаемые преимущества предварительно напряжённой балки не подтвердились! П.Джексон не учёл потери предварительного напряжения в арматуре В 1888 г. немец В. Дёринг запатентовал способ натяжения арматуры на упоры формы. Он заключается в следующем. До бетонирования конструкции арматуру заводят в форму, один конец её закрепляют в упоре, другой натягивают домкратом (механический способ) до заданного контролируемого напряжения. После приобретения бетоном так называемой передаточной прочности (около 70...80 % проектной) арматуру отпускают с упоров. Она, пытаясь восстановить упругие деформации, в условиях сцепления с бетоном должна обжать окружающий бетон. Способы создания предварительного напряжения Натяжение на упоры Натяжение на бетон. Методы создания предварительного напряжения: • Механический; • Электротермический; • Электротермомеханический; В 1928 г. началось современное развитие предварительно напряженного бетона усилиями французского инженера Эжена Фрейссине (Eugène Freyssinet, 1879-1962), который начал использовать высокопрочную стальную проволоку для предварительного напряжения. Такая арматура имела прочность на разрыв до 18 00 МПА и предел упругости более 12 600 кг/см². Преимущества предварительно напряженных железобетонных конструкций: 1. Высокая трещиностойкость. 2. Пониженная ширина раскрытия трещин. 3. Повышенная жёсткость конструкции. 4. Возможность применять высокопрочную арматуру и бетон Недостатки предварительно напряженных железобетонных конструкций: 1. Повышенная трудоемкость и стоимость изготовления; 2. Опасность образования дополнительных трещин при неравномерном обжатии; 3. Опасность местного разрушения железобетонных конструкций от слишком высоких напряжений обжатия (продольные трещины); 4. Возможность возникновения нежелательных напряжений при транспортировке и монтаже. 5. Повышенная склонность коррозии арматуры. Гидравлический домкрат натяжения арматуры Зажимы для напрягаемой стержневой арматуры Анкеры одноразового пользования при натяжении стержневой арматуры: 1 – напрягаемый стержень; 2 – обжатая шайба; Зажимы для напрягаемой канатной и проволочной арматуры Анкер с конической пробкой Предварительное напряжение Предварительное напряжение железобетонных конструкций позволяет: • Повысить трещиностойкость, • Уменьшить ширину раскрытия трещин; • Повысить жёсткость конструкций (т.е. уменьшить прогибы); На прочность конструкции предварительное напряжение арматуры (предварительное обжатие) практически не влияет. Характер работы обычных (об.) и преднапряженных (п/н) балок под нагрузкой sp sp 0, 3 Rsn При высоких предварительных напряжениях в арматуре (близких к нормативному сопротивлению арматуры) возникает опасность разрыва, в горячекатаной – опасность развития значительных остаточных деформаций. Чтобы этого не произошло при натяжении арматуры должно соблюдаться условие sp sp Rsn По нормам СП 63.13330-2018: σsp 0.9·Rsn - для горячекатаной и термомеханически упрочненной арматуры; σsp 0.8 · Rsn - для холоднодеформированной арматуры и арматурных канатов. Потери предварительных напряжений в арматуре Потери предварительных напряжений в арматуре Первые потери Это потери, которые происходят до передачи усилий натяжения на бетон. 1. Потери от релаксации напряжений в арматуре Для арматуры классов А600 - А1000 Механический способ натяжения Электротермический способ натяжения sp1 . Для арматуры классов Вр1200 - Вр1500, К1400, К1500 Механический способ натяжения sp 0.1sp sp1 0.1 sp 2.0; sp1 0.03 sp . sp1 0.22 R sn Электротермическ ий способ натяжения sp1 0.5 sp 2. Потери от температурного перепада sp2 (МПа). t (°C), - разность температур натянутой арматуры в зоне нагрева и устройств, воспринимающих усилие натяжения при пропаривании или прогреве бетона. sp 2 1, 25 t При отсутствии точных данных по температурному перепаду допускается принимать t = 65 °С. 3. Потери от деформации стальной формы (упоров) sp3 возникают при неодновременном натяжении арматуры на форму определяют по формуле sp 3 n 1 l Es 2n l где n - число стержней (групп стержней), натягиваемых неодновременно; l - сближение упоров по линии действия усилия натяжения арматуры, определяемое из расчета деформации формы; l - расстояние между наружными гранями упоров. При отсутствии данных о конструкции формы и технологии изготовления допускается принимать sp3 = 30 МПа. При электротермическом способе натяжения арматуры потери от деформации формы не учитываются. 4. Потери от деформации анкеров натяжных устройств sp4 Потери от деформации анкеров натяжных устройств при натяжении арматуры на упоры и бетон определяют по формуле l sp 4 Es l При отсутствии данных допускается принимать l = 2 мм. При электротермическом способе натяжения арматуры потери от деформации анкеров не учитывают. 4. Потери от трения о стенки каналов или поверхность конструкции sp7 При натяжении арматуры на бетон потери от трения о стенки каналов или поверхность конструкции определяют по формуле . Вторые потери Это потери напряжения, происходящие после обжатия бетона. 5. Потери от усадки бетона sp5 sp 5 b , sh Es где b,sh - деформации усадки бетона, значения которых можно приближенно принимать в зависимости от класса бетона равными: • 0,0002 - для бетона классов В35 и ниже; • 0,00025 - для бетона класса В40; • 0,0003 - для бетона классов В45 и выше. 6. Потери от ползучести бетона sp6 sp6 0.8 b ,cr bpj ysj2 A red 1 0.8 b ,cr 1 spj 1 I red где b,cr - коэффициент ползучести бетона; ysj - расстояние между центрами тяжести сечения рассматриваемой группы стержней напрягаемой арматуры и приведенного поперечного сечения элемента; Ared, Ired - площадь приведенного сечения элемента и ее момент инерции относительно центра тяжести приведенного сечения; spj - коэффициент армирования, равный Aspj/A, где A и Aspj - площади поперечного сечения соответственно элемента и рассматриваемой группы стержней напрягаемой арматуры. bpj - напряжения в бетоне на уровне центра тяжести рассматриваемой j-й группы стержней напрягаемой арматуры, определяемые по формуле: bp где P1 Ared P1 e0 p y I red My I red P(1) - усилие предварительного обжатия с учетом первых потерь; M - изгибающий момент от внешней нагрузки, действующей в стадии обжатия (собственный вес элемента); e0p - эксцентриситет усилия P(1) относительно центра тяжести приведенного поперечного сечения элемента; y - расстояние от центра тяжести приведенного сечения до рассматриваемого волокна. Тема 3 Материалы железобетона БЕТОН Бетон – искусственный каменный материал, получаемый в результате твердения бетонной смеси. Бетон Вода Специальные добавки: Мелкий заполнитель (песок) • • Крупный заполнитель Вяжущее: Естественный: Искусственный: • щебень; • гравий; • ракушечник; • пемза и др. • керамзит; • шлак и др. • цемент; • известь; • гипс и др. пластификаторы; ускорители или замедлители твердения и др; керамзит щебень Шлаковый щебень гравий Фрагмент бетонного образца Важной характеристикой бетона является W/C (водоцементное отношение) - отношение количества воды к количеству цемента в единице объема бетонной смеси. • для реакции гидротации цемента (химического соединения воды с цементом - W/C = 0,2; • жесткие бетонные смеси (заполняющие формы после виброуплотнения ) - W/C=0,3-0,4; • подвижные бетонные смеси W/C=0,5-0,6. 1. Структура бетона неоднородна и зависит от большого числа факторов: •зернового состава, •водо-цементного отношения, •условий твердения, •степени гидратации цементного камня. 2. Бетон представляет собой капиллярно-пористый материал, в котором присутствуют все три фазы: •твердая; • жидкая ; • газообразная. 3. Цементный камень состоит из кристаллического сростка и наполняющей его вязкой массы – геля. Сочетания упругой и вязкой составляющей дают бетону свойства упруго-пластично-ползучего тела. 4. Бетон является анизотропным материалом (различные свойства в различных направлениях). Классификация бетонов По назначению: • • Конструкционные (для несущих и ограждающих конструкций); Специальные (жаростойкие, радиационностойкие, химически стойкие и др.) По структуре: • • • • • Плотный бетон (обычный); Крупнопористый (только крупный заполнитель); Мелкозернистый (только мелкий заполнитель); Поризованный; Ячеистый. По плотности: • • • • Особо тяжелые, крупный заполнитель, например, сульфат бария (барит), магнитный железняк, (магнетит), гематит (красный железняк), лимонит (бурый железняк), чугунный скраб (шлаки), свинцовая дробь, > 2600 кг/м3 (до 45006500 кг/м3 ); Тяжелые = 2200…2500 кг/м3; Облегченные = 1800…2200 кг/м3; Легкие = 500…1800 кг/м3; Чем выше плотность бетона, тем выше его прочность. Марка бетона по средней плотности D гарантирует среднюю массу бетона в кг/м3. Она назначается для конструкций, к которым кроме требований по прочности предъявляются требования по теплоизоляции . Бетон Легкий бетон Марки по средней плотности D800; D900; D1000; D1100; D1200; D1300; D1400; D1500; D1600; D1700; D1800; D1900; D2000 Ячеистый бетон D500; D600; D700; D800; D900; D1000; D1100; D1200 Поризованный бетон D800; D900; D1000; D1100; D1200; D1300; D1400 Классификация бетона (продолжение) По виду вяжущего: • • • • • Цементные; Полимерцементные; На известковом вяжущем (силикатные); На гипсовом вяжущем; На специальных вяжущих; По виду заполнителя: • • • На плотных естественных заполнителях (гравий, щебень); На пористых заполнителях (керамзит); На специальных заполнителях (удовлетворяющих требованиям по биологической защите, химической стойкости, жаростойкости и т.д.) Классификация бетона (продолжение) По зерновому составу: • Крупнозернистые (без мелкого заполнителя); • С крупным и мелким заполнителем (обычные); • Мелкозернистый (только с мелким заполнителем). По способу твердения: • Естественного твердения; • Бетон, подвергнутый тепловлажностной обработке при атмосферном давлении (пропаривание) (100 град.С); • Бетон, подвергнутый автоклавной обработке при повышенном давлении.(175-190°С и давлении 0,9-1,3 МПа). Свойства бетона Под водонепроницаемостью бетона понимают его способность не пропускать воду. Для резервуаров, напорных трубопроводов и т.п. назначается марка по водонепроницаемости (от W2; W4; W6; W8; W10; W12 для легкого бетона и W2 W12; W14; W16; W18; W20 для тяжелого бетона ). Это число означает давление воды в кг/см2, при котором еще не происходиn её просачивание через цилиндр высотой и диаметром 150 мм. Под морозостойкостью бетона понимается способность материала в увлажненном состоянии сопротивляться разрушающему воздействию попеременного размораживания и оттаивания. Марки бетона по морозостойкости назначаются F50; F75; F100; F150; F200; F300; F400; F500 для легкого бетона и F50-F500; F600; F700; F800; F1000 для тяжелого бетона. Это число характеризует количество выдерживаемых циклов попеременного замораживания и оттаивания в водонасыщенном состоянии, без снижения прочности более чем на 15 % и без видимых разрушений. Жаростойкость – это способность бетона сохранять прочность при длительном воздействии высоких температур (выше 200 С). Схемы крепления и герметизации образцов при испытаниях на водонепроницаемость Свойства бетона Огнестойкость, измеряемая в часах, - это способность бетона сохранять прочность при воздействии открытого огня (1000…1100 С). Для конструкций, работающих при высоких температурах, используются бетоны на заполнителях с малым коэффициентом температурного расширения (шамот, металлургические шлаки и т.п.) и на глиноземистом цементе или на жидком стекле со специальными добавками. Такие бетоны способны выдержать длительное действие температуры до 1200 С. Коррозионная стойкость – это способность бетона не вступать в химическую реакцию с окружающей средой. Для бетонов, работающих в агрессивных средах (газы, кислоты, щелочи) используются полимерные вяжущие (поливинилхлорид, поливинилацетат и др.) Марка по самонапряжению – это среднее значение предварительного напряжения сжатия (самонапряжения) напрягающего бетона, МПа, в возрасте 28 сут., создаваемого в результате его расширения в условиях упругого ограничения деформаций, с жесткостью, соответствующей жесткости стальной арматуры при коэффициенте осевого продольного армирования μ= 0,01 и модуле упругости Es = 200000 МПа (Sp 0.6; Sp 0.8; Sp 1; Sp 1.2; Sp 1.5; Sp 2; Sp 3; Sp 4; Sp 5) Специальные виды бетона Плотный силикатный бетон; Ячеистый бетон Жаростойкий бетон Кислотостойкий бетон Полимербетон Самонапрягающийся бетон Прочность бетона – это способность сопротивляться воздействию внешних сил, не разрушаясь. Нарастание прочности бетона на портландцементе при положительной температуре твердения (около 15 С) и во влажной среде: Rt 0.7 R lg t где R – временное сопротивление сжатию в возрасте 28 дней, t – время твердения. Кубиковая прочность – это временное сопротивление R эталонных кубов, размером 150150150 мм (прочность зависит от размеров образца) хранящихся и испытанных в стандартных условиях: при температуре (202С), влажности 90-100%, на 28 день твердения и определяемое по формуле: R F A где F – разрушающая нагрузка в Н, А – средняя рабочая прочность образца (мм2), - переводной коэффициент, зависящий от размеров образца (размер ребра 100 мм = 0.95; 150 мм = 1.0; 200 мм = 1.05). Характер разрушения бетонных кубов: при трении по опорным плоскостям при отсутствии трения 1 – сила трения Призменная прочность – это временное сопротивление Rb осевому сжатию призмы с отношением высоты призмы h к размеру a квадратного основания равным 4. График зависимости призменной прочности бетона от отношения размеров испытываемого образца: Размеры стандартных призм - 150150600 мм При отношению высоты призмы к стороне основания h/a 4 влияние сил трения исчезает, и прочность становится постоянной и равной 0.75 R. Влияние гибкости бетонного образца сказывается при отношении h/a 8. Эмпирическая зависимость между призменной и кубиковой прочностью бетона: Rb 0.77 0.001 R R Как можно увеличить сопротивление бетона сжатию? - косвенное армирование Образцы после испытаний: а – бетонные призмы, б – образцы, армированные продольной арматурой, в – образцы, армированные хомутами Прочность бетона на осевое растяжение Схема испытаний на сжатие цилиндров Прочность бетона на осевое растяжение Схема испытаний на изгиб бетонных призм Прочность бетона на осевое растяжение Прочность бетона на растяжение приближенно может определяться по эмпирической Формуле, как функция кубиковой прочности бетона: Прочность бетона на растяжение приближенно в 10-20 раз меньше прочности на сжатие. Прочность бетона при срезе и скалывании. Чистый срез – разделение элемента на 2 части по сечению, к которому приложены перерезывающие силы. При срезе распределение напряжений по высоте сечения полагается равномерным. Временное сопротивление бетона при срезе определяется по формуле: R sh 0.7 R b R bt Чистое скалывание – взаимное смещение (сдвиг) частей элемента между собой под действием скалывающих (сдвигающих) усилий. Скалывающие напряжения по высоте меняются по квадратной параболе. Временное сопротивление срезу и скалыванию при изгибе в 1.5 - 2 раза больше Rbt. Схема испытаний на срез Схема испытаний на скалывание Прочность при местном сжатии имеет место, когда нагрузка действует не всю площадь элемента, а на ее часть. В этом случае загруженная часть обладает большей прочностью, чем Rb, поскольку окружающий бетон играет роль обоймы R b , loc b R b где b 0 .8 Ab,max Ab,loc где Ab,loc1 – площадь смятия; Ab,max – расчетная площадь, включающая площадку смятия и дополнительный окружающий участок. Повысить прочность на местное сжатие можно установкой косвенной арматуры. Зависимость прочности от характера изменения нагрузки во времени Предел длительного сопротивления бетона – это наибольшие статические неизменные во времени напряжения, которые от может выдерживать неограниченно долгое время без разрушения. При длительном действии нагрузки бетон разрушается при меньших напряжениях вследствие развития пластических деформаций. R lg t Rbl 0, 71 lg t 0,9 Rb lg 28 где t – время в сутках Предел выносливости или прочность бетона при многократно повторных нагрузках (подвижных или пульсирующих) нагрузках Rr – это напряжение, при котором количество циклов нагружения и разгрузки, необходимых для разрушения образца составляет не менее 2 млн. циклов. b Прочность бетона при статическом и динамическом нагружении Прочность бетона при статическом и динамическом нагружении Классы бетона по прочности Класс бетона «B» по прочности на осевое сжатие – это среднестатистическое значение временного сопротивления сжатию Rm (в МПа) эталонных образцов (кубов с ребром 15 см), изготовленных и испытанных через 28 суток хранения при температуре 202С в соответствии с государственным стандартом с обеспеченностью 0.95. Нормами установлены следующие классы бетона на осевое сжатие: • Для тяжелых бетонов: B3.5, B5, B7.5, B10, B12.5, B15, B20, B25, B30, B35, B40, B45, B50, B55, B60, В70, В80, В90, В100; • Для легких бетонов (в зависимости от плотности): B2.5, B3.5, B5, B7.5, B10, B12.5, B15, B20, B30, B35, B40. Класс бетона «Bt» по прочности на осевое растяжение – это среднестатистическое значение временного сопротивления растяжению Rmt (в МПа) эталонных образцов, испытанных через 28 суток хранения при температуре 202С в соответствии с государственным стандартом с обеспеченностью 0.95. - Установлены следующие классы бетона на растяжение: для тяжелого бетона - Bt0.8, Bt1.2, Bt1.6, Bt2, Bt2.4, Bt2.8, Bt3.2; Вt3,6; Вt4,0; для легкого бетона - Вt0,8; Вt1,2; Вt1,6; Вt2,0; Вt2,4; Вt2,8; Вt3,2. Различие между маркой и классом бетона B 0.0764 M Зачем ввели понятие КЛАСС бетона вместо МАРКА бетона Тема 4 Арматура Основное назначение арматуры – воспринимать растягивающие усилия при изгибе, внецентренном сжатии, центральном и внецентренном растяжении, а также для усиления бетона сжатой зоны изгибаемых элементов, а также сжатых элементов с малыми или случайными эксцентриситетами. Требуемая площадь сечения рабочей арматуры определяется по расчету на действие внешних нагрузок. Коэффициент армирования это отношение площади арматуры к площади сечения бетона: As 100% Ab Конструктивная арматура устанавливается без расчета. Распределительная арматура предназначена для более равномерного распределения усилий между арматурными стержнями. Монтажная арматура применяется для обеспечения проектного положения рабочей арматуры при бетонировании. Дополнительные функции конструктивной арматуры: • • • восприятие усилий от усадки и ползучести бетона; восприятие температурных напряжений; восприятие и местных напряжений, от сосредоточенных сил и т.д. Косвенное армирование – это частое расположение поперечной арматуры, способствующее значительному повышению несущей способности центрально сжатого элемента. Классификация арматуры Классификация стали по содержанию углерода: • Низкоуглеродистая (содержание углерода от 0.09-0.2%); • Среднеуглеродистая (0.25-0.6%) (в арматуре и машиностроении) • Высокоуглеродистая (0.6-1.2%) (инструментальная промышленность); По способу изготовления. • Горячекатаная стержневая ; • Холоднотянутая. По наличию преднапряжения : • Напрягаемая (подвергаемая предварительному натяжению). • Ненапрягаемая; По химическому составу стали. Марка стали – условный показатель, характеризующий сталь по химическому составу. Для обозначения добавок используются буквы: Г – марганец, С – кремний, Х – хром, Т – титан, Ц – цирконий, Ю – алюминий, Р – бор, А – азот. Арматурная сталь марки 20ХГ2Т содержит 0.2% углерода, Х хрома от 0.3 до 1%, Г марганца до 2%, Т титана до 1%. По форме поверхности : • Периодического профиля (винтовая нарезка, в елочку, серповидного профиля); • Гладкая (А240). На поверхности гладкой арматуры также устраиваются вмятины для увеличения сцепления арматуры с бетоном. а – стержневая класса А300 (А-II); б – то же классов А400 (А-III), А600 (AIV), A800 (A-V), A1000 (A-VI); в –стержневая с серповидным профилем (А500С); г – холоднотянутая проволока. Свариваемость арматуры – это способность давать надежные и прочные соединения стержней любым методом сварки: ручной дуговой, контактной точечной, ванной. Пластичность арматуры - способность без разрушения получать большие остаточные деформации. Хладноломкость арматуры – склонность к хрупкому разрушению под напряжением при отрицательных температурах (ниже -30). Прочностные характеристики арматуры: • Физический предел текучести (для мягких сталей) y • (т ); • Условный предел текучести (для высокопрочных сталей) 0.2 (имеется в виду остаточная дефомация 0,2%); • Предел прочности (сопротивление при разрыве) u (пч ) Диаграммы - при растяжении арматурной стали: Три типа диаграммы деформирования арматурных сталей Тип 1 – классы с физической площадкой текучести (А240, А300, А400). Тип 2 – классы с условной площадкой текучести (А500, А600, А800). Тип 3 – высокопрочная арматура (Вр1200-Вр1600, К1400-К1900, А1000). При действии многократно повторяющейся нагрузки величина предела текучести стали снижается, а разрушение приобретает хрупкий характер. Это явление носит название усталости стали. Коэффициент асимметрии цикла s s , min s , max Предел выносливости – это прочность, при которой не наблюдается хрупкого разрушения стали при числе циклов n = 2 млн. раз. Диаграмма мягкой стали при однократном кратковременном динамическом воздействии Классы арматуры Для железобетонных конструкций применяются следующие виды арматуры: • Горячекатаная гладкая и периодического профиля с постоянной и переменной высотой выступов (кольцевой и серповидный профиль) диаметром 6-40 мм% • Термомеханически упрочненная периодического профиля (кольцевого и серповидного) диаметром 6-40 мм; • Холоднодеформированная периодического профиля диаметром 3-12 мм; • Арматурные канаты диаметром 6-15 мм. Обозначения классов: А – горячекатаная и термомеханически упрочненная гладкая и периодического профиля (стержневая арматура); В – холоднодеформированная гладкая арматура (проволочная арматура); Вр –холоднодеформированная арматура периодического профиля (проволочная арматура); К – арматурные канаты; Применение классов арматуры Прочность арматуры растёт быстрее её стоимости Для конструкций без предварительного напряжения 1. В качестве рабочей продольной арматуры используют: • стержневую периодического профиля А400, А500, А600; • холоднодеформированную (проволочную) В500, Вр500 (в сварных сетках и каркасах); 2. Для поперечного и косвенного армирования используют : • стержневую А240, А400, А500; • проволочную В500, Вр500; Для предварительно напряженных конструкций. 1. В качестве напрягаемой арматуры используют : • горячекатаную А600, А800, А1000 (длина до 13 м); • холоднодеформированную периодического профиля Вр1200, Вр1300 Вр1400, Вр1500, Вр1600 (длина не ограничена); • канатную семипроволочную К1400, К1500, К1600, К1700, К1800, К1900(длина не ограничена); 2. В качестве ненапрягаемой арматуры используют : • горячекатаную А240, А400, А500, А600; • холоднодеформированную В500, Вр500. Для арматуры класса А и В класс – это гарантированное значение предела текучести (с округлением) с обеспеченностью не менее 0.95, определяемое в соответствии со стандартом. Для высокопрочной арматуры класс – это гарантированное значение условного предела текучести (равного значению напряжений, соответствующих остаточному относительному удлинению 0.2%) с обеспеченностью не менее 0.95 определяемому по соответствующим стандартам. Прочность арматуры при сжатии принимается равной прочности при растяжении но не более 400 Мпа при кратковременном действии нагрузки из условия равенства предельных деформаций арматуры и бетона. bc,u sc bc,u 0.002 sc sc Es bc,u Es 0.002 2 105 400 МПа Канаты и проволочные пучки Натяжение канатной арматуры на бетон конструкции моста Преимущества использования высокопрочной проволоки и канатов в преднапряженных конструкциях: 1. Высокая прочность достигается за счет использования углеродистой стали и многоступенчатого термомеханического упрочнения без использования дефицитных легирующих добавок. 2. Возможность поставки любой требуемой длины. 3. Возможность создания преднапряженных элементов любого очертания с широким диапазоном разрывного усилия. Недостатки использования высокопрочной проволоки и канатов : 1. Себестоимость выше, чем у стержневой арматуры из-за высокой стоимости технологических процессов. 2. Разупрочнение арматуры при натяжении электротермическим способом. 3. Значительная трудоемкость при применении в изделиях длиной 6-9 м. при натяжении на упоры (при агрегатно-поточной или конвейерной технологии) 4. Необходимость использования высокопрочного бетона (не ниже В30). Деформативность арматуры Деформативность арматуры оценивается через: • относительное удлинение при разрыве; • величину угла загиба в холодном состоянии, который стержень может выдержать без хрупкого разрушения; • число перегибов проволоки в холодном состоянии; • ползучесть стали; • релаксацию стали. Релаксация – уменьшение напряжений при отсутствии деформаций (неизменной длине). Горячекатаные мягкие низколегированные стали обладают малой релаксацией. Значительной релаксацией обладает проволока, упрочненная вытяжкой и термически упрочненная арматура. 50-60% проявляются в течении первого часа (важно для предварительно напряженных конструкций); • модуль упругости арматуры (для всех сталей приводится в СП по проектированию предварительно напряженных ЖБК и ЖБК без напряжения); Арматурные изделия d Арматурные сетки Плоские Рулонные , c1 u c2 L Dv c1 c 2 AL Параметры сеток в условных обозначениях: C du k где С – сетка; D – диаметр продольных стержней; v – шаг продольных стержней; d – диаметр поперечных стержней; u – шаг поперечных стержней; А – ширина сетки; L – длина сетки; с1, с2 - свободные концы продольных стержней, k – свободные концы поперечных стержней; A v Вязаные k Сварные D k Арматурные сетки Арматурные сетки Тяжелые (стержни в одном направлении 12 мм и больше) Легкие рулонные (продольные и поперечны стержни от 3 до 10 мм включительно) Легкие арматурные сетки (ГОСТ 23279-2012) Тип 4 – легкие с поперечными стержнями на всю ширину сетки; Тип 5 - легкие со смещенными поперечными стержнями; Тяжелые арматурные сетки (ГОСТ 23279-2012) Тип 1 – тяжелые с рабочей арматурой в продольном направлении, диаметр которой больше диаметра распределительной арматуры; Тип 2 - тяжелые с рабочей арматурой в обоих направлениях; Тип 3 – тяжелые с рабочей арматурой в поперечном направлении, диаметр корой больше диаметра распределительной арматуры. Арматурные каркасы. d c1 v c1 d2 c S S S d1 Размеры С и С1 концевых выпусков продольных или поперечных стержней должны быть не менее 0.5d1+d2 или 0.5d2+d1, и не менее 20 мм где d1 и d2 – диаметры стержней во обоих направлениях. Соотношение диаметров свариваемых поперечных и продольных стержней принимают не менее 0.25…0.33. Закладные детали Закладные детали с нормальными анкерами: а - без усилений; б - с анкерными пластинами; в - с высаженными головками; г - с двумя пластинами (типа «закрытый столик») Закладные детали усложненной конструкции: а - с жесткими анкерами; б - с приваркой уголков Применяются при действии больших нагрузок Закладные детали с нормальными и наклонными анкерами а-в - с наклонными анкерами, приваренными внахлестку, и нормальными; г - с наклонными анкерами, приваренными под слоем флюса Штампованные закладные детали 1 - участок закладной детали, выполняющий функцию пластины; 2 - полосовой анкер Применяются при действии сдвигающей и отрывающей силы при Q>N Применяются при действии небольших нагрузок Закладные детали: расчетные конструктивные Конструктивные требования: • Толщина стальных листов для закладных деталей не менее 6 мм; • Толщина полок фасонного проката не менее 5 мм; • Для нерасчетных соединений данные величины снижаются не более чем на 1 мм во избежание прожога. • Анкерные стержни рассчитываются на восприятие растягивающих усилий и усилий среза. Их длина принимается по расчету, но не менее 15d для анкеров без анкерных устройств на концах и не менее 10d при наличии анкерных устройств. • Для возможности механизированного заглаживания поверхности изделия закладные детали заглубляют в бетон не менее, чем на 5 мм. Сварные соединения арматуры. а) контактный стык (при разнице в свариваемых диаметра не более 15% и наименьшем диаметре 10 мм); б) ванный в инвентарной форме; в) двухсторонний шов с накладками; г) одностонний шов с накладками; д) нахлесточный шов при соединении двух стержней; е) нахлесточный при соединении стержня с пластиной; ж) тавровый при соединении стержня с перпендикулярной пластиной; з) контактно-точечный при соединении пересекающихся стержней сеток и каркасов и) ширина и высота сварного шва. Сварные соединения арматуры Ванная сварка арматуры Соединение арматуры внахлест Соединение арматуры внахлест (перепуск арматуры) Определяется по формуле СП 52-101-2003 Механическое соединение арматуры Резьбовые а - сжато-растянутый стык с контргайками; б - сжатый стык с контргайками; в - сжатый (контактный) стык; г - два вида концевых анкеров винтовой арматуры; 1 - соединительная муфта; 2 - контргайка; 3 щель для контроля контакта стержней; 4 - анкерная гайка; 5 - анкерная шайба Болтовые Обжимные Типы муфт: резьбовая с конической резьбой, обжимная, резьбовая с цилиндрической резьбой Соединение арматуры колонны с помощью винтовых муфт Соединение арматуры колонны с помощью обжимных муфт Опрессовка обжимных муфт Болтовые муфты Специальные виды арматуры Перекрытия по профилированному настилу Конструкция монолитного перекрытия по СПН с вертикальными стержневыми анкерами: 1 монолитный бетон; 2 - арматурная сетка; 3 - стальной профилированный настил; 4 - вертикальный анкер; 5 – прогон. Стальной профилированный настил, рекомендуемый для монолитных перекрытий Преимущества: снижение расхода стали на 15% на балки; сокращение трудозатрат при строительстве на 25-40% по сравнению с традиционными монолитными перекрытиями; сокращение сроков строительства на 25 %; уменьшение массы перекрытия на 30-50% по сравнению с традиционными перекрытиями; уменьшение строительной высоты на 10%; увеличение жесткости перекрытий при действии горизонтальных нагрузок; возможность размещения коммуникаций в гофрах; отсутствие деревянной опалубки; повышение безопасности труда и пожарной безопасности на стадии монтажа. Недостатки: • Профилированный настил остается в перекрытии в качестве несъемной опалубки; • Приходится проводить дополнительные мероприятия по повышению огнестойкости таких перекрытий. • Требуются дополнительные мероприятия по обеспечению надежного сцепления профнастила с бетоном. ЖБК с жесткой арматурой Несущая арматура – это арматура в виде прокатных двутавров, швеллеров, уголков 1 – жесткий профиль; 2 – арматурные стержни; 3 – соединительные планки. Трубобетон – это комплексная конструкция, состоящая из стальной трубы и бетонного ядра, работающего совместно. Достоинства: • Прочность бетонного ядра, стесненного стальной оболочкой как обоймой в 2 раза больше, чем прочность обычного бетона. • Исcледованиями установлено, что при твердении бетона в трубе из-за отсутствия влагообмена с окружающей средой вместо его усадки происходит набухание, что создает благоприятные условия для его работы. • Деформации нелинейной ползучести исчезают в изолированном бетоне через 7-8 суток, а в обычном через 20-30 суток. • Повышается коррозионная стойкость трубобетонных элементов, уменьшается гибкость, увеличивается местная устойчивость стенок трубы. • Стоимость трубобетонных конструкций ниже, чем аналогичных железобетонных и стальных. Недостатки: • Многими исследователями трубобетона отмечалось, что труба начинает работать как обойма лишь в стадии близкой к разрушению бетона, до этого труба является лишь опалубкой, если ее не включать в работу специальными мероприятиями. • Более низкая огнестойкость трубобетонных колонн. Неметаллическая арматура Стеклопластиковую арматуру получают из тонких стекловолокон, объединяемых в арматурный стержень с помощью связующих синтетических смол. Базальтовая арматура – это арматура, изготовленная из базальта (горной породы), которая после измельчения под нагревом превращается в нити. Углепластиковая арматура – это специализированный материал, состоящий из основы - углеродного волокна, и составляющей – термореактивной синтетической смолы, которая является связующей. Достоинства неметаллической арматуры: • • • • • • • • Долгий срок службы вследствие устойчивости к коррозионным процессам. Хорошее сцепление с бетоном. Небольшой удельный вес Низкая теплопроводность, что способствует энергосбережению. Высокая прочность на разрыв (до 1800 Мпа). Легкость; Радиопрозрачность, магнитоинертность; Коррозионная стойкость; Недостатки: • • • • Низкая огнестойкость; Склонность к разрушению от щелочных реакций; Старение (снижение прочности во времени); Низкий модуль упругости и, как следствие, высокая деформативность конструкций. • Отсутствие в нашей стране на настоящий момент нормативной базы и надёжного расчётного аппарата Тема 5 Совместная работа арматуры и бетона Основные факторы, обеспечивающие сцепление арматуры с бетоном: • Механическое зацепление арматуры за бетон ( 75%); • Силы трения на поверхности арматуры ( 15%) ; • Склеивание поверхности арматуры с бетоном( 10%). Факторы, влияющие на величину сцепления 1. Прочность бетона на растяжение; 2. Расположение стержня в бетонном сечении; 3. Площадь поверхности арматуры, поэтому предпочтительно ставить несколько тонких стержней вместо одного толстого, например, 4Ø10 и 1Ø20 имеют одинаковую площадь 3,14 см2, на разную площадь поверхность сцепления; 4. Вид поверхности арматуры; 5. Косвенное армирование; Напряженное состояние на поверхности контакта арматуры с бетоном при выдергивании l an c, max N m s N s y A s m u lan N Базовая длина анкеровки l 0an R s As R bond u s As и us – площадь поперечного сечения и периметр анкеруемого стержня; Rbond – расчетное сопротивление сцепления арматуры с бетоном. Rbond 1 2 Rbt Rbt – расчетное сопротивление бетона осевому растяжению; 1 – коэффициент, учитывающий влияние вида поверхности арматуры, 2 – коэффициент, учитывающий влияние диаметра арматуры. Длина анкеровки: lan l0an A s ,cal A s ,ef As,cal – площадь арматуры требуемая по расчету, As,ef – фактически установленная площадь арматуры, - коэффициент, учитывающий влияние напряженного состояния и конструктивного решения. Совместная работа арматуры и бетона обеспечивает: • • • • Защиту арматуры от коррозии и высоких температур; Равномерность образования трещин в бетоне растянутой зоны; Сохранность повышенной жесткости изгибаемых элементов; Равномерное распределение усилий по длине рабочих стержней и между отдельными стержнями. Усадка железобетона lsb l b l p lb – деформация усадки бетонного образца, lsb – деформация усадки железобетонного образца, lp – деформация усадки предварительно напряженного образца. а) симметрично армированный элемент; б) несимметричное армирование. slb – усадка бетонного образца-близнеца, sb - усадка железобетонного образца, bt – деформации растяжения бетона в железобетонном образце В статически неопределимых конструкциях усадка вызывает дополнительные внутренние усилия, которые могут нарушить целостность конструкции. Во избежание этого протяженные конструкции делят усадочными швами на блоки. Т.к. по внутренним усилиям усадка бетона эквивалентна понижению температуры на 15С, усадочные швы обычно совмещают с температурными и называют температурно-усадочными. Виды железобетона • тяжелый бетон с гибкой арматурой (обычный бетон); • железобетон с жесткой арматурой - арматура в виде прокатных профилей (двутавров, швеллеров и уголков) до отвердения бетонной смеси работает на нагрузку от собственного веса, веса подвешиваемой к ней опалубки и веса бетонной смеси; • легкий железобетон - железобетон, в котором применяется бетон на пористых заполнителях; • армоцемент – это армированный частыми стальными мелкоячеистыми сетками бетон на мелком заполнителе класса В25-В50. На 1 см толщины бетона укладывают не более 4 сеток с ячейками не более 10 мм их проволоки от 0.5 до 1 мм; • фибробетон – это бетон, армированный волокнами в виде обрезков тонкой стальной проволоки, стеклянных или синтетических нитей, составляющих от 1.5 до 3% объема бетона. • армополимербетон - в качестве вяжущего в нем применяют фенолформальдегидные смолы и армируют стальной или неметаллической арматурой. Тема 6 Методы расчета строительных конструкций Расчет по допускаемым напряжениям (действовал до 1938 г.) Расчет по разрушающим усилиям (действовал до 1955 г.) Расчет по предельным состояниям (с 1955 г. по наст. время) РАЗВИТИЕ МЕТОДОВ РАСЧЕТА СЕЧЕНИЙ Расчет по допускаемым напряжениям (действовал до 1938 г.) Основные допущения: 1. Бетон растянутой зоны не работает, а растягивающие напряжения воспринимаются арматурой; 2. Бетон сжатой зоны работает упруго, а зависимость между напряжениями и деформациями линейная (закон Гука). 3. Справедлива гипотеза плоских сечений. 4. Вместо действительного сечения рассматривалось фиктивное сечение, в котором арматура заменялась эквивалентным количеством бетона. Коэффициент приведения: Es Eb В этом случае сечение можно было рассматривать как однородное из материала с одним модулем упругости. A red A A s A s' где A – площадь сжатой зоны бетона поперечного сечения элемента; As – площадь растянутой арматуры, As’ – площадь сжатой арматуры Недостатки метода: 1. Бетон рассматривался как упругий материал. Не учитывались его пластические свойства. 2. Теоретические величины напряжений не соответствовали экспериментальным данным (были завышены), особенно после внедрения легких и высокопрочных бетонов и высокопрочных сталей. 3. Не учитывалась изменчивость нагрузок и материалов. 4. Надежность обеспечивалась только одним коэффициентом запаса, зависящим от материала конструкций. Расчет по разрушающим усилиям (предложен проф. кафедры ЖБК МИСИ А.Ф. Лолейтом и действовал до 1955 г.) Допускаемое усилие определялось делением разрушающего усилия на общий коэффициент запаса прочности. Для изгибаемых элементов M Mu k N Nu ; k Для сжатых элементов Коэффициент запаса устанавливался нормативно в зависимости от причины разрушения конструкции и отношения усилий от длительных нагрузок к усилиям от постоянных нагрузок. Недостатки метода: 1. Использование единого коэффициента прочности, не позволяющего учесть все многочисленные и разнородные факторы, влияющие на работу конструкции. 2. Не было возможности оценить работу конструкции на стадии, предшествующей разрушению. 3. Прогибы при таких методах расчета могли оказаться значительными, так же как и ширина раскрытия трещин. Метод расчета по предельным состояниям разработан проф. кафедры МК МИСИ Н.С.Стрелецким Предельное состояние – это состояние, при котором конструкции перестают удовлетворять предъявляемым к ним в процессе эксплуатации требованиям, т.е. теряют способность сопротивляться внешним нагрузкам или получают недопустимые перемещения или местные повреждения. Предельные состояния делятся на 2 группы: • 1 группа - по несущей способности. Предельное состояние в результате исчерпания несущей способности ,т.е. разрушение материала в наиболее нагруженных сечениях, а также потеря устойчивости некоторых элементов или всей конструкции в целом. Потеря устойчивости: Потеря прочности: положения формы хрупкое, вязкое или иного характера разрушение расчет на выносливость (усталостное разрушение) расчет на устойчивость расчет на опрокидывание, скольжение, всплытие сооружений 2 группа – конструкции не пригодны к нормальной эксплуатации Вследствие: – чрезмерных деформаций и перемещений (прогибы, перекосы, колебания, осадки), – образования трещин (когда трещины не допускаются), – чрезмерного раскрытия трещин (когда трещины допускаются). Коэффициенты надёжности и коэффициенты условий работы В методе предельных состояний применяется системы коэффициентов надежности и коэффициентов условий работы, учитывающая изменчивость нагрузок (в большую сторону) и прочностных характеристик материала (в меньшую сторону): 1. Коэффициент надежности по нагрузке (0,9 f 1,4). Зависит от вида нагрузки и группы предельных состояний; 2. Коэффициент надежности по бетону (для тяжелых бетонов 1,0 b 1,5). Зависит от вида напряженного состояния, вида бетона и группы предельных состояний; 3. Коэффициент надежности по арматуре (1,0 s 1,2). Зависит от класса арматуры и группы предельных состояний. 4. Дополнительные коэффициенты условия работы бетона (для тяжелых бетонов bi 1). Учитывают особенности работы бетона в конструкции, особенности бетонирования, характер загружения, условия эксплуатации и др. 5. Коэффициенты условия работы арматуры (si 1). Учитывает условия работы арматуры в конструкции (продольная арматура, хомуты, отгибы) . Основные источники неопределенности Неопределенности случайного характера 1. Неопределенность нагрузок Неопределенность существует как в величине, так и в характере приложения нагрузки 2. Неопределенность прочностных характеристик Неопределенности неслучайного характера 1. Неопределенность расчетной схемы 2. Неопределенность схемы разрушения 3. Неопределенность условий изготовления и эксплуатации. Расчетные нагрузки и воздействия. Нормативные нагрузки – это нагрузки установленные нормами по заданной заранее вероятности превышения средних значений или по номинальным значениям. Расчетные нагрузки – это нагрузки используемые в расчетах конструкций на прочность и устойчивость. q qn f n где f – коэффициент надежности по нагрузке, принимаемый по СП 20.13330.2016 «Нагрузки и воздействия», n – коэффициент надежности по назначению сооружения, принимаемый по ГОСТ 27751 — 2014 «НАДЕЖНОСТЬ СТРОИТЕЛЬНЫХ КОНСТРУКЦИЙ И ОСНОВАНИЙ» Уровни ответственности: I – повышенный n > 1; II – нормальный уровень ответственности n = 1.0; III – пониженный уровень ответственности n = 0.8; Постоянные – нагрузки, действующие в течение всего периода эксплуатации. Это вес несущих и ограждающих конструкций, вес и давление грунтов для заглубленных сооружений, усилие предварительного обжатия. Временными называются нагрузки, изменяющие в процессе эксплуатации по величине или положению. Длительные - вес стационарного оборудования, нагрузка от массы продуктов, заполняющих оборудование в процессе эксплуатации, пониженное значение снеговых нагрузок, полезных нагрузок, давление жидкостей, газов и сыпучих материал в емкостях, трубопроводах и др. Кратковременные - вес людей, полное значение снеговых нагрузок, ветровые, крановые нагрузки, а также нагрузки, возникающие при монтаже и ремонте конструкций. Особые - сейсмические, взрывные и прочие аварийные воздействия. Одновременное действие постоянных, длительных и кратковременных нагрузок называется основным сочетанием. Особые сочетания складываются их нагрузок из основного сочетания и одной из особых нагрузок. Вероятность одновременного воздействия наибольших нагрузок учитывается коэффициентами сочетаний, принимаемым 1. Расчет конструкций выполняется на действие нагрузок в различных сочетаниях. Одновременное действие постоянных, длительных и кратковременных нагрузок называется основным сочетанием. Вероятность одновременного воздействия наибольших нагрузок учитывается коэффициентами сочетаний. Cm = Pd+(l1 Pl1+l2 Pl2+l3 Pl3+…)+(t1 Pt1+t2 Pt2+t3 Pt3+…), где Pd – постоянная нагрузка, Pl1, Pl2, Pl3…– длительные нагрузки, Pt1, Pt2, Pt3…– кратковременные нагрузки, l1 = 1.0 - коэффициент сочетаний, соответствующий основной по степени влияния длительной нагрузке; l2 = l3 = … = 0.95 - коэффициенты сочетаний для остальных длительных нагрузок t1 = 1,0 - коэффициент сочетаний, соответствующий основной по степени влияния кратковременной нагрузке; t2 = 0,9 - коэффициент сочетаний, соответствующий второй кратковременной нагрузке; t3 = t4 = … = 0,7коэффициенты сочетаний для остальных кратковременных нагрузок Нормативные и расчетные сопротивления бетона Класс бетона по прочности принимается равным наименьшему контролируемому значению временного сопротивления бетона с 95% обеспеченностью. Пусть проведено n опытов. Тогда класс бетона можно определить по формуле: B Rm k R где R m i1 i n - среднее значение временного сопротивления сжатию (математическое ожидание); k 2 n i i i1 n 1 i Ri Rm 1.64 - среднеквадратическое отклонение (или стандарт); - уклонение - показатель надежности для 95 %-ной доверительной вероятности. Нормативное сопротивление бетона при сжатии – это призменная прочность, которая устанавливается в зависимости от класса бетона: R bn B 0.77 0.00125 B Сопротивление бетона осевому растяжению: Rbtn 0.5 k 3 B 2 , (k=0.8 для бетонов до В35, k=0.7 для бетонов выше класса B40) Расчетное сопротивление бетона устанавливается путем деления нормативных сопротивлений на соответствующие коэффициенты надежности: R bn Rb ; bc R btn R bt ; bt bc 1.3 при расчете по несущей способности; bc 1.0 при расчете по пригодности к эксплуатации; bt 1.5 при расчете по несущей способности (для классов по прочности на сжатие); bt 1.3 при расчете по несущей способности (для классов по прочности на растяжение); bt 1.0 при расчете по пригодности к эксплуатации (кроме расчета по образованию трещин с целью их недопущения). Коэффициенты условий работы бетона γb1 - для бетонных и железобетонных конструкций, вводимый к расчетным значениям сопротивлений Rb и Rbt и учитывающий влияние длительности действия статической нагрузки: γb1 = 1,0 при непродолжительном (кратковременном) действии нагрузки; γb1 = 0,9 при продолжительном (длительном) действии нагрузки; Для ячеистых и поризованных бетонов γb1 = 0,85; γb2= 0,9 - для бетонных конструкций, вводимый к расчетным значениям сопротивления Rb и учитывающий характер разрушения таких конструкций; γb3 = 0.85 - для бетонных и железобетонных конструкций, бетонируемых в вертикальном положении при высоте слоя бетонирования свыше 1,5 м, вводимый к расчетному значению сопротивления бетона Rb γb4 - для ячеистых бетонов, вводимый к расчетному значению сопротивления бетона Rb: γb4 = 1,00 - при влажности ячеистого бетона 10 % и менее; γb4 = 0,85 - при влажности ячеистого бетона более 25 %; по интерполяции - при влажности ячеистого бетона свыше 10 % и менее 25 %. Нормативные и расчетные сопротивления арматуры Нормативные сопротивления арматуры принимают равными наименьшему контролируемому значению: для стержневой арматуры, высокопрочной проволоки и арматурных канатов – пределу текучести (физическому или условному); для обыкновенной арматурной проволоки – напряжению, составляющему 75% от временного сопротивления при разрыве. Нормативные сопротивления стали принимаются с надежностью 0.95 Расчетное сопротивление растяжению определяется делением на соответствующий коэффициент надежности по арматуре: Rs Rsn s Коэффициент надежности устанавливается: s = 1.1 для арматуры классов А240, А300, А400. s = 1.15 для арматуры класса А500, А600, А800; s = 1.2 для арматуры класса А1000, В500, Вр1200-Вр1500, К1400, К1500; При расчете по предельным состояниям 2 группы коэффициент надежности принимается равным 1 (кроме расчета по образованию трещин с целью их недопущения). Основные положения расчета Расчет по первой группе предельных состояний Этот расчет гарантирует сохранение несущей способности конструкции с учетом возможной изменчивости нагрузок в большую сторону и прочностных характеристик материалов в меньшую сторону: F Fu S; R bn ; b ; bt ; R sn ; s ; si где F – максимальное расчетное усилие в сечении; Fu – минимальная несущая способность сечения; S – геометрические характеристики сечения; Rbn, Rsn – нормативные сопротивления материалов; b, si, b, bi - коэффициенты условий работы. Физический смысл данного выражения заключается в том, что максимально возможное усилие в сечении элемента должно быть меньше или равно минимально возможной несущей способности сечения. Расчет по второй группе предельных состояний Расчет по второй группе предельных состояний должен гарантировать сохранение эксплуатационных качеств конструкции с учетом изменчивости прочностных и деформационных свойств материалов. Расчет по образованию трещин. Трещины в элементе не появляются, если выполняется условие: F Fcrc Физический смысл: максимально возможное усилие в сечении элемента от действующей нагрузки должно быть меньше или равно усилию, которое может восприниматься сечением перед образованием трещин. Расчет по раскрытию трещин. Если образование трещин по условиям эксплуатации допустимо, но должна быть ограничена ширина их раскрытия, должно выполняться условие: a crc a crc a crc – расчетная ширина раскрытия трещин; [a crc] – предельно допустимая ширина раскрытия трещин. Расчет по перемещениям. При необходимости ограничения деформаций должно выполняться условие: f f где f - расчетная деформация (перемещение), [f] – предельное значение деформаций допускаемое нормами. Тема 7 Стадии напряженно-деформированного состояния железобетонного сечения при изгибе E s bt ; s / Es bt / Ebt ; s bt Es / Ebt ; т.к. в момент до появления первой трещины Ebt 0,5Eb ; bt Rbt , ser , то получаем s 2 Es Rbt , ser 2 Rbt , ser 20 МПА. Eb - x Rb ось симметрии нейтральная ось + s y s 0.2 Положение границы между случаями 1 и 2 устанавливается в зависимости от высоты сжатой зоны x h0 Значение , при котором одновременно происходит исчерпание несущей способности бетона сжатой зоны и растянутой арматуры, обозначают R (относительная граничная (или предельная) высота сжатой зоны). R Случай 1 разрушения R Случай 2 разрушения В железобетонных элементах без преднапряжения из подобия треугольников имеем bc,max xR s ,u h0 xR bc ,max xR 1 R s ,u h0 s ,u bc ,max bc ,max 1 где bc ,max b ,ult 0.0035 bc ,max xR 1 R s ,u h0 s ,u bc ,max bc ,max 1 0,8 s ,u bc ,max . 1 Мягкие стали R s,u s,el s Es x R R h0 0.8 0.8 R 1 s ,el 1 s 700 b,ult Высокопрочные стали с преднапряжением Высокопрочные стали с условным пределом текучести s ,u s 0.002 Rs 400 Es 0.2 Es 0.002 s ,u Rs 400 R 400 sp sp s Es Es Es Rs 400 sp Es R где xR h0 s ,el 0.8 s, el 1 b 2 R s 400 sp Es Особенности работы преднапряженных конструкций Вторая и третья стадии работы такие же, что и в обычных конструкциях, но прогибы и ширина раскрытия трещин меньше. Тема 8 Расчет прочности изгибаемых элементов Изгибаемые элементы – это всевозможные балки, ригели, плиты, фундаменты, стенки резервуаров и многие другие конструкции q=g+v 3 2 1 4 1 – нормальное сечение, по которому произошло разрушение элемента; 2, 3 – нормальные и наклонные трещины, 4 – продольная рабочая арматура. Исчерпание несущей способности изгибаемых элементов может произойти от изгибающего момента M при нулевой поперечной силе Q (по нормальным сечениям), так и от поперечной силы при сравнительно небольшом значении момента M (наклонное сечение). Два случая разрушения изгибаемых элементов Существует два случая разрушения изгибаемых элементов по нормальным сечениям: Случай 1 – в сжатом бетоне и растянутой арматуре достигнуты предельные значения напряжений: Rb и Rs , сжатый бетон и растянутая арматура разрушаются одновременно. Случай 2 – в сжатом бетоне достигнуто напряжение Rb, а в растянутой арматуре вместо Rs действует меньшее напряжение s. Такое разрушение называется хрупким, так в конструкции разрушается только сжатая часть бетона. Положение границы между случаями 1 и 2 устанавливается в зависимости от высоты сжатой зоны x h0 Значение , при котором одновременно происходит исчерпание несущей способности бетона сжатой зоны и растянутой арматуры, обозначают R (относительная граничная (или предельная) высота сжатой зоны). R Случай 1 разрушения R Случай 2 разрушения Основные предпосылки расчета по нормальным сечениям • Внутренние усилия в расчетном сечении элемента определяют для стадии III (стадия разрушения); • Рассматривается сечение, проходящее по трещине в растянутом бетоне, сопротивление бетона растяжению не учитывается; • Сопротивление бетона сжатию представляется напряжениями, равными призменной прочности бетона Rb, а эпюру напряжений принимают прямоугольной; • Растягивающие напряжения в арматуре принимают не более ее расчетного сопротивления Rs, а сжимающие напряжения – не более расчетного сопротивления Rsc. Расчётное сечение Подавляющее большинство физических сечений изгибаемых конструкций можно привести к расчётному тавровому или прямоугольному сечению (кроме круглых и им подобным). Под расчётным сечением подразумевается форма сжатой зоны бетона. Форма расчетного сечения зависит от эпюры моментов: Порядок получения расчетных формул • В точке с максимальным изгибающим моментом проводим мысленно сечение, которое делит элемент на две части, одна из которых отбрасывается и заменяется усилиями, равнодействующая которых приложенными к центру тяжести эпюры напряжений в сжатой зоне бетона и к центру тяжести поперечного сечения арматуры; • Рассматриваются два уравнения равновесия: Mц.т.сжатой зоны Mц.т.As 0 N 0 x - сумма моментов всех сил относительно оси, проходящей через центр усилий в растянутой арматуре или ц.т. сжатой зоны бетона; - сумма проекций всех сил на горизонтальную ось. x a' s3 R s A sp A's A'sp A sp a zs zb h h M R sc A's ' sc A'sp Nb Равнодействующие усилий в сечении: Nb Rb Ab N R A s sc s R s As - в сжатом бетоне; - в сжатой арматуре; N sp sc Asp - в сжатой преднапряжённой арматуре; N s Rs As - в растянутой арматуре; N sp s 3 Rs Asp - в растянутой преднапряжённой арматуре; As Если есть только ненапряженная арматура в растянутой и сжатой зонах То первое уранеие равновесия будет иметь вид: N 0, x Nb N s N s 0, R A R A R A 0. b b sc s s s Из этого уравнения можно определить высоту сжатой зоны бетона сжатой зоны бетона входит в площадь сжатой зоны бетона Ab . (1) x, т.к. высота Второе уравнение равновесия (по моментам) можно записать двумя способами; z ' M 0, M M 0, N z N ц .т.сж.бетона u s b s s M M z M 0. M M 0, N z N ц .т.As u b b s s Получается либо условие прочности по моменту относительно центра тяжести сжатой зоны бетона (2а) M M u Rs As zb ( x) Rsc As zs' ( x ); Либо условие прочности по моменту относительно центра тяжести растянутой арматуры M M u Rb Ab ( x) zb ( x) Rsc As h0 as . h0 h a - рабочая высота сечения; а– расстояние от крайнего растянутого волокна бетона до центра тяжести арматуры (а часто называют защитный слой, хотя по СП 63.13330.2018 защитный слой это a1 , не путать!) a a1 0,5 d - при однорядном расположении арматуры; a a1 0,5 d 0,5 c - при двухрядном расположении арматуры; a1 - толщина защитного слоя бетона по СП 63.13330. (2б) Уравнения (1) и (2) неприменимы, если в растянутой зоне установлено недостаточное количество арматуры, т.к. при появлении первой трещины усилия с растянутого бетона передаются на арматуру, и она может разорваться. Чтобы этого избежать устанавливается минимальный процент армирования. Для изгибаемых элементов величина по СП 63.13330.2018 s ,min As ,min b h0 100% 0,1% Минимальное и максимальное количество арматуры в изгибаемых элементах Конструктивные требования к ЖБК ГЕОМЕТРИЧЕСКИЕ РАЗМЕРЫ КОНСТРУКЦИЙ Минимальные геометрические размеры сечений конструкций должны обеспечивать: - возможность надлежащего размещения арматуры (расстояния между стержнями, защитный слой бетона и т.д., ее анкеровки и совместной работы с бетоном; достаточную жесткость конструкций; необходимую огнестойкость, водонепроницаемость конструкций, тепло- и звукоизоляцию, коррозионную стойкость, радиационную защиту и т.п.; возможность качественного изготовления при бетонировании конструкций. Гибкость lo/h в любом направлении для сжатых элементов прямоугольного сечения не должна превышать: - для железобетонных элементов ≤ 60); - для колонн, являющихся элементами зданий ≤ 35); - для бетонных элементов ≤ 2b). Толщина полок приниматься не менее: - монолитных ребристых перекрытий должна для покрытий – 40 мм; для междуэтажных перекрытий жилых и общественных зданий – 50 мм для междуэтажных перекрытий; производственных зданий – 60 мм. В конструкциях зданий и сооружений следует предусматривать их разрезку температурно-усадочными швами, расстояния между которыми назначают в зависимости от климатических условий, конструктивных особенностей сооружения, последовательности производства работ и т.п. При возможности неравномерной осадки фундаментов следует предусматривать разделение конструкций осадочными швами. ЗАЩИТНЫЙ СЛОЙ БЕТОНА № п/п Условия эксплуатации конструкций здания Толщина защитного слоя бетона, мм, не менее 1 В закрытых помещениях при нормальной и пониженной влажности В закрытых помещениях при повышенной влажности (при отсутствии дополнительных защитных мероприятий) 20 3 На открытом воздухе (при отсутствии дополнительных защитных мероприятий) 30 4 В грунте (при отсутствии дополнительных защитных мероприятий), в фундаментах при наличии бетонной подготовки 40 5 В монолитных фундаментах при отсутствии бетонной подготовки 70 2 25 Дополнительные конструктивные требования Для сборных элементов минимальные значения толщины защитного слоя бетона рабочей арматуры, указанные в таблице, уменьшают на 5 мм. Для конструктивной арматуры минимальные значения толщины защитного слоя бетона принимают на 5 мм меньше по сравнению с требуемыми для рабочей арматуры. Во всех случаях толщину защитного слоя бетона следует также принимать не менее диаметра арматуры и не менее 10 мм.. В изгибаемых, растянутых и внецентренно сжатых (при Ml/Nl > 0,3h) элементах, кроме фундаментов, толщина защитного слоя для растянутой рабочей арматуры, как правило, не должна превышать 50 мм. В защитном слое толщиной свыше 50 мм следует устанавливать конструктивную арматуру в виде сеток. Тема 9 Расчет элементов прямоугольного сечения с одиночной арматурой x – высота сжатой зоны бетона. Площадь сжатой части бетонного сечения: Ab b x; Плечо внутренней пары сил (расстояние от ц.т. сжатой зоны бетона до ц.т. растянутой арматуры): zb h0 0,5 x. Проверка прочности прямоугольного сечения с одиночной арматурой Уравнений равновесия у нас только два. Предполагаем 1-й случай разрушения, тогда Сумма проекций всех сил на ось X равна 0. Rs As b x Rb 0, x отсюда Rs As . Rb b Если x xR , то действительно имеем 1-й случай разрушения. Условия прочности : Сумма моментов относительно ц.т. растянутой арматуры: M 0; M M R b x h 0,5 x ; (1) s u b 0 либо Сумма моментов относительно центра сжатой зоны бетона: M 0; M M R A h 0,5 x ; b u s s 0 (2) Уравнение (1) будет иметь вид x x M M u Rb b x h0 0.5 x Rb b h 1 0.5 h0 h0 Rb b h02 1 0.5 Rb b h02 m , 2 0 x 0.5 x 1 где обозначено m 1 0.5 . h0 h0 Плечо внутренней силы zb выражаем через коэффициент . 0.5 x zb h0 0.5 x h0 1 h 0 1 h0 , h0 2 где zb . h0 Тогда уравнения равновесия примут вид: Rb b h0 Rs As ; M M u m Rb b h02 ; (1) или M M u Rs As h0 (2) Если x > xR - 2-й случай разрушения. Это значит сечение переармировано, т.е. напряжения в растянутой арматуре в момент разрушения изгибаемого элемента будут меньше её прочности, арматура будет недогружена M M u Rb b xR h0 0.5 xR Rb b h02 R . При M < Mu прочность сечения обеспечена. Порядок расчета на прочность прямоугольного сечения с одиночной арматурой Предполагаем, что у нас первый случай разрушения, т.е . 1. Находим величину сжатой зоны бетона из уравнения Rs As b x Rb 0, Rs As x , . Rb b h0 2. Сравниваем величину с величиной R, которую можно посчитать x по формуле СП 63, а можно взять из СП. Класс арматуры А240 А300 А400 А500 В500 R 0.612 0.577 0.531 0.493 0.502 R 0.425 0.411 0.390 0.372 0.376 M M u Rs As h0 0.5 x 2 должно выполняться условие M M R h h x 4. При u R b 0. R 0 При x R h0 несущая способность сечения (т.е. прочность) 3. При x R h0 должно выполняться условие не зависит от количества арматуры. Порядок подбора арматуры в прямоугольном сечении с одиночной арматурой M M u Rb b x h0 0.5 x . 2. Находим из этого квадратного уравнения высоту сжатой зоны x. 3. При x R h0 отсюда Rs As b x Rb 0; b x Rb Rb b h0 As . Rs Rs Или из суммы моментов относительно ц.т. сжатой зоны бетона As 4. При M Rs h0 0.5 x x R h0 M M . Rs h0 Rs h0 1 2 - (второй случай разрушения) никакое количество арматуры не обеспечит прочность сечения, потому что сечение будет разрушаться из-за разрушения сжатой зоны бетона, поэтому увеличиваем класс бетона или размеры сечения, или ставим арматуру в сжатой зоне. Порядок подбора арматуры прямоугольном сечении с одиночной арматурой по таблице 1. Вычисляем величину 2. Если m R M m . 2 Rb b h0 по таблице находим m 1 0.5 . 1 1 1 2 m , 1 . 2 тогда 3. Если As Rb b h0 M . Rs Rs h0 m R требуется увеличить размеры сечения, повысить класс бетона, установить сжатую арматуру (по отдельности или в любом сочетании). Расчет прочности изгибаемых элементов прямоугольного профиля с двойной арматурой Элементы с двойной арматурой – это элементы, в которых арматуру по расчету устанавливают и в растянутой и в сжатой зонах. Сжатую арматуру устанавливают: • когда прочность бетона недостаточна, т.е. бетона и размеров сечения невозможно; x R h0 , а увеличение класса • Когда эпюра изгибающих моментов двухзначна (неразрезные балки, ригели рам) или при знакопеременных нагрузах; • для уменьшения эксцентриситета от силы обжатия в предварительно напряженных элементах. Предполагаем первый случай разрушения. Высота сжатой зоны определяется из уравнения равновесия всех продольных сил: Rb b x Rsc As Rs As 0, где Rsc и Asc – расчетное сопротивление сжатию и площадь сечения арматуры, установленной в сжатой зоне, a’ – расстояние от сжатой грани сечения до оси, проходящей через центра тяжести сжатой арматуры. Отсюда высота сжатой зоны бетона Rs As Rsc As x . Rb b Rs As Rsc As . Rb b h0 Уравнение прочности в моментах относительно ц.т. растянутой арматуры при R - первый случай разрушения. Предельный момент равен M u Rb x b h0 0.5 x Rsc As h0 a Rb h02 b 1 Rsc As h0 a . 2 При R - второй случай разрушения В этом случае для бетонов класса не выше В30 и арматуры классов А400 и А500 применяются те же формулы прочности с заменой x на xR: Предельный момент равен M u Rb xR b h0 0.5 xR Rsc As h0 a . Особый случай разрушения изгибаемых элементов с двойной арматурой Если величина сжатой зоны x 2a’, то изменяется напряженное состояние в сечении В этом случае сжатая арматура оказывается расположенной вблизи нейтральной оси и сжатая зона не оказывает заметного влияние несущую способность сечения. В этом случае плечо внутренней пары z (расстояние между центрами тяжести сжатой зоны бетона и растянутой арматуры) практически равно плечу zs (расстояние между ц.т. растянутых и сжатых стержней). Условие равновесия имеет вид: M 0; M M R A z . u s s s При M < Mu прочность сечения обеспечена. Порядок расчета на прочность прямоугольного сечения с двойной арматурой 1. Из уравнения равновесия nN = 0 находим высоту сжатой зоны бетона: Rs As Rsc As x Rb b ,и x . h0 2. Сравниваем величину с величиной R. 3. При x R h0 должно выполняться условие: M Rb x b h0 0.5 x Rsc As h0 a . 4. При x R h 0 должно выполняться условие M R Rb h02 Rsc As h0 a . 5. При x 2 a должно выполняться условие: M M u Rs As zs . Порядок подбора арматуры прямоугольного сечения с двойной арматурой 1. Находим предельный момент, который может воспринять прямоугольное сечение с одиночной арматурой в растянутой зоне M umax Rb b xR h0 0.5 xR . 2. Найти максимальную одиночную арматуру, соответствующую этому моменту: As max b xR Rb . Rs 3. Найти величину изгибающий момент, который должна воспринимать сжатая арматура M M M umax . 4. Чтобы воспринять этот момент нужно поставить в сжатую зону дополнительную арматуру. Из условия равновесия моментов относительно растянутой арматуры M Rsc As zs ; As' As M . Rsc zs 5. Добавляем в растянутую зону столько же арматуры As Aamax As Aamax As' . Порядок подбора арматуры прямоугольного сечения с двойной арматурой по алгоритму нормам 1. Вычисляем величину 2. Если m R M m . 2 Rb b h0 находим 1 1 2 m . Сжатая арматура по расчету не требуется. Rb b h0 As . Rs 3. Если m R , 2 M R b h R b 0 As . Rs h0 a M As Rsc b h0 a . Уточняем m 2 Rb b h0 As R Rb b h0 Rs As . Расчет прочности изгибаемых элементов таврового сечения а) b'f h'f б) h' 2 b'f1 1 2 3 1 3 b в) AS AS b'f1 c г) b'f1 c Тавровые сечения: а - балка с полкой в сжатой зоне, б – то же в растянутой зоне, в – тавровое сечение в составе монолитного перекрытия, г – то же в составе сборного перекрытия, 1 – полка, 2 – сжатая зона, 3 - ребро. При большой ширине полок участки свесов, более удаленные от ребра включаются в работу меньше. Поэтому в расчет вводят эквивалентную ширину свесов полки: b f b 2 b f 1. Ширина свеса полки в каждую сторону от ребра принимается не более 1/6 пролета: а) при наличии поперечных ребер или при h f 0.1 h - не более 1/2 расстояния в свету между продольными ребрами; б) при отсутствии поперечных ребер или при расстояниях между ними больших, чем расстояния между продольными ребрами) и h f 0.1 h – не более 6 h f ; в) при консольных свесах полки: • при h f 0.1 h - не более 6 h f ; • при 0.05 h h f • при h f 0.1 h - не более 3 hf ; 0.05 h - свесы не учитываются. Расчетный случай 1. Нейтральная ось проходит в полке x hf h'f x h h -0.5x R s As b a a M h h x R b b'f x b'f As В этом случае расчет тавровых сечений не отличается от расчета прямоугольных сечений шириной b’f. Условие прочности как сумма всех моментов относительно ц.т. арматуры: M M u Rb b f x h0 0.5 x . Rb b f h02 m . Высота сжатой зоны определяется из суммы проекций всех сил на горизонтальную ось: Rb b f x Rs As 0. Откуда высота сжатой зоны будет равна Rs As x ; R b b Заменив x на f h0 , получим уравнение равновесия и относительную высоту сжатой зоны бетона в виде: R b h R A 0. b f 0 s s Rs As . R b h b f 0 Расчетный случай 2. Нейтральная ось пересекает ребро 0.5(b'f -b) 0.5(b'f -b) b h -0.5h'f M1 h h h h'f R b b'f x A s1 b'f Rs As . R b h R b b'f x 0 b x h -0.5x M2 a As a h x a f h'f b b R s A s1 a a b h h h x h'f b'f R s A s2 A s2 Вверху - расчетная схема для сжатых свесов полки; Внизу - расчетная схема для ребра. As As1 As 2 . As1 - как бы арматура свесов; As 2 - как бы арматура ребра. Условие прочности в виде суммы моментов относительно ц.т. растянутой арматуры: M M u M 1свесы M 2ребро Rb b f b h f h0 0.5 h f Rb b x h0 0.5 x . Высота сжатой зоны определяется из уравнения равновесия Nx 0 , при этом Nb,свесы Nb , ребра N s Rb b f b h f Rb b x Rs As Rb b f b h f Rb b h0 Rs As 0. Используя соотношение x h0 условие прочности сечения перепишем в виде: M M u Rb b f b h f h0 0.5 h f m Rb b h02 ; Определение положения нейтральной оси b'f h'f h x x R s As b a a h h M h -0.5h'f R b b'f x As Если изгибающий момент от расчетных нагрузок оказывается меньше внутреннего момента, воспринимаемого сжатой полкой таврового сечения, относительного центра тяжести растянутой арматуры или равен ему, то нейтральная ось проходит в полке, т.е. если M M uсвесов Rb b f h f h0 0.5 h f , то н.о. проходит в полке, т.е. x hf и расчёт ведётся как прямоугольного сечения. Если условие не выполняется, то нейтральная ось пересекает ребро. Если известна площадь растянутой арматуры As, то положение нейтральной оси необходимо определять из суммы проекций всех сил на продольную ось элемента N 0. x Полагается, что ось проходит по нижней грани полки: Rs As Rb b f h f . Если условие выполняется, нейтральная ось проходит в полке, если условие не выполняется, нейтральная ось проходит в ребре. Порядок расчета на прочность тавровых сечений: Rs As Rb b f h f . 1. Проверяем условие 2. Если условие выполняется, то граница сжатой зоны проходит в полке, и считаем как прямоугольное сечение шириной bf ’. 3. Если условие не выполняется, и граница сжатой зоны проходит в ребре, то определяем высоту сжатой зоны бетона по формуле: x 4. Если Rs As Rb b f b h f Rb b . x R h0 проверяем прочность сечения по условию: M M ult Rb b x h0 0.5 x Rb b f b h f h0 0.5 h f . 5. Если x R h0 принимаем x R h0 . Порядок подбора арматуры в тавровых сечениях 1. Предполагаем 1 случай разрушения (т.е. не учитываем сжатую арматуру). Находим положение н.о. M Rb b f h f h0 0.5 h f . 2. Если условие выполняется, то граница сжатой зоны проходит в полке, и подбор арматуры проводится как для прямоугольного сечения шириной bf’. 3. Если условие не выполняется, то определяем момент, воспринимаемый свесами полок (относительно растянутой арматуры): M свесы Rb b f b h f h0 0.5 h f . 4. Найдем продольную арматуру свесов, необходимую для восприятия момента (из суммы продольных сил) Asсвесы Rb b f b h f . Rs ребро M M свесы . 5. Найдем момент воспринимаемый ребром: M 7. Если m R находим M ребро m . 2 Rb b h0 As Asребро Asсвесы . 8. Если m R имеем второй случай разрушения и либо увеличиваем класс бетона или размеры сечения, либо устанавливаем сжатую арматуру. Порядок подбора арматуры в тавровых сечениях по СП (с двойной арматурой) 1. Площадь сжатой арматуры подбираем из условия (предполагая, что нейтральная ось проходит в ребре): A M R Rb b h02 Rb b f b h f h0 0.5 h f Rsc h0 a s 2. Проверяем условие . M Rb b f h f h0 0.5 h f Rsc As h0 a . 3. Если условие выполняется, то граница сжатой зоны проходит в полке, и подбор арматуры проводится как для прямоугольного сечения шириной bf ’. 4. Если условие не выполняется, то площадь растянутой арматуры определяется по формуле: As где m Rb b h0 1 1 2 m Rb b f b h f Rsc As Rs M Rb b f b h f h0 0.5 h f Rsc As h0 a Rb b h 2 0 . . Если m R , требуется увеличить размеры сечения, повысить класс бетона. Тема 10 Расчет прочности изгибаемых элементов по наклонным сечениям В приопорной зоне железобетонная балочная конструкция работает в условиях плоского напряженного состояния, при наличии нормальных и касательных напряжений, неупругих деформаций в арматуре и бетоне, наличие нормальных и наклонных трещин, влияния поперечных сил в продольной арматуре и сил зацепления, возникающих в наклонной трещине при ее подвижке. Разрушение происходит по одной из трех схем: а) Раздавливание тонкой стенки (ребра) по наклонной полосе между трещинами от действия главных сжимающих напряжений mc ; б) Взаимный сдвиг двух частей изгибаемого элемента, разделенных наклонной трещиной под действием поперечной силы Q; в) Взаимный поворот относительно точки О двух частей изгибаемого элемента, разделенных наклонной трещиной, который вызывается действием изгибающего момента М . Характер разрушения изгибаемого элемента по наклонному сечению: при действии сосредоточенных сил; при загружении конструкции равномерно распределенной нагрузкой 1 - критическая наклонная трещина, 2 – дополнительные наклонные трещины, 3 – продольная трещина, 4 – раздавленный участок сжатой зоны бетона, с – расстояние от внутренней грани опоры до вершины наклонной трещины. Условие образования наклонной трещины mc 2 mt 2 2 2 2 2 2 2 Максимальные значение главных растягивающих напряжений получим при = 0 b h2 Q 8 QS 3Q mt I b b h3 2bh b 12 Трещина возникает , когда главное растягивающее напряжение достигает величины Rbt, тогда условие прочности бетонного элемента по наклонному сечению запишется в виде 2 2 Q Qbmin Rbt b h 1.1 Rbt b h0 3 3 Условие по СП 63 Qbmin 0.5 Rbt b h0 1. Расчет на действие поперечной силы по наклонной полосе между трещинами Установлено, что предельная сила Q, воспринимаемая бетонной полосой, пропорциональна его ширине b и рабочей высоте сечения h0. Т.к. бетон в этом случае разрушается в основном от сжатия в расчетную формулу вводится прочность бетона на сжатие Rb. А т.к. полоса бетона между наклонными трещинами находится в условиях двухосного напряженного состояния (растяжение-сжатие), то прочность бетона в этом случае будет ниже, чем при одноосном напряженном состоянии. Условие прочности на действие поперечной силы расположенном не менее чем на расстоянии h0 от опоры: Q Qbc 0.3 Rb b h0 Q в нормальном сечении, 2. Расчет на действие поперечной силы по наклонной трещине Рассматривается система внешних и внутренних сил, приложенных к железобетонному блоку, отделенному наклонным сечением, проходящим по наклонной трещине. S S S S S S q Qb D q sw Rsw Asw q sw Q c q sw S S S c0 Условие прочности наклонного сечения по поперечной силе Поперечная сила Q в наклонном сечении Важное значение имеет точка приложения нагрузки, а также характер ее действия во времени. Если нагрузка приложена сверху от наклонной трещины Q Qmax Fi q c где Qmax – поперечная сила на опоре; F i – сосредоточенные силы в пределах блока; q – равномерно распределенная нагрузка в пределах блока . Если нагрузка является временной и может быть перемещена, а также если она приложена не по верхней грани элемента, а в пределах его высоты, ее разгружающее действие не учитывается или учитывается лишь ее часть. Поперечная сила Qs , воспринимаемая поперечной арматурой Стержни поперечной арматуры, пересекающие наклонную трещину, расположены дискретно и растянуты неодинаково. Однако при расчете усилия в них принимают равным расчетному сопротивлению поперечной арматуры, а указанные обстоятельства учитывают введением понижающего коэффициента условий работы арматуры в виде хомутов: Rsw Rs s1 Для хомутов (поперечных стержней) Qsw Rsw Asw Для отгибов (наклонных стержней) Qs,inc Rsw As,inc sin где - угол наклона стержней к продольной оси элемента. Для удобства расчетов равнодействующие силы в хомутах заменяем распределенными: Qsw Rsw Asw c0 qsw c0 . ssw В нормах при определении усилия в поперечной арматуры введен понижающий коэффициент запаса φsw =0,75: Qsw 0.75 qsw c0 Поперечная сила Qb, воспринимаемая бетоном Поперечная сила, воспринимаемая бетоном, зависит от размеров сечения (b и h), прочности бетона на растяжение Rbt, а также от так называемого относительного пролета среза (с/h0). C увеличением этой величины происходит резкое падение Qb приблизительно по гиперболической зависимости 1.5 Rbt b h0 1.5 Rbt b h02 M b Qb c c c h0 По результатам экспериментов установлено, что при малых и больших значениях относительного пролета среза значение Qb сохраняет значения близкие к постоянным. По нормам поперечная сила, воспринимаемая бетоном, принята не более Qbmax 2.5 Rbt b h0 и не менее Qbmin 0.5 Rbt b h0 Влияние продольной силы на несущую способность При сжатии несущая способность сечения по поперечной силе увеличивается, а при растяжении - наоборот, снижается. Влияние сжимающих и растягивающих напряжений при расчете по полосе между наклонными сечениями и по наклонным сечениям согласно СП 63.1330.2018 учитывается с помощью коэффициента φn. при 0 σcp 0.25∙Rb; при 0.25∙Rb σср 0.75∙Rb; 1.25 при 0.75∙Rb σср Rb; при 0 σt 2Rbt где σср, σt - среднее сжимающее и среднее растягивающее напряжение в бетоне от воздействия продольных сил, принимаемое положительным. Расчетная длина проекции опасного наклонного сечения и проекция наклонной трещины А. Действие распределенной нагрузки Случай 1 Случай 2 В случае 1 длина наклонной трещины с0 совпадает с пролетом среза с. Найдем величину пролета среза, при которой несущая способность отсеченного трещиной элемента минимальна: d d d 1.5 Rbt b h02 Q (Qb Qsw ) [( ) 0.75 qsw c] 0 dc dc dc c 1.5 Rbt b h02 Mb c0 c . 0,75 qsw 0,75 qsw В случае 2 начало и вершина опасной трещины неизвестны. В этом случае СП даёт формулу c Mb , q Расчётная величина проекция наклонной трещины может оказаться очень маленькой или очень большой, чего не наблюдается в экспериментах. Поэтому на основе эмпирических данных значение c ограничено: не больше 2h0 и не меньше h0. Граница между двумя случаями По СП 63 при действии равномерно распределенной нагрузки q пролёт среза C принимается равным: в случае если Mb 2 h0 q1 1 0.5 qsw Rbt b то c или qsw 2 Rbt b Mb . 0.75 qsw q1 В противном случае проекция опасного сечения принимается равной c Значение нагрузки q1 распределенная нагрузка. Mb q1 принимается равным q, если действует сплошная Так как нагрузка часто бывает приложена не равномерно, а сосредоточена в отдельных местах, то можно вычислить с по формуле (приняв q=0): c Mb 0.75 qsw Б. Действие сосредоточенной силы при Случай 1 Случай 2 при a 2h0 при a 2 h0 c0 c h0 c0 c 2 h0 Mb c 0.75 qsw Mb c 0.75 qsw Mb с c0 0.75 qsw при но не меньше h0 Mb c c0 0.75 q sw но не больше 2h0 Конструктивные требования • В опасных зонах при равномерно распределенной нагрузке в ¼ пролета шаг хомутов устанавливается не более h0/2 и не более 300 мм; • Если поперечная сила по расчету воспринимается только бетоном, то сплошных плитах, а также в многопустотных и часторебристых плитах высотой менее 300 мм и в балках (ребрах) высотой менее 150 мм на участках элемента, поперечную арматуру можно не устанавливать. • Если поперечная сила по расчету воспринимается только бетоном, то при высоте балок и ребер плит более 150 мм и часторебристых плитах высотой более 300 мм шаг хомутов не более ¾ h0 и не более 500 мм. • Диаметр поперечной арматуры в вязаных каркасах изгибаемых элементов принимают не менее 6 мм. • В сварных каркасах диаметр поперечной арматуры принимают не менее диаметра, устанавливаемого из условия сварки с наибольшим диаметром продольной арматуры. Максимальный шаг хомутов В расчетах необходимо учитывать, что опасная наклонная трещина может образоваться между двумя соседними хомутами, тогда она должна восприниматься только бетоном. Из условия Q Qb можно определить максимально расстояние между хомутами: допустимое 1.5 Rbt b h02 Q Qb c В СП 63 с запасом (коэффициент 1,5 не учитывается) Rbt b h02 c S max Q Поперечная арматура учитывается в расчете, если выполняется условие: qsw 0.25 Rbt b Порядок расчета на прочность по наклонным сечениям Rsw Asw , при этом S должно быть меньше Smax S 2. Проверяем условие qsw 0.25 Rbt b , Если условие не выполняется, то хомуты не qsw 1. Определяем величину учитываются и элемент рассчитывается как балка без арматуры. 2 3. Определяем момент, воспринимаемый бетоном сжатой зоны M b 1.5 Rbt b h0 4. Определяем величину проекции опасного наклонного сечения: а. При действии сосредоточенных сил определяем величину пролета Mb среза, расстояние от опоры до точки приложения силы, не больше 2h0 c 0.75 qsw и не менее h0; б. При действии сплошной равномерно распределенной Mb c нагрузки q Но если Mb 2 h0 Mb qsw или 2 c , то не больше 2 h0 и не менее h0; q1 1 0.5 qsw Rbt b q 0.75 qsw Rbt b 5. Принимаем величину проекции наклонной трещины с= с0 но не меньше h0 и не больше 2h0 . 6. Определяем величины и Qsw 0.75 qsw c 7. Проверяем условие: Q Qb Qsw , если условие выполняется – прочность обеспечена. Порядок подбора поперечной арматуры при действии равномерно распределенной нагрузки 1. Проверяем необходимость установки поперечной арматуры из условия: Q Qbmin 0.5 Rbt b h0 2. Проверяем условие прочности по бетонной полосе между наклонными сечениями: Q 0.3 Rb b h0 3. Вычисляем величину Qb1 2 M b q1 2 1.5 Rbt b h02 q1 тогда Q 2 Qb21 qsw 3 Mb если Qb1 2 Mb Q h0 тогда qsw если Qb1 Rbt b h0 тогда если 2 Mb Qb1 Q h0 Q Qb1 1.5 h0 qsw Q 0.5 b h0 3 h0 q1 1.5 h0 4. Проверяем условие min qsw qsw 0.25 Rbt b Если оно не выполняется, то пересчитываем требуемую поперечную арматуру по формуле: Q 8 q1 h qsw 0 1.5 2 Q 8 q 1 h Q 2 0 , 1.5 1.5 h 0 5. Задаемся шагом хомутов требованиям и по формуле: но не менее Q 3 q1 h0 3.5 S. Проверяем шаг хомутов: 1) по конструктивным Rbt b h02 Smax Q 6. Определяем требуемую площадь хомутов: Asw qsw S Rsw Порядок подбора поперечной арматуры при действии сосредоточенных сил 1. Проверяем необходимость установки поперечной арматуры из условия: Q Qbmin 0.5 Rbt b h0 2. Проверяем условие прочности по бетонной полосе между наклонными сечениями: Q 0.3 Rb b h0 3. Задаемся начальной величиной поперечного армирования. Для этого вычисляем величину: ci (но не более 3, принимая с равным расстоянию от опоры до точки h0 приложения i-ой силы). i грi Qi 1.5 грi 0.1875 0 принимаем qsw 0.25 Rbt b При i Rbt b h0 qsw Rbt b При i грi где 0 - меньшее из значений и 2. принимаем i 1.5 0.75 0 4. Проверяем прочность по поперечной силе и конструктивные требования, как указано выше. 3. Расчет железобетонных элементов по наклонным сечениям на действие моментов Условие прочности наклонных сечений на действие изгибающего момента Сумма моментов определяется относительно центра сжатой зоны бетона. Условие прочности: M M s M sw M – момент в наклонном сечении с длиной проекции c на продольную ось элемента от всех внешних сил, расположенных по одну сторону от рассматриваемого наклонного сечения; Ms – момент, воспринимаемый продольной арматурой, пересекающей наклонное сечение; Msw – момент воспринимаемый поперечной арматурой, пересекающей наклонное сечение. M s N s zs Ns – усилие в продольной растянутой арматуре, при отсутствии анкеров в пределах зоны анкеровки (т.е. если анкеровка не обеспечена) принимаемое равным: l N s Rs As s . lan ls – расстояние от конца арматуры до точки пересечения с ней наклонного сечения; lan – длина зоны анкеровки Плечо внутренней пары сил zs определяется по формуле: z s h0 0.5 x h0 Ns 2 Rb b Можно определять zs по упрощенной формуле: zs 0.9 h0 . M sw 0.5 qsw c 2 . Определение проекции расчетного сечения 1. При расчете прочности на М наклонное сечение и наклонную трещину не разделяют, а пользуются единой проекцией с. 2. Имеется ограничение: с 2ho. 3. Расчетное сечение определяется из условия минимума несущей способности по изгибающему моменту d M u M 0 dc а) Так как Ms = Ns zs = const, при действии равномерно распределенной нагрузки: c Qmax 2h0 qsw q б) При действии сосредоточенной силы значение c принимается наименьшему из двух величин: - или расстояния от опоры до точки приложения сосредоточенных сил - или c Qmax . qsw Длина зоны анкеровки Из условия минимума несущей способности по изгибающему моменту в наклонном сечении: w при этом, если Q h0 2 qsw Q 5 d s 15 d s 2 qsw q h w 2 h0 1 sw 0 5 d s 15 d s Q Тема 11 Расчет внецентренно сжатых элементов Два случая расчета бетонных элементов сжимающая сила лежит в пределах сечения бетонного элемента сжимающая сила лежит за пределами сечения бетонного элемента Для прямоугольного сечения: N Rb Ab 2 e0 Ab b h 1 h N Rbt b h 6 e0 1 h Два случая расчета железобетонных элементов Случай больших эксцентриситетов R Случай малых эксцентриситетов R Расчет на внецентренное сжатие: В плоскости действия момента: • Для статически неопределимых конструкций e =max( e0 ; ea) • Для статически определимых конструкций. e = ( e0 + ea) Из плоскости действия момента: e = ea Случайный эксцентриситет ea Наибольшая из 3-х величин: • 1/600 длины элемента Из-за искривления конструкции 1/30 высоты сечения; 10 мм. Из-за неточности монтажа Эксцентриситет от внешней нагрузки e0 Из-за неоднородности структуры. M N Гибкий внецентренно сжатый элемент под влиянием момента прогибается, поэтому значение начального эксцентриситета приложения нагрузки увеличивается. Это приводит в свою очередь к увеличению момента, и разрушение происходит при меньшей продольной силе по сравнению с негибким элементом. При гибкости элемента: lo/i > 14 для прямоугольных сечений - при lo/h > 4 влияние прогиба учитывается путем умножения момента (или расчетного эксцентриситета) на коэффициенты: M M M h h M t M - момент от вертикальных нагрузок, не вызывающих заметных горизонтальных смещений концов; Mh - момент от нагрузок, вызывающих заметных горизонтальное смещение концов (ветровых и т.п.); Mt - момент от вынужденных горизонтальных смещений концов (т.е. смещений, не зависящих от жесткости элемента, например температурных деформаций перекрытий); Значение коэффициента равно: 1 1 N N cr где Ncr - условная критическая сила (наибольшее значение сжимающей силы, при которой сжатое упругое тело (длинный стержень, тонкая пластина и т. п.) сохраняет начальную (неизогнутую) форму равновесия) . По формуле Эйлера: 2 D N cr 2 l0 l0 для коэффициента , а также при расчете на действие продольной силы со случайным эксцентриситетом Условие опирания Величина l0 С шарнирным опиранием по концам 1.0 l Шарнир на одном конце и жесткая заделка на другом конце 0.7 l Шарнир на одном конце и податливая заделка на другом конце 0.9 l С жесткой заделкой на двух концах 0.5 l С податливой заделкой на двух концах 0.8 l С жесткой заделкой на одном конце и податливой заделкой на другом 0.7 l для коэффициента h Условие опирания Величина l0 Шарнир на одном конце и жесткая заделка на другом конце 1.5 l Шарнир на одном конце и податливая заделка на другом конце 2.0 l С жесткой заделкой на двух концах 0.8 l С податливой заделкой на двух концах 1.2 l С жесткой заделкой на одном конце и податливой заделкой на другом 1.0 l D – жесткость железобетонного элемента в предельной стадии. D K b Eb I K s E s I s Kb и Ks – коэффициенты, определяемые по СП 63 Для произвольного сечения жёсткость равна : D 0.15 Eb I 0.7 Es I s . l 0.3 e Для прямоугольного сечения жесткость равна: 2 h a ' 0.0125 3 0 D Eb b h 0.175 . l 0.3 e h I и Is – момент инерции бетонного сечения и сечения всей арматуры относительно центра тяжести бетонного сечения; l – коэффициент, учитывающий влияние длительного действия нагрузки на прогиб элемента; e – коэффициент, принимаемый равным e0/h , но не менее 0.15; As A 's Es . bh Eb Расчет ЖБК по нормальным сечениям. Проверка прочности N Составляем уравнение равновесия как сумму всех сил nN=0 N Rs As Rsc As Rb b x 0 Отсюда находим высоту сжатой зоны бетона x N Rs As Rsc As Rb b Возможно два случая разрушения Если х хR составляем уравнение Ms= 0, то условие прочности x N e Rsc As h0 a x Rb b h0 2 Если условие выполняется прочность обеспечена. Если х > хR составляем уравнение Ms= 0, в котором sc для мягких сталей и бетонов класса не выше В30 определяется из совместного решения уравнений: Rb b x N s As Rsc As 1 Rs 2 1 s 1 R Проверка прочности сечений с симметричным армированием Проверку прочности прямоугольных сечений с симметричной арматурой (RsAs= RsA’s) проводят из условия равенства нулю суммы моментов относительно центра тяжести растянутой арматуры Ms = 0: N M Rb b x h0 0.5 x Rsc A's h0 a' 2 Высота сжатой зоны x находится из условия равенства 0 суммы всех продольных сил. N s Rb b x 0 тогда x N , Rbb n x . h0 Если принимаем x n h0 Если принимаем n 1 R 2 s R 1 R 2 s R определяется как для изгибаемого элемента. s Rs As Rb b h0 Порядок подбора арматуры по СП 63 в сечениях с симметричным армированием 1. Предполагаем первый случай разрушения. 2. Составляем уравнение равновесия nN = 0. 3. Определяем величину При ξn R n As As ' N Rb b h0 Rb b h0 Rs m1 n 1 n 1 2 5. При ξn > R тогда Следовательно в уравнениях равновесия действует s вместо Rs m1 1 R b h0 2 . As As ' b Rsc 1 где n 1 R 2 s R 1 R 2 s s m1 1 1 1 2 1 h a' M N 0 2 m1 2 Rb b h0 1 n R 2 a' h0 1 Расчет внецентренно сжатых элементов с жесткой арматурой Предпосылки расчета прочности элементов с жесткой арматурой: • Рабочая высота сечения принимается равной расстоянию от наиболее сжатой грани сечения до общего центра тяжести жесткой и гибкой растянутой арматуры; • При расчете внецентренно сжатых элементов с жесткой арматурой площадь сечения сжатой зоны принимают за вычетом площади, занятой арматурой, что равносильно снижению расчетного сопротивления жесткой арматуры этой зоны до значения (Rsr - Rb). При учете влияния продольного изгиба жесткость элемента определяется по формуле: D 0.15 Eb I 0.7 Es I s sr I sr l 0.3 e sr E sr Eb Isr – момент инерции жесткой арматуры. Условие прочности элементов с жесткой арматурой (Ms = 0): e1 – эксцентриситет приложения продольного усилия относительно равнодействующей усилий в растянутой жесткой и гибкой арматуре; a’r – расстояние до ц.т. сжатой жесткой арматуры до сжатой грани сечения. Случай 1 – x xR: x N Rs As Rsc As Rsr Rb Asr,c Rsr Asr,t Rb b e1 – эксцентриситет приложения продольного усилия относительно равнодействующей усилий в растянутой жесткой и гибкой арматуре; a’r – расстояние до ц.т. сжатой жесткой арматуры до сжатой грани сечения. Случай 2 – x > xR N Rsc As Rsr Rb Asr ,c 1 R Rsr Asr Rs As 1 R x Rb b h0 1 R 2 Rsr Asr Rs As Для сечений, армированных высоким симметричным профилем: x N Rsc As 2 Rsr t r Rsr Asr,t Rs As Rb b 2 Rsr t где r – расстояние от сжатой грани бетона до центра тяжести жесткой арматуры; t – толщина стенки профиля жесткой арматуры или сумма толщин стенок нескольких профилей. Учет косвенного армирования Местное сжатие – это приложение нагрузки не по всей площади поперечного сечения, а только по ее части, что более опасно, так как вызывает высокую концентрацию напряжений в бетоне, приводит к образованию местных трещин и преждевременному разрушению Центрально сжатые элементы, усиленные косвенным армитрованием: а – спиралями или сварными кольцами, б – поперечными сварными сетками, в – то же под центрирующей прокладкой Расчет на местное сжатие Условие прочности: N Rb ,loc Ab ,loc . N – местная сжимающая сила; Rb,loc расчетное сопротивление бетона смятию; Аloc1 площадь смятия (площадь приложения сжимающей силы); коэффициент, зависящий от равномерности приложения силы N по площади смятия и учитывающий, по существу, полноту эпюры давления: Rb ,loc Rb b 1.0 b 0.8 Ab ,max Ab ,loc 2.5. 1 – элемент, 2 – площадь смятия, 3 – максимальная расчетная площадь, 4 – ц.т. площадей Ab,loc и Ab,max 5 - минимальная зона армирования сетками, при которой косвенное армирование учитывается в расчете При наличии косвенной арматуры в виде сварных сеток вместо Rb,loc в условие прочности подставляется Rbs,loc - расчетное сопротивление бетона сжатию, приведенное с учетом косвенной арматуры: Rbs,loc Rb,loc 2 s, xy Rs, xy s, xy 2 Rb,loc s , xy - коэффициент, определяемый по формуле s , xy A b ,loc,ef A b ,loc Ab,loc,ef – площадь, заключенная внутри контура сеток косвенного армирования (считая по их крайним стержням), но не превышающая Ab,max. Rs,xy – расчетное сопротивление растяжению косвенной арматуры; xy – коэффициент косвенного армирования: xy nx Asx l x n y Asy l y Ab,loc ,ef s nx, Asx, lx – число стежней, площадь сечения и длина стержня, считая в осях крайних стержней, в направлении x; ny, Asy, ly – то же в направлении y; s – шаг сеток косвенного армирования. Расчет условно центрально сжатых элементов N Rb Ab Rsc As,tot φ = φb + 2(φsb - φb)αs, но не более φsb где Аb – площадь сечения колонны; As,tot – площадь всей продольной арматуры в сечении колонны; φsb и φb - коэффициенты, принимаемые по таблицам 3.5 и 3.6 СП 52-101-2003 в зависимости от гибкости l0/h элемента, Коэффициент φb при l0/h 0 0,5 1,0 6 8 10 12 14 16 18 20 0,93 0,92 0,92 0,92 0,91 0,91 0,91 0,90 0,89 0,90 0,89 0,87 0,89 0,86 0,83 0,88 0,82 0,76 0,86 0,77 0,68 0,84 0,71 0,60 16 18 20 Коэффициент φsb при l0/h 6 8 10 12 14 А. При и при отсутствии промежуточных стержней (см. эскиз) или площади сечения этих стержней менее Аs,tot/3 0 0,93 0,92 0,91 0,90 0,89 0,88 0,86 0,83 0,5 0,92 0,91 0,91 0,90 0,88 0,87 0,83 0,79 1,0 0,92 0,91 0,90 0,90 0,88 0,85 0,80 0,74 Б. При или при площади промежуточных стержней (см. эскиз), равной или более Аs,tot/3 независимо от а 0 0,92 0,92 0,91 0,89 0,87 0,85 0,82 0,79 0,5 0,92 0,91 0,90 0,88 0,85 0,81 0,76 0,71 1,0 0,92 0,91 0,89 0,87 0,83 0,77 0,70 0,62 Обозначения, принятые в табл. 3.5 и 3.6: Nl - продольная сила от действия постоянных и длительных нагрузок. N - продольная сила от всех нагрузок. Требуемая площадь арматуры N As ,tot Rb Ab Rsc Расчет центрально и внецентренно растянутых элементов Условие прочности при центральном растяжении N Rs As где As- площадь сечения всей продольной арматуры. Бетон в расчётной модели отсутствует, т.к. в стадии 3 напряжённо-деформированного состояния сечение рассечено трещиной. Внецентренное растяжение Случай 1 Случай 2 Условие прочности Случай 1 Случай 2 N e Rs As h0 a N e Rsc As h0 a As As' N e' Rs ho a' N e Rs ho a' Rs As Rsc As' N x Rb b При х < 0 переходим с случаю 1 Если x < 2∙a, то сжатую арматуру в расчете не учитывают Если х ≤ ξRho N e Rsc As h0 a Rb b x h0 0.5 x Если х > ξRho в условие прочности подставляют х = ξR h o Тема 12 Расчет по второй группе предельных состояний Расчет по образованию и раскрытию трещин Расчеты по предельным состояниям второй группы включают: - расчет по образованию трещин; - расчет по раскрытию трещин; - расчет по деформациям (прогибам). Непродолжительное раскрытие трещин определяют от совместного действия постоянных и временных нагрузок. Продолжительное раскрытие – только от постоянных и временных длительных нагрузок. Расчет по деформациям следует производить на действие: постоянных, временных длительных и кратковременных нагрузок (при ограничении деформаций технологическими или конструктивными требованиями); постоянных и временных длительных нагрузок (при ограничении деформаций эстетическими требованиями. Трещины в железобетонных балках В процессе образования трещин различают три этапа: • возникновение микро трещин, когда они могут быть еще невидимыми, • раскрытие трещин, когда они становятся видимыми невооруженным глазом (ширина 0,02-0,03 мм), • раскрытие трещин до предельно возможной величины. Предельно допустимая ширина раскрытия трещин Условие Раскрытие трещин Класс арматуры acrc, ult, мм А240...А600, В500 0.4 А800, А1000, 1200- 1400, а также классов К1400, К1450, К1500, К1550, К1650 диаметром 12 мм и более 0,3 в 1500, 1600, а также классов К1500, К1550, К1650, К1750, К1850, К1900 диаметром менее 12 мм 0,2 А240...А600, В500 0.3 А800, А1000, 1200- 1400, а также классов К1400, К1450, К1500, К1550, К1650 диаметром 12 мм и более 0,2 в 1500, 1600, а также классов К1500, К1550, К1650, К1750, К1850, К1900 диаметром менее 12 мм 0,1 Непродолжительное Все 0.3 Продолжительное Все 0.2 Непродолжительное Обеспечение сохранности арматуры Продолжительное Ограничение проницаемости конструкций Основные положения норм при расчётах по 2-й группе предельных состояний 1. Cечения после деформирования остаются плоскими; 2. Эпюру напряжений в сжатой зоне бетона принимают треугольной формы, как для упругого тела; 3. Эпюру напряжений в растянутой зоне бетона принимают трапециевидной формы с напряжениями, не превышающими расчетных значений сопротивления бетона растяжению Rbt,ser; 4. Относительную деформацию крайнего растянутого волокна бетона принимают равной ее предельному значению εbt,ult: при кратковременном действии нагрузки εbt,ult = εbt2 принимают по таблице 6.10 СП 63.13330.2018 (в зависимости от величины относительной влажности окружающей среды); при двухзначной эпюре деформаций в сечении элемента εbt,ult = 0.00015. 5. Напряжения в арматуре принимают в зависимости от относительных деформаций как для упругого тела. Расчет по образованию трещин Расчет элементов по образованию трещин без предварительного напряжения В основе расчета лежит первая стадия работы конструкций (стадия до образования трещин) M M crc M crc Rbt , serW pl I Wpl 1.3 Wred 1.3 red yt где Ired – момент инерции приведенного поперечного сечения относительно его центра тяжести; I red I b I s I s' I, Is, I's – моменты инерции сечений соответственно бетона, растянутой и сжатой арматуры; yt – расстояние от наиболее растянутого волокна бетона до центра тяжести приведенного поперечного сечения элемента yt St ,red Ared Ared – площадь приведенного поперечного сечения элемента, определяемая по формуле Ared Ab As As' – коэффициент приведения арматуры к бетону по деформативности: Es Eb здесь St,red – статический момент площади приведенного поперечного сечения элемента относительно наиболее растянутого волокна бетона. При внецентренном сжатии или растяжении Моменты продольных сил N от внешней нагрузки принимают относительно ядровых точек при внецентренном сжатии M p N e0 r при внецентренном растяжении M p N e0 r Отличительной особенностью ядровой точки является то, что приложенная в ней продольная сила вызывает на противоположной грани сечения нулевые напряжения. M crc Rbt , serWpl Nex ex – расстояние от точки приложения продольной силы N (расположенной в центре тяжести приведенного сечения элемента) до ядровой точки, наиболее удаленной от растянутой зоны, трещинообразование которой проверяется. ex Wpl Ared В формуле знак «плюс» принимают при сжимающей продольной силе N, «минус» при растягивающей силе. При центральном растяжении Усилие Ncrc при образовании трещин : N crc Ared Rbt ,ser Этапы трещинообразования в преднапряженных конструкциях M crc M p M bt Мр момент, который погашает предварительное обжатие крайнего волокна бетона, т.е. уменьшает в нем сжимающие напряжения от bp до 0 Мbt момента, который повышает в этом же волокне растягивающие напряжения от 0 до сопротивления бетона растяжению Rbt,ser. M p Wred pb Из уравнения моментов относительно ц.т. сечения: bp P eop P Ared Wred P eop P P r eop M p Wred Ared Wred r Wred Ared - расстояние от центра тяжести приведенного сечения до верхней ядровой точки M bt W pl Rbt ,ser Wpl упруго-пластический момент сопротивления приведенного сечения. Расчет преднапряженных элементов. Момент образования трещин предварительно напряженных изгибаемых элементов c учетjv неупругих деформаций растянутого бетона определяют как для сплошного упругого тела по формуле: M crc Rbt , ser W pl P eя р где W - момент сопротивления приведенного сечения для крайнего растянутого волокна; eя р = е0р + r - расстояние от точки приложения усилия предварительного обжатия Р до ядровой точки, наиболее удаленной от растянутой зоны, трещинообразование которой проверяется; е0 р - то же, до центра тяжести приведенного сечения; r - расстояние от центра тяжести приведенного сечения до ядровой точки. - коэффициент, учитывающий влияние неупругих деформаций растянутой зоны на сопротивление сечения В формуле знак « + » принимают, когда направления вращения моментов Р еяр и внешнего изгибающего момента М противоположны; « - » - когда направления совпадают. Момент сопротивления W и расстояние от центра тяжести приведенного поперечного сечения до ядровой точки r определяют по формулам: W I red yt Wred r Ared где Ired - момент инерции приведенного поперечного сечения относительно его центра тяжести; Ared - площадь приведенного поперечного сечения элемента; α - коэффициент приведения арматуры к бетону; yt - расстояние от наиболее растянутого волокна бетона до центра тяжести приведенного поперечного сечения элемента. Допускается момент сопротивления W определять без учета арматуры. В этом случае значения Is, I's, As, A's в формулах принимают равными нулю. Усилие Ncrc при образовании трещин в центрально растянутых элементах определяют по формуле: N crc Ared Rbt , ser Трещиностойкость в стадии обжатия, транспортировки и монтажа: Сила обжатия Р1 (с учетом первых потерь) создает момент того же знака, поэтому ее рассматривают как внешнюю силу, которая растягивает верхнюю грань. M w P1 eop r Rbt , ser Wpl где Wpl упруго-пластический момент сопротивления для верхней грани. Величина Rbt,ser должна соответствовать передаточной прочности бетона. Тема 13 Расчет по раскрытию трещин Ширина раскрытия трещин представляет собой разность удлинения арматуры и растянутого бетона на участке между трещинами, но средней деформацией растянутого бетона обычно пренебрегают, т.к. она существенно меньше, чем деформации растянутой арматуры: a crc sm ls btm ls sm ls Основное расчетное условие: a crc a crc , ult Ширину раскрытия трещин acrc определяют, исходя из взаимных смещений растянутой арматуры и бетона по обе стороны трещины на уровне оси арматуры, и принимают: • при продолжительном раскрытии: a crc a crc ,1 acrc acrc ,1 acrc acrc ,1 (acrc ,2 acrc ,3 ) • при непродолжительном раскрытии: Ftot – полная нагрузка; Fl – постоянная и длительная нагрузка; Fcrc – нагрузка в момент образования трещин. Кратковременная нагрузка: Fsh = Ftot Fl ширина раскрытия трещин от продолжительного действия постоянных и длительных нагрузок (точка 2 на рисунке). Определяется при M = Ml и коэффициенте l = 1.4 acrc,2 - ширина раскрытия трещин от непродолжительного действия всех нагрузок: постоянных, длительных и кратковременных нагрузок, т.е. от полной нагрузки (точка 3 на рисунке). Определяется при M = Mtot и при l = 1.0. acrc,3 - ширина раскрытия трещин от непродолжительного действия постоянных и временных длительных нагрузок (точка 4). Определяется при M=Ml и коэффициенте acrc,1 l = 1.0. Разность Δ acrc = acrc,2 - acrc,3, т.е. расстояние между точками 3 и 4 – это приращение ширины непродолжительного раскрытия трещин при действии кратковременной нагрузки. В основу расчета положена вторая стадия напряженно-деформированного состояния. acrc 1 2 3 s где s Es ls 1 – коэффициент, учитывающий продолжительность действия нагрузки и принимаемый равным: 1.0 – при непродолжительном действии нагрузки; 1.4 – при продолжительном действии нагрузки. 2 – коэффициент, учитывающий профиль арматуры и принимаемый равным: 0.5 – для арматуры периодического профиля и канатной; 0.8 – для гладкой арматуры (класса А240). 3 – коэффициент, учитывающий характер нагружения и принимаемый равным: 1 – для изгибаемых и внецентренно сжатых элементов; 1.2 – растянутых элементов. s – приращение напряжений в продольной арматуре (растянутой или предварительно напряженной) от внешней нагрузки. Его определяют из суммы моментов относительно точки приложения равнодействующей усилий в сжатой зоне. Для изгибаемых элементов прямоугольного, двутаврового и таврового сечения без предварительного напряжения: M s zs As Плечо внутренней пары находят по формуле zs h0 Согласно СП 63.13330.2018 для элементов прямоугольного, таврового (с полкой в сжатой зоне) и двутаврового поперечного сечения допускается значение zs принимать равным 0.8h0 . Для преднапряженных изгибаемых (или внецентренно сжатых) элементов прямоугольного, двутаврового и таврового сечения : Ms P z s , Asp As но не более Rs , ser sp , M s M P esp . z – плечо внутренней пары сил, равное z = h0, где определяется по таблице СП :63. Согласно СП 63.13330.2018 для элементов прямоугольного, таврового (с полкой в сжатой зоне) и двутаврового поперечного сечения допускается значение z принимать равным 0.7h0. На ширину раскрытия трещин большое влияние оказывают характеристики арматуры и предельная растяжимость бетона, силы сцепления арматуры и бетона на участке между трещинами. à 3 – коэффициент, учитывающий неравномерное распределение относительных деформаций растянутой арматуры между трещинами. 2 1 àcrc s Ì lcrc àcrc s s(x) s á без предварительного напряжения: õ s = 1, bt â bt(x) õ в предварительно напряженных конструкциях: если a crc a crc , ult s 1 0.8 s,crc s s,crc – приращение напряжений в растянутой арматуре в сечении с трещиной сразу после образования нормальных трещин. Определяется так же как и s, но при значении M = Mcrc. при s,crc > s s = 0.2 ls – базовое расстояние между трещинами. Находится из условия, что разность усилий в растянутой арматуре в двух соседних сечениях с трещиной уравновешивается усилием сцепления арматуры с бетоном на участке между трещинами: s1 s 2 As S lcrc - коэффициент полноты эпюры сцепления, - максимальное напряжение сцепления бетона с арматурой, S = ds – периметр арматурного стержня. без предварительного напряжения: в предварительно напряженных конструкциях: A 10 d s ls 0.5 bt d s 40 d s или 400 мм As 10 d s l s 0.5 Abt d s 40 d s или 400 мм As Asp Abt – площадь сечения растянутого бетона, определяемая в общем случае с использова- нием двухлинейной диаграммы деформирования бетона, но не менее площади при высоте 2a и не более площади при высоте 0.5h. Определяется в зависимости от высоты растянутой зоны y. . Для прямоугольного, таврового и двутаврового сечений: y yt k yt – высота растянутой зоны бетона, определяемая как для упругого материала при коэффициенте приведения арматуры к бетону S yt red Ared yt S red Ared P Rbt ,ser k – поправочный коэффициент, равный: •0.9 – для прямоугольных и тавровых сечений с полкой в сжатой зоне; •0.95 – для двутавровых и коробчатых сечений, а также тавровых с полкой в растянутой зоне Что лучше: увеличивать количество стержней или их диаметр? Почему с увеличением диаметра раскрытия трещин в конструкциях? арматуры увеличивается ширина При увеличении диаметра арматуры в 2 раза площадь сечения увеличивается в 22 = 4 раза, усилие в ней также возрастает в 4 раза, а периметр увеличивается только в 2 раза. Таким образом, увеличение контакта арматуры с бетоном отстаёт от роста усилия, поэтому при одинаковых напряжениях в арматуре с увеличением диаметра ухудшается сцепление и возрастает раскрытие трещин. Расчет по раскрытию трещин внецентренно сжатых и центрально и внецентренно растянутых элементов для внецентренно растянутых элементов при приложении силы N между центрами тяжести арматуры s N e' A s h 0 a ' для центрально растянутых элементов s N As для внецентренно сжатых элементов прямоугольного сечения s Ne crc As h 0 crc - коэффициент, определяемый по нормам Тема 14 Расчет изгибаемых элементов по деформациям Расчет по деформациям следует производить на действие: постоянных, временных длительных и кратковременных нагрузок при ограничении деформаций технологическими или конструктивными требованиями. постоянных и временных длительных нагрузок при ограничении деформаций эстетико-психологическими требованиями. (1/r)1 – кривизна от непродолжительного действия всех нагрузок (постоянной, длительной и кратковременной); (1/r)2 – кривизна от непродолжительного действия постоянных и длительных нагрузок; (1/r)3 – кривизна от продолжительного действия постоянных и длительных нагрузок; (1/r)4 – кривизна от выгиба элемента вследствие усадки и ползучести бетона от усилия предварительного обжатия Определение кривизны железобетонных элементов 1. В элементах без предварительного напряжения полную кривизну определяют по формуле: - для участков без трещин в растянутой зоне 1 1 1 . r r 1 r 2 где (1/r)1 и (1/r)2 – кривизны соответственно от непродолжительного действия кратковременных нагрузок и от продолжительного действия постоянных и длительных временных нагрузок - для участков с трещинами 1 1 1 1 1 1 . r r r 3 r 1 r 2 r 3 где: (1/r)1 – кривизна от непродолжительного действия всех нагрузок, на которые производят расчет по деформациям; (1/r)2 – кривизна от непродолжительного действия постоянных и длительных нагрузок; (1/r)3 – кривизна от продолжительного действия постоянных и длительных нагрузок. 2. В предварительно напряженных элементов полную кривизну определяют по формуле: • для участков без трещин в растянутой зоне: 1 1 1 1 r r 1 r 2 r 3 где (1/r)1 и (1/r)2 – кривизны соответственно от непродолжительного действия кратковременных нагрузок и от продолжительного действия постоянных и длительных нагрузок. (1/r)3 – кривизна (выгиб) от непродолжительного действия усилия предварительного обжатия P (т.е. при действии M = P eop). • для участков с трещинами 1 1 1 1 r r 1 r 2 r 3 где (1/r)1 – кривизна от непродолжительного действия всех нагрузок (включая усилие обжатия), на которые производят расчет по деформациям; (1/r)2 – кривизна от непродолжительного действия постоянных и длительных нагрузок (включая усилие обжатия); (1/r)3 – кривизна от продолжительного действия постоянных и длительных нагрузок (включая усилие обжатия). На участках элемента без трещин кривизну определяют как для сплошного приведенного сечения в стадии I напряженно-деформированного состояния: 1 M r Bred где Bred – жесткость приведенного сечения (при продолжительном действии нагрузки с учетом ползучести бетона). Bred Eb1 I red . Ired – момент инерции приведенного поперечного сечения, включающего в себя площадь поперечного сечения только сжатой зоны бетона и площади сечения сжатой и растянутой арматуры, умноженные на коэффициент приведения арматуры к бетону Eb1 – модуль деформации сжатого бетона при непродолжительном действии нагрузки Eb1 0.85 Eb при продолжительном действии нагрузки Eb Eb1 1 b,cr b,cr - коэффициент ползучести бетона На участках, где образуются нормальные трещины, элемент работает в стадии II. Общее деформированное состояние определяют через средние деформации бетона, средние деформации арматуры и для среднего положения нейтральной оси. 1 M r Eb,red I red Ired – момент инерции приведенного поперечного сечения относительно его центра тяжести. Определяется по общим правилам сопротивления упругих материалов. Учитывается площадь поперечного сечения только сжатой зоны бетона и площади сечения сжатой арматуры с коэффициентом приведения s1 и растянутой арматуры c коэффициентом приведения арматуры к бетону s2. I red I b I s s 2 I s s1 Ib, Is, I's - моменты инерции площадей сечения соответственно сжатой зоны бетона, растянутой и сжатой арматуры относительно центра тяжести приведенного без учета бетона растянутой зоны поперечного сечения. Высоту сжатой зоны бетона определяют из решения уравнения: Sb s 2 S s s1 S ' s где Sb, Ss и S’s – статические моменты соответственно сжатой зоны бетона, площадей растянутой и сжатой арматуры относительно нейтральной оси. Для прямоугольных тавровых и двутавровых сечений высоту сжатой зоны можно определить по формуле: hf a 2 z x h0 z 2 s s 2 s s1 f h 2 h 0 0 где z s s 2 s s1 f s As ; b h0 s As ; b h0 f bf b hf b h0 Eb,red – приведенный модуль деформации сжатого бетона, принимаемый равным: Eb,red где значение Rb, ser b1,red . равно: - при непродолжительном действии нагрузки b1,red 1510-4; - при продолжительном действии нагрузки b1,red принимается по таблице Влажность w b1,red при w > 75% 2410-4 при 75% w 40% 2810-4 при w < 40% 3410-4 Значения коэффициентов приведения для сжатой арматуры : s1 Для растянутой арматуры s2 Es ; Eb,red Es ; s Eb,red s – коэффициент, учитывающий неравномерное распределение относительных деформаций растянутой арматуры между трещинами. Можно определять эти коэффициенты приведения по упрощенным формулам: s2 s1 ; s s1 300 Rb, ser s1 560 - при продолжительном действии нагрузки и нормальной влажности Rb, ser окружающего воздуха (w = 40…75%); - при непродолжительном действии нагрузки; Для прямоугольных, тавровых и двутавровых элементов без предварительного напряжения можно проводить расчет по упрощенной формуле: - определяется по табл. 4.5 Пособия к СП 63.13330.2012 в зависимости от величин: - определяется по табл. 4.6 Пособия к СП 63.13330.2012 в зависимости от величин: Приведенное поперечное сечение (а) и схема напряженно деформированного состояния изгибаемого предварительно напряженного элемента с трещинами (б) при расчете его по деформациям 1 - центр тяжести арматуры растянутой зоны Для предварительно напряженных элементов полную кривизну определяют по формуле: 1 M P e0 p r D где М - изгибающий момент от внешней нагрузки; P и еор - усилие предварительного обжатия и его эксцентриситет относительно центра тяжести приведенного поперечного сечения элемента; D - изгибная жесткость приведенного поперечного сечения элемента, определяемая как для внецентренно сжатого усилием предварительного обжатия элемента с учетом изгибающего момента от внешней нагрузки. Полная кривизна (пособие к СП 63.13330.2018): 1 P r S red Eb,red где Sred – статический момент приведенного поперечного сечения относительно нейтральной оси Eb,red – приведенный модуль деформации сжатого бетона, который вычисляется как для элементов без предварительного напряжения. Высоту сжатой зоны x определяют из решения уравнения: I red M esp h0 x S red P где Ired – момент инерции приведенного поперечного сечения относительно его нейтральной оси, esp – расстояние от точки приложения усилия обжатия P до центра тяжести растянутой арматуры Для прямоугольных, тавровых и двутавровых элементов можно проводить расчет по упрощенной формуле при: hf 0.3 h и as 0.2 h 0 1 M r c b h03 Eb,red Коэффициент с определяется в зависимости от f, s2, es/h es M esp P As Asp 0.5 f ; b h0 hf h0 ; bf b hf Asp As s1 b h0 Расчет прогибов железобетонных элементов По формулам строительной механики значение прогиба от изгиба определяется по формуле: l 1 f M x dx r x 0 где – M x изгибающий момент в сечении x от действия единичной силы, приложенной в сечении, для которого определяется прогиб; (1/r)x – полная кривизна элемента в сечении x от внешней нагрузки, при которой определяют прогиб. Условие не наступления предельного состояния II-й группы по прогибом где - наибольший допускаемый нормами прогиб конструкции по СП 20.13330.2016, прил. Д. Порядок расчета: 1. Элемент разбивается на ряд участков. 2. В пределах участка изменение кривизны принимается линейным. 3. Определяется кривизна по их концам (с учетом наличия трещин). 4. Затем перемножается эпюра моментов и эпюра (1/r) по длине элемента. В этом случае прогиб в середине пролета будет определяться путем перемножения эпюр по формуле Верещагина. Тогда: n 1 2 1 l 1 1 1 1 f 6 i 3 n 2 2 12 n r sup,l r sup,r r c i 1 r i ,l r i ,r где (1/r)sup,l и (1/r)sup,r – кривизна соответственно на левой и правой опорах; (1/r)i,l и (1/r)i,r – кривизна элемента в симметрично расположенных сечениях i и i’, расположенных слева и справа от оси симметрии. (1/r)sup,с – кривизна в середине пролета; n – четное число участков разбиения пролета (не меньше 6); l – пролет элемента. Для свободно опертых и консольных элементов прогиб определяется по формуле 1 f S l2 r max (1/r) max - кривизна в сечении с наибольшим изгибающим моментом; S – коэффициент, зависящий от условий опирания. Для изгибаемых элементов при l/h < 10 необходимо учитывать влияние поперечных сил на прогиб. В этом случае прогиб будет равен сумме прогибов от изгиба и от сдвига fq. l f Qx x dx 0 Qx – поперечная сила в сечении от действия внешней нагрузки, при которой определяется прогиб. x – угол сдвига элемента в сечении от действия внешней нагрузки. Для элементов без трещин величина x определяется по формулам строительной механики: x G 1.5 Qx S red b I red Так как эпюра касательных напряжений по высоте сечения не постоянна, то более точно: 1.2 Qx x bG h При наличии трещин угловые перемещения увеличиваются: x 1.2 Qx b crc G b h b – коэффициент, учитывающий влияние ползучести бетона и принимаемый равным: • при длительном действии нагрузок: b = 1 + b,cr (табл. 4.4 Пособия к СП 63.13330.2012); • при непродолжительном действии нагрузки b = 1. crc – коэффициент, учитывающий влияние трещин не деформации сдвига: • на участках без трещин crc = 1; • на участках, где есть только наклонные трещины crc = 4.0; • на участках, где есть только нормальные или нормальные и наклонные трещины: crc 3 Eb I red 1 Mx r x Образование наклонных трещин проверяется по условию: Q 0.5 Rbt ,ser b h0